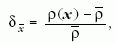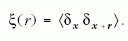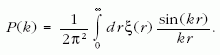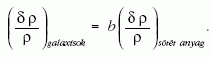Fizikai Szemle 2007/12. 385.o.
AZ UNIVERZUM SZERKEZETE
Csabai István, Purger Norbert, Dobos László
ELTE TTK, Komplex Rendszerek Fizikája Tanszék
Szalay Sándor, Budavári Tamás
The Johns Hopkins University,
Department of Physics and Astronomy, Baltimore, USA
A kozmikus mikrohullámú háttérsugárzás az Univerzumnak
az általunk jelenleg észlelhető legrégebbi állapotáról
ad számot. Az Univerzum akkori képe meglehetősen
homogénnek és izotrópnak tűnik, a relatív
fluktuációk nagyságrendje csupán 10-5 nagyságrendű.
Ezzel szemben a mai Világegyetemben hatalmas sűrűségkontrasztot
mutató struktúrákat látunk minden skálán:
bolygókat, csillagokat, galaxisokat, galaxishalmazokat
és szuperhalmazokat. Míg az intergalaktikus térben
kevesebb mint 1 hidrogénatom van köbméterenként,
addig például egy neutroncsillag tömegét 1018
kg/m3-re becsüljük, ami lokálisan 1045 mértékű sűrűségkülönbséget
jelent. Noha számos részlet még nem
világos, és néhány új, rejtélyes szereplő is megjelent a
színen, a különböző skálákon végzett, egyre szaporodó
észlelési eredményekre támaszkodva mindinkább tisztul
a kép, hogy hogyan jöttek létre a struktúrák, hogyan
alakult ki az Univerzum komplex szerkezete a kezdetben
szinte homogén ősállapotból.
Az Univerzum jelenleg legáltalánosabban elfogadott
modelljét a részecskefizikáéhoz hasonlóan „standard
modell”-nek nevezik. Mindjárt látni fogjuk, hogy olyan
szempontból nagyon találó a hasonló elnevezés, hogy
a modell nagyon kiváló egyezéseket mutat az összes
észleléssel, viszont számos olyan részlet van benne,
melynek elméleti alapjait, finoman szólva, nem teljesen
kielégítően értjük még. Az Univerzum fejlődésének históriáját
nagyon sokan, nagyon sok helyen elmondták
már, de azért, hogy az aktuális új eredmények is helyet
kaphassanak benne, valamint rávilágíthassunk a struktúrák
kialakulásával kapcsolatos mozzanatokra, tekintsük
át először nagyon röviden a történetet és az elméleti
hátteret, majd az észlelések tükrében vizsgáljunk meg
részletesebben bizonyos eseményeket.
Az Univerzum nagyon rövid története
Kezdetben volt az ősrobbanás. Ennek pontos mikéntjét
itt nem tárgyaljuk részletesen, számunkra most csupán
az a fontos, hogy olyan kvantumfluktuációk játszanak
benne szerepet, melyek már ekkor, nagyon kis mértékben
ugyan, de inhomogenitást hoznak be a térbeli eloszlásba.
A további folyamatok ugyanis nagyrészt ezeket
a térbeli fluktuációkat módosítják: ha minden egzaktul
homogén lett volna kezdetben, akkor nem kapnánk
meg a jelenleg látható struktúrákat. Az ősrobbanást
követő nagyon gyors kitágulással járó inflációs
fázis szinte teljesen homogénné és izotróppá teszi az
Univerzumot, csupán apró, nagyjából skálafüggetlen
Gauss-fluktuációk maradnak meg. Fontos megjegyezni,
hogy ezeknek a fluktuációknak a nagysága és eloszlása
nagyon érzékenyen befolyásolja, hogy később, például
a gravitáció hatására mikor és mekkora anyagcsomók
állhatnak össze, lesznek-e csillagok és galaxisok, mekkora
lesz azok tipikus tömege. Az infláció az Univerzum
10-32 másodperces korára lezajlik, a táguló és hűlő
világban kialakulnak a hadronok és leptonok nagyjából
a 3. perc végére (1. ábra).
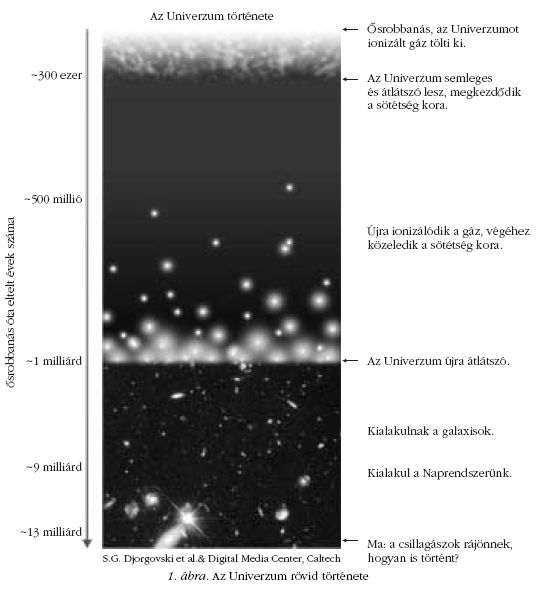 A következő szakaszban a struktúraképződés szempontjából
újabb, fontos jelenségek játszódnak le. Az
Univerzum ekkor forró, táguló ionizált gáznak tekinthető.
A magas hőmérséklet miatt a fotonok dominálják az
eseményeket egészen az Univerzum nagyjából 380 ezer
éves koráig. A fotonoknak nagyon rövid a szabad úthosszuk,
nagyon gyakran ütköznek. A rendszer állapotegyenletét és dinamikáját
megvizsgálva kiderül, hogy
ebben a plazmában olyan rezgések
indulnak be, amelyek
leginkább akusztikus rezgésekhez
hasonlatosak, és ezért
hanghullámoknak nevezik
őket. Ezek azért fontosak,
mert, mint ahogy látni fogjuk,
a hanghullámok sűrűségfluktuációkat
okoznak, és ezek
nyoma még a jelenlegi galaxiseloszlásban
is kimutatható.
Miután a plazma annyira lehűlt
és kiritkult, hogy kialakulhattak
az első atomok, és a fotonok
szabadon repülhettek,
egyre inkább a gravitáció vette
át a struktúra formálásában a
vezénylést. A kezdeti kis sűrűségfluktuációk
a gravitáció
vonzása alatt egyre növekedtek.
A jelenlegi, úgynevezett
hideg sötét anyag modell
(Cold Dark Matter, CDM) szerint
a sötét anyag gravitációs
völgyeket hozott létre, és az
ebbe belezuhanó hidrogéngáz
addig sűrűsödött, míg begyulladtak
az első csillagok, és/vagy az első aktív galaxismagok.
Erről a "sötét” korszakról
jelenlegi műszereinkkel nem
tudunk sokat megállapítani a
semleges hidrogéngáz elnyelése miatt. A csillagok ultraibolya
fénye később ionizálta a semleges hidrogént,
valamint a szupernóva-robbanások legyártották a nehezebb
elemeket is. A kisebb galaxiskezdemények összekapcsolódtak,
és a fokozatos összeolvadások során kialakultak
a ma is látható galaxisok.
A következő szakaszban a struktúraképződés szempontjából
újabb, fontos jelenségek játszódnak le. Az
Univerzum ekkor forró, táguló ionizált gáznak tekinthető.
A magas hőmérséklet miatt a fotonok dominálják az
eseményeket egészen az Univerzum nagyjából 380 ezer
éves koráig. A fotonoknak nagyon rövid a szabad úthosszuk,
nagyon gyakran ütköznek. A rendszer állapotegyenletét és dinamikáját
megvizsgálva kiderül, hogy
ebben a plazmában olyan rezgések
indulnak be, amelyek
leginkább akusztikus rezgésekhez
hasonlatosak, és ezért
hanghullámoknak nevezik
őket. Ezek azért fontosak,
mert, mint ahogy látni fogjuk,
a hanghullámok sűrűségfluktuációkat
okoznak, és ezek
nyoma még a jelenlegi galaxiseloszlásban
is kimutatható.
Miután a plazma annyira lehűlt
és kiritkult, hogy kialakulhattak
az első atomok, és a fotonok
szabadon repülhettek,
egyre inkább a gravitáció vette
át a struktúra formálásában a
vezénylést. A kezdeti kis sűrűségfluktuációk
a gravitáció
vonzása alatt egyre növekedtek.
A jelenlegi, úgynevezett
hideg sötét anyag modell
(Cold Dark Matter, CDM) szerint
a sötét anyag gravitációs
völgyeket hozott létre, és az
ebbe belezuhanó hidrogéngáz
addig sűrűsödött, míg begyulladtak
az első csillagok, és/vagy az első aktív galaxismagok.
Erről a "sötét” korszakról
jelenlegi műszereinkkel nem
tudunk sokat megállapítani a
semleges hidrogéngáz elnyelése miatt. A csillagok ultraibolya
fénye később ionizálta a semleges hidrogént,
valamint a szupernóva-robbanások legyártották a nehezebb
elemeket is. A kisebb galaxiskezdemények összekapcsolódtak,
és a fokozatos összeolvadások során kialakultak
a ma is látható galaxisok.
A modell és paraméterei
A Világegyetem tágulását legegyszerűbb közelítésben
a Friedman-egyenletek írják le:
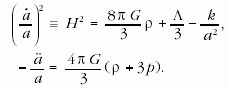
Az első egyenlet a tágulás mikéntjét mutatja, a második
pedig az állapotegyenlet. A képletekben a jelöli a
skálafaktort, ami a relatív tágulás mértékét fejezi ki, a
felülpontozás szokott módon az időderiváltat jelöli.
Az 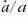 arány, a Hubble-paraméter megmondja, hogy
adott távolságon lévő két pont milyen látszólagos
sebességgel távolodik egymástól. Ezt a távolodást
mérésekkel is ki lehet mutatni, és a Hubble-törvény
értelmében egy tőlünk D távolságra lévő galaxis látszó
radiális távolodási sebessége v = H · D. Itt jegyezzük
meg, hogy sem a távolságot, sem pedig a távolodási
sebességet nem lehet közvetlenül mérni, ezek
észlelése volt az elmúlt évtizedek egyik nagy kihívása
a kísérleti kozmológiában. A jobb oldalon az első tag
az anyag hatását írja le, G a gravitációs állandó, ρ
pedig az anyagsűrűség, magában foglalva a barionikus
anyagot, a fotonokat és a sötét anyagot is. Gyakran
a sűrűséget nem közvetlenül, hanem a
arány, a Hubble-paraméter megmondja, hogy
adott távolságon lévő két pont milyen látszólagos
sebességgel távolodik egymástól. Ezt a távolodást
mérésekkel is ki lehet mutatni, és a Hubble-törvény
értelmében egy tőlünk D távolságra lévő galaxis látszó
radiális távolodási sebessége v = H · D. Itt jegyezzük
meg, hogy sem a távolságot, sem pedig a távolodási
sebességet nem lehet közvetlenül mérni, ezek
észlelése volt az elmúlt évtizedek egyik nagy kihívása
a kísérleti kozmológiában. A jobb oldalon az első tag
az anyag hatását írja le, G a gravitációs állandó, ρ
pedig az anyagsűrűség, magában foglalva a barionikus
anyagot, a fotonokat és a sötét anyagot is. Gyakran
a sűrűséget nem közvetlenül, hanem a
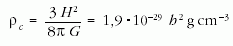
kritikus sűrűséggel normálva használjuk:
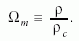
A kritikus sűrűséget az jelöli ki, hogy ennél nagyobb
sűrűségekre (0 görbület és kozmológiai konstans mellett)
az Univerzum végül összeesik, ennél nagyobb
értékekre pedig a végtelenségig folyamatosan tágul.
Az első egyenletben még két tagról nem szóltunk: Λ
az egyelőre titokzatos sötét energiát, vagy kozmológiai
konstanst írja le, k pedig az euklideszitől esetlegesen
eltérő tér görbületét. A mérések eddigi tanúsága szerint
a tér lapos, tehát ez utóbbi faktor kiesik az egyenletből.
Mint ahogyan az anyagsűrűségnél tettük, hasonlóan
normált, dimenziótlan változókra térhetünk át a kozmológiai
konstans és a görbület esetében is. Így a tágulást
kifejező egyenletből az alábbi formát kaphatjuk:
1 = Ω0 = Ωb + Ωd
+ Ωr + ΩΛ + Ωk .
Ez egyfajta mérlegegyenlet, amely a különböző összetevők
arányát írja le. Jelenlegi legjobb tudásunk szerint az
Univerzum euklideszi, vagyis Ωk, valamint a sugárzás
(fotonok) járuléka jelenleg csekély, tehát Ωr is 0. Csupán
egy évtizede gyűlnek az egyre biztosabb jelek, hogy a
kozmológiai konstans értéke nem nulla, sőt elég jelentős
ΩΛ = 0,74, de, sajnos a sötét energiáról ennél több információ
nem igen áll rendelkezésünkre. A fennmaradó
0,26-on osztozik a sötét és „világító” anyag. Ebből is
jelentős hányad (Ωd = 0,22) a sötét anyagra esik, amelynek
természetéről szintén keveset tudunk, annyi bizonyos,
hogy csak gravitációs hatását tapasztaltuk eddig.
A teljes mérlegből csekély 4% marad a minket és bolygónkat
alkotó, valamint főként a csillagokban és szabad
hidrogén- és héliumgáz formájában jelen lévő barionikus
anyagra (Ωb = 0,04).
A második egyenletben p a nyomást jelöli. Attól
függően, hogy az Univerzum különböző korszakaiban
milyen anyagféleség dominálta a világot, a sűrűség
és a nyomás között különböző relációk álltak
fenn. Ezek a különböző állapotegyenletek persze más
és más tágulási történeteket eredményeznek. Nézzük
meg a tiszta egykomponensű eseteket.
Kezdetben, amikor a vákuum energiája dominálta
az Univerzumot, az állapotegyenletbe a
p = - ρ
alakot beírva exponenciálisan gyorsuló felfúvódást
kapunk:
a(t) ~ exp (Ht)
Később a forró plazma állapotban a fotonok játszották
a főszerepet. Tiszta fotongázra
p = ρ /3
,
ami az idő négyzetgyökével arányos, jelentősen lassabb
tágulást eredményez:
a(t ) ~ t½.
Végül jelenlegi, ritka anyag dominálta Univerzumunkban
a nyomás zérus,
p = 0,
amely összefüggés, a gravitáció hatását figyelembe
véve, egy más kitevőjű hatvánnyal való tágulást eredményez:
a(t ) ~t 2/3.
Itt jegyezzük meg, hogy a kozmológiai konstans
nullától különböző értékének alig egy évtizede történt
kísérleti megalapozása óta számosan úgy kalkulálnak,
hogy a gyorsulva táguló Világegyetemben az anyag
dominanciája ismét a vákuumnak adhatja át a stafétabotot,
mintegy széttépve ezzel a Mindenséget.
A fenti egyenletek persze csak nagy vonalakban adják
meg a fejlődést, számos részletet kell még hozzátenni,
hogy a kép kisebb skálákon is teljes legyen, és a
struktúrák kialakulását részletesen megérthessük. Ilyenek
a nukleoszintézis, a csillag- és galaxiskeletkezés
szabályai, vagy például a szupernóva-robbanások lökéshullámainak
hatása. Noha nagy utat kell még megtenni,
de eme jelenségkörök részletei szinte napról
napra tisztulnak, és egyre nyilvánvalóbb, hogy a teljes
megértéshez sokkal komplexebb képet kell kialakítani.
A szerkezet leírása
Az Univerzum nagy léptékű (galaxisklaszterek mérete
fölötti) szerkezetét statisztikai módszerekkel írjuk le.
Ehhez az anyagsűrűségnek az átlagostól 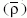 való
eltérését, azaz fluktuációit vizsgáljuk:
való
eltérését, azaz fluktuációit vizsgáljuk:
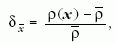
A fluktuációknak vizsgálhatjuk a korrelációit, például
a leggyakrabban használt kétpont-korrelációs függvény
segítségével:
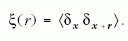
A korrelációs függvény azt méri, hogy a tér két, r
távolságban levő pontjabeli relatívsűrűség-eltérés
mennyire hasonlít egymáshoz. Ha nincsenek korrelációk,
akkor ez a függvény lapos, ha pedig, például,
valamilyen karakterisztikus méret fordul elő, akkor az
annak megfelelő értékeknél csúcsokat kapunk. Matematikailag
ezzel ekvivalens, ha a korrelációs függvény
Fourier-transzformáltját, a teljesítménysűrűségspektrumot
vesszük:
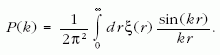
Noha matematikailag ekvivalensek, technikai okok
miatt, valamint azért hogy a mérési hibákat korrektül
kezelhessük, a méréstől függően egyik vagy másik
statisztika használata célszerűbb.
Mivel a Friedman-egyenletek a kisebb skálák nemlineáris
jelenségeit nem írják le, az általánosan elfogadott
nézet szerint azokat leginkább a csak gravitációsan
kölcsönható sötét anyag evolúciójának kiszámítására
használhatjuk fel. A galaxisok "világító” anyagának
eloszlása nem követi pontosan ezt az eloszlást,
hanem a sötét anyag által kialakított gravitációs völgyek
legmélyén gyullad csak be. Ez az úgynevezett
"biasing” jelenség, amelyet a legegyszerűbb, lineáris
esetben egyetlen b faktorral jellemezhetünk:
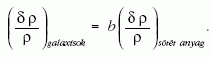
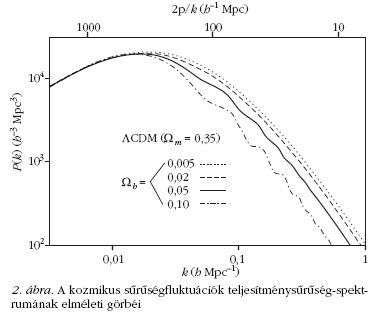
Nézzük meg konkrétan, hogyan néz ki a teljesítménysűrűség-spektrum
a hullámszám (illetve a felső
skálán a hullámhossz) függvényében (2. ábra).
A hullámszám 1/hosszúság mértékegységű, a hoszszúságot
megaparsecben (Mpc) mérjük, ahol 1 parsec
= 3,26 fényév vagy nagyjából 3 · 106 méter. A mértékegység
előtt lévő h faktor a Hubble-állandó dimenziótlan,
normált változata (H = h · [100 km/ s / Mpc]),
és azért szokott szerepelni a kifejezésekben és ábrákon,
mivel pontos értéke, (az eddigi mérések alapján
0,72) sokáig bizonytalan volt, de tőle függően minden
méret átskálázódik.
Mit is látunk az ábrán? Az egyes görbék egy olyan
sík Univerzum spektrumát ábrázolják, ahol a sötét és
barionikus anyag (Ωm) együttes aránya 0,35, és ebből
a görbéken felülről lefelé haladva rendben 0,005,
0,02, 0,05, illetve 0,1 a barionikus anyag mennyisége.
Láthatjuk hogy az arány változtatásával más görbéket
kapunk. A jelenlegi kozmológiai vizsgálatok éppen
erről szólnak: számoljuk ki az Univerzum modelljeit
különböző paraméterekkel, és rajzoljuk fel valamilyen
mérhető mennyiség vagy statisztika, mint például a
fent mutatott sűrűségfluktuáció-spektrum görbéjét.
Végezzünk méréseket, és vessük össze, hogy mely
modell, milyen paraméterek mellett illeszkedik legjobban
az észlelésekhez. Így egyre nagyobb statisztikával,
egyre több irányú és pontosabb mérésekkel,
egyre jobban rögzíthetjük modellünket és paramétereit.
Pár éve ez még csak álom volt, de a jelenlegi
nagy skálás mérések a nem olyan régen még szinte
csak filozofikus kérdéseket tárgyaló kozmológiát precíziós
kísérleti tudománnyá alakították.
Nagyszabású szimulációk
Ahhoz tehát, hogy feltárjuk a kozmológiai struktúraképződés
részleteit, lehetőleg az ég minél nagyobb
területéről, minél több adatot kell begyűjteni. Szerencsénkre
a fotonok sebessége véges, így nem csupán
az Univerzum jelenét, hanem a múltját is direkt
módon tanulmányozhatjuk, hiszen vannak olyan fotonok,
amelyek már milliárd évekkel ezelőtt indultak el
útjukra, de csak most érnek detektorainkhoz. Ha elég
érzékeny műszerrel tekintünk az égre, akkor optikai
és ahhoz közeli tartományokban visszatekinthetünk
egészen addig a korszakig, amikor az Univerzum csupán
pár százmillió éves volt. Itt, mint ahogy az 1. ábrán
láthatjuk, elérjük a reionizáció előtti "sötétség
korát”, amikor is az összefüggő neutrális hidrogénfelhő
nem engedi át a fényt. A hidrogéngázról az iskolában
azt tanuljuk ugyan, hogy színtelen, átlátszó gáz,
de jól ismert, hogy az ultraibolya-tartományban lévő
fotonokat elnyeli (gerjesztési és ionizációs vonalak).
Mivel a fény vöröseltolódást szenved miközben felénk
tart, ezek az elnyelési vonalak végigvonulnak a
teljes látható színképen, és mindent nullával tesznek
egyenlővé. Sokkal távolabbra egyébként se látnánk,
ez a kor azért is sötét, mert nincs amit láthatnánk.
Ugyanis nem túl sokkal a reionizáció előtt gyulladtak
be az első csillagok és esetleg aktív galaxismagok
(létrehozván magát a reionizációt is), amelyek egyáltalán
fényt bocsátanak ki.
Szerencsénkre azonban van még egy csecsemőkori
képünk is az Univerzumról, abból az időből, amikor
nagyjából 380 ezer éves volt. Ennek megértéséhez ismét
a történelmi bevezetőre és az 1. ábrára utalunk
vissza. Amikor a korai Univerzum forró plazmája a tágulás
során egyre hűlt, elérkezett az a pillanat, amikor a
fotonok szabad úthossza végtelenre nőtt. Az akkori, néhány
ezer fokos plazmauniverzum hőmérsékleti sugárzásának
fotonjai tehát attól kezdve repülnek felénk, de
mivel a tér azóta jelentősen kitágult, ezek a fotonok
annyira megnyúltak, hogy átkerültek a mikrohullámú
tartományba, és mintegy 2,7 kelvin a karakterisztikus
hőmérsékletük. A plazmakorszak szimulációja viszonylag
egyszerű, a kezdeti, véletlenszerű kvantumfluktuációkat
kell a tágulás során nyomon követni, és hozzákombinálni
azokat az akusztikus sűrűsödési hullámokat,
amelyeket a forró plazma rezgése keltett. Természetesen,
ha más például a barionikus és sötét anyag
aránya, akkor hasonlóan ahhoz, mint ahogy a különböző
fémekből öntött harangok más és más hangszínen
csengenek, az Univerzum "szférájának zenéje”, vagyis a
fluktuációspektrum is más és más lesz. Wayne Hunak
a Chicagói Egyetemen lévő weboldalán
(
http://background.uchicago.edu/~whu/metaanim.html)
például különböző animációkat láthatunk arra vonatkozóan,
hogy miként változik a fluktuációk spektruma, ha
változtatjuk a barionikus anyag arányát vagy a többi
kozmológiai paramétert. A 2. ábra ilyen jellegű görbékből
mutat néhányat.
Valamivel komplikáltabb az anyag csomósodásának
végigkövetése, melyet a végtelen hatótávolságú
gravitáció hatása hoz létre. Egy ilyen N-test szimulációban
az anyagnak kis darabjait, "részecskéit”
vesszük és számoljuk ki mozgásukat a többi részecske
gravitációs terében. Ha nagy skálán nagyjából homogén
az anyag eloszlása, akkor egy adott ponttól R
távolságra lévő gömbhéjban foglalt anyag összes tömege
R2-tel arányos. Mivel a gravitációs erő éppen
1/R2-tel cseng le, a közeli és távoli pontoknak a
hatása azonos nagyságrendű, így a mozgásegyenletek
kiszámolásakor minden pont minden másik ponttal
való kölcsönhatását figyelni kell, azaz N részecske
esetében N × N számítást kell elvégezni minden időlépésben.
Ahhoz hogy a szimuláció kellően pontos
legyen, a Virgo Consortium néven ismert nemzetközi
kutatócsoport Millennium Projektje
(
http://www.mpa-garching.mpg.de/galform/virgo/millennium/)
például 10 milliárd "részecske” pályáját követte egy 2
milliárd fényév oldalhosszúságú kockában, több mint
10 milliárd éven át. Nem csoda, hogy a szimuláció
még számos numerikus programozási trükk felhasználásával
is 30 napig futott 1500 processzoron, és
több mint 25 terabájtnyi adatot eredményezett (3.
ábra). A szimuláció igazából a sötét anyag viselkedését
követte, és a méretfelbontás alsó határa a galaxishalmazok
tartományába esik.
Lehet, hogy csupán azért, mert keveset tudunk róla,
a sötét anyag viselkedését egyszerűbbnek gondoljuk,
mivel csak gravitációsan hat kölcsön. A sötét anyag
szimuláció által így kialakított gravitációs völgyek legmélyebb
részein gondoljuk, hogy a hidrogéngáz annyira
összesűrűsödhetett, hogy begyulladhattak a csillagok,
kialakulhattak a galaxisok. A galaxiskeletkezés
pontos mikéntjének megértése még időbe telik, hiszen
olyan komplex jelenségek tarkítják, mint a csillagokban
lezajló magfizikai folyamatok, a szupernóva-robbanások
lökéshullámaival szétszórt nehéz elemek turbulens
keveredése, vagy például a galaxisok aktív magjában
lévő fekete lyukakba áramló anyag dinamikája.

Kozmikus távolságok
Mielőtt rátérünk a kozmikus struktúra észlelésének két
kísérleti pillérére, hadd szóljunk röviden a harmadikról,
amely közvetve ugyan nem a struktúrát vizsgálja, de azzal,
hogy a kozmikus távolságskálát kalibrálja, a másik
két vizsgálat eredményeit is nagyban befolyásolja. Az
égi hosszúsági és szélességi koordinátákat ugyanis nagyon
könnyen mérhetjük, viszont egy galaxisnak tőlünk
vett távolságáról nehéz információhoz jutni. Nincs
is igazán más módszer rá, mint egyre nagyobb skálákon
használható módszerek összeillesztésével egy úgynevezett
távolságlétrát bekalibrálni. A kalibráció első
lépcsőfoka a parallaxis. A közeli csillagok ugyanis
olyan távolságokon vannak, amelyek gondos vizsgálatokkal
összemérhetőek a földpálya átmérőjével. Ha
ugyanis ugyanarra a csillagra a Föld Nap körüli pályájának
két átellenes pontjáról nézünk rá, akkor egy nagy
egyenlő szárú háromszöget feszítünk ki, melynek alapja
a földpálya átmérője. A háromszög magassága az
alaphoz képest nagyon nagy, s így a vele szembe levő
szög nagyon kicsi. Ha távcsövünkkel azért le tudjuk
mérni ezt a pici szögeltérést, akkor ki tudjuk számítani
a csillag távolságát. Sajnos ez csak a legközelebbi csillagokra
működik, viszont közöttük vannak érdekes változó
csillagok, a cefeidák, amelyek fényének változási
periódusa kapcsolatban áll abszolút fényességükkel.
Ha így abszolút fényességüket bekalibráltuk, nyert
ügyünk van, hiszen a fényintenzitás 1/távolság²-es
csökkenése alapján tetszőleges helyen meg tudjuk határozni
távolságukat. Persze, praktikusan nem tetszőleges
távolságban, hiszen egy adott távolságon túl már
túl haloványak távcsöveink számára. A cefeidák távoli
rokonai a szupernóvák, különösen az Ia típusúak szintén
standard gyertyaként használhatók, még nagyobb
távolságokon is, hiszen robbanásukkor fényük akár
egy galaxis milliárd csillagát is képes túlragyogni. Segítségükkel
tehát kiléphetünk a galaktikus skálákra. Sajnos
egy-egy galaxisban átlagosan csak 100 évente láthatunk
ilyen felvillanást, a nagyon távoliakban pedig
nem igazán észlelhetőek, így mindegyik galaxist nem
tudjuk ily módon bekalibrálni. A szupernóvák észlelése
és a távolságskála rögzítése a kozmológiai modell tisztázása
szempontjából nagyon kritikus, ezért számos felmérést
indítottak a közelmúltban, hogy minél több és
minél távolabbi galaxishoz szerezzünk be adatokat. A
kérdés fontossága persze mindig vonzza a kritikus hangokat
is, hiszen ha az adatokat rosszul kalibráljuk, például
a galaktikus por miatt, vagy nem megbízhatóak a
szupernóvamodelljeink, akkor a jelenlegi kozmológiai
modellek érvényessége kétségbe vonható. A vitákat itt
is, reméljük mihamarabb, az adatok gyarapodása fogja
eldönteni.
Ha elfogadjuk a Hubble-törvényt, és a cefeidák
valamint a szupernóvák segítségével bekalibráljuk,
akkor nagyobb skálákon a vöröseltolódás szolgálhat a
távolság analógiájának. A vöröseltolódás a galaxisok
látszó radiális távolodásának eredménye, és a spektrumvonalak
vörös tartomány felé eltolódásában jelentkezik.
Ennek pontos méréséhez spektrumokat
kell felvenni, ami nagyon időigényes mérés. A majd
később tárgyalt SDSS például észlelési idejének 80%-
ban a maradék 20%-ban lefényképezett galaxisok csupán
1%-ának tudja a vöröseltolódását megmérni. Számos
nemzetközi csoporttal együtt kollégáimmal és
diákjaimmal sokat dolgoztunk azon a kérdésen, hogy
pusztán a fényképekből nyerhető fotometriai információ
alapján hogyan lehet a vöröseltolódást minél
pontosabban megbecsülni.
Nagyszabású észlelések
A kozmikus távolságokról szóló kitérő előtt említett,
különböző korokat leíró szimulációkat kell tehát összevetnünk
az észlelésekkel, hogy modelljeink helyességéről
meggyőződhessünk, illetve azok paramétereit
meghatározhassuk. Az észleléseknek hasonlóan nagy
skálát kell átfogniuk, és persze még nagyobb anyagi és
időbeli ráfordítást igényelnek a kutatóktól, mint a szimulációk.
Szerencsére a mikroelektronika és a technológia
fejlődése lehetővé tette, hogy az elmúlt évtizedben
számos nagyszabású felmérés végrehajtására alkalmas
eszközt hozzanak létre a kutatók. Az egyik felmérés,
amely egyik sarokköve a modern kísérleti kozmológiának,
a kozmikus háttérsugárzás detektálására alkotott
COBE és WMAP műholdakon nyugszik. Magának a
kozmikus mikrohullámú háttérnek felfedezéséért Arno
A. Penzias és Robert W. Wilson 1978-ban kaptak Nobel-
díjat. John C. Mather és George F. Smoot pedig
2006-ban azért kapták meg ezen elismerést, mert a fenti
műszerekkel ki tudták mutatni a kozmológiai modellek
által előrejelzett 10-5 nagyságrendű fluktuációkat a homogén
háttérhez képest. Ez nem volt könnyű dolog, hiszen
a fent említett nagyságrend szemléletesen azt jelenti,
hogy ha a sűrűségfluktuációkat kidomborodásoknak
tekintenénk egy gömb felszínén, akkor egy biliárdgolyó
tükörfényes felszínén kell tizedmikronnál kisebb
egyenetlenségeket feltérképezni, és korrelációit meghatározni.
A földi atmoszféra és rádiózavarok elkerülése
érdekében műholdról zajlottak a mérések, és az
égen végigpásztázva két-két pont hőmérsékletkülönbségét
mérték. A kapott eredményeket még korrigálni
kellett a galaxis és ismert extragalaktikus források zavaró
hatásainak kiküszöbölésére, de végül 1992-ben elkészült
a COBE nagyjából 7 fok felbontású, majd 2003-tól
egyre több adattal a WMAP pár tized fok felbontású térképe
(4. ábra).
Természetesen nem a konkrét térképet lehet összevetni
a szimulációkkal, hiszen ennek pontos képét
nagyban befolyásolja a kezdeti véletlen fluktuációk elrendeződése,
hanem a fent már említett korrelációs
függvényeket vagy fluktuációspektrumokat kell összevetni.
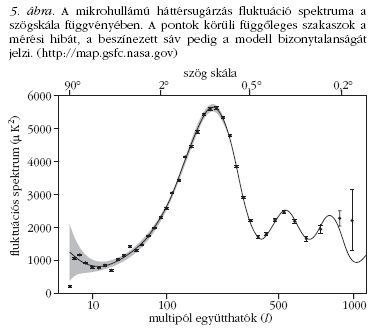
Mivel egy gömb felületét látjuk, célszerű a gömbfüggvények
szerint kifejteni a fluktuációkat, kezdve a
lassan változó hosszú hullámúaktól a nagyobb frekvenciás
rövid hullámúakig. Az észleléseknél minden skálán
ki tudjuk számolni a zajból és a műszer tökéletlenségéből
adódó hibákat is.

Az 5. ábráról leolvashatjuk, hogy a becsült mérési
hibák rendkívül kicsik, és a legjobban illeszkedő modell
jóslatát szinte minden skálán nagyon jól követi.
Megjegyezzük, hogy a legnagyobb szögskálákhoz
tartozó egyetlen kilógó pont szignifikanciája nagy
vihart kavart. Vannak, akik nagy jelentőséget tulajdonítanak
ennek, illetve a különböző multipólmódusok
fázisai egybeesésének, és a modellek alaposabb revízióját
javasolják. A többség inkább kivárja, amíg a
hamarosan üzembe állítandó, még precízebb Planck
műhold több adatot gyűjt be. Mindenesetre az ábrán
jól látszik, hogy a modellek által jósolt úgynevezett
akusztikus csúcsok létét a mérések kiválóan igazolják,
és a mérési pontosság határain belül az első két csúcs
pontosan illeszthető, szűk határok közé szorítva bizonyos
kozmológiai paraméterek értékeit.
Láttuk tehát az Univerzum csecsemőkori képét. Ha
modelljeink jók, akkor azt is pontosan vissza kell adniuk,
hogy az "ifjú”, majd a mai Univerzum hogyan
néz ki. Ehhez a galaxisok nagy léptékű eloszlását kell
megvizsgálni minél nagyobb vöröseltolódás-tartományban.
Az ég felületén nagy tartomány azért kell,
hogy a fluktuációspektrumnak minél nagyobb részéhez
illeszthessük modelljeinket, a mélyebb vöröseltolódások
pedig az említett Hubble-törvény értelmében
nagyobb távolságokat jelentenek, ahonnan a fény
hosszú idő alatt ér ide, vagyis távolabbi galaxisokat
észlelve az időskálát tágíthatjuk. Persze, ez a két követelmény
kompromisszumokra készteti az észlelő
csillagászokat. Ha felnézünk az égre, a népdalok tanúsága
szerint ragyognak a csillagok. Őszintébben
fogalmazva inkább pislákolnak, a galaxisok pedig
még szerényebben küldenek felénk néha-néha egy
pár kóbor fotont. Az észlelési idő (nem is beszélve a
pályázatok és doktori terminusok idejéről) viszont
véges, és ha műszerünk adott számú foton észlelésére
képes, akkor választhatunk, hogy egy kis területről
készítünk mélyebb felvételt, vagy pedig a teljes égboltról
egy sekélyebbet. Annak következtében, hogy
a csillagászok az eddig használt fotolemezekről a 90-es
évek közepétől kezdtek áttérni a CCD-eszközökre, a
vizsgálható térfogat szerencsére fokozatosan kitágul.
Az újfajta nagy skálás és viszonylag mély felmérések
prototípusa a Sloan Digital Sky Survey
(SDSS, http://www.sdss.org,
illetve magyarul http://skyserver.elte.hu).
Ezen a projekten a cikk egyik szerzője és diákjai (Győry
Zsuzsanna, Purger Norbert, Dobos László ) jó ideje dolgoznak,
de számos más magyar kutató, mint a tervezésben
és adatfeldolgozásban kulcsszerepet játszó Szalay
Sándor és volt diákjai (Budavári Tamás, Szokoly Gyula,
Szapudi István ) is hozzájárultak sikeréhez.

Az SDSS távcsöve egy földi távcső, 2,5 méteres tükörátmérőjével
a jelenlegi távcsövek középmezőnyétől
is lemarad. Különlegessége abban áll, hogy működését
több éven át teljes mértékben erre a projektre koncentrálták,
és két, a maga nemében és idejében egyedülálló
műszer helyezhető különlegesen nagy látószögű torzítatlan
fókuszsíkjába. Az egyik műszer, egy összesen
120 megapixeles kamera (6. ábra), amely az optikai
tartomány 5 sávjában készít felvételeket az égboltról.
Tervezésekor, illetve gyártásakor a 90-es évek végén ez
az egy távcső tartalmazta az összes csillagászati CCD-pixelek
nagyobbik hányadát. Ha arra még kell is egykét
évet várni, hogy mindannyiunk mobiltelefonjának
kamerája elérje ezt a felbontást, azért ma már számos
hasonló kaliberű csillagászati kamera áll rendelkezésre,
és hamarosan üzembe áll a Pan-Starrs projekt 1,4 gigapixeles
kamerája, amely az SDSS 5 éves munkáját alig
egy hét alatt lesz képes elvégezni.
Érdekességként jegyezzük meg, hogy a távcső, részben
azért, hogy a követő mechanikával spórolhassanak,
részben pedig azért, hogy a CCD-k kiolvasási holtidejétől
megszabaduljanak, úgynevezett "drift scan”
üzemmódban dolgozik. Ez azt jelenti, hogy miközben a
Föld forgása következtében az ég egy szelete végigpásztázza
az érzékelőt, ugyanebben az ütemben léptetik
a CCD-ből kifelé az adatokat. Így egy pontszerű forrás
képe egy CCD-oszlopon végighaladva integrálódik
ki, kiátlagolva az egyes pixelek különbségéből adódó
esetleges hibákat is, és megtakarítva a kiolvasási holtidőt.
Persze, ha mozgó objektumokat (pl. aszteroida)
fényképezünk, akkor , mivel a különböző színszűrők
időben követik egymást, azok színes gyöngysorként jelennek
meg a kombinált színes képeken.

A fotometria, vagyis a színes képek mellett a távcső
színképeket, spektrumokat is vesz fel. Hagyományosan
egy távcső egyszerre egy-két objektumról tudott
csak spektrumot készíteni, és mivel a fényt a hullámhossz
szerint szét kell szórni, nagyon sokáig kell exponálni,
hogy a zajból jól kiemelkedő jelet kapjunk.
Így olyan galaxis, amelyről teljes spektrum, így vöröseltolódás,
és a Hubble-törvény révén távolságinformáció
is rendelkezésre állt, az SDSS előtti időkben csupán
pár ezer volt. Az SDSS távcsövébe egy speciális
spektroszkóp került, amely a fókuszsíkba helyezett
üvegszálak által elvezetve, egyszerre 640 színképet
tudott felvenni. A fenti műszerek tették lehetővé,
hogy az SDSS működésének nagyjából 5 éve alatt
mintegy 150 millió galaxis és ugyanennyi csillag képét
készítse el, és közülük közel 1 milliónak a spektrumát
is felvegye. Az eredmény tehát egy több mint 1 milliószor
1 millió pixeles, 5 színben készült kép, és az objektumok
nagyjából 1 százalékának 3 dimenziós pozíciója.
Mindezen adatok nyilvánosak, sőt a több mint 3
terabájtnyi adat, mely hatékony kezelésének bonyodalmai
külön kihívást jelentenek, magyarországi szerverről
is elérhető.
Habár az 7. ábra nem tudja visszaadni a 3 dimenziót,
egyből láthatjuk, hogy a galaxisok eloszlása nem
homogén, sőt, örömmel fedezhetjük fel, hogy a hálószerű
szövedék struktúrája hasonló a Millennium-szimulációban
kapott eloszlásokhoz. A kozmikus mikrohullámú
háttér csekély 10-5-es fluktuációit a gravitáció
vonzó hatása galaxishalmaz méretű skálákon kétszeres
relatív sűrűségeltérésekké növelte, amelyet a korábban
említett bias tovább növel. Természetesen nem csak
szemünkre kell hagyatkozni, amikor a galaxiseloszlást
össze akarjuk hasonlítani a modellekkel. Erre is kiszámolható
a fluktuációspektrum, hasonlóan, mint ahogy
a kozmikus mikrohullámú háttér esetében tettük. A két
spektrumnak nem direkt módon kell illeszkedni, hiszen
az Univerzum más korszakáról készültek a felvételek,
de az akusztikus csúcsok jelenlétére itt is számítunk,
illetve az illesztett modellparamétereknek az ott kapottakkal
konzisztensnek kell lenniük.
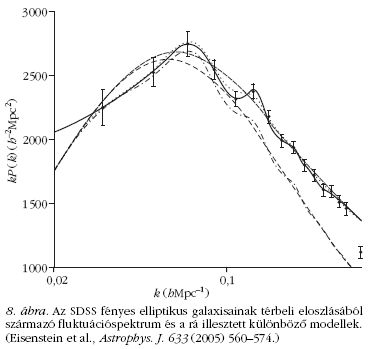
Az úgynevezett fényes elliptikus galaxisok a sötét
anyag völgyekben összegyűlő galaxishalmazok központi
objektumai, ezért viszonylag jó nyomjelzői a
sötét anyag eloszlásának. Mivel fényesek, elég nagy
távolságban is detektálni tudjuk őket, így kiválóan
alkalmasak arra, hogy eloszlásukat összevessük a
sötét anyag szimulációkból kapottakkal. A 8. ábrán
az ilyen galaxisok térbeli eloszlásának sűrűségfluktuáció
spektruma látható. Valóban felismerhetőek a
hanghullámok nyomai, sőt, a legjobban illő modell
paraméterei összhangban vannak a WMAP-észlelésekből
kapott értékekkel. Ezen kulcsfontosságú kozmológiai
eredmények mellett az SDSS "melléktermékként”
még számos érdekes új eredményt hozott, kezdve
az aszteroidák méret- és összetétel-eloszlásának
pontosabb meghatározásától a galaxisunk szerkezetének
és dinamikájának feltérképezésén át a látható
Univerzum határáról is felénk sugárzó gigantikus feketelyukakig,
melyek tanulmányozása a galaxisok
korai fejlődését teljesen átírta.
Összefoglalás
Láttuk, hogy az elmúlt évtizedben az extragalaktikus
csillagászatban és kozmológiában forradalmi átalakulások
játszódtak le. Egyre pontosabbak a kozmológiai
paraméterek mért értékei, az Univerzum és a galaxisok
fejlődésének történetét egyre részletesebben értjük,
méréseinkhez jól illeszthetőek a modellek. A forradalmi
változásokat elsősorban az észlelési lehetőségekben
bekövetkezett technológiai ugrásnak, és az adatok feldolgozását,
valamint a részletes szimulációkat lehetővé
tevő informatikai fejlődésnek köszönhetjük. Ez a technológiai
fejlődés, amennyire előre láthatunk, folytatódni
fog. Számos nagyszabású terv van folyamatban,
amelyek ha megvalósulnak, számos új műhold és gigantikus
távcső fogja ontani az új mérési adatokat az
elektromágneses tartomány minden részében, sőt, akár
a gravitáció hullámait is észlelni tudjuk.
Persze szükségünk is van minél több adatra, hiszen ne
feledkezzünk meg arról, hogy bár a modell körvonalai
pontosan illeszkednek a mérésekhez, az energiamérleg
nagy részét kitevő sötét energiáról és sötét anyagról
vajmi keveset tudunk. Ahhoz, hogy a beáramló adatokat
hatékonyan kezelni tudjuk, és ki tudjuk belőle hámozni
e rejtélyek megoldását, sok-sok olyan lelkes jövendő
kutatóra van még szükségünk, akik a hagyományos matematikai
és szaktudományos ismeretek mellett fejlett
informatikai tudással is fel vannak vértezve.
 A következő szakaszban a struktúraképződés szempontjából
újabb, fontos jelenségek játszódnak le. Az
Univerzum ekkor forró, táguló ionizált gáznak tekinthető.
A magas hőmérséklet miatt a fotonok dominálják az
eseményeket egészen az Univerzum nagyjából 380 ezer
éves koráig. A fotonoknak nagyon rövid a szabad úthosszuk,
nagyon gyakran ütköznek. A rendszer állapotegyenletét és dinamikáját
megvizsgálva kiderül, hogy
ebben a plazmában olyan rezgések
indulnak be, amelyek
leginkább akusztikus rezgésekhez
hasonlatosak, és ezért
hanghullámoknak nevezik
őket. Ezek azért fontosak,
mert, mint ahogy látni fogjuk,
a hanghullámok sűrűségfluktuációkat
okoznak, és ezek
nyoma még a jelenlegi galaxiseloszlásban
is kimutatható.
Miután a plazma annyira lehűlt
és kiritkult, hogy kialakulhattak
az első atomok, és a fotonok
szabadon repülhettek,
egyre inkább a gravitáció vette
át a struktúra formálásában a
vezénylést. A kezdeti kis sűrűségfluktuációk
a gravitáció
vonzása alatt egyre növekedtek.
A jelenlegi, úgynevezett
hideg sötét anyag modell
(Cold Dark Matter, CDM) szerint
a sötét anyag gravitációs
völgyeket hozott létre, és az
ebbe belezuhanó hidrogéngáz
addig sűrűsödött, míg begyulladtak
az első csillagok, és/vagy az első aktív galaxismagok.
Erről a "sötét” korszakról
jelenlegi műszereinkkel nem
tudunk sokat megállapítani a
semleges hidrogéngáz elnyelése miatt. A csillagok ultraibolya
fénye később ionizálta a semleges hidrogént,
valamint a szupernóva-robbanások legyártották a nehezebb
elemeket is. A kisebb galaxiskezdemények összekapcsolódtak,
és a fokozatos összeolvadások során kialakultak
a ma is látható galaxisok.
A következő szakaszban a struktúraképződés szempontjából
újabb, fontos jelenségek játszódnak le. Az
Univerzum ekkor forró, táguló ionizált gáznak tekinthető.
A magas hőmérséklet miatt a fotonok dominálják az
eseményeket egészen az Univerzum nagyjából 380 ezer
éves koráig. A fotonoknak nagyon rövid a szabad úthosszuk,
nagyon gyakran ütköznek. A rendszer állapotegyenletét és dinamikáját
megvizsgálva kiderül, hogy
ebben a plazmában olyan rezgések
indulnak be, amelyek
leginkább akusztikus rezgésekhez
hasonlatosak, és ezért
hanghullámoknak nevezik
őket. Ezek azért fontosak,
mert, mint ahogy látni fogjuk,
a hanghullámok sűrűségfluktuációkat
okoznak, és ezek
nyoma még a jelenlegi galaxiseloszlásban
is kimutatható.
Miután a plazma annyira lehűlt
és kiritkult, hogy kialakulhattak
az első atomok, és a fotonok
szabadon repülhettek,
egyre inkább a gravitáció vette
át a struktúra formálásában a
vezénylést. A kezdeti kis sűrűségfluktuációk
a gravitáció
vonzása alatt egyre növekedtek.
A jelenlegi, úgynevezett
hideg sötét anyag modell
(Cold Dark Matter, CDM) szerint
a sötét anyag gravitációs
völgyeket hozott létre, és az
ebbe belezuhanó hidrogéngáz
addig sűrűsödött, míg begyulladtak
az első csillagok, és/vagy az első aktív galaxismagok.
Erről a "sötét” korszakról
jelenlegi műszereinkkel nem
tudunk sokat megállapítani a
semleges hidrogéngáz elnyelése miatt. A csillagok ultraibolya
fénye később ionizálta a semleges hidrogént,
valamint a szupernóva-robbanások legyártották a nehezebb
elemeket is. A kisebb galaxiskezdemények összekapcsolódtak,
és a fokozatos összeolvadások során kialakultak
a ma is látható galaxisok.
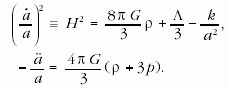
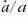 arány, a Hubble-paraméter megmondja, hogy
adott távolságon lévő két pont milyen látszólagos
sebességgel távolodik egymástól. Ezt a távolodást
mérésekkel is ki lehet mutatni, és a Hubble-törvény
értelmében egy tőlünk D távolságra lévő galaxis látszó
radiális távolodási sebessége v = H · D. Itt jegyezzük
meg, hogy sem a távolságot, sem pedig a távolodási
sebességet nem lehet közvetlenül mérni, ezek
észlelése volt az elmúlt évtizedek egyik nagy kihívása
a kísérleti kozmológiában. A jobb oldalon az első tag
az anyag hatását írja le, G a gravitációs állandó, ρ
pedig az anyagsűrűség, magában foglalva a barionikus
anyagot, a fotonokat és a sötét anyagot is. Gyakran
a sűrűséget nem közvetlenül, hanem a
arány, a Hubble-paraméter megmondja, hogy
adott távolságon lévő két pont milyen látszólagos
sebességgel távolodik egymástól. Ezt a távolodást
mérésekkel is ki lehet mutatni, és a Hubble-törvény
értelmében egy tőlünk D távolságra lévő galaxis látszó
radiális távolodási sebessége v = H · D. Itt jegyezzük
meg, hogy sem a távolságot, sem pedig a távolodási
sebességet nem lehet közvetlenül mérni, ezek
észlelése volt az elmúlt évtizedek egyik nagy kihívása
a kísérleti kozmológiában. A jobb oldalon az első tag
az anyag hatását írja le, G a gravitációs állandó, ρ
pedig az anyagsűrűség, magában foglalva a barionikus
anyagot, a fotonokat és a sötét anyagot is. Gyakran
a sűrűséget nem közvetlenül, hanem a
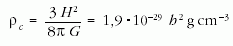
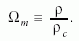
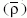 való
eltérését, azaz fluktuációit vizsgáljuk:
való
eltérését, azaz fluktuációit vizsgáljuk: