Fizikai Szemle 2007/12. 403.o.
A DEFORMÁCIÓS ANIZOTRÓPIA DISZLOKÁCIÓS MODELLJE
Ungár Tamás
ELTE Fizikai Intézet, Anyagfizikai Tanszék
A minket körülvevő világot ezernyi különböző anyag
alkotja. Ezeket a legkülönfélébb módokon próbáljuk
azonosítani, jellemezni, rendszerezni. Azt mondjuk,
hogy vannak szerves vagy szervetlen, lágy vagy szilárd,
élő vagy élettelen, vagy éppen kristályos vagy
üvegszerű anyagok. Az anyagok besorolásának talán
legnagyobb mesterei a krisztallográfusok. Ők valamikor
18. században jelentek meg, amikor a felvilágosodás
korában a természettudományok is lendületet
kaptak. Először csak azt vették észre, hogy a különböző,
a természetben található anyagokat, amelyeket
ásványoknak nevezünk, legtöbbször jól meghatározott
és mindig jellemző módon ismétlődő sík lapok
határolják. Ebből már akkor arra következtettek,
hogy ezeknek az anyagoknak feltehetően nagyon
szabályos, a természet által meghatározott szerkezete
kell, hogy legyen. Az ilyen szerkezetet kristályszerkezetnek
nevezték. Figyelemre méltó, hogy pusztán az
ásványi anyagok külső határoló lapjainak megfigyelése
alapján, elméleti geometriai és matematikai
módszerek segítségével, már az első időkben megteremtették
a krisztallográfia alapjait. Ez a tudományág
a mai napig is azzal foglalkozik, hogy leírja és meghatározza
az anyagok építőköveiben rejlő ismétlődő
szabályosságokat, a rácsperiodicitást. Itt rácson az
anyag építőköveinek rácsát kell értenünk. A 18. századtól
mintegy 200 évnek kellett eltelnie, amíg a 20.
század első éveiben, több felfedezés szerencsés összjátékának
köszönhetően, egyértelműen bizonyítottá
vált, hogy
- ) a minket körülvevő anyagok építőkövei atomok
és molekulák,
- ) ezeknek az anyagoknak igen jelentős hányada
kristályos szerkezetű,
- ) valamint, hogy ezek az anyagok olyan háromdimenziós
rácsot alkothatnak, amelyen bizonyos sugárzások
ugyanúgy elhajlanak, mint a látható fény az
optikai rácson.
Itt a „bizonyos sugárzások” azt jelenti, hogy a
sugárzás hullámhosszának az atomi méretek nagyságrendjébe,
vagyis a 0,1 nm-es tartományba vagy attól
nem túlságosan távoli tartományba kell esnie. Ettől
eltekintve a sugárzás lehet akár elektromágneses vagy
részecskesugár, nevezetesen például röntgen-, elektron-
vagy neutronsugár. Ezt a felfedezést követően,
amiért Max von Laue és két munkatársa 1911-ben Nobel-
díjat kaptak, megindult az anyagok atomi szerkezetének
szisztematikus és átfogó felderítése. Ezt a tudományágat
ma is krisztallográfiának nevezzük. A tudományág,
természeténél fogva magán hordozza a
rendszerezés jellegét, ezért már kezdetben, az 1930-as
években kialakult az egyes kutatók közötti nagyfokú
szervezettségre való törekvés. Fontossá vált, hogy
minden új kristályszerkezet felfedezése vagy meghatározása
lehetőleg minél gyorsabban közismertté váljon,
egyrészt az ismétlések elkerülése, másrészt a kristályszerkezetek
rendszereinek felépítése érdekében.
Megalakult a krisztallográfusok nemzetközi szervezete,
az International Union of Crystallographers (IUCr),
valamint létrejött a világ talán első adatbankja, az International
Centre for Diffraction Data (ICDD), a diffrakciós
adatok nemzetközi központja. A philadelphiai
(Pennsylvania, USA) központú ICDD ma már több
mint 200 000 szervetlen és szerves anyag kristályszerkezetének
adatait tartja nyilván, és ezzel a vegyipar, a
gyógyszergyártás, az élelmiszeripar, az építőipar, az
elektronikaianyag-gyártás és általában az anyagokkal
kapcsolatos bármely iparág egyik legnagyobb szolgáltató
adatbázisa. Az adatbázisban egy-egy anyag diffrakciós
spektrumának összes fontos paraméterét megtaláljuk.
A diffrakciós spektrum az anyagmintára ejtett
sugárzás (röntgen-, elektron- vagy neutronsugárzás)
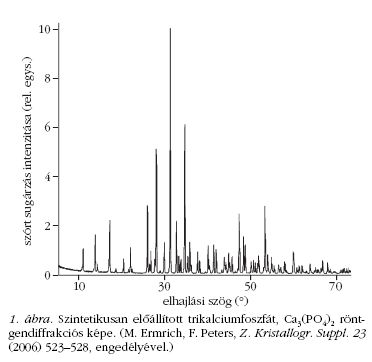
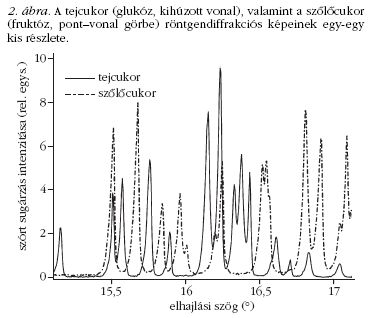
elhajlási képe. Az 1. és 2. ábra néhány tipikus elhajlási
képet (diffrakciós spektrumot, illetve képet) mutat. Ez
a két ábra jól szemlélteti, hogy az anyagok röntgendiffrakciós
képe milyen kiválóan alkalmas a különböző
anyagok azonosítására, hiszen még az amúgy rokon
anyagoknak tekinthető két cukor, a tejcukor és a szőlőcukor
röntgendiffrakciós képei is gyökeresen különböznek
egymástól, nem is beszélve a trikalciumfoszfátról.
Azt mondhatjuk, hogy a röntgendiffrakciós kép
az anyagok ujjlenyomata. Itt jegyezzük meg, hogy a
trikalciumfoszfátot a hétköznapi életben úgy ismerjük,
mint: E 341, amelyet az élelmiszeripar töltőanyagként,
lisztkezelőként, savasság szabályozóként és emulgátorként
használ.
Vegyük most pontosabban szemügyre a röntgendiffrakciós
képet. Vizsgáljuk meg a következő konkrét
példát. Az ókori egyiptomi sírok számtalan korabeli
személyes használati tárgyat tartalmaznak, amelyeket
annak idején a halottakkal együtt temettek el. A női
sírokból például százával kerültek elő különböző kozmetikumok,
többek között mindenféle fiolákban, dobozocskákban,
kerámiából vagy nádból készült tartályokban
elhelyezett arcfestékek. A párizsi Louvre régészei
elhatározták, hogy megpróbálnak utánajárni az
ókori egyiptomiak által használt arc- és szemfestékek
kémiai összetételének, sőt, ha ez lehetséges, akkor
annak is, hogy a különböző árnyalatú szemfestékeket
milyen technológiai eljárásokkal állították elő. Rögtön
kiderült, hogy az arcfestékek majd mindegyike két
alapvető összetevőt tartalmaz. Az egyik az ólomszulfid,
PbS2, köznapi nevén galenit, míg a másik az ólomkarbonát,
Pb(CO3), másnéven cerruzit. Mindkettő viszonylag
stabil, ásványi eredetű vegyület, így a bennük
lévő ólom nem jelent közvetlenül mérgező hatást.
Míg a galenit fénylő, koromfekete kristályokból áll,
addig a cerruzit fehér. A két ásvány megfelelő porításával
és keverésével előállítható a teljes fekete-fehér
színskála bármely árnyalata. Valószínűleg ez tette ezt a
két vegyületet az egyiptomi kozmetikusok számára oly
vonzóvá. Itt jegyezzük meg, hogy a galenit számos
ázsiai országban, például Indiában ma is kurrens kozmetikai
alapanyag. A kozmetikumokban a festékek,
jelen esetben a galenit vagy a cerruzit, finom por alakjában
vannak jelen úgy, hogy valamilyen olajos hordozóban
szuszpenziót alkotnak. A kémiai összetétel
meghatározása után a Louvre régészei azt a kérdést
tették fel, hogy vajon az ókori egyiptomiak milyen
módszerekkel állították elő a festékekben használt
porokat. Sok forrásmunka utalt arra, hogy a nyers ásványi
kristályokat különböző ideig tartó és különböző
intenzitású őrléssel porították, majd a szuszpenziókat
esetenként hevítették is.
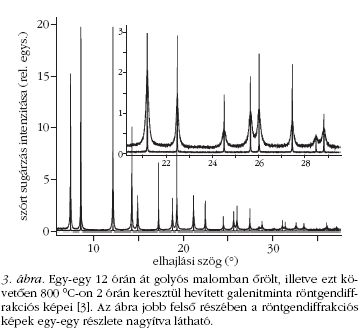
Lássuk, hogy mi történik a galenit röntgendiffrakciós
képével, ha őröljük, illetve hevítjük. Ezt mutatja a
3. ábra, amelyen egy 12 órán át nem túlságosan intenzív
őrléssel, illetve az őrlést követően 800 °C-on 2
órán keresztüli hevítéssel előállított galenitminta röntgendiffrakciós
képei láthatók [3]. A hevített, illetve a
csak őrölt minták elhajlási maximumai rendre igen
keskenyek, illetve jelentősen kiszélesedettek. Figyelemre
méltó, hogy az elhajlási maximumok pozíciói a
mérési pontosság határain belül nem változtak meg.
Az ábra jobb felső sarkában az egész elhajlási képnek
egy részlete azt mutatja, hogy milyen jelentős különbség
van a két elhajlási kép között. Az őrlésnek két
alapvető hatása van a galenit kristályokra:
- ) egyrészt a kezdetben nagyméretű, nagyjából
tökéletes kristályok elaprózódnak,
- ) másrészt az őrlés okozta mechanikai behatások
és az így végbemenő képlékeny alakváltozások nagyszámú
kristályhibát, elsősorban diszlokációkat hoznak
létre a kristályokban.
Elsősorban ez a két hatás okozza az elhajlási maximumok
kiszélesedését. A jelenség, amit a szakzsargon
vonalszélesedésnek nevez, már nagyon régen
ismert, ennek ellenére a mai napig van kutatni való
annak felderítésére, hogy milyen kapcsolat van az
elhajlási maximumok pontos alakja és az anyag mikroszerkezete
között.
Nem könnyű röviden definiálni azt, hogy mi a
mikroszerkezet. Legyen itt annyi elég, hogy olyan fizikai
tulajdonságok összessége, amelyek lényegesen
befolyásolják a konkrét anyagminta vagy anyagdarab
felhasználhatóságát. Az itt taglalt galenit esetében
mind a milliméter méretű tökéletes kristályok, mind a
finomra őrölt mikron méretű porszemcsék anyaga
galenit, de mégis, az egyik csak egy ásványdarab, a
másik viszont egy kozmetikai alapanyag. A két anyagdarab
kémiailag azonos, sőt, a kristályszerkezetük is
megegyezik, mégis a mikroszerkezetük alapvetően
különbözik.
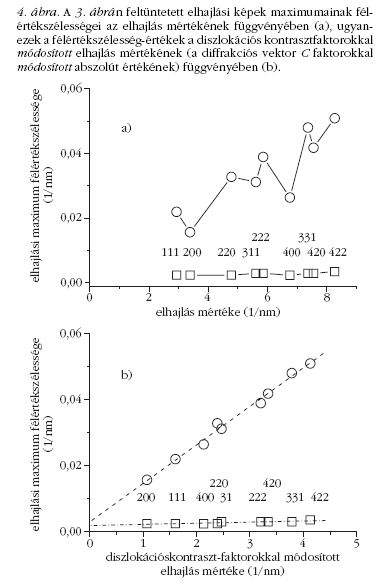
Most térjünk vissza a 3. ábrán látható elhajlási képekhez.
A két elhajlási kép közötti minőségi különbséget
számszerűen is ki lehet fejezni. Az egyik szokásos
eljárás az, hogy meghatározzuk az elhajlási maximumok
szélességét a félmaximum magasságában. Ezt
nevezzük félértékszélességnek. A 4.a ábra a két elhajlási
kép maximumainak félértékszélességeit mutatja
az elhajlás függvényében. Itt röviden meg kell állnunk,
mert, bár a mérőberendezés az elhajlást az elhajlási
szög függvényében adja meg, mind az elhajlást,
mind a maximumok félértékszélességeit a jelenség
lényege szempontjából sokkal megfelelőbb
mennyiség függvényében írjuk le. Röviden gondoljuk
végig, hogy mi is lehet ez a mennyiség. El tudjuk képzelni,
hogy egy kristályban minél kisebb az atomok
közötti távolság, az elhajlási maximumokhoz annál
nagyobb szögű elhajlás tartozik, és megfordítva,
minél nagyobb az atomok közötti távolság, az elhajlási
maximumok annál közelebb lesznek az egyenes
irányhoz. Ráadásul, az elhajlás mértéke fordítottan
arányos a röntgensugárzás hullámhosszával. Az elhajlás
lényeges tulajdonságait tehát akkor kapjuk meg
helyesen, ha az elhajlás szöge helyett a hullámhosszal
normált mennyiség függvényében írjuk le az elhajlást.
Ennek a mennyiségnek nyilvánvalóan 1/hosszúság
dimenziójúnak kell lennie. A 4.a ábrán mind a félértékszélességeket,
mind az elhajlás mértékét ilyen
mennyiség függvényében ábrázoltuk, 1/nm egységekben.
Az ilyen típusú ábrázolást, első alkalmazói után,
Williamson-Hall-ábrának nevezzük.
A mikroszerkezet legegyszerűbb modellje alapján,
ha az anyagmintában a kristályok mérete nagyon kicsinnyé
válik, akkor az elhajlási maximumok kiszélesednek.
Viszont a 4.a ábrán látható Williamson-Halltípusú
ábrázolásban a kiszélesedés mértéke ilyenkor
konstans, mindegyik maximum kiszélesedése azonos
nagyságú. Vagyis, a félértékszélességeknek ebben az
ábrázolásban egy vízszintes mentén kellene elhelyezkedniük.
Abban az esetben viszont, ha a kristályrács
el is torzul, például azért, mert diszlokációk vannak
benne, a kiszélesedés mértéke növekszik az elhajlással.
Vagyis, a félértékszélességek növekednek az elhajlással.
Azt gondolhatnánk, hogy torzult kristály
esetében ez a növekedés monoton, sőt, hogy a növekedés
mértékéből meghatározhatnánk a torzultság
mértékét, vagy akár a kristályban található diszlokációk
mennyiségét, illetve sűrűségét is.
Szemügyre véve a 4.a ábrát azt látjuk, hogy a finomra
őrölt galenitnak megfelelő félértékszélességek
növekednek ugyan az elhajlás mértékével, de ez a
növekedés korántsem monoton. A krisztallográfiában
ez a nem-monoton viselkedés a hatvanas évek óta
ismert, és a jelenség deformációs anizotrópia néven
vonult be a szakirodalomba. A „deformációs” jelző
arra utal, hogy a félértékszélességek növekednek az
elhajlás mértékével, az „anizotrópia” pedig az elhajlás
rendjében való anizotrópiát jelent. Meg lehet mutatni,
hogy a kristályrácsnak a képlékeny alakváltozással
létrehozott rácstorzulását a képlékeny alakítással létrehozott
diszlokációk okozzák. Egy korábbi cikkünkben
már foglalkoztunk a diszlokációk és a röntgen
elhajlási maximumok kiszélesedésének a kapcsolatával,
mégis, a jobb követhetőség kedvéért itt mégegyszer
összefoglaljuk azokat a dolgokat, amelyek a további
megfontolások szempontjából lényegesek.
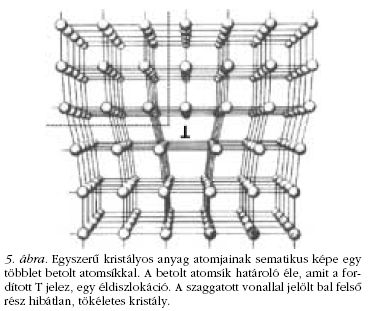
A diszlokációk egyik legegyszerűbb típusát, az
éldiszlokációt úgy képzelhetjük el, hogy az anyagot
bevágjuk az atomsíkokkal párhuzamosan egy él mentén,
majd a bevágásba, a bevágás végéig egy további
atomsíkot tolunk be. Ezt szemlélteti az 5. ábra, amelyen
a bevágás a fordított T-ig terjed. Az ábra szaggatott
vonalakkal határolt bal felső részén hibátlan kristály
látható. Az is jól látszik, hogy a diszlokáció egy
vonal mentén, a betolt többletatomsík határvonala
mentén húzódik. Ha az anyag felső és alsó részét,
nyíró erők alkalmazásával, egymáson elcsúsztatjuk,
elegendő, hogy a fordított T-vel jelölt atomsík fokozatosan
úgy mozduljon el, hogy közben mindig csak
egyetlen atomsíknyi nyírás következzen be. Ez a mechanizmus
teszi lehetővé, hogy a nyírási deformáció
300-400 GPa helyett csupán 300-400 MPa feszültséget
igényel. Az 5. ábrán jól látható, hogy a diszlokáció
környezetében különösen a függőleges atomsíkok
görbültek erőteljesen. A továbbiak szempontjából
ugyanakkor lényeges észrevennünk, hogy jelen esetben
a vízszintes atomsíkokat ez a diszlokáció szinte
érintetlenül hagyja. Azt mondhatjuk, hogy a diszlokáció
egy extrém módon anizotróp kristályhiba.
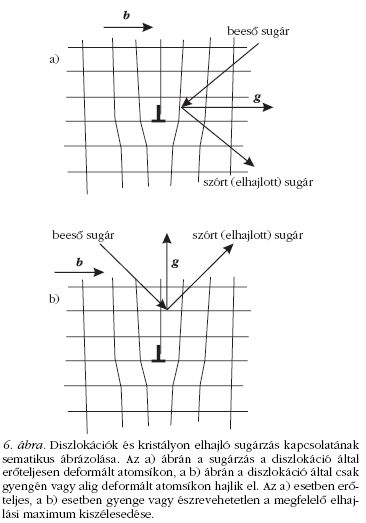
A diszlokációk és a röntgensugarak elhajlása közötti
kapcsolatok lényeges tulajdonságait a sematikus 6.
ábra jól szemlélteti. Az atomsíkokat vékony vonalakkal,
beeső és szórt (elhajlott) sugár irányát egy-egy
nyíllal, a Burgers-vektort és a diffrakciós (vagy elhajlási)
vektorokat vastag nyilakkal jelöltük. A b Burgers-vektor
a diszlokáció erősségét adja meg, a diffrakciós
vektor pedig a sugárzás elhajlását okozó atomsíkokra
(vagy hálózati síkokra) merőleges vektor. Itt jegyezzük
meg, hogy a g-vel jelölt diffrakciós vektor hossza
egyben reciproka a szóbanforgó atomsíkok távolságának.
A 6.a, illetve 6.b ábrák ugyanazt a diszlokációt
és a körülötte lévő néhány atomsíkot mutatják sematikusan.
A különbség csupán a ráeső és szórt sugárzás
irányában van. Az első esetben, ez van a 6.a ábrán, a
szórást vagy elhajlást létrehozó atomsíkok, különösen
a diszlokáció közvetlen közelében, erőteljesen torzultak,
azt látjuk, hogy el vannak görbülve. Ezzel szemben
a második esetben, ez van a 6.b ábrán, a szórást
létrehozó atomsíkok szinte teljesen érintetlenek, szép
egyenes síkok. Ennek megfelelően az első esetben az
elhajlási maximum jelentősen kiszélesedik, viszont a
második esetben szép éles marad. Ezt a jelenséget
látjuk számszerűsítve a 4.a ábrán, ahol a kiszélesedés
mértéke az egyik elhajlási maximum esetében nagyobb,
a másiknál kisebb, de globálisan mégiscsak
növekszik.
A 6. ábrán feltüntettük a Burgers- és a diffrakciós
vektorokat, b-t és g-t. Könnyen leolvasható az 6.a és
6.b ábrákról, hogy az első esetben bg ≠ 0, a másodikban
bg = 0. Ez a két vektor skaláris szorzatára vonatkozó
feltétel egyszerű eligazítást ad arra nézve, hogy
az elhajlási maximum mikor és milyen mértékben szélesedik
ki. A 6. ábra alapján kimondhatjuk azt a jól
működő szabályt, hogy amikor bg = 0, akkor az elhajlási
maximum kiszélesedése zérus vagy közel zérus,
amikor viszont bg ≠ 0, akkor az elhajlási maximum kiszélesedik,
sőt, a kiszélesedés mértéke annál nagyobb,
minél nagyobb ennek a szorzatnak a zérustól való eltérése.
Az összefüggés ennél bonyolultabb, de a jelenség
lényegének megértése szempontjából a további
részletek nem fontosak. A jelenség lényeges része az,
hogy a kiszélesedés mértéke a két vektor, b és g relatív
orientációjától függ. A 4.a és 4.b ábrákon az elhajlási
maximumokat hármas indexekkel, a Miller-indexekkel,
illetve azoknak egész számú többszöröseivel
jelöltünk. Ezek az indexek közvetlen kapcsolatban
állnak a g diffrakciós vektorral. Ezért van az, hogy az
elhajlási maximumok hol szélesebbek, hol kevésbé
szélesek, hiszen mindegyik maximum esetében más és
más az éppen aktuális g diffrakciós vektor és a vizsgált
anyagmintában lévő diszlokációk b Burgers-vektorai
közötti relatív orientáció. Elméleti és numerikus módszerekkel
pontosan ki lehet számítani, hogy mekkora
lesz a kiszélesedés mértéke, ehhez csak azt kell tudni,
hogy az anyagmintában milyen típusú diszlokációk
milyen mennyiségben vannak jelen [1, 2].
A diszlokációk okozta rácstorzulások tehát irányfüggőek,
azt mondjuk, hogy a rácsdeformáció anizotróp.
Vagyis, bizonyos kristálytani irányokban nagyobb,
más irányokban kisebb. Ugyanakkor, a szigorúan vett
irányfüggés lényegében csak a diszlokációk típusától
függ, és független az adott diszlokációk mennyiségétől
vagy sűrűségétől. Ez más szóval azt jelenti, hogy ha
megnöveljük egy bizonyos diszlokációtípus mennyiségét
a kristályban, de a diszlokáció típusát változatlanul
hagyjuk, akkor az elhajlási maximumok kiszélesedése
ugyan megnövekszik, de a deformációs anizotrópia
jellege nem változik meg. Ez gyakorlatilag azt jelenti,
hogy a deformáció irányfüggését és a rácsdeformáció
nagyságát szétválaszthatjuk. Ezt az irányfüggést összefoglalóan
egy úgynevezett diszlokációs kontrasztfaktorba
foglalhatjuk bele, amit jelöljünk C-vel. A C faktor
bármilyen diszlokációtípusra és konfigurációra
numerikus módszerekkel kiszámítható. Tudni kell
hozzá az adott anyag rugalmassági tulajdonságait, és
meg kell oldani a diszlokációk rugalmas deformációs
egyenleteit. Nyilvánvaló, hogy az olyan kristálytani
irányokban, amelyekben a diszlokációk okozta rugalmas
deformációk nagyobbak, illetve kisebbek, a megfelelő
diszlokációs kontrasztfaktorok is rendre nagyobbak,
illetve kisebbek lesznek. A 4.a ábrán az elhajlási
maximumok szélességét az elhajlás mértékének reciprokhosszúság-
egységeiben mértük fel, ez a változó
éppen a g diffrakciós vektor hosszának megfelelő paraméter.
Meg lehetett mutatni, hogy ha ezt a változót
módosítjuk a C diszlokációs kontrasztfaktorokkal,
akkor egy olyan új változót kapunk, amely éppen
azokban a kristálytani irányokban nagyobb, illetve
kisebb, amelyekben az elhajlási maximumok kiszélesedése
is rendre nagyobb, illetve kisebb. Egy ilyen
ábrázolásban, amelyet módosított Williamson-Hall-ábrázolásnak
neveztünk el [1, 2], az elhajlási maximumok
kiszélesedése monoton módon viselkedik. Ezt
mutatja a 4.b ábra, amelyen ugyanazok a szélességértékek
szerepelnek, mint a 4.a ábrán, csak a vízszintes
tengelyen a diszlokációs kontrasztfaktorokkal módosított
változót tüntettük fel. Ez az ábra azt mutatja, hogy
a deformációs anizotrópiát jól írja le e jelenség diszlokációs
modellje.
A deformációs anizotrópia diszlokációs modellje,
azon túl, hogy helyesen adja meg a jelenség fizikai
okát, számos új lehetőséget tár fel magának a jelenségnek
a felhasználására. Ez a lehetőség abban rejlik,
hogy a deformációs anizotrópiát felhasználhatjuk a
diszlokációs kontrasztfaktorok kísérletes meghatározására.
Az így kapott mért kontraszt faktorokat, a
Cmérés értékeket, összehasonlíthatjuk elméletileg számolt,
Celméleti értékekkel, amelyeket különböző diszlokációtípusok,
illetve úgynevezett csúszási rendszerek
figyelembe vétele alapján tudunk numerikus módszerekkel
meghatározni. Ez a módszer tehát lehetőséget
nyújt arra, hogy képlékenyen alakított kristályos
anyagokban meghatározzuk az éppen jelenlévő diszlokációtípusokat,
illetve meghatározzuk, hogy a képlékeny
alakváltozás milyen csúszási rendszerek aktiválása
révén jött létre.
A kristályos anyagok mikroszerkezete - amelynek
egyik legfontosabb része a diszlokációszerkezet - a
képlékenységi tulajdonságokon túl nagyok sok szempontból
fontos információkat tartalmaz. A bevezetőben
láttuk, hogy a kristályos anyagok diffrakciós képe
az anyagok ujjlenyomatának tekinthető. Ebben az értelemben
a mikroszerkezet az anyagok előéletének
vagy történetének az ujjlenyomata. A diszlokációszerkezet
részletes vizsgálata alapján sok mindenre
következtethetünk.
- ) A képlékenységi tulajdonságokra, megmondhatjuk,
hogy a képlékeny alakváltozás milyen módon,
milyen diszlokációk és csúszási rendszerek aktiválása
révén megy végbe. Ez új lehetőségeket teremt bonyolult
szerkezeti anyagok, például a reaktoroknál alkalmazott
Zr-alapú ötvözetek, a repülőgép-turbinákban
használt Ti-alapú ötvözetek, vagy az autóiparban
egyre divatosabb Mg-alapú ötvözetek kutatásában és
fejlesztésében.
- ) A geológiában fontos tudni, hogy milyen diszlokációk
és csúszási rendszerek aktiválódnak a különböző
kőzetek deformációja során. Az elektronmikroszkópia
mellett az itt leírt módszer hasznos kiegészítéseket
nyújthat, különösen olyan esetekben, amikor
atmoszférikus körülmények között a vizsgált ásvány-
vagy kőzetanyag nem stabil [4].
- ) Következtethetünk arra is, hogy a vizsgált
anyagminta milyen képlékeny deformáció révén került
abba az állapotba, amelyben a vizsgálatokat
éppen végezzük. Például régészeti leletek esetében
következtethetünk arra, hogy elődeink milyen mechanikai
vagy hőkezelési eljárást alkalmaztak, fémes vagy
akár kerámia alapú tárgyaik előállításához. Az egyiptomi
szemfestékek vizsgálata például azt mutatta,
hogy az ókori kozmetikumok készítői szelíden, csak
éppen annyira őrölték meg az alapanyagaikat, hogy a
durva szemcsék eltűnjenek és csak ritkán alkalmaztak
hevítést, azt is csak legfeljebb 300 °C-nál nem magasabb
hőmérsékleteken [3].
Irodalom
- T. Ungár, A. Borbély: The effect of dislocation contrast on X-ray
line broadening: a new approach to line profile analysis. Applied
Physics Letters 69 (1996) 3173-3175.
- T. Ungár, G. Tichy: The effect of dislocation contrast on X-ray
line profiles in untextured polycrystals. Physica Status Solidi A
147 (1999) 425-434.
- T. Ungár, P. Martinetto, G. Ribárik, E. Dooryhée, Ph. Walter, M.
Anne: Revealing the powdering methods of black makeup in
Ancient Egypt by fitting microstructure based Fourier coefficients
to whole X-ray diffraction profiles of galena. Journal of
Applied Physics 91 (2002) 2455-2465.
- P. Cordier, T. Ungár, L. Zsoldos, G. Tichy: Dislocations creep in
MgSiO3 perovskite at conditions of the Earth's uppermost lower
mantle. Nature 428 (2004) 837-840.
_________________________
A Philadelphiában működő ICDD (International Committee for
Diffraction Data, Diffrakciós Adatok Nemzetközi Szervezete) 2007-
ben a szerzőnek ítélte a Hanawalt-díjat.
