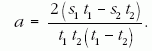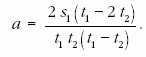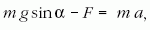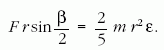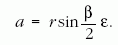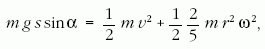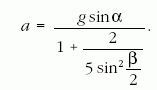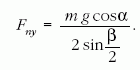Fizikai Szemle honlap

Tartalomjegyzék

Fizikai Szemle 2008/2. 65.o.

A FIZIKA OKTV HARMADIK FORDULÓJA
A HARMADIK KATEGÓRIA RÉSZÉRE - 2007
- Lejtő vályúban guruló golyó gyorsulásának vizsgálata

Vannay László, Fülöp Ferenc, Máthé József, Nagy Tamás
Budapesti Műszaki és Gazdaságtudományi Egyetem
Fizikai Intézet, Kísérleti Fizika Tanszék

A Fizika Országos Középiskolai Tanulmányi Verseny - a korábbi évekhez hasonlóan - ebben az évben is három kategóriában került megrendezésre. Külön-külön csoportban versenyeztek a szakiskolák tanulói, az általános, valamint az emelt szintű fizikaoktatásban részesülő diákok. Mind a három csoport részére három fordulóból állt a verseny. Az első két forduló során elméleti problémákat kellett megoldaniuk a versenyzőknek, míg a harmadik fordulóban mérési feladatokkal kellett megbirkózniuk. A harmadik fordulóban az első két forduló legjobbjai mérték össze tudásukat és ügyességüket.

A Budapesti Műszaki és Gazdaságtudományi Egyetem Fizikai Intézet az emelt szintű fizikaoktatásban részesülő diákok (harmadik kategória) versenyének harmadik fordulóját rendezte. A versenynek ebben a fordulójában harminc fiatal vett részt. Közleményünkben erről a versenyről számolunk be.

Dolgozatunkban bemutatjuk a versenyforduló kezdetekor kiadott írásos anyagot úgy, ahogy a versenyzők megkapták. Ennek az anyagnak a segítségével akartuk megismertetni a versenyzőket a megoldandó feladattal, és a feladat megoldásához rendelkezésükre álló eszközökkel. A kiadott írásos anyagok bemutatása után vázoljuk a kitűzött feladatok megoldásának módját, majd beszámolunk a versenyközben és az értékelés során szerzett tapasztalatokról, a versenyzők eredményeiről, és végül köszönetet mondunk mindazoknak, akik közreműködtek a verseny előkészítésében vagy lebonyolításában.

A versenyzők részére kiadott írásos anyag

Feladat
  1. Határozza meg, hogy 60°-os - függőleges szögfelezőjű - vályúszög esetén, alumíniumfelületen milyen gyorsulással mozog a sima, illetve érdesített felületű 20 mm átmérőjű acél csapágygolyó, ha a vályú lejtésszöge 5°, 10°, 15°, 20°, 25° és 30°. Mérési adatait, és a segítségükkel meghatározott gyorsulás értékeket foglalja táblázatba.
  2. Az előző pontban szereplő mérési feladatot oldja meg gumifelület alkalmazásával is.
  3. Az eddigi mérési eredményeit felhasználva, rajzolja fel a kapott gyorsulásértékeket a lejtőszög függvényében.
  4. Az előző három pontban szereplő mérési feladatot oldja meg 30°-os vályúszög esetén is.
  5. A golyók gyorsulásának meghatározásához szóba jöhető mérési eljárások közül lehetőleg olyat válasszon, amelynél az indítás bizonytalansága miatt minimális a hiba az időmérésnél.
  6. Mérési eljárásáról és az adatok feldolgozásáról készítsen jegyzőkönyvet. A jegyzőkönyv olyan részletes legyen, hogy felhasználásával minden részletre kiterjedően megismételhetők legyenek a mérései, valamint a mért adatok feldolgozása.
  7. Értelmezze és értékelje mérési eredményeit.

Megjegyzés: a vályúszög: a vályút alkotó két sík által bezárt szög, a lejtőszög: a vályút alkotó két sík egymást metsző egyenesének a vízszintessel bezárt szöge.

A feladat megoldásához rendelkezésre álló eszközök

További információk

A versenyidőtartama 4 óra.

A lejtőn leguruló golyókat lehetőleg kézzel állítsa meg a második időmérő kapu után, ne ütköztesse azokat a lejtő végét lezáró alumíniumlemezzel. Ha a kiadott eszközök kezelésével kapcsolatban problémái vannak, vagy az eszközök működésénél rendellenességet tapasztal, forduljon a felügyelő tanárokhoz.

1. ábra

A méréseket körültekintően végezze. Gondolja meg, Hogy melyik eszközt miért kapta.

Tartsa be az általános balesetvédelmi szabályokat. Vigyázzon saját maga és a kiadott eszközök épségére.

Eredményes versenyzést kívánunk.

A feladat megoldása

A versenyzők látták a rendelkezésükre álló eszközöket, közleményünk olvasóinak azonban nincs meg ez a lehetősége. Ezért mielőtt rátérnénk a feladat megoldásának ismertetésére, röviden leírjuk a kiadott eszközök listájában szereplő "berendezés"-t. A "berendezés" véglapok közé rögzíthető, két 75 cm hosszú, 25 × 25 mm-es (négyzet keresztmetszetű) alumínium-zártszelvényből áll. A zártszelvények egyik oldalára 1 mm vastag gumiréteget ragasztottunk. A zártszelvények hossztengely körüli elforgatásával egyrészt tetszőleges vályúszöget lehetett beállítani, másrészt így lehetett a vályú felületének anyagát megváltoztatni. A tengelyek egymástól való távolsága is állítható. A tengelytávolság változtatásával érhető el az, hogy a guruló golyó minden esetben a vályút alkotó síkkal érintkezzen, ne két élen gördüljön le. A két véglapot 20 mm átmérőjű alumíniumrudak fogták össze. Ezeken a rudakon lehetett az időmérő kapukat a zártszelvényekkel párhuzamosan elcsúsztatni és tetszőleges helyen rögzíteni. Ha a "berendezés" egyik véglapját az asztalon hagyjuk, és a másik véglapját a Bunsen-állványra szerelt Bunsen-fogó segítségével megemeljük, tetszőlegesen változtathatjuk a vályú hajlásszögét. Az összeállítás fényképe látható az 1. ábrán, a "berendezés" hossztengelyére merőleges metszetének vázlatát mutatja a 2. ábra.

A feladat megoldásához szükséges mérések elvégzése

  1. ) A vályúszög beállításához a mérőhelyen található két-két 30°-os, illetve 60°-os egyenlőszárú háromszög alapú fahasábot használtuk fel. A hasábokat a zártszelvények közé téve, olyan helyzetet állítottunk be, hogy a hasábok alaplapja vízszintes legyen. Ezzel biztosítottuk az elrendezés szimmetriáját a függőleges síkra. A zártszelvények tengelyének távolságát úgy állítottuk be, hogy a golyók a kialakult vályú síkjain guruljanak, de annyira kiemelkedjenek a vályúból, hogy az időmérőt működtessék.
  2. ) A lejtőszögeket a berendezés hosszának (789 mm) és a lejtőszög szinuszának ismeretében mérőszalag felhasználásával állítottuk be a Bunsen-állvány és fogó felhasználásával.
  3. ) A gyorsulások meghatározásának legegyszerűbb módja az lenne, ha megmérhetnénk azt az időt, amely alatt az álló helyzetből induló golyó egy adott utat megtesz. Az út és az idő ismeretében a gyorsulás könnyen meghatározható lenne. Ez a megoldás azonban csak közelítőleg valósítható meg, mert az időmérést indító kapu előtt a golyónak már sebessége van. A golyóindítás bizonytalanságai erősen befolyásolják a mérés eredményeit.
Mi a feladatokat az alábbiakban leírt mérések segítségével oldottuk meg.

A golyókat mindig a lejtő véglapját alkotó alumíniumlaphoz érintettük és innen indítottuk álló helyzetből. Az időmérést indító kaput, a véglaptól ismeretlen távolságban (~12 cm) rögzítettük. Feltételezhetjük, hogy adott elrendezés esetén ide mindig azonos sebességgel (v0) érkezik a golyó. A továbbiakban az indító kaputól 25 cm-es (s1), illetve 50 cm-es (s2) út megtételéhez szükséges időket (t1 és t2) mértük. A mért adatokból a keresett gyorsulás:

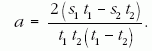
képlet

A kifejezés egyszerűsíthető, ha s2 = 2s1. Ekkor

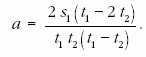
képlet

A versenyzőktől ilyen típusú megoldásokat vártunk. Egy-egy szakasz megtételéhez szükséges időt 5-ször megmérve, a feladatok megoldásához elvégzendő mérések mintegy két órát vesznek igénybe.

1. táblázat

20 mm átmérőjű csapágygolyók gyorsulása alumínium-, illetve gumifelületen, különböző vályú- és lejtőszög esetén (m/s2)
vályúszög golyófelület
és lejtőfelület 		lejtőszög
0°5°10°12,5°15°20° 25°30°
60° elmélet0,00000,3288 0,65520,81660,97651,29051,5946 1,8865
sima, alumínium
0,32500,6552
0,99081,30341,64162,0322
érdes, alumínium
0,28240,6232
 0,95241,26281,58581,8788
sima, gumi
0,17140,5303
 0,86541,20221,52521,8395
érdes, gumi
0,17350,5155
 0,83881,17361,51081,8468
30° elmélet0,00000,12260,24440,3046 0,36420,48130,59470,7036
sima, alumínium
0,09320,2172
 0,34180,46220,57560,6938
érdes, alumínium
0,06880,1894
 0,31020,43420,53940,6620
sima, gumi

0,00000,1248 0,20820,35600,50660,6338
érdes, gumi

0,06340,1334 0,20460,36220,50300,6434

Elvégeztük a méréseket úgyis, hogy út-idő-grafikont vettünk fel, a mérési pontokra másodfokú görbét illesztettünk, majd a görbe egyenletének kétszeres deriválásával határoztuk meg a gyorsulást. (Ilyen megoldást - elsősorban időigényessége miatt - nem vártunk a versenyzőktől!) Ehhez a megoldáshoz szükséges méréseket az előzőekben ismertetett eljáráshoz hasonlóan végeztük el. A golyókat mindig a véglap- tól, álló helyzetből indítottuk. Az indító kaput ugyanott rögzítettük, mint az előbb ismertetett módszernél, majd ettől a kaputól 10, 20, 25, 30, 40, 50, és 60 cm-re helyeztük a leállító kaput. Mindegyik szakasz megtételéhez szükséges időt 10-szer mértük meg és a mérési eredmények átlagát vettük figyelembe. Az időmérő elektronika a nullázásig mért idők összegét jelzi ki, így 10 mérés esetén egyszerű az átlagok meghatározása. (A kijelzőn megjelenő számot tízzel kell osztani.) A mérési pontok igen jól illeszkednek a másodfokú görbékre, a regressziós állandóra minden esetben: R2  =  1 adódott. A mérési eredmények felhasználásával kapott gyorsulásértékeket az 1. táblázat mutatja. A táblázatban szereplő gyorsulásértékeket a fent leírt mérési módokon határoztuk meg. A 60°-os vályúszögnél, gumifelületen 25 és 50 cm-es utak megtételéhez szükséges idők mérésével, a többi esetben út- idő-görbék felvételével. 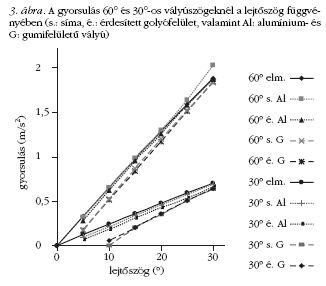A táblázat adatainak felhasználásával készült a 3. ábra.

A mérések eredményeinek értékelése előtt vizsgáljuk meg, hogy miként viselkedik a síkon mozgó golyó, ha gördül, vagy ha fúró mozgást végez.

3. ábra

Egy merev test golyó akkor gördül egy merev test síkon, ha

Ha a gördülésnél a testek nem ideális merev testek, akkor az érintkezés helyén deformáció jön létre, ami a gördülést akadályozó nyomatékot eredményez.

A merev test golyó akkor végez fúró mozgást az ugyancsak merev test síkon, ha forgástengelye, és ezzel szögsebesség vektora merőleges a síkra. Ilyenkor, mivel a golyó csak egy pontban érintkezik a síkkal, elvileg nem lép fel fékező nyomaték.

Ha a fúró mozgásnál a testek nem ideális merev testek, deformáció lép fel. Ekkor már a golyó egy felületen érintkezik a síkkal, és ez a forgást akadályozó nyomatékot eredményez.

Amikor merev test vályúban merev test golyó mozog, a golyó két pontban érintkezik a vályút alkotó síkokkal. A két pontot összekötő egyenes a golyó pillanatnyi forgástengelye, ebbe az irányba mutat a golyó szögsebesség vektora. Ennek a szögsebesség vektornak van a lejtő síkjába eső és erre merőleges komponense is. Tehát a vályúban guruló golyó gördül és egyidejűleg fúrómozgást is végez. Ideális esetet feltételezve sem a gördülés, sem a fúrómozgás miatt nem lép fel fékező nyomaték. Ilyenkor a golyóra felírt mozgásegyenletből, vagy az energiamegmaradás törvényéből meghatározhatjuk a golyó gyorsulását.

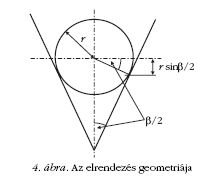
A 4. ábra jelöléseit használva, valamint a vályú és a golyó között fellépő súrlódási erőt F-fel jelölve, a golyó súlypontjára felírhatók a mozgásegyenletek. A haladó mozgásra:

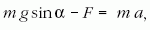
képlet

ahol α a lejtőszög, a forgó mozgásra:

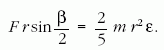
képlet

4. ábra

A gyorsulás és a szöggyorsulás (ε) közötti kapcsolat:

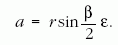
képlet

Az energiamegmaradás törvényéből:

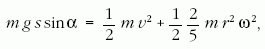
képlet

ahol v = ωr sin(β/2), s = at2/2 és v = at. Természetesen mind a két egyenletrendszerből azonos végeredményre jutunk, a leguruló golyó gyorsulása:

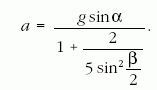
képlet

Az 1. táblázatban "elmélet" megjelöléssel szereplő gyorsulásértékeket ennek a kifejezésnek a segítségével határoztuk meg. A 3. ábrán a számított gyorsulásértékek határozzák meg az "elm" jelű görbéket. (A gyorsulás ilyen módon történő meghatározását nem vártuk a versenyzőktől.)

Ha a golyó, vagy a lejtő nem ideális merev test, a jelentkező deformációk hatására a gördülés, és az ezzel együtt jelentkező fúrómozgás következtében fékező nyomatékok lépnek fel, és ezek csökkentik a golyó gyorsulását.

A fentiek ismeretében értelmezhetők a 3. ábrán látható görbék.

A golyók viselkedése 60°-os vályúszög esetén:

Az m tömegű golyó súlyának a lejtő síkjára merőleges komponense (Fny) nagysága:

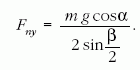
képlet

A két görbét meghosszabbítva a kis lejtőszögek irányában megint tapasztalható, hogy nem a nulla értéknél metszik a tengelyt, jelezve, hogy kis lejtőszögeknél a golyók a fékező nyomatékok miatt már nem gurulnak le. (Méréseink szerint ez az eset 2,6-°-2,8°- nál következik be.)

A golyók viselkedés 30°-os vályúszög esetén:

A mérésekkel kapcsolatos néhány megjegyzés:

A versennyel kapcsolatos tapasztalatok

Megítélésünk szerint a mérési eredmények értékelése sok tanulságot szolgáltathatott volna. Sajnálatos, hogy a versenyzőknek erre kevés idejük maradt. Reméljük azonban, hogy a verseny így is tanulságos volt, és bővítette a résztvevők fizikai ismereteit.

A harmadik fordulón elért pontszámok 40 és 16 között változtak.

A verseny végeredménye

Az összesített eredmények alapján a verseny első 11 helyezettje:

  1. VARGA GÁBOR ISTVÁN a miskolci Hermann Ottó Gimnázium diákja 91 ponttal,
  2. KÓNYA GÁBOR a Fazekas Mihály Fővárosi Gyakorló Általános Iskola és Gimnázium tanulója 90 ponttal,
  3. HUJTER BÁLINT a Fazekas Mihály Fővárosi Gyakorló Általános Iskola és Gimnázium versenyzője 89 ponttal,
  4. SZABÓ ISTVÁN a budapesti Berzsenyi Dániel Gimnázium tanulója 89 ponttal,
  5. Gilyén András (Budapest, Szent Margit Gimn., 79 pont),
  6. Tóth Dávid (Eger, Szilágyi Erzsébet Gimn. és Kollégium, 77 pont),
  7. Beck Zoltán (Fazekas Mihály Fővárosi Gyak. Ált. Isk. és Gimn., 77 pont),
  8. Roósz Gergő (Szeged, Radnóti Miklós Gyak. Gimn., 75 pont),
  9. Petrás András (Budapest, Árpád Gimn., 75 pont),
  10. Meszéna Balázs (Fazekas Mihály Fővárosi Gyak. Ált. Isk. és Gimn., 74 pont) és
  11. Farkas Ádám László (Miskolc, Földes Ferenc Gimn., 74 pont).

    Köszönetnyilvánítás

    A verseny lebonyolításához szükséges anyagi hátteret részben az Országos Közoktatási Értékelési és Vizsgaközpont biztosította. Ezt ezúton is köszönjük.

    A verseny lebonyolításához szükséges - igen munkaigényes - eszközök esztétikus kivitelezéséért Horváth Bélának és Halász Tibornak, a megfelelő körülmények megteremtéséért Gál Bélánénak és Mezey Miklósnak mondunk köszönetet. A feladat kitűzésével, a verseny lebonyolításával kapcsolatos hasznos tanácsaiért Kálmán Péternek, Keszthelyi Tamásnak és Tóth Andrásnak mondunk köszönetet.

    A versennyel kapcsolatos adminisztrációs és gazdasági ügyek intézéséért Köves Endrénét és Gál Bélánét illeti köszönet.

    Elismerés és köszönet illeti mindazokat (szülőket, tanárokat, barátokat stb.), akik segítették a versenyzők munkáját és ezzel hozzájárultak a verseny sikeréhez