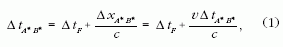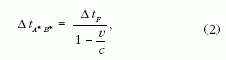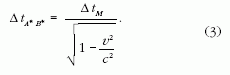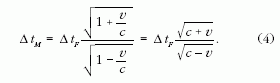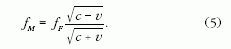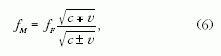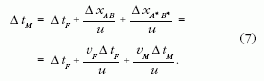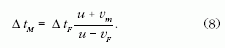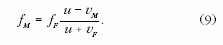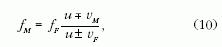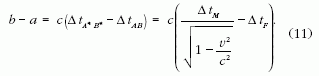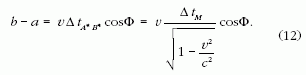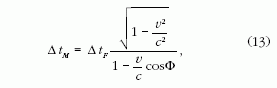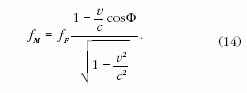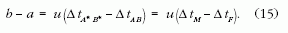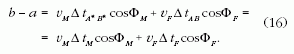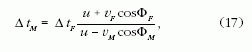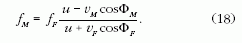Fizikai Szemle 2008/4. 142.o.
AZ ELEKTROMÁGNESES ÉS AZ AKUSZTIKAI DOPPLEREFFEKTUS
ELEMZÉSE GEOMETRIAI DIAGRAMOKKAL
Bokor Nándor
BME, Fizika Tanszék
A középiskolás diákok és az elsőéves egyetemi hallgatók,
amikor a hullámtannal ismerkednek, gyakran
találják zavarba ejtőnek az elektromágneses és az
akusztikus Doppler-formulák közötti különbséget.
Geometriai diagramoknak, valamint az "esemény"
fogalmának felhasználásával egyszerűen rá lehet világítani
a kétféle Doppler-effektus közötti matematikai
különbségek fizikai okaira.
Egydimenziós elektromágneses
Doppler-effektus
Tekintsük először az elektromágneses Doppler-effektust,
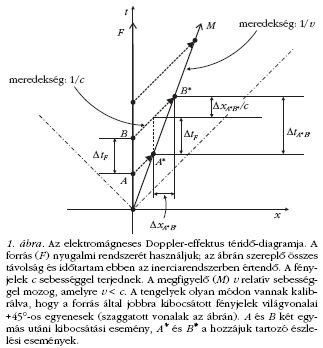
egy térbeli dimenzióban. Az 1. ábra egy
2-dimenziós (x és t ) téridő-diagramot mutat arra az
esetre, amikor a fényforrás (F) és a megfigyelő(M)
távolodik egymástól az x -tengely mentén. A forrás
és a megfigyelő mozgása is időszerű világvonallal
írható le (azaz világvonaluk mindenütt a lokális
fénykúp belsejében halad), ez megfelel annak a követelménynek,
hogy vF és vM sebességük kisebb a
fény c vákuumbeli sebességénél. Ezen a ponton kihangsúlyozandó
az a tény, hogy inerciarendszerünk
teljesen tetszőlegesen választható, mivel a fénysebesség
bármelyik inerciarendszerben c, és csak a
forrás és a megfigyelőegymáshoz képesti v sebessége
számít. Ilyen módon, az egyszerűség kedvéért és
az általánosságból semmit sem veszítve, választhatjuk
a forrás nyugalmi rendszerét, vagyis vF = 0 és
vM = v, amint az 1. ábra mutatja. Az ábra A(x,t) és
B(x,t ) pontjai két egymás utáni kibocsátási eseményt
(pl. egymás utáni fényimpulzusok vagy szomszédos
hullámfrontok elindítását) jelképezik. A hozzájuk
tartozó észlelési eseményeket az A*(x,t) és
B*(x,t ) pontok ábrázolják. A kényelem kedvéért
kalibráljuk a t- és x -tengelyeket olyan módon, hogy
bármely fényimpulzus világvonala ±45° meredekségű
egyenes vonal legyen (+45°, ha az impulzus
jobbra, és -45°, ha balra halad). Ezt elérhetjük például
úgy, ha az x -tengelyen az x = 1 métert választjuk
egységnek, a t -tengelyen pedig a t = (1 méter)/
(3 · 108 méter/másodperc) = 3,33 · 10-9
másodpercet. Az ábrán tehát a +45° meredekségű szaggatott vonalak
a forrástól a megfigyelőhöz haladó fényimpulzusok
világvonalai.
Az A és B kibocsátási események téridőbeli koordinátáit
felhasználva az A* és B* észlelési események
között eltelt idő így írható (lásd 1. ábra):
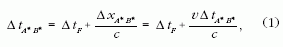
amiből
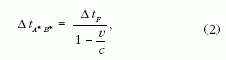
ahol ΔtF az A és B kibocsátási események között eltelt
időtartam, a nyugvó rendszerben (a forrás inerciarendszeréből)
mérve. A ΔtA* B*és a ΔtM
(az A* és B*
események között eltelt, a megfigyelő rendszerében
mért sajátidő) kapcsolatát az idődilatáció adja meg:
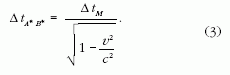
A (2) és (3) egyenletek összevetéséből:
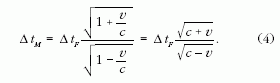
Mindkét oldal reciprokát véve megkapjuk a
megfigyelt és a kibocsátott frekvencia közötti kapcsolatot:
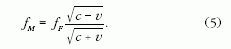
Egy hasonló téridő-diagram segítségével azt is
könnyű megmutatni (ez a diákoknak házifeladatként
feladható), hogy ha a forrás a megfigyelő felé mozog,
a (4) és (5) képletekben szereplőplusz és mínusz
előjel felcserélődik. Az egydimenziós esetre az általános
képlet tehát:
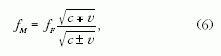
ahol a felső előjelek az egymástól távolodó forrás és
megfigyelő, míg az alsó előjelek az egymáshoz közeledő
forrás és megfigyelőesetén érvényesek.
(Egyszerű házi feladatként az is feladható, hogy a
diákok - hasonló téridő-diagramot használva - a megfigyelő
nyugalmi rendszerében tárgyalva vezessék le a
(6) képletet.)

Egydimenziós akusztikai Doppler-effektus
Ezután készítsünk a fentivel analóg téridő-diagramot
az akusztikai Doppler-jelenségre. Mivel mind a forrás,
mind a megfigyelőlassabban mozog a hang sebességénél
(különben nincs Doppler-effektus), ebben az
esetben a hang u sebessége az, ami a "természeti határsebesség".
Amikor tehát az akusztikus téridő-diagramot
készítjük, a t- és x-tengelyeket úgy kalibráljuk,
hogy a ±45° meredekségű egyenesek a hangimpulzusok
világvonalai legyenek. Ezt elérhetjük például
úgy, ha az x-tengelyen az x = 1 métert választjuk egységnek,
a t-tengelyen pedig a t = (1 méter) / (340 méter/másodperc)
= 2,94 · 10-3 másodpercet (u = 340
méter/másodperces hangsebességet feltételezve). A
Doppler-effektus feltétele, hogy mind a forrás, mind a
megfigyelő világvonala mindenütt a lokális "hangkúp"
belsejében haladjon. Ezen a ponton kihangsúlyozandó
az a tény, hogy csak egyetlen olyan inerciarendszer
van, amelyben a hangimpulzusok minden irányban
ugyanazzal az u sebességgel haladnak - és
amelyben ±45°-os világvonallal ábrázolhatók: ez az
az inerciarendszer, amelyben a terjedési közeg nyugalomban
van.
A 2. ábra egy akusztikai téridő-diagram arra az egydimenziós
esetre, amikor a hangforrás és a megfigyelő
távolodik egymástól az x-tengely mentén. A fentiekhez
hasonlóan A(x,t) és B(x,t) két egymás utáni kibocsátási
esemény (pl. két hangimpulzus vagy két egymást követő hullámfront
elindítása), A* (x,t) és B* (x,t ) pedig a
hozzájuk tartozó észlelési események. Mint az ábra
mutatja, az A* és B* között eltelt idő:
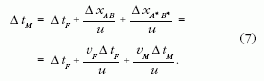
Átrendezve kapjuk:
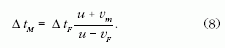
Mindkét oldal reciprokát véve kapjuk az akusztikai
Doppler-effektus ismert képletét:
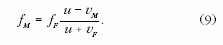
Könnyű megmutatni, hogy közeledő forrás vagy közeledő megfigyelő
esetén a (9) képletben szereplő
megfelelő előjel ellenkezőjére változik. Az egydimenziós
esetre az általános képlet tehát:
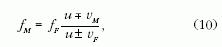
ahol felső előjelek a távolodó forrás/megfigyelő
esetében, az alsó előjelek a közeledő forrás/megfigyelő
esetében érvényesek.
Az elektromágneses és az akusztikai Doppler-képletek
levezetésének összehasonlítása
Ezen a ponton pedagógiai szempontból hasznos felkérni
a diákokat, sorolják fel az alapvető különbségeket
a kétféle levezetéshez használt téridő-diagramok
és algebrai lépések között. Ez segíti őket összpontosítani
az elektromágneses és az akusztikus hullámok,
valamint a relativisztikus és a klasszikus kinematika
közötti alapvető fizikai különbségekre. A felsorolandó
különbségek a következők:
Inerciarendszer
- Az elektromágneses hullámterjedés szempontjából
nincs preferált inerciarendszer. Minden inerciarendszer
egyenértékű, és a fény sebességét mindegyik
inerciarendszerben, bármilyen irányban ugyanolyan c
értékűnek mérjük. Ez a meglepő kísérleti tény tette lehetővé,
hogy az általánosságról való bármilyen lemondás
nélkül olyan egyszerűsített téridő-diagramot tekintsünk,
amelyben a megfigyelő nyugszik (1. ábra). Az
inerciarendszerek egyenértékűségéből következik az
is, hogy csak a forrásnak a megfigyelőhöz képesti, relatív
sebessége fog szerepelni a végső(6) képletben.
- Az akusztikus esetben azonban van preferált
inerciarendszer: az a rendszer, amelyben a hullámterjedés
közege nyugalomban van. Ez az egyetlen vonatkoztatási
rendszer, amelyben a hang sebessége izotróp,
és u-val egyenlő. Úgy döntünk, hogy téridő-diagramunkat
erre az inerciarendszerre rajzoljuk fel
(2. ábra). Az általánosság megőrzése végett a számításainkban
külön-külön figyelembe kell vennünk a
forrás mozgását és a megfigyelőmozgását (lásd 2.
ábra). Nem az egymáshoz képesti relatív sebességük,
hanem külön-külön mindkettőjük "abszolút" sebessége,
azaz ebben a preferált inerciarendszerben (a terjedési
közeghez rögzített rendszerben) mért sebességük
jelenik meg a (10) végsőképletben.
Természetes határsebesség
- Az 1. ábrán a természetes határsebesség a fény
vákuumbeli c sebessége. Mind a fényforrás, mind a
megfigyelő világvonalának a lokális fénykúpon belül
kell elhelyezkednie. A kísérleti eredmények azt mutatják,
hogy a c minden fizikai objektum számára alapvető
határsebesség. Mivel tehát v < c, a (6) képlet mindig
tényleges fizikai tartalommal bíró értéket ad fM-re.
- A 2. ábrán a "természetes határsebességet" a
hang u sebessége adja. Mind a hangforrás, mind a
megfigyelő világvonalának a lokális "hangkúpon"
belül kell elhelyezkednie. Az u hangsebesség nem
alapvető határsebesség; a természet mind a hangforrás,
mind a megfigyelő számára megengedi u túllépését.
A (10) képletben azonban a | vF | ≥ u vagy
| vM | ≥ u értékek fizikailag értelmetlen (negatív, zérus,
vagy végtelen) fM -értékekhez vezethetnek. Ezek
olyan eseteknek felelnek meg, amikor lökéshullámok
alakulnak ki és/vagy a hanghullámok nem érik el a
megfigyelőt. A Doppler-képlet ilyen esetekben nem
alkalmazható.
Idődilatáció
Az elektromágneses esetben az A* és B* események
között eltelt időtartam függ attól, melyik inerciarendszerben
mérjük. Ez az időtartam a forrás vonatkoztatási
rendszerében mérve ΔtA* B*, a
megfigyelőében mérve pedig ΔtM. A két mért érték közötti kapcsolatot
az idődilatáció (3) képlete adja meg.
Az akusztikai esetben a jelenségben szereplő összes
sebesség (lényeges módon az u "határsebességet"
is beleértve) sokkal kisebb a fénysebességnél: vF, vM, u
<< c. Az idődilatációs hatást tehát biztonsággal elhanyagolhatjuk;
ugyanazokat az időtartamokat mérjük a közeg,
a forrás és a megfigyelő vonatkoztatási rendszerében
egyaránt. A (7) egyenletben ezt használtuk ki.
Háromdimenziós elektromágneses
Doppler-effektus
Nem csak az egydimenziós, hanem az általános háromdimenziós
mozgás esetére is konstruálható téridődiagram,
amelyből az elektromágneses Doppler-képlet
általános alakja könnyen levezethető. Mivel a forrásnak
és a megfigyelőnek csak a relatív sebessége
számít, bármelyiket tekinthetjük nyugvónak. Tegyük
fel ismét, hogy a forrás van nyugalomban (helyesebben:
írjuk le a jelenséget a forrás nyugalmi vonatkoztatási
rendszerében). Tegyük fel továbbá, hogy a forrás
és a megfigyelő elegendően nagy távolságra van
egymástól, így a tárgyalt megfigyelési időtartam alatt
párhuzamos fénysugarak érik a megfigyelőt. Ekkor,
az általánosságból semmit sem veszítve, választhatjuk
az x-tengelyt úgy, hogy egybeessen a megfigyelő
mozgási irányával; és választhatjuk az y -tengelyt úgy,
hogy a hullám terjedési irányát meghatározó k hullámszámvektor
az (x,y) síkban feküdjön. Ilyen
módon az általános 3 térbeli dimenziós eset 2 térbeli
dimenzióra redukálható. A jelenség tehát teljes egészében
leírható egy 3 (2 térbeli + 1 időbeli) dimenziós
(x,y,t) téridő-diagrammal, az 1. ábra 2-dimenziós
(x,t) téridő-diagramjának analógiájára. Az érdeklődőbb
diákoknak házi feladatként feladható, hogy
konstruálják meg papíron (axonometrikus nézetben)
ezt a 3-dimenziós téridő-diagramot, és vezessék le
belőle az elektromágneses Doppler-effektus általános
képletét.
Itt azonban ismét meg kell jegyezni, hogy az
akusztikai Doppler-effektusnál a forrás és a megfigyelő sebessége
külön-külön veendő figyelembe.
Teljesen általános esetben még az sem biztos, hogy -
a hullámot szállító közeg nyugalmi rendszerében
nézve - a forrás és a megfigyelő pályaegyenese egy
síkba esik. A jelenség teljes téridőbeli leírásához tehát
egy 4-dimenziós (x,y,z,t) diagramra lenne szükség.
Téridő -diagram helyett ezért használjunk most egy
egyszerű 3-dimenziós térbeli diagramot, amelyen a
forrás és a megfigyelő (x,y,z) pályáját [nem pedig az
(x,y,z,t ) világvonalukat] fogjuk ábrázolni. A grafikus
megjelenítésből kimaradó időkoordinátát természetesen
figyelembe vesszük az algebrai levezetésben.
Mint kiderül, a térbeli diagram segítségével ismét tanulságos
összehasonlítást végezhetünk az elektromágneses
és az akusztikai eset között.
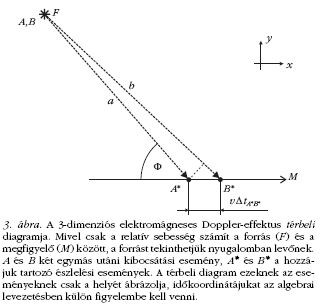
A 3. ábra az elektromágneses Doppler-effektus
térbeli diagramját mutatja, a forráshoz rögzített inerciarendszerben.
Az A-val és B-vel jelölt két egymás
utáni kibocsátási esemény ugyanazon a helyen (bár
különbözőidő pontokban) zajlik, tehát ugyanaz a
pont jelzi őket az ábrán. A hozzájuk tartozó két észlelési
esemény A* és B*. Feltesszük, hogy az A* és B*
közötti térbeli távolság elég kicsi a forrás és a megfigyelő közötti
távolsághoz képest, vagyis a tekintett
megfigyelési időtartam alatt a forrás iránya a megfigyelőhöz
képest egyetlen Φ szöggel jellemezhető.
Az ábrán szaggatott vonallal jelölt két fénysugár
úthossz különbsége:
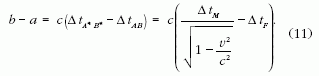
A fenti zárójel első tagjában a (3) idődilatációs
összefüggést alkalmaztuk, a második tagban pedig kihasználtuk,
hogy inerciarendszerünkben a forrás nyugalomban
van.
Ugyanez a távolság úgy is kifejezhető, mint
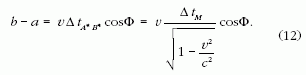
A (11) és (12) egyenletek jobb oldalát egyenlővé téve,
és a kapott egyenletet ΔtM-re megoldva kapjuk:
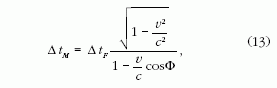
és reciprokát véve megkapjuk az elektromágneses
Doppler-effektus képletének ismert általános alakját:
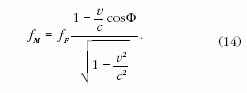
Háromdimenziós akusztikai Doppler-effektus
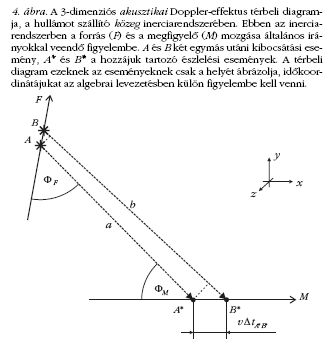
A 4. ábra (a 3. ábrán bemutatott elektromágneses eset
analógiájára) az általános, 3-dimenziós akusztikai Doppler-
effektus térbeli diagramját ábrázolja. A hullámot szállító
közeg inerciarendszerében a forrás és a megfigyelő
pályája nem szükségképpen fekszik azonos síkban. Ez
ellentétben áll az elektromágneses esettel, ahol vagy a
forrásról, vagy a megfigyelőről feltehettük, hogy nyugszik
(lásd az Inerciarendszer megjegyzést az 1-dimenziós
tárgyalásnál). Feltesszük, hogy mind az A és B kibocsátási
események közötti távolság, mind az A* és B*
észlelési események közötti távolság elegendően kicsi a
forrás és a megfigyelő közötti távolsághoz képest, azaz a
ΦF és ΦM szögek nem változnak észrevehető mértékben a
megfigyelési időtartam alatt. A két hangjel által megtett
úthosszak különbsége:
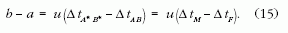
Bár Δ tA* B* és ΔtABis a hullámterjedési közeg
inerciarendszerében
mért időtartamok, mégis egyenlővé tehetők
ΔtM-mel, illetve ΔtF-fel (amelyek a megfigyelő, illetve a
forrás inerciarendszerében mért időtartamok), mert az
idődilatáció szerepét itt el lehet hanyagolni (lásd az Idődilatáció
megjegyzést az 1-dimenziós esetre).
Ugyanez a távolság kifejezhető úgy is mint
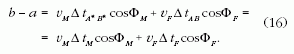
A (15) és (16) egyenletek jobb oldalát egyenlővé téve,
és a kapott egyenletet ΔtM-re megoldva kapjuk:
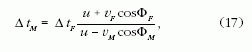
amelynek a reciprokát véve megkapjuk az akusztikai
Doppler-effektus képletének általános alakját:
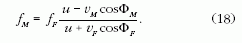
Megjegyzés
Az akusztikai Doppler-effektus általános esetének teljes
grafikai megjelenítéséhez 4-dimenziós téridő-diagramra
lenne szükség. Mivel ilyen diagramot nem tudunk a
táblára rajzolni, kénytelenek vagyunk beérni egy 3-dimenziós
térbeli diagram megrajzolásával (lásd 4. ábra),
és lemondani az időkoordináta grafikus megjelenítéséről.
Ez a szegényesebb geometriai megjelenítés is
hasznos lehet pedagógiailag az elektromágneses és az
akusztikus Doppler-képletek különbségeinek megértéséhez,
de az ábrákról bizonyos lényeges vonások óhatatlanul
hiányoznak. Amikor a diákok a két eset közötti
különbségeket sorba veszik (Az elektromágneses és az
akusztikai Doppler-képletek levezetésének összehasonlítása
pontban az 1-dimenziós esetre felírt lista analógiájára),
nincs például semmi vizuális támpont, ami a Természetes
határsebesség megjegyzésre (és a hozzá tartozó
diszkusszióra a lökéshullámokról és az információ
eljutásáról a megfigyelőhöz) utalna az ábrákból. Elképzelhető,
hogy a "kevesebb többet ér": ha csak az 1-dimenziós
eset tárgyalására szorítkozunk, a diákok általánosabb
következtetések levonására lesznek képesek.
Irodalom
E.F. Taylor, J.A. Wheeler: Téridőfizika. Typotex, Budapest, 2006.
www.mathpages.com/rr/