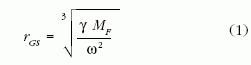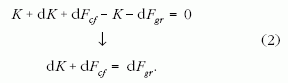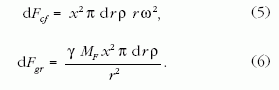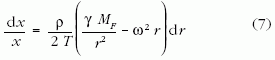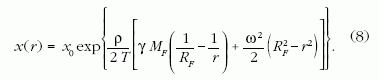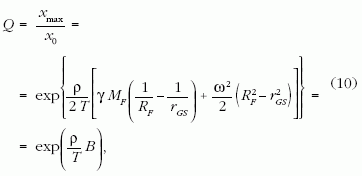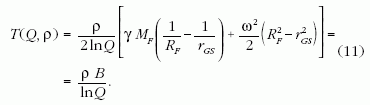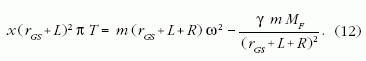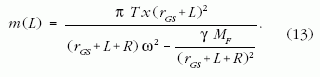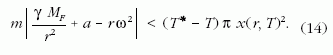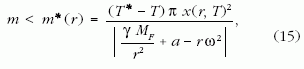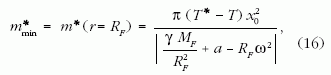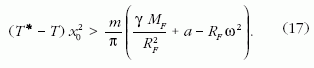Fizikai Szemle 2008/6. 229.o.
A MESEBELI ÉGIG ÉRŐ PASZULY:
AZ ŰRKÁBELEN SUHANÓ ŰRLIFT
Horváth Gábor
ELTE, Biológiai Fizika Tanszék
Az űrlift futurista víziója
A csillagászokat és űrkutatókat állandóan foglalkoztató
kérdés, hogy miként lehetne még könnyebben és olcsóbban
eljutni a világűrbe. A rakéták űrkutatásbeli
alkalmazását az elsők között Konsztantyin Eduardovics
Ciolkovszkij (1857-1935) orosz fizikus szorgalmazta.
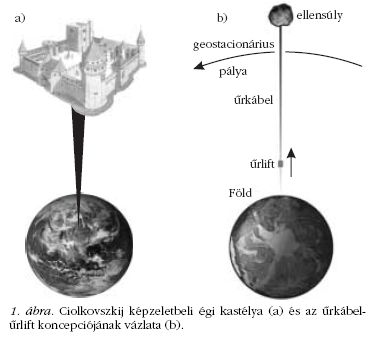
Ő vetette föl 1895-ben először egy „égi kastély”, mai
szóhasználattal egy űrállomás megépítését, amit egy
magas földi toronyhoz kapcsoltak volna egy erős kábellel
(1.a ábra). Eme „űrkábelen” egy „űrlift” szállította
volna az embereket, űreszközöket és alapanyagokat
a Föld és a magasban lebegő űrállomás között (1.b
ábra). Az űrlift első korszerű elképzelése 1960-ból Jurij
Arsutanov leningrádi mérnöktől származik, amely ötlet
azonban visszhang nélkül maradt. Az űrfölvonó ötlete a
20. századi tudományos-fantasztikus irodalomban is
föl-fölbukkant, mint például Arthur Charles Clarke
(1917-2008) angol író és mérnök Az éden szökőkútjai
(The Fountains of Paradise, 1979; magyarul, Budapest:
1993) és a 3001 - Végső űrodüsszea (3001 - The Final
Odyssey, 1997; magyarul, Budapest: 1999) című regényeiben.
Az utóbbi könyv történetében az emberek jelentős
része a Föld köré épült, összefüggő geostacionárius
gyűrűben él, amit több ponton űrkábelek kötnek
össze a Föld különböző pontjaival.
Az űrlift tervezésével régóta foglalkoznak már a csillagászok,
űrkutatók és űrmérnökök [1-4], mivel egy
ilyen űrfölvonó megépítése akár 10 000-ed részére is
csökkenthetné a világűrbe jutás költségeit. A kábelt a
Földön egy közel 50 km-es toronyhoz kötnék, valahol
az Egyenlítő mentén. Így a kábel alsó része mindig éppen
a geostacionárius pályán keringő tömegközéppont
alatt maradna, másrészt pedig az egyenlítői elhelyezés
azért is előnyös, mert a hurrikánok és erős széllökések,
amelyek egy ilyen magas torony alsóbb szintjeit veszélyeztethetnék,
elkerülik. Fölül a kábel a geostacionárius
pályán túl keringő, jókora ellensúlyhoz lenne rögzítve
(1.b ábra). Így a kábel megfeszülne a Föld forgása
miatti centrifugális erő következtében. A kifeszülő űrkábelen
„vágányok” lennének, amelyeken járművek
szállítanák az utasokat, a víz-, élelem-, illetve energiautánpótlást.
A fölfelé vezető úton megállókat lehetne
elhelyezni, ahonnan pályára állíthatók lennének a különböző
űreszközök.
Az angolul skyhooknak, azaz égi kampónak, horognak,
kapocsnak is nevezett űrlift-űrkábel két alapvető
részből áll: a fölvonófülkéből és a Föld Egyenlítője
fölött közel 36 000 km magasságban húzódó geostacionárius
körpályán túlnyúló kábelből. Az űrlift
megvalósításával elkezdődhetne az ég kolonizációja,
gyárak és telepek létesülhetnének a fejünk fölött,
több tízezer kilométer magasban.
Mindez elsőre komolytalanul hangzik, hiszen egy
több mint 36 000 km hosszú kábel előállításához még
akkor is rengeteg anyag kell, ha az csak néhány cm
vastagságú, és nem is készülhet akármiből. A kábelnek
mindenekelőtt el kell bírnia a saját súlyát. Például
egy állandó keresztmetszetű acélkötelet csak akkor
lógathatnánk le a magasból anélkül, hogy saját súlya
elszakítaná, ha a hosszúsága nem lenne nagyobb,
mint h = 20 km [4]. Ahhoz, hogy egy 1 g/cm3 sűrűségű
kötelet lelógathassunk 36 000 km magasból, az anyag
T* szakítószilárdságának 6,25 · 1010 Pa nagyságúnak
kellene lennie, ami közel százszorosa az acélénak [4].
Az űrkábel tömegét csökkenthetjük, ha a vastagságát
a magasság függvényében optimalizáljuk. A Földtől
fölfelé ugyanis egyre nőnek az anyagban föllépő húzófeszültségek,
egészen a geostacionárius pályáig,
ahol az űrkábel vastagságának maximálisnak kell lennie.
Az űrlift optimalizált alakú kábele tehát a geostacionárius
pályán „kihasasodó” (maximális), a Földhöz
rögzített végén pedig minimális átmérőjű. Ha acélból
építkeznénk, akkor a kábel maximális átmérőjének
több milliószor nagyobbnak kellene lennie, mint a
Föld felszínén. Az ilyen kábel méretei már összemérhetőek
lennének a Föld nagyobb hegyláncaival. Gyémánt
alkalmazásával a kábel maximális és minimális
vastagságának Q aránya csak 21,9 lenne, viszont a
gyémánt nagyon törékeny és drága. A zylon nevű polimerszál
esetében Q = 710, a szén nanocsőből készült
kábel viszont alig hasasodna ki, mert Q = 1,7 [4].
Az űrlift-űrkábel megtervezéséhez a nanotechnológia
vihet közelebb [4]. 1991-ben fedezték föl a fullerén
molekula előállításakor keletkező mellékterméket,
a szén nanocsöveket. E nanoméretű, lyukas hengerek
tulajdonképpen föltekeredett szénatomhálókból
állnak. A szénnek ez a módosulata rendkívüli
elektromos és mechanikai tulajdonságokkal bír. Az
űrlift szempontjából az a leglényegesebb, hogy a szén
nanocsövek szakítószilárdsága meghaladja a gyémántét
is, nagyságát T* = 1,3 · 1011 Pa-ra becsülik.
Ahhoz azonban, hogy a nanocsöveket az űrkábel
létrehozásához szükséges nagyon erős kompozitanyag
előállításához lehessen fölhasználni, legalább
néhány mm-re kellene növeszteni a hosszukat. Nagy
erőfeszítéseket tesznek a hosszabb szén nanocsövek
előállítása érdekében. A szén nanocsövekből előállítandó,
36 000 km-nél hosszabb űrkábel nagy kihívás
a tudomány számára.
A mesebeli égig érő paszuly
Szinte minden nemzet mese- és mondavilágában előfordulnak
égig érő növények, amelyeken fölmászva a
mese/mondahősök különféle csodákkal teli égi világba
juthatnak. A magyar kultúrkörben e témában megemlíthető
például Benedek Elek (1859-1929) Az égig
érő fa című meséje, Jankovics Marcell (1941-) rajzfilmrendező
Az égig érő paszuly című mesefilmje,
vagy Janikovszky Éva (1926-2003) Az égig érő fű című,
1979-ben forgatott ifjúsági filmje. Az égig érő
növény egy olyan meseelem, amely többnyire kezdő
motívum, ritkábban keretmese [5, 6]. Habár ilyen égig
érő növények a valóságban nincsenek, ha léteznének,
akkor a biomechanikájuk nagyon hasonló lenne az
űrkábel mechanikájához.
A geostacionárius keringési pálya
Amikor a Föld egyenlítőjének síkjában a gravitációs és
a centrifugális gyorsulás egyenlő, akkor egy oda helyezett
tömeg egyensúlyban van. Ez a Föld középpontjától
mért
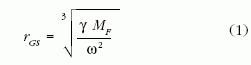
sugarú körpálya esetén teljesül, ahol γ = 6,673 ·
10-11
m3s-2kg-1 a gravitációs állandó,
ω = 7,2722 · 10-5 s-1 a
Föld forgásának szögsebessége és MF =
5,974 · 1024 kg
a Föld tömege. Az Egyenlítő fölötti, rGS sugarú kör
neve geostacionárius pálya. Az e körpályán mozgó
műhold Föld körüli keringési ideje megegyezik a Föld
tengely körüli forgásának periódusával, azaz pontosan
1 nappal. Emiatt a műhold a Földről távcsővel
nézve az Egyenlítő egy adott pontja fölött állni látszik.
Mivel a Föld átlagos sugara RF = 6,371 · 106 m,
ezért a
geostacionárius pálya az Egyenlítő fölött
H = rGS-RF = 35 872
km ≈ 36 000 km magasságban húzódik.
A minimális tömegű terheletlen űrkábel
és az égig érő paszuly alakja
Milyen alakúnak kell lennie a földi Egyenlítőhöz rögzített,
azzal együtt forgó terheletlen űrkábelnek,
amely ellensúly nélkül, csak a centrifugális erőnek
köszönhetően feszül ki? Ez nyilván csak akkor valósulhat
meg, ha a függőlegesen, azaz a Föld felületére
merőlegesen álló, alsó, földhöz rögzített végénél A
keresztmetszetű és T* szakítószilárdságú kábelre ható,
a Föld középpontjába mutató Fgr gravitációs erő és
a kábel alsó végénél ébredő, lefelé irányuló húzóerő
maximumának Fmax = AT* összege megegyezik a
Föld tengely körüli forgásából származó, sugár irányban
kifelé mutató Fcf centrifugális erővel:
Fgr+Fmax = Fcf.
Ha Fgr > Fcf, akkor a
kábel a Föld vonzása miatt
lehullik, ha viszont Fgr+Fmax
< Fcf, akkor a kábel az
alsó, rögzített végénél elszakadva a centrifugális erő
miatt kirepül az űrbe.
Hasonló probléma merül föl egy mesebeli égig érő
növénynél is: a növény csak akkor létezhetne, ha
olyan lenne a szárának alakja, hogy a Föld rá ható
gravitációs erejének és a gyökere által kifejtett, lefelé
irányuló maximális húzóerőnek az összegét kiegyensúlyozná
a növényen ébredő, fölfelé mutató centrifugális
erő. Ekkor a növény szára nem roskadna össze a
saját súlya alatt, de a centrifugális erő sem tépné ki a
földből gyökerestül.
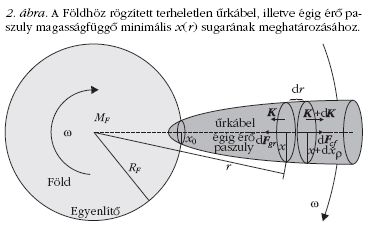
Tekintsük a Földhöz rögzített terheletlen űrkábel
(vagy égig érő paszuly) 2. ábra szerinti mechanikai
modelljét. Vegyük a homogén ρ sűrűségű, forgásszimmetrikus
kábelnek az RF sugarú és MF tömegű
Föld középpontjától r távolságra lévő elemi dr vastagságú
rétegét. E réteg r távolságra lévő alsó körlapjának
sugara legyen x(r), míg a fölső körlapjáé x+dx.
A rétegre hat a Föld középpontjába, lefelé mutató
elemi dFgr gravitációs erő, a Föld középpontjától sugárirányban
kifelé, fölfelé irányuló elemi dFcf centrifugális
erő, valamint az alsó, illetve fölső körlapján ébredő
lefelé, illetve fölfelé mutató K, illetve K+dK felületi
húzóerő, amit a kábel réteg alatti, illetve fölötti
része fejt ki. A kábel vizsgált elemi rétege akkor van
egyensúlyban, ha e négy erő eredője nulla:
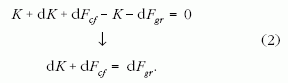
Ha a kábel 2x(r) vastagságát a tömege minimalizálása
céljából az elszakadás határáig csökkentjük, akkor a
bármely keresztmetszetén ébredő mechanikai feszültség
megegyezik a T* szakítószilárdsággal. Foglalkozzunk
azzal a speciális, matematikailag könnyebben
kezelhető esettel, amikor az űrkábel mentén végig
azonos T mechanikai feszültség ébred, vagyis amikor
T független a Föld középpontjától mért r sugártól.
Ekkor a kábel elemi dr vastagságú rétegének alsó
körlapján
K = Tx2 π
(3)
húzóerő ébred. (3)-at x szerint deriválva megkapjuk K
elemi dK megváltozását a kábel x sugarának elemi dx
megváltozásakor:
dK = 2 T π x dx
(4)
Az elemi kábeldarabra ható centrifugális és gravitációs erők:
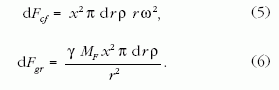
(2-6) fölhasználásával, rendezés után kapjuk a
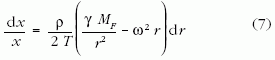
elsőrendű, szeparábilis differenciálegyenletet. Ezt
integrálva, az x (r=RF) = x0 peremfeltétel
alkalmazásával
megkapjuk a bármely keresztmetszetén T < T*
mechanikai feszültségű terheletlen űrkábel x (r) sugarát
a Föld közepétől számított r távolság függvényében:
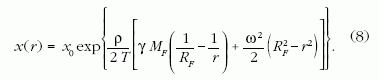
(8)-ból látható, hogy x(r=∞) = 0. Az űrkábel x(r)
sugarának azon r* távolságban van maximuma, ahol az r
szerinti első deriváltja zérus. Innen azt kapjuk, hogy

Arra az eredményre jutottunk tehát, hogy
a homogénen feszített (T = állandó) terheletlen űrkábel (égig
érő paszuly) átmérője a Föld felszínétől fölfelé haladva
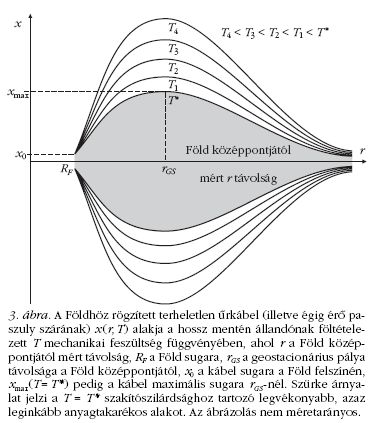
a geostacionárius pályáig (r < rGS ) egyre nő, onnantól
(r > rGS) pedig fokozatosan csökken, tehát a
kábel a geostacionárius pályán a legvastagabb. (8) és
(9) alapján megkapjuk a kábel „kihasasodásának”
mértékét, vagyis a geostacionárius távolságbeli xmax
legnagyobb sugarának és a földfelszíni x0 sugarának
Q = xmax/x0 =
x(rGS)/x0 arányát:
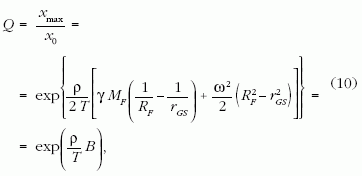
ahol B = 2,6337 · 108 m2/s2.
(10)-ből kifejezhetjük azt a T(Q ρ) állandó mechanikai feszültséget,
ami az űrkábel
mentén ébred adott Q kihasasodás és ρ sűrűség
mellett:
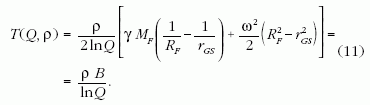
Látható (11)-ből, hogy T(Q,ρ) egyenesen arányos a ρ
sűrűséggel, és fordítva arányos a Q kihasasodás természetes
alapú logaritmusával, az arányossági tényező
pedig a Föld RF sugarától, MF tömegétől és
ω forgási
szögsebességétől függ. Vizsgáljuk meg ezek után,
hogy miként viselkedik a homogén T mechanikai
feszültségű terheletlen űrkábel (8) szerinti alakja T
változásakor. Mivel dr > 0, ezért (7) alapján a kábel
x(r) sugara elemi dx megváltozásának előjelére a következő
igaz: ha r < rGS, akkor dx > 0;
ha pedig r > rGS,
akkor dx < 0. Innen pedig az következik, hogy ha T
csökken, akkor |dx| nő. Mindennek az a végkövetkezménye,
hogy T csökkenésével Q és x(r) nő. A
3. ábra vázlatosan szemlélteti a terheletlen űrkábel (illetve
a mesebeli égig érő paszuly szárának) alakját T
függvényében. Ha az állandónak föltételezett T feszültséget
növeljük, akkor az űrkábel egyre karcsúbb,
azaz egyre anyagtakarékosabb lesz. T nem haladhatja
meg a T* szakítószilárdságot, különben elszakadna a
kábel. A 3. ábrán szürkével jelölt alak a kábel alakjának
szélsőértéke, mikor T = T*: ennél vékonyabb,
anyagtakarékosabb, kisebb tömegű kábel elszakadás
nélkül nem képzelhető el.
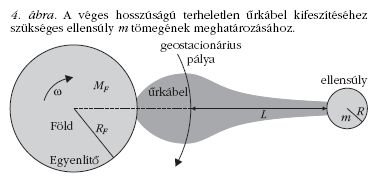
Az ellensúllyal kifeszített terheletlen űrkábel
Az űrkábel végtelen hosszát úgy rövidíthetjük, hogy a
geostacionárius pályán túl, attól L távolságban elvágjuk
és például egy gömb alakú, R sugarú, m tömegű
homogén ellensúlyhoz rögzítjük az x(rGS+L) sugarú
fölső végét (4. ábra). Az ellensúly kábelre kifejtett
gravitációs vonzóerejét elhanyagoljuk. A terheletlen
űrkábel egyensúlyban tartásához ezen fölső végénél
x(rGS+L )2πT nagyságú,
sugár irányban kifelé mutató
húzóerő szükséges, amit az ellensúlyra ható centrifugális
és gravitációs erők különbsége biztosít:
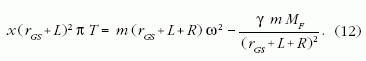
Innen az rGS+L hosszúságú terheletlen űrkábel
kifeszítéséhez szükséges ellensúly tömege:
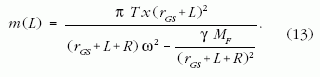
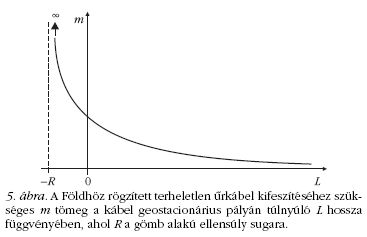
Mivel limL →+∞ x(rGS+L) = 0,
ezért (13)-ból adódik:
limL→-R m(L) = ∞, és
limL→+∞ m(L) = 0.
(13) szerinti m(L) függvényt szemlélteti vázlatosan. A
terheletlen űrkábel kifeszítéséhez szükséges m tömeg
nullához tart, amint a kábel geostacionárius pályán
túlnyúló L hossza a végtelenhez közelít, továbbá m
végtelenhez tart, amint L megközelíti -R-et.
Az űrkábel és az égig érő paszuly
terhelhetősége
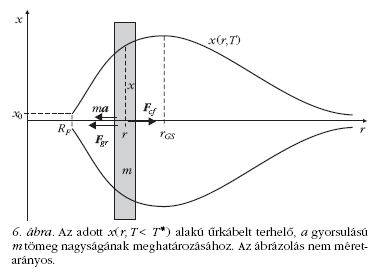
Az űrkábel fő rendeltetése a magasba történő teherszállítás,
mint ahogy a mesebeli égig érő paszulyra is
fölmászik a mesehős. Határozzuk meg ezért, hogy
adott x(r,T < T*) alakú, terheletlenül homogénen
feszülő űrkábel a Föld közepétől r távolságban mekkora
m tömeggel terhelhető, ha e tömeg a gyorsulással
mozog a 6. ábra szerinti módon. Mivel a kábel
addig terhelhető, amíg az x(r,T)2π nagyságú keresztmetszetén
ébredő T mechanikai feszültség nem haladja
meg a T* szakítószilárdságot, ezért az r helyen a
kábelre maximum Fmax = (T * -T)πx(r,T)2
többleterő
hathat. A kábel addig nem szakad el, amíg az a gyorsulással
mozgó m tömegre ható Fgr = γ
mMF /r2 gravitációs
erő, az m a tehetetlenségi erő és az Fcf =
m rω2
centrifugális erők (6. ábra) különbségének abszolút
értéke kisebb, mint Fmax:
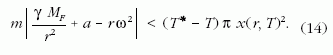
Innen kapjuk:
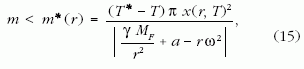
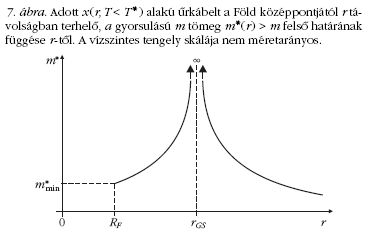
ahol x(r,T) kifejezését (8) adja. A (15) szerinti m*(r)
tömeg változását r függvényében a 7. ábra mutatja.
Látható, hogy limr→rGS m*(r) = +∞,
és mivel m*(r) az RF ≤ r ≤ rGS
tartományban monoton nő, ezért ott m*
minimuma:
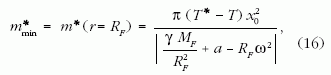
mert x(r=RF) = x0. Az űrkábel
tehát a Föld felszínén
terhelhető a legkisebb m*min tömeggel, és mivel a
centrifugális erő fölfelé nő, míg a gravitációs erő csökken,
ezért egyre följebb fokozatosan nagyobb tömeggel lehet
terhelni a 7. ábra szerinti módon. A geostacionárius pályán
a teher akármekkora lehetne, hiszen ott súlytalansági
állapot uralkodik a Földdel együtt forgó koordinátarendszerben.
Ha tehát a Földről akarunk egy terhet az
űrkábelen szállítani a geostacionárius pályán keringő
űrállomásra, s a teher a kábelen való közlekedése során
legföljebb a gyorsulással mozoghat (gyorsulhat: a > 0
vagy fékeződhet: a < 0), akkor a teher tömege nem lehet
nagyobb, mint a (16) szerinti m*min Innen adódik:
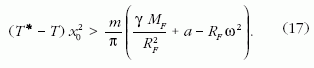
(17) ad lehetőséget a terhelhető űrkábel tervezésére:
ha ismerjük, hogy mekkora m tömegű terhet szeretnénk
az űrkábelen a geostacionárius pályára fölvontatni,
s tudjuk, hogy közben a teher legföljebb mekkora
a gyorsulással mozoghat, akkor (17)-ből T, illetve
x0 ismeretében x0, illetve T értéke kiszámítható,
aminek fölhasználásával megkapható az m tömeggel
terhelhető űrkábel (8) szerinti x(r) alakja.
Irodalom
- J. D. Isaacs, A. C. Vine, H. Bradner, G. E. Bachus: Satellite elongation
into a true „sky-hook”. Science 151 (1966) 682-683.
- V. Lvov: Sky-hook: old idea. Science 158 (1967) 946-947.
- K. E. Ebisch: Skyhook: another space construction project.
American Journal of Physics 50 (1982) 467-469.
- Babcsán N., Somogyvári B.: Anyagtudománnyal átívelt távolságok.
Természet Világa 136 (2006) 348-350.
- Berze-Nagy J.: Égigérő fa. in Magyar mitológiai tanulmányok.
Pécs, 1958.
- Diószegi V.: A honfoglaló magyarság hitvilágának történeti rétegei
- A világfa. in Népi Kultúra - Népi Társadalom. Budapest, 1969.