Fizikai Szemle 2008/6. 217.o.
SZOCIOFIZIKA: HUMÁN KAPCSOLATOK HÁLÓZATA
NAGY SKÁLÁN
Palla Gergely
MTA-ELTE Statisztikus és Biológiai Fizika Tanszék
Kertész János
BME Fizikai Intézet
A hálózatkutatás igazi multidiszciplináris tudomány,
matematikusok, fizikusok, vegyészek és biológusok
egyaránt hozzájárulnak. A „kemény” tudományok művelőit
talán meglepi, de ez a terület sokat köszönhet a
szociológiának is, amelynek keretében már a 30-as
évektől kezdve tanulmányoztak emberek kis méretű
kapcsolati hálózatokat, és fontos felismeréseket tettek.
(Itt meg kell említeni a világhírű Mérei Ferenc nevét.)
Az adatgyűjtés alapvető eszközei a kérdőívek
voltak. Az ilyen vizsgálatok előnye, hogy a kapcsolatokról
nagyon részletes információkat lehet kapni: milyen
az ismeretség, milyen erős a kapcsolat, mennyire
kölcsönös, érzelmileg hogyan viszonyulnak egymáshoz
a vizsgált személyek stb. Ezzel szemben nagy hátrány,
hogy az ilyen módon tanulmányozható minta
mérete erősen korlátozott, továbbá a válaszokból a
szubjektivitást nem lehet teljesen kiszűrni.
A hálózati megközelítés közben nagy sikereket hozott
biológiai, technológiai és gazdasági problémák vizsgálatánál
is, amelynek eredményeként mára a komplex hálózatok
témaköre önálló, interdiszciplináris tudományterületté
fejlődött [1]. Fontos szerep jutott ezen a téren a fizikusoknak
is, ugyanis a sok kölcsönható alegységből álló
rendszerek tárgyalására kidolgozott statisztikus fizikai
megközelítés rendkívül gyümölcsözőnek bizonyult. Ez a
fajta megközelítés több fontos új eredménnyel bővítette
a korábbi, kisméretű társaskapcsolat-hálózati mintákon
szerzett ismereteket. Az információtechnológia utóbbi
két évtizedben bekövetkezett rohamos fejlődésének köszönhetően
olyan új lehetőségek nyíltak meg az emberi
kapcsolathálózatok feltérképezésére, amelyek révén akár
több millió személyt tartalmazó
minták is vizsgálhatók.
A továbbiakban egy több
mint 4 millió fős mobiltelefonhívási
hálózat legfontosabb statisztikus
tulajdonságait ismertetjük.
A kérdőíves adatgyűjtéssel
szemben itt csak korlátozott
és közvetett, de ugyanakkor
objektív információ áll rendelkezésre
az egyes kapcsolatokat
illetően: kéthetes periódusokra
aggregálva a hívások
száma, összesített ideje és költsége.
Ezeket az adatok alapján
megszerkesztett hálózatban az
adott kapcsolat erősségére jellemző
élsúlyként lehet szerepeltetni.
A nem személyes ismeretséghez
kötődő hívások
kiszűrésének érdekében csak
azokat a kapcsolatokat vettük
figyelembe, amelyeknél mindkét
irányban volt hívás.
A súlyozott hálózatok fontos
jellemzői a csúcsok fokszám- és súlyerősség-eloszlása.
(Egy adott csúcs fokszáma a kapcsolatainak száma,
míg erőssége a hozzá kapcsolódó élek súlyainak
összege.) A vizsgált telefonhívási hálózat esetén
mindkét eloszlás lassan cseng le [2, 3]. Ez arra utal,
hogy ugyan csekély számban, de vannak a hálózatban
olyan csúcsok, amelyek kiugróan sok kapcsolattal,
illetve nagy erősséggel rendelkeznek.
A fokszámeloszlás és a súlyerősség-eloszlás hasonló
viselkedése felveti azt a kérdést, hogy mennyire
korrelált ez a két mennyiség. Amennyiben semmilyen
korreláció nem lenne egy adott csúcshoz kapcsolódó
élek súlya és a csúcs fokszáma között, akkor a csúcs
erősségét jól becsülhetnénk fokszámának és a teljes
hálózaton mért átlagos élsúly szorzataként. Ezzel
szemben a tapasztalat azt mutatta, hogy a csúcsok
erőssége a fokszámmal a lineárisnál lassabban nő,
ami azt jelenti, hogy aki sok ismerőssel folytat telefonbeszélgetéseket,
annak általában kevesebb ideje marad
egy-egy emberre [2, 3].
A fentiek alapján természetesen adódik az a kérdés,
hogy mi határozza meg az élek erősségét egy
társas kapcsolati hálózatban? M. Granovetter, a szociális
hálózatok egyik legnevesebb amerikai kutatója
a következő érdekes hipotézissel állt elő még a hetvenes
években [4]:
- két ember kapcsolatának erőssége az egymásnak
szentelt idő, anyagi ráfordítás, érzelmi intenzitás, bizalom
és kölcsönös segítség/szívesség kombinációja,
- és ez monoton növekvő függvénye a két ember
közös ismerősei relatív hányadának a kettejük összes
ismerőséhez viszonyítva. Ez utóbbi mennyiséget a két
személy relatív élátfedésének nevezzük.
A tanulmányozott mobilhívási hálózat ideális terepet
nyújt ezen hipotézis nagy skálájú vizsgálatára. Az
élek súlya (a hívások ideje vagy száma két felhasználó
között) ugyan nem ad lehetőséget például a felhasználók
közötti bizalom felmérésére olyan módon mint
egy kérdőíves szociometria, de tartalmazza a Granovetter-
féle erősség néhány elemét (idő-, illetve anyagi
ráfordítás), és így várhatóan jól tükrözi a kapcsolatok
intenzitását, erősségét; a mintában szereplő csúcsok
rendkívüli nagy száma pedig jó statisztikát biztosít. Az
eredmények egy, a kötések 95%-áig határozottan
emelkedő relatív átfedési görbét mutattak az élsúly
függvényében [2, 3], azaz a hipotézis beigazolódott.
Ezen eredmény révén igen szemléletes, kvalitatív
képet kaphatunk a hálózat felépítéséről. Az erős élek
olyan személyeket kötnek össze, akiknek viszonylag
sok a közös ismerőse, így várhatóan egy közösséghez
(baráti kör, család stb.) tartoznak. Ezzel szemben a
gyenge élek olyan csúcsokat kötnek össze, amelyeknek
kicsi a relatív élátfedése, ezért várhatóan más-más
közösségek tagjai. Másként megfogalmazva az erős
élek közösségek, csoportosulások összetartását jellemzik,
míg a gyenge élek a csoportokat, közösségeket
kapcsolják össze. Az erős és gyenge élek szerepének
ilyetén szétválása Granovetter másik híres hipotézise,
a gyengeél-hipotézis [4].
A fenti hipotézist igazolják a hálózat perkolációs
tulajdonságaival kapcsolatos vizsgálatok is [2, 3]. A
csúcsok 84%-a egy összefüggő, óriás komponenst alkot
a hálózatban (ezen belül bármelyik csúcsból el lehet
jutni bármely másikba az éleken keresztül), ám a hálózat
éleit fokozatosan eltávolítva, egy ponton ez a komponens
szétesik sok apró izolált csoportra (részgráfra),
amelyek mérete már elhanyagolható a teljes hálózatéhoz
viszonyítva. Ez az átalakulás megfelel a statisztikus
fizikában tanulmányozott perkoláció jelenségének. Az
óriás komponens eltűnése érdekes módon máshol következik
be attól függően, hogy az éleket milyen sorrendben
távolítjuk el. Egyik lehetőség az élsúly szerinti
emelkedő, illetve ereszkedő sorrend, vagy az él által
összekapcsolt csúcspár relatív élátfedése szerinti emelkedő,
illetve ereszkedő sorrend. Egy további lehetőséget
nyújt a sorrend kialakítására az élek köztessége is.
Egy él köztessége a hálózatban található összes lehetséges
csúcspárt összekötő legrövidebb utak közül azoknak
a száma, amelyek rajta áthaladnak.
Az átalakulás kontrollparamétere minden esetben
az eltávolított élek ρ hányada, a rendparaméter pedig
a legnagyobb összefüggő komponens (largest connected
component) RLCC relatív mérete az eredeti állapothoz
képest. Definiálható egy, a szuszceptibilitással
analóg mennyiség is,
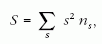
ahol ns az s méretű komponensek számát jelöli;
ennek a mennyiségnek éles csúcsa van az átalakulás
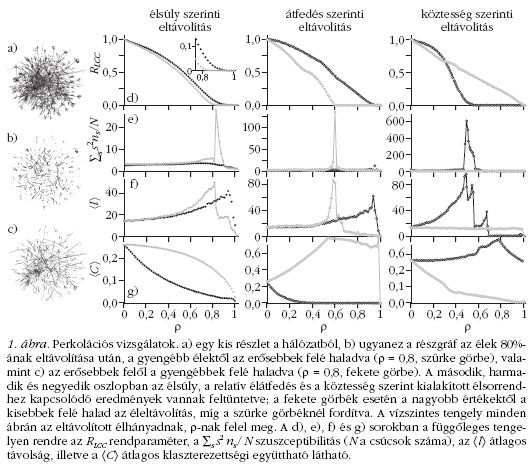
kritikus pontjánál. A vizsgálat eredményeit az 1. ábra
mutatja be. Az első oszlopban egy kisebb részgráf
látható eredeti állapotában, valamint az élek 80%-ának
eltávolítása után, egyszer a kis élsúlytól a nagyobb
felé haladva, egyszer meg ellentétes sorrendben.
A másik három oszlop a háromféle (élsúly, relatív
élátfedés, köztesség alapján kialakított) éleltávolítási-
sorrend mellett kapott eredményeket mutatja be.
A fekete színű görbéknél a hálózat ritkítása a nagy
értékkel rendelkező élektől halad a kisebb értékűek
felé, a szürke görbéknél fordítva. A rendparaméter és
a szuszceptibilitás mellet a csúcsok <l> átlagos távolsága
(minden lehetséges csúcspár közötti legrövidebb
utak átlagos hossza) és a <C> átlagos klaszterezettségi
együttható is fel van tüntetve. (Az i -ik csúcshoz
tartozó Ci az i-ik csúcs szomszédai közt lévő kapcsolatok
száma osztva a szomszédok között lehetséges
kapcsolatok maximális számával.) A görbék alapján
egy fázisátalakulás történik az él eltávolítás során,
amennyiben kis élsúlyoktól haladunk a nagyok felé,
vagy a kis relatív élátfedésektől a nagyok felé, illetve
a nagy köztességek felől a kicsik felé. (Egyrészt a
rendparaméter egy ponton lecsökken gyakorlatilag
nullára, másrészt ugyanitt egy éles csúcs jelenik meg a
szuszceptibilitásban.) Ezzel szemben nincs fázisátalakulás,
ha megfordítjuk az élkivétel sorrendjét [2, 3].
A csúcsok átlagos távolsága intenzívebben nő, ha a
kis súlyú, kis relatív élátfedésű, nagy köztességű élektől
kezdjük az élek eltávolítását (1. ábra, f) sor). Ez a
jelenség arra a hídszerepre világít rá, amit ezek az
élek betöltenek, biztosítva a sűrűbb, nagyobb élsúlyú
tartományok közti gyors összeköttetéseket [2, 3].
A klaszterezettségi együttható nagy olyan felhasználók
esetén, akiknek ismerősei egymásnak is ismerősei,
illetve kicsi ellenkező esetben. Ennek fényében
érthető, hogy <C> érzékenyen reagál arra, ha a nagy
súlyú, nagy relatív élátfedésű, kis köztességű élek
felől kezdjük a hálózat ritkítását (1. ábra, g) sor), hiszen
ezek az élek várhatóan sok háromszögben vannak
benne, és eltávolításuk drasztikusan csökkenti
<C>-t. Ezzel szemben például a kis relatív élátfedéshez
tartozó élek (a sűrű tartományokat összekötő
„hidak”) eltávolítása növeli az átlagos klaszterezettségi
együtthatót [2, 3].
Összegezve a perkolációs vizsgálatok eredményeit
azt mondhatjuk, hogy a gyengeél-hipotézis beigazolódott
nagy skálán is. Az eredeti sejtésen felül az is kiderült,
hogy az élek két eltérő szerepe, (közösségek
belső összetartása, illetve eltérő közösségek közötti
hidak létrehozása), nemcsak élsúly szerint választható
el egymástól, hanem legalább olyan jól a relatív élátfedés,
illetve a köztesség alapján is. Természetesen a
hálózati szerkezetnek mélyreható következményei
vannak az információterjedésre [2, 3].
Koncentráljunk most a már említett sűrű, erős élekkel
összetartott csoportosulásokra, közösségekre. Ezek
a való életben egy-egy baráti körnek, családnak, munkahelyi
közösségnek, vagy egyéb olyan társaságnak
felelnek meg, amelynek tagjai jól ismerik, és ennek
megfelelően gyakran hívják egymást. A hálózati csoportosulások
nagyon fontos szerkezeti egységeket
alkotnak más, például biológiai hálózatokban is, és
egyelőre nincs egy egységesen elfogadott, általános
definíciójuk. A vizsgált mobilhívási hálózat esetén a
klikk perkolációs módszerrel (clique percolation method,
CPM) történt a csoportosulások azonosítása [5].
Ez a módszer k darab csúcsból álló, teljesen összekötött
részgráfokat (k-klikkeket) használ a csoportosulások
felépítéséhez. Két k -klikket akkor mondunk
szomszédosnak, ha csak egyetlen csúcsban különböznek
egymástól, azaz k-1 csúcsuk közös. Egy CPM
segítségével kapott csoportosulás olyan k -klikkekből
épül fel, amelyek közül bármelyikből eljuthatunk
bármely másikba szomszédos k-klikkeken keresztül.
A CPM segítségével feltárt csoportosulásokon belül
az átlagos élsúly szignifikánsan magasabb értéket
vesz fel, mint a csoportok között húzódó éleken.
Emellett a felhasználókról rendelkezésre álló (igen
limitált) egyéb információk is alátámasztják a csoportosulások
hitelességét: a felhasználók kora, illetve
lakóhelyük irányítószáma egy-egy csoportosuláson
belül sokkal jobban hasonlít egymásra, mint egy
ugyanakkora, a teljes hálózatból véletlenszerűen kiválasztott
felhasználókból álló csoport esetén.
Mint említettük, a hívási adatok kéthetes időszakokra
összegezve álltak rendelkezésre, ezért lehetőség
nyílt a csoportosulások időfejlődésének tanulmányozására
[5]. Az idő előrehaladtával egy adott csoport összetétele
új tagok csatlakozásával, illetve régi tagok kiválásával
változhat, a csoport mérete nőhet vagy csökkenhet,
csoportosulások összeolvadhatnak vagy szétszakadhatnak,
teljesen új csoportok jöhetnek létre, és régiek
tűnhetnek el. Ezeket az alapvető folyamatokat szemlélteti
a 2.a ábra. Egy csoportosulás „életútját” a kéthetes
időközökkel rögzített pillanatfelvételekből kell felfűzni,
azaz a szomszédos időlépéseknél talált
csoportosulásokat egymáshoz kell illeszteni, hogy lássuk melyik
csoport mivé alakul az adott időlépés alatt.
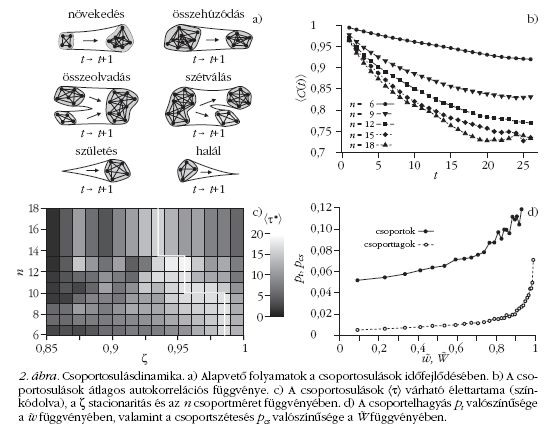
A csoportösszetétel időbeli változását a C(t ) autokorrelációs
függvény segítségével lehet egyszerűen
nyomon követni, amely a csoportosulás kezdeti és a t
időpontban tapasztalt tagösszetételeinek relatív átfedésével
egyenlő. (A relatív átfedés - a korábban tárgyalt
relatív élátfedéshez hasonlóan - a közös tagok
számának és az összes előforduló tagok számának
hányadosa.) Amennyiben a csoportosulás időben
állandó, vagy csak egy-két tagja változik, akkor C(t)
egyhez közeli értéket vesz fel, míg egy gyorsan változó
csoport esetén hamar a nullához közelít. A 2.b
ábra az autokorrelációs függvény átlagos viselkedését
mutatja különböző csoportosulás méretek esetén.
Amint látható, minél nagyobb egy csoportosulás mérete,
<C(t)> annál gyorsabban cseng le. Ez azt jelenti,
hogy a nagyobb csoportosulások relatíve gyorsabban
változnak, mint a kicsik [5].
A csoportosulások változékonyságának (vagy időtálló
voltának) jellemzésére be lehet vezetni a stacionaritás
ζ mennyiségét, amely egyszerűen a csoportosulás
szomszédos időlépésekben tapasztalt tagösszetételeinek
relatív átfedése, átlagolva a csoportosulás
életútján. Az időben nagyon stabil, keveset változó
csoportosulások egyhez közeli ζ értékkel rendelkeznek,
míg a gyakran változók alacsonyabbal, hiszen a
definícióból következően egy időlépés alatt a tagok
1-ζ hányada cserélődik ki átlagosan. A stacionaritás,
valamint az n csoportosulásméret nemtriviális összefüggésben
van a csoportosulás várható <t> élethosszával
(azon időlépések száma, amelyek alatt a
csoportosulás jelen van a hálózatban). Az élethossz
tekinthető a körülményeknek való megfelelés mértékének:
a jól megfelelő csoportosulások sokáig élnek,
a körülményekhez nem illeszkedő
csoportok hamar eltűnnek.
A 2.c ábra <τ>-t mutatja
színkódolás segítségével ζ és
n függvényében. Érdekes
módon az optimális stacionaritásérték
- ami mellett a legnagyobb
az átlagos élethossz
- alacsonyabb értékek felé
tolódik el a csoportosulás
növekvő méretével. (Ugyanezt
a viselkedést mutatták egy
másik, tudományos társszerzőségi
kapcsolatokból álló
hálózat csoportosulásai is [5].)
Ez azt jelenti, hogy a kis csoportosulások
várhatóan akkor
maradnak fenn sokáig, ha
nem változik az összetételük,
tagjaik nagyon szorosan ragaszkodnak
egymáshoz és
nem engednek be új tagokat.
Ezzel szemben a nagyméretű
csoportoknak állandóan meg
kell újulniuk a fennmaradáshoz,
ezért optimális esetben összetételük gyorsan
változik új tagok felvételével és régiek távozásával. Ez
a fajta viselkedés például nagyobb munkahelyi közösségekre,
sportklubokra jellemző, ahol rövid idő alatt
akár a teljes tagösszetétel lecserélődhet, ennek ellenére
az adott cég vagy sportklub tovább él.
Korábban bemutattuk, hogy az élsúlyok alapján
miként lehet egy-egy él hálózatban betöltött szerepére
következtetni. Az élsúlyok a csoportosulások tekintetében
is hordoznak fontos információkat, amelyek
alapján megjósolható, hogy egy adott tag milyen valószínűséggel
hagyja ott a csoportosulást, illetve, hogy
maga a csoportosulás milyen valószínűséggel szűnik
meg a következő időlépésben [5]. Ehhez célszerű definiálni
a 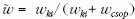 mennyiséget az egyes
csoporttagokra vonatkozóan, ahol wki az adott tag
csoporton kívüli kapcsolatainak összsúlya, míg wcsop a
csoport többi tagjához kötődő élek összsúlya. Hasonló
módon lehet a teljes csoportra vonatkozóan megadni
a
mennyiséget az egyes
csoporttagokra vonatkozóan, ahol wki az adott tag
csoporton kívüli kapcsolatainak összsúlya, míg wcsop a
csoport többi tagjához kötődő élek összsúlya. Hasonló
módon lehet a teljes csoportra vonatkozóan megadni
a 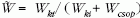 mennyiséget, ahol Wki a
csoportból a csoporton kívülre menő élek összsúlya,
valamint Wcsop a csoporton belüli élek összsúlya. A
2.d ábrán a
mennyiséget, ahol Wki a
csoportból a csoporton kívülre menő élek összsúlya,
valamint Wcsop a csoporton belüli élek összsúlya. A
2.d ábrán a 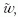 illetve a
illetve a 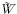 függvényében mutatjuk annak
a pt és pcs átlagos valószínűségét, hogy a következő
időlépésben az adott tag kilép a csoportból, illetve az
adott csoport felbomlik. Mindkét esetben, a természetes
várakozásnak megfelelően (miszerint minél nagyobb
a külső élek relatív súlya, annál valószínűbb a
kilépés vagy a felbomlás), a görbék emelkedő tendenciát
mutatnak.
Összefoglalva a legfontosabb eredményeket elmondhatjuk,
hogy a modern információs technológiáknak
köszönhetően megnyílt az út a nagy skálájú társas
kapcsolati hálózatok statisztikus vizsgálata előtt. A
tárgyalt több millió felhasználót tartalmazó mobilhívási
hálózat analízise igazolta a szociális hálózatok élsúlyai-
ra, illetve a gyenge élek szerepére vonatkozó hipotéziseket,
feltárta az élsúlyok, valamint a hálózat lokális és
globális szerkezete közötti összefüggést. A hálózatban
található sűrű csoportosulások időfejlődésénél érdekes
eltérés volt tapasztalható a kis és nagy méretű csoportosulások
hosszútávú túlélési stratégiájában. Ezek az
eredmények fontos kiindulópontot szolgáltatnak egyfelől
a nagy méretű társas kapcsolati hálózatok további
vizsgálataihoz, másfelől az ilyen típusú hálózatok modellezéséhez,
elméleti leírásához.
Irodalom
függvényében mutatjuk annak
a pt és pcs átlagos valószínűségét, hogy a következő
időlépésben az adott tag kilép a csoportból, illetve az
adott csoport felbomlik. Mindkét esetben, a természetes
várakozásnak megfelelően (miszerint minél nagyobb
a külső élek relatív súlya, annál valószínűbb a
kilépés vagy a felbomlás), a görbék emelkedő tendenciát
mutatnak.
Összefoglalva a legfontosabb eredményeket elmondhatjuk,
hogy a modern információs technológiáknak
köszönhetően megnyílt az út a nagy skálájú társas
kapcsolati hálózatok statisztikus vizsgálata előtt. A
tárgyalt több millió felhasználót tartalmazó mobilhívási
hálózat analízise igazolta a szociális hálózatok élsúlyai-
ra, illetve a gyenge élek szerepére vonatkozó hipotéziseket,
feltárta az élsúlyok, valamint a hálózat lokális és
globális szerkezete közötti összefüggést. A hálózatban
található sűrű csoportosulások időfejlődésénél érdekes
eltérés volt tapasztalható a kis és nagy méretű csoportosulások
hosszútávú túlélési stratégiájában. Ezek az
eredmények fontos kiindulópontot szolgáltatnak egyfelől
a nagy méretű társas kapcsolati hálózatok további
vizsgálataihoz, másfelől az ilyen típusú hálózatok modellezéséhez,
elméleti leírásához.
Irodalom
- Barabási A.-L.: Behálózva. Magyar Könyvklub, 2003.
- J.-P. Onnela, J. Saramäki, J. Hyvönen, G. Szabó, M. A. de Menezes,
K. Kaski, A.-L. Barabási, J. Kertész: Analysis of a large-scale
weighted network of one-to-one human communication. New
Journal of Physics 9 (2007) 179.
- J.-P. Onnela, J. Saramäki, J. Hyvönen, G. Szabó, D. Lazer, K.
Kaski, J. Kertész, A.-L. Barabási: Structure and tie strengths in
mobile communication networks. PNAS 104 (2007) 7332.
- M. Granovetter: The strength of weak ties. Am. J. Sociol. 78
(1973) 1360.
- G. Palla, A.-L. Barabási, T. Vicsek: Quantifying social group evolution.
Nature 446 (2007) 664.
_________________________
A szerzôk kutatásait az OTKA K68669 és K60456 jelű pályázatai
támogatták.
A szerzôk köszönettel tartoznak Szabó Gábornak, Barabási Albert-
Lászlónak és Vicsek Tamásnak, valamint az ezen cikk alapjául
szolgáló korábbi publikációk további társszerzôinek is.

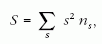
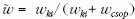 mennyiséget az egyes
csoporttagokra vonatkozóan, ahol wki az adott tag
csoporton kívüli kapcsolatainak összsúlya, míg wcsop a
csoport többi tagjához kötődő élek összsúlya. Hasonló
módon lehet a teljes csoportra vonatkozóan megadni
a
mennyiséget az egyes
csoporttagokra vonatkozóan, ahol wki az adott tag
csoporton kívüli kapcsolatainak összsúlya, míg wcsop a
csoport többi tagjához kötődő élek összsúlya. Hasonló
módon lehet a teljes csoportra vonatkozóan megadni
a 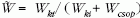 mennyiséget, ahol Wki a
csoportból a csoporton kívülre menő élek összsúlya,
valamint Wcsop a csoporton belüli élek összsúlya. A
2.d ábrán a
mennyiséget, ahol Wki a
csoportból a csoporton kívülre menő élek összsúlya,
valamint Wcsop a csoporton belüli élek összsúlya. A
2.d ábrán a 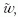 illetve a
illetve a 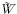 függvényében mutatjuk annak
a pt és pcs átlagos valószínűségét, hogy a következő
időlépésben az adott tag kilép a csoportból, illetve az
adott csoport felbomlik. Mindkét esetben, a természetes
várakozásnak megfelelően (miszerint minél nagyobb
a külső élek relatív súlya, annál valószínűbb a
kilépés vagy a felbomlás), a görbék emelkedő tendenciát
mutatnak.
Összefoglalva a legfontosabb eredményeket elmondhatjuk,
hogy a modern információs technológiáknak
köszönhetően megnyílt az út a nagy skálájú társas
kapcsolati hálózatok statisztikus vizsgálata előtt. A
tárgyalt több millió felhasználót tartalmazó mobilhívási
hálózat analízise igazolta a szociális hálózatok élsúlyai-
ra, illetve a gyenge élek szerepére vonatkozó hipotéziseket,
feltárta az élsúlyok, valamint a hálózat lokális és
globális szerkezete közötti összefüggést. A hálózatban
található sűrű csoportosulások időfejlődésénél érdekes
eltérés volt tapasztalható a kis és nagy méretű csoportosulások
hosszútávú túlélési stratégiájában. Ezek az
eredmények fontos kiindulópontot szolgáltatnak egyfelől
a nagy méretű társas kapcsolati hálózatok további
vizsgálataihoz, másfelől az ilyen típusú hálózatok modellezéséhez,
elméleti leírásához.
Irodalom
függvényében mutatjuk annak
a pt és pcs átlagos valószínűségét, hogy a következő
időlépésben az adott tag kilép a csoportból, illetve az
adott csoport felbomlik. Mindkét esetben, a természetes
várakozásnak megfelelően (miszerint minél nagyobb
a külső élek relatív súlya, annál valószínűbb a
kilépés vagy a felbomlás), a görbék emelkedő tendenciát
mutatnak.
Összefoglalva a legfontosabb eredményeket elmondhatjuk,
hogy a modern információs technológiáknak
köszönhetően megnyílt az út a nagy skálájú társas
kapcsolati hálózatok statisztikus vizsgálata előtt. A
tárgyalt több millió felhasználót tartalmazó mobilhívási
hálózat analízise igazolta a szociális hálózatok élsúlyai-
ra, illetve a gyenge élek szerepére vonatkozó hipotéziseket,
feltárta az élsúlyok, valamint a hálózat lokális és
globális szerkezete közötti összefüggést. A hálózatban
található sűrű csoportosulások időfejlődésénél érdekes
eltérés volt tapasztalható a kis és nagy méretű csoportosulások
hosszútávú túlélési stratégiájában. Ezek az
eredmények fontos kiindulópontot szolgáltatnak egyfelől
a nagy méretű társas kapcsolati hálózatok további
vizsgálataihoz, másfelől az ilyen típusú hálózatok modellezéséhez,
elméleti leírásához.
Irodalom