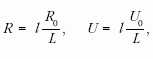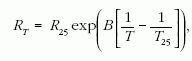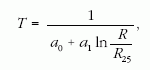Fizikai Szemle 2008/7-8. 267.o.
A VIRTUÁLIS MÉRÉSTECHNIKA KÍSÉRLETI LEHETŐSÉGEI
A KÖZOKTATÁSBAN
Kopasz Katalin, Gingl Zoltán, Makra Péter, Papp Katalin
SZTE-TTIK Kísérleti Fizikai Tanszék
"A tudomány akkor kezdődik, amikor elkezdünk mérni,
pontos tudomány mérés nélkül nem lehetséges.”
Mengyelejev
A fizika és a többi természettudományos tárgy oktatásában
is kiemelt szerepe van a kísérletezésnek, hiszen
ez szemlélteti és igazolja a modellek helyességét, segítségünkre
van az érvényességi határok megismertetésében,
és így fontos kapcsolatot teremt a tananyag
és a valódi jelenségek között. A kísérletezés a diákok
számára sokkal érthetőbbé, kézzelfoghatóbbá teszi a
gyakran bonyolult, nehezen követhető leírást, törvényeket.
Ahhoz, hogy az iskolai fizikatanítás az adott
szinten visszatükrözze a tudomány jellegzetességeit,
az életkorhoz és a tananyaghoz illeszkedő méréseket
kell beépítenünk az oktatásba.
A mérőkísérletek jelentősége megnövekedett az új
rendszerű és szellemű érettségi követelmények bevezetésével,
amelyekben ez áll:
„A vizsgázónak a követelményrendszerben és a
vizsgaleírásban meghatározott módon az alábbi kompetenciák
meglétét kell bizonyítania:
- ismeretei összekapcsolása a mindennapokban
tapasztalt jelenségekkel, a technikai eszközök működésével;
- egyszerűen lefolytatható fizikai kísérletek elvégzése,
a kísérleti tapasztalatok kiértékelése;
- grafikonok, ábrák értékelése, elemzése;
- a napjainkban felmerülő, fizikai ismereteket is
igénylő problémák lényegének megértése, a természet-
és környezetvédelemmel kapcsolatos problémák
felismerése.”
Az emelt szintű fizika érettségi vizsgán ezen túlmenően
az alábbi kompetencia is szükséges:
- „a mindennapi életet befolyásoló fizikai természetű
jelenségek értelmezése”. [1]
A fizika tanításában a kísérletek között szerepelniük
kell mérőkísérleteknek is. Az iskolai tanításban
a kísérleti eszközök gyakran elavultak és a mérésekhez
tartozó műszerek sem korszerűek. A modern
eszközök lehetőség szerinti bevonása a tanórába elengedhetetlen.
Ugyanakkor a szűkülő finanszírozás,
a korlátozott anyagi lehetőségek miatt utópisztikus
az az elképzelés, hogy taneszközgyártótól rendelt
készletek segítségével valósítsák meg a méréseket az
iskolákban.
Szimulációk, animációk bemutatásához a tanárok
egyre gyakrabban vesznek igénybe számítógépet.
Részben, mert a fizikatanításnak feladata a modern
eszközök, mérési eljárások megismertetése a tanulókkal,
ugyanakkor a számítógép motiváló hatása is jól
kiaknázható a számítógépes méréseket alkalmazó
tanítás során.
A mai informatikai lehetőségek és a hozzájuk kapcsolódó
digitális technika segítségével azonban egyszerűen
tehetjük igen hatékonnyá a kísérletező oktatást:
használjunk virtuális méréstechnikát! Ismeretével
lehetőség nyílik arra, hogy kevés anyagi ráfordítással
a tananyag bármely területéhez kapcsolódva mutassunk
be valódi kísérleteket, amelyeknél a mérés és
kiértékelés számítógép segítségével történik. Közben
a tanulók megismerik a szenzorok működését, és ízelítőt
kapnak a fizikusok munkájából is.
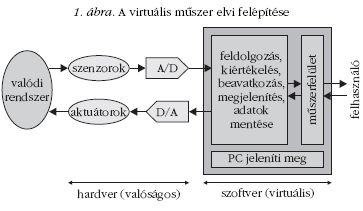
A virtuális méréstechnika lényege, hogy a valódi
jeleket (elmozdulás, hőmérséklet, nyomás stb.) szenzorok
segítségével elektromos jelekké, majd digitális
technika alkalmazásával számokká alakítjuk, így a méréshez
kapcsolódó feldolgozás, megjelenítés és más
műszerfunkciók már számítógéppel, szoftverekkel végezhetők
el [2]. Ilyen módon a valódi méréseket végző
műszer szoftveresen „realizálható”, innen ered a virtuális
méréstechnika elnevezés.
A megvalósításhoz szükséges számítógép minden
iskolában jelen van. A szenzorokat könnyen és aránylag
olcsón be lehet szerezni. A hiányzó láncszem a számítógép
és az érzékelők kapcsolatát megvalósító analóg-
digitális konverziót elvégző adatgyűjtő műszer és a
mérő szoftver (1. ábra). A közoktatás számára jelenleg
elérhető számítógépes mérőrendszerekhez képest ezt
töredékáron meg lehet valósítani, számítógéphez kapcsolásához
pedig mindössze egy USB-csatlakozó szükséges.
A virtuális műszer működése könnyen átlátható,
kevésbé hasonlít fekete dobozhoz, mint az általában
használt digitális eszközök.
Virtuális műszerek korábban is készültek LabVIEW
fejlesztői környezetben, ez azonban meglehetősen
költséges. Az alábbiakban bemutatandó műszerekhez
C# forráskódot használtunk. A gyorsan megtanulható
nyelv előnye, hogy ingyenesen hozzáférhető, és
kevés gyakorlás után is képesek lehetünk grafikus
felületeken mérőprogramokat készíteni, az elkészült
programokból akár megosztható gyűjteményt is készíthetünk.
Az iskolai gyakorlatban előforduló számítógépes
mérésekkel ellentétben a felhasználók magyar
nyelvű programokkal találkoznak, ami megkönnyíti
a tanórai felhasználásukat.

Informatika és elektronika iránt érdeklődő tanárok
kezében a fejleszthető kísérletek határait csak az idő
és a beszerezhető szenzorok szabják meg. Ugyanakkor
a fejlesztői környezet a programok fordításakor
.exe kiterjesztésű fájlokat is készít, amelyeket a jól
megszokott módon lehet használni, így a számítástechnikában
kevésbé járatos tanárok is bátran felhasználhatják
ezeket óráikon.
Az alábbiakban a Szegedi Tudományegyetem Kísérleti
Fizikai Tanszékén fejlesztett eszközökből, kísérletekből
mutatunk be néhányat, amellyel illusztráljuk
a fentebb említett módszer hatékonyságát.
Hosszúságmérés feszültségosztással
A változtatható értékű ellenállásoknál az ellenállás két
vége között egy elmozdítható érintkező (csúszka)
található, melynek helyzetétől függ a potenciométer
vége és a csúszka közötti ellenállás (2. ábra). A
csúszka helyzetének függvényében a mért feszültség
értéke is változik [3].
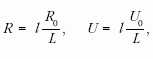
ahol L a csúszka teljes hossza, l a pillanatnyi helyzete,
U a mért feszültség, U0 az adatgyűjtő által küldött feszültség.
A mérőprogram a feszültségértékből kiszámítja a
csúszka helyzetét. Mérés folyamán az értékek számszerű
megjelenítése mellett grafikus szemléltetés is
segíti a munkát. Viszonylagos egyszerűsége miatt
alkalmas arra, hogy használatával megismerkedjünk
a rendszer működésével és a kiaknázható lehetőségekkel.
Hőmérsékletmérés termisztorral
Speciális célokra különleges, hőmérsékletfüggő ellenállások
készülnek. Az NTK (negatív temperatura koefficiensű)
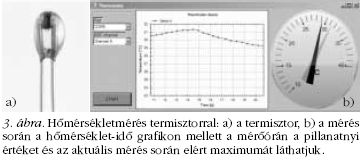
termisztorok (3.a ábra) ellenállása a hőmérséklet
növekedésével exponenciálisan csökken a következők
szerint:
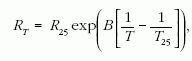
ahol R25 a 25 °C-os hőmérséklethez tartozó
ellenállás, B a termisztorra jellemző érték (táblázatból kikereshető)
T pedig abszolút hőmérsékletet jelent (T25 =
278 K). Így a hőmérséklet a következő formulából
számolható:
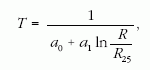
ahol a0 és a1 a termisztorra jellemző értékek. A ter-
misztorok nagy érzékenységűek, a mérendő ellenállás
kΩ nagyságrendű, így könnyű velük mérni a -40 °C
és +115 °C közötti tartományban, a kereskedelemben
készen és olcsón kaphatók [3].
A virtuális műszer kijelzőjén (a monitoron) a hőmérséklet-
idő grafikon látható; mellette megjelenik
egy mérőóra, amely a pillanatnyi hőmérsékletérték
mellett jelzi az aktuális mérés során elért maximumot
(3.b ábra).
Hőterjedés vizsgálata
Egy fémrudat nagy tömegű fémtömbbe (hőtartály)
illesztünk. A rúd mentén egyenközűen termisztoros
hőmérsékletszenzorokat helyezünk el (4.a ábra). A
fémrúd szabad végét melegítsük rövid ideig nyílt
lánggal, és mérjük a hőmérsékletet az idő függvényében!
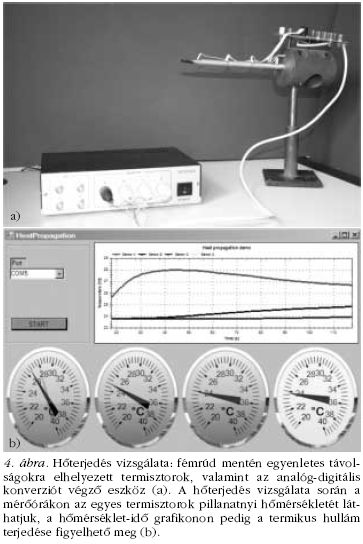
Virtuális műszerünk (4.b ábra) segítségével követhetjük
a termikus hullám terjedését. A
hőmérséklet-idő grafikonon mind a négy termisztor
hőmérséklet-változása nyomon követhető; az egyes termisztorokhoz
kapcsolt mérőórákon pedig megfigyelhetjük
az egyes pontok hőmérsékletének maximumát,
mivel ezeket az adott mérés során az órák
megőrzik.
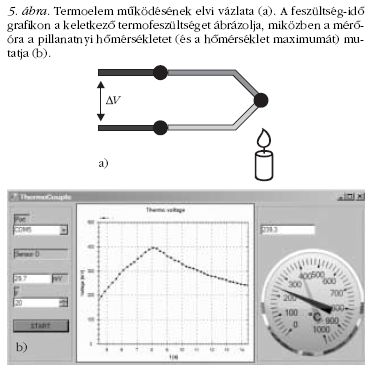
Termoelem működésének bemutatása
A termoelemek két különböző anyagú, egyik végükön
összeforrasztott (összehegesztett, esetleg csak erősen
összecsavart) drótból állnak. Az érintkezési pont a termoelem
úgynevezett „érzékelőpontja”. Ha a szabadon
maradt két huzalvéget galvanométerhez vagy digitális feszültségmérő
műszerhez csatlakoztatjuk, majd a fémesen
érintkező drótvégeket (az érzékelő pontot) megmelegítjük,
a műszer feszültséget jelez (5.a ábra). A jelzett termofeszültség
hőmérsékletfüggő. A szenzor érzékenysége
10-40 µV/K, ugyanakkor széles hőmérsékleti tartományban
alkalmazható: a -100 °C és +1000 °C közötti
intervallumon mérhetünk vele.

A digitális jelet feldolgozva nyomon követhetjük a
feszültség és a hőmérséklet időbeli változását (5.b ábra),
előbbit a grafikonon, utóbbit pedig a mérőórán.
Meteorológiai állomás
Könnyedén készíthetünk olyan eszközt is, ami nem
csak a fizikaórákon használható. Földrajztanítás során
is bemutatható az időjárás-állomás, amelyhez termisztor,
nyomásérzékelő és páratartalom-érzékelő (6.a ábra)
szükséges. Az eszközzel a közvetlen környezetet
vizsgáljuk, ezzel fokozott motiváló hatást érhetünk
el, csökkenthetjük a gyermekek tudatában meglévő
távolságot az iskolai tananyag és a hétköznapi valóság
között.
Mérés közben a monitoron folyamatosan megfigyelhető
a hőmérséklet, a légnyomás és a páratartalom
pillanatnyi értéke (6.b ábra).
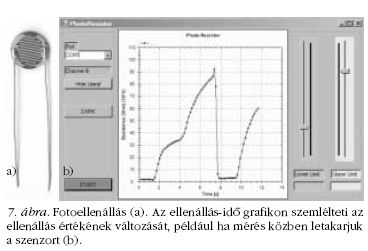
Fotoellenállás vizsgálata
A fotoellenállás olyan félvezetőből készült eszköz,
amely alkalmas a fény érzékelésére (7.a ábra). A
beeső fény változtatja az ellenállás értékét, a változás
elektromos jellé alakítható.
A mérés során ellenállás-idő grafikont vehetünk fel
(7.b ábra), amelyen jól látszanak a változások, például,
ha mérés közben változik a megvilágító fény intenzitása.
Műszerünk lehetőséget ad arra, hogy az ellenállás értékének
alsó és felső határt állítsunk be. Ha a megadott
intervallumon kívül esik a mért érték, akkor a program
ezt egy „világos”/”sötét” gomb megjelenítésével jelzi.
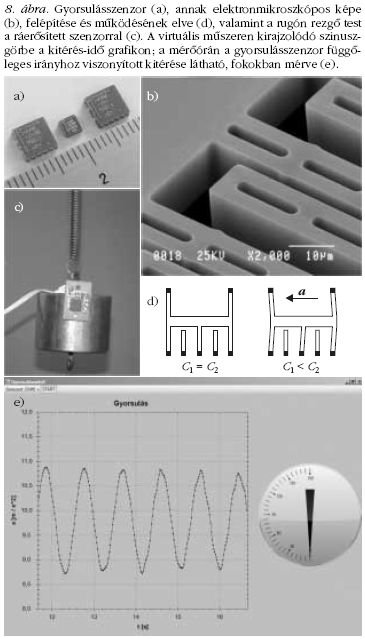
Rugón rezgő test mozgásának kvantitatív vizsgálata
gyorsulásmérő segítségével
A gyorsulásmérő (8.a ábra) alapelve egy rugóra erősített,
szeizmikus tömeg (8.c ábra) elmozdulásának elektromos
jellé alakítása. Kapacitív érzékelés esetén a tömeggel
szemben egy síklap található; a tömeg alja és a síklap
egy kondenzátor két fegyverzetét alkotják (8.b, d ábra),
amelynek kapacitása függ a fegyverzetek távolságától.
Ha a kitérés pontosan függőleges, akkor a kitérés-idő
függvény szinuszos; oldalirányú mozgáskomponensek
esetén megfigyelhető a csatolás a rezgés és az ingaszerű
lengés között. A monitoron a gyorsulás-idő grafikon melletti
mérőórán nyomon követhető a rezgő test mozgásának
eltérése a függőleges iránytól (8.e ábra).
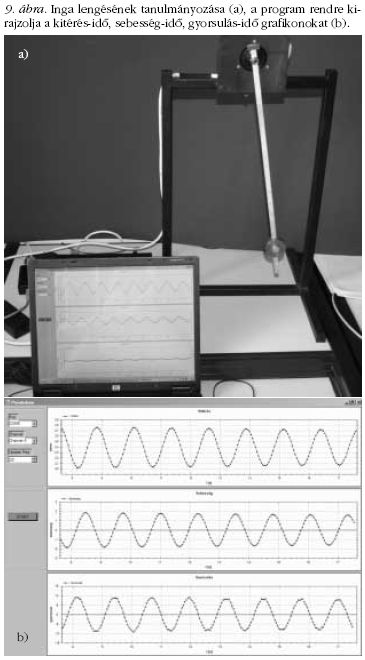
Ingamozgás tanulmányozása
Az ingához könnyű mozgású forgó-potenciométert illesztve
az elfordulás változó feszültségosztást eredményez
(9.a ábra). Ezzel a szögmérést feszültségmérésre
vezettük vissza. A számítógép képernyőjén (9.b ábra)
a mérési adatok alapján megjelenített kitérésidő
függvényen túl a sebesség-idő és a gyorsulás-idő
grafikon is kirajzoltatható (numerikus deriválás alkalmazásával).
A módszer segítségével gyorsan kapunk
pontos adatokat, amelyek az ingamozgás tulajdonságainak
vizsgálatát megkönnyítik.
<>
Az elkészült kísérleti eszközök alkalmasak arra, hogy
tanári mérőkísérletként, csoportos tanulói kísérletként,
vagy igényes mérési gyakorlaton használjuk fel
az órákon, szakkörökön. Alkalmazásukkal a kevésbé
motivált diákok érdeklődését is felkelthetjük a fizika
iránt, az egyre csökkenő tanítási időben is valódi kísérletet
mutathatunk be szimuláció helyett. A kiemelkedő
képességű tanulókat a kísérletek továbbfejlesztésébe
is bevonhatjuk.
A virtuális méréstechnika alkalmazásával lehetőség
nyílik a természettudományos tanári munkaközösség
és az informatikát tanító tanárok együttműködésére
is. Az érdeklődő diákok maguk is fejleszthetik a kísérleteket,
ezáltal összekapcsolhatják a különböző tanórákon
megszerzett tudásukat.
A virtuális méréstechnikát alkalmazó, kísérletező tanár
az alábbi kompetencia-elvárásoknak is megfelel:
- azoknak a kompetenciáknak a fejlesztése a tanulókban/
hallgatókban, amelyek a tudás alapú társadalom
számára szükségesek. Nyitottá válnak az új ismeretek
megszerzésére;
- az új kompetenciák (pl. számítógépes kompetencia)
fejlesztésének és a tantárgyi tanulásnak az
összekapcsolása;
- a hatékony tanulási környezet és a tanulási folyamatok
támogató légkörének megteremtése;
- az IKT (info-kommunikációs technológiák) integrálása
a különböző tanulási helyzetekbe és a szakmai
tevékenység egészébe;
- csapatmunkában történő együttműködés a tanulók/
hallgatók ugyanazon csoportjaiban dolgozó más
tanárokkal/oktatókkal, illetve egyéb szakemberekkel;
- a tanár kezdeményező szerepet vállal saját szakmai
fejlődésének irányításában [4].
A Szegedi Tudományegyetemen tanuló fizikatanár-
szakos hallgatók a szakmódszertani laboratórium
során megismerik a virtuális méréstechnika alapjait, a
mérőeszközöket és a programokat is. A gyakorlatokon
tapasztalható érdeklődés arra inspirál bennünket,
hogy minél szélesebb körben megismertessük a
kifejlesztett méréseket, és további eszközöket tervezzünk.
Virtuális méréstechnikáról, a kifejlesztett mérőprogramokról,
szenzorokról további információ (irodalom,
letölthető anyagok) találhatók a következő címen:
http://www.noise.physx.u-szeged.hu/VirtualM/default.htm
- Az érettségi vizsga részletes követelményeiről szóló 40/2002.
(V.24) OM rendelet (http://www.okm.gov.hu)
- Gingl Zoltán, Kántor Zoltán: Virtuális méréstechnika a kísérletező
oktatásban. II. Országos Neveléstudományi Konferencia
2002. MTA Pedagógiai Bizottsága, 348 oldal
- Török Miklós: Elektronika. JATEPress (2000) 153., 155. o.
- Nagy Mária: Új kompetenciaelvárások és új képzési gyakorlatok
a tanári szakmában. Új Pedagógiai Szemle 2004. április-május