Fizikai Szemle 2008/9. 302.o.
BOLYAI JÁNOS EGYIK LEGHOSSZABB FIZIKA TÁRGYÚ
KÉZIRATÁRÓL
Oláh-Gál Róbert
Babes¸-Bolyai Egyetem, Matematikai-Informatikai Kar,
Csíkszeredai Tagozat, Informatikai Rendszerek Tanszék
A Fizikai Szemlében Gábos Zoltán professzor értékes
cikkeket közölt a Bolyai-Lobacsevszkij-féle gravitációs
törvényről [1, 2]. Bolyairól ezt írja:
“....Egy 1835-ös keltezésű kéziratában a nemeuklideszi
alapra helyezett mechanika kidolgozását szorgalmazta.
Első lépésként egy új, nemnewtoni gravitációs
törvényt adott. Az M tömegű test által, tőle r távolságban
lévő, m tömegű testre gyakorolt centrális
erő radiális komponensére a newtoni elmélet az
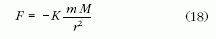
képletet adta. A (18) jobb oldalán szereplő törtet 4π-
vel bővítve a nevezőben, a gömbfelszínre érvényes
A megtalált Bolyai-kéziratok egy lapja [6]
euklideszi kifejezés jelentkezik. A Bolyai-Lobacsevszkij-
geometria a gömbfelszínre a
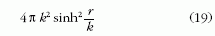
kifejezést adta. Bolyai erre alapozott, amikor (18)-at az
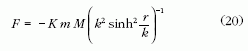
erőképlettel helyettesítette. Bolyai világában k-nak a
természetes hosszegység szerepet szánta, és a valóságnak
megfelelő k érték megadását a megoldandó
feladatok körébe sorolta.
Bolyai János erőtörvényével fél évszázaddal előzte
meg korát. P. Stäckel, aki még láthatta a törvényt tartalmazó
kéziratot, az 1903-ban közölt A többméretű sokaságok
mechanikájáról című dolgozatában a következőket
írta: »Érdekes, hogy egy bolygó mozgását a központi
test körül Killing (1885-ben) ugyancsak a Bolyai Jánostól
föltételezett vonzási törvény mellett discutálta.«
Később Stäckel 1914-ben kiadott Bolyai Farkas és Bolyai
János geometriai vizsgálatai című könyvében azt
is jelezte, hogy Lobacsevszkij Bolyaival csaknem egy
időben szintén megállapította a (20) alatti törvényt,
amelyet a Kazanyi Egyetem Tudományos Közleményeiben
közölt. Ezért (20)-at joggal nevezhetjük Bolyai-
Lobacsevszkij-féle gravitációs törvénynek.”
A fenti közleményben Gábos professzor Paul Stäckel
könyvére alapozva azt írja, hogy Bolyai János eredeti
kéziratának nyoma veszett.
Szerencsére a kézirat megvan és igazolható, hogy
Bolyai János vizsgálat alá vett egy újgravitációs törvényt,
amit Gábos professzor Bolyai-Lobacsevszkijféle
gravitációs törvénynek nevez [1, 2]. Feltételezhetően
ennek a kéziratnak lehetett egy letisztázott változata,
amit megismert Paul Stäckel, illetve valamelyik
munkatársa, aki neki magyarról németre fordította az
iratot, illetve azt a részét, amit ki tudott betűzni.
Ugyanis ezt a fajta kéziratot az 1900-as évek elején
még nemigen olvasták ki. Erre az a bizonyíték, hogy
nem említi egyetlen egy Bolyai-kutató sem, hogy Bolyai
Jánost foglalkoztatta Boskovich elmélete.
Íme egy idézet az általunk újra megtalált Bolyai-kéziratból:
“azon von-törvény: mi-szerént a' von-erő úgy nő:
mint a' távval irott kör fölfordultja, vagyis visszáson
úgy mint a' táv-kör; másik eset pedig az: mikor - föltéve,
mit még nem vizsgáltam meg: hogy S-ben1 is
 ban2
van az iminti törvény mellett, szerént akarmely
egy-köz-centerű gömb-lepek,3 sőt sphaerors-lepek
által is, határozott testen belüli szer4 akár - az oly
hatás szerénti törvény: melyet külső mindenütt egytömű
(egytömegű?) gömbök egyenlő, 's külszineket,
rajtuk lévő hasonló gömbökre gyakorolnak - mely
kerdvény? Hogy egyezik-e az erőnek a' távval vagy-is
inkább a' táv-körreli növelésével. (Csakugyan általánosan
kell a von-erővel bánni, 's q = fx5 szerént úgy,
hogy mágnesi, 's bármely lehető más testekre is legyen
alkalmazható). (függetlenül szólva az Euklidesz
XI Axiomától)”
ban2
van az iminti törvény mellett, szerént akarmely
egy-köz-centerű gömb-lepek,3 sőt sphaerors-lepek
által is, határozott testen belüli szer4 akár - az oly
hatás szerénti törvény: melyet külső mindenütt egytömű
(egytömegű?) gömbök egyenlő, 's külszineket,
rajtuk lévő hasonló gömbökre gyakorolnak - mely
kerdvény? Hogy egyezik-e az erőnek a' távval vagy-is
inkább a' táv-körreli növelésével. (Csakugyan általánosan
kell a von-erővel bánni, 's q = fx5 szerént úgy,
hogy mágnesi, 's bármely lehető más testekre is legyen
alkalmazható). (függetlenül szólva az Euklidesz
XI Axiomától)”

Bármennyire is nehézkes a szöveg, ennek a képletszerű
megfejtése az, amit Gábos professzor közölt
[2]-ben.
Még két dolgot szeretnénk kiemelni a kéziratból.
Nagyon érdekes gondolat az alábbi:
“Csak Atyámtól hallám gyermek koromban, hogy
egy szerben például az éppen tanult, közben kezében
volt krétában annyi erő lehet, hogy tán egy bihal sem
volna képes meggyőzni, bírni vele.”
Tehát az anyagban, egy kis krétában annyi erő,
(amit ma energiának mondunk) van, amit egy bivaly
sem volna képes kifejteni. Véleményünk szerint
ennek egyik értelmezése a Boskovich-féle atomelméletben
keresendő. A kéziratban kétszer is történik
utalás Ruder J. Boskovichra. Ismeretes, hogy Faraday
is elfogadta Boškovic´ atomelméletét, amely szerint az
atomok közötti kötéseket csak óriási erővel lehet szétszakítani.
Viszont a Bolyai-kutatók eddig nem tudták,
nem közölték, hogy mind a két Bolyai olvasta Boskovich
Teleki-tékában is meglévő műveit. A Teleki-téka
három Boskovich-művel is büszkélkedhet [3-5]. Rendkívül
modern tudományos tájékozódásról tesz ez tanúbizonyságot.
Boskovichot a modern fizikatörténetben
és atomkorszak leírásában is alig említik.
És végül: véleményünk szerint igen érdekes vízió a
végtelen sebességű anyagi pont gondolata, amely
mégis véges távolságot tesz meg. Egy ilyen fizikai
jelenség a Bolyai-geometriának is egy elképzelhető
fizikai alkalmazásra adna lehetőséget.
“NB. Képzelhet oly erő, 's mozgás is áll: hogy egy
üd-pontkor6 (ha nem is az egyik szer ' súlypontjában)
az egyik szer söbe7 éppen = végtelen legyen azután
perse rögtön hasonló törvény szerént leapadóvá. És
már koránt sem ismervén minden szerek vonerejét:
nem is állíthatjuk: hogy nincs a' természetben de
csak némely üd-pontkor, éppen végtelen söbű mozgás;
melynek azonban perse még is csak véges út az
eredménye.
NB. Csepegő 's légfolyó, 's rugonyos szereknek
hason esetben (körülmények között) vizsgája ezután
's így lehet bárhány több hasonló szabályú szer
ugyan-azon tengely körül helyezve: meghatározni az
egész mozgást bármely föltett vontörvény mellett,
szerént.”
Természetesen ezenkívül sok-sok fizikai ötlet, kísérlet
és eszmefuttatás szerepel a közel tízoldalas kéziratban,
s a jövőben igyekszünk majd annak teljes
szövegét is közreadni.
A címben, szándékosan “egyik leghosszabb” és nem
a “leghosszabb fizikai tárgyú Bolyai-féle eszmefuttatás”
szerepel, mert még sok meglepetést hozhat a Bolyai-kéziratok
megfejtése. Bolyai János kéziratai nehéz olvasmányok.
Halmozza a jelzőket és ötleteket, gondolatmenete
is csapongó, valószínűleg a kezeírása ritkán
volt összhangban éles eszének száguldásával. De a legtöbb,
matematikát tartalmazó kéziratára ez jellemző.
Irodalom
- Gábos Zoltán: A Bolyai-Lobacsevszkij-féle gravitációs törvény.
Fizikai Szemle 50/1 (2000) 13.
- Gábos Zoltán: A klasszikus gravitációelméletről. Fizikai Szemle
54/12 (2004) 397-401.
- Boscovich, Joseph: De Solis et Luna. Venetiis, 1761.
- Boscovich, Joseph: Abhandlung von den verbesserten dioptrischen
Fernröhren. Wien, 1765.
- Boscovich, Joseph: Trigonometria plana et sphaerica. Collig.
cum: Tacquet, Andreas: Elementa Geometria. Patavii, 1761.
- Teleki-Bolyai Könyvtár, Bolyai Gyűjtemény, BJ 1337/1, 1v, 1338/1,
1v, 2, 2v, 1339/ 1, 1v, 1339/2, 2v.
__________________
1 S-ben, vagyis a Bolyai-geometriában
2 -ban = megfeleltetésben van
3 gömb-lepek = gömbfelszín
4 szer = anyag
5 Mai jelöléssel: q = f (x)
6 üd-pont = időpont
7 söbe = sebessége
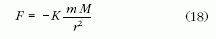
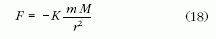
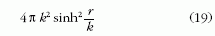
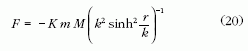
 ban2
van az iminti törvény mellett, szerént akarmely
egy-köz-centerű gömb-lepek,3 sőt sphaerors-lepek
által is, határozott testen belüli szer4 akár - az oly
hatás szerénti törvény: melyet külső mindenütt egytömű
(egytömegű?) gömbök egyenlő, 's külszineket,
rajtuk lévő hasonló gömbökre gyakorolnak - mely
kerdvény? Hogy egyezik-e az erőnek a' távval vagy-is
inkább a' táv-körreli növelésével. (Csakugyan általánosan
kell a von-erővel bánni, 's q = fx5 szerént úgy,
hogy mágnesi, 's bármely lehető más testekre is legyen
alkalmazható). (függetlenül szólva az Euklidesz
XI Axiomától)”
ban2
van az iminti törvény mellett, szerént akarmely
egy-köz-centerű gömb-lepek,3 sőt sphaerors-lepek
által is, határozott testen belüli szer4 akár - az oly
hatás szerénti törvény: melyet külső mindenütt egytömű
(egytömegű?) gömbök egyenlő, 's külszineket,
rajtuk lévő hasonló gömbökre gyakorolnak - mely
kerdvény? Hogy egyezik-e az erőnek a' távval vagy-is
inkább a' táv-körreli növelésével. (Csakugyan általánosan
kell a von-erővel bánni, 's q = fx5 szerént úgy,
hogy mágnesi, 's bármely lehető más testekre is legyen
alkalmazható). (függetlenül szólva az Euklidesz
XI Axiomától)”
