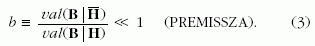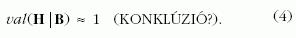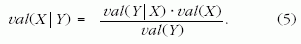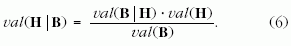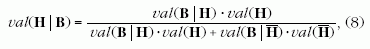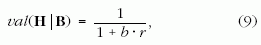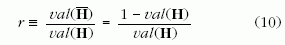Fizikai Szemle 2008/10. 321.o.
AZ ANTROPIKUS ELVRŐL
Hraskó Péter
PTE Elméleti Fizika Tanszék
Az antropikus elv et nagyon sok változatban fogalmazták
már meg, de a lényeget tekintve ezek mind
két alapforma változatai. A gyenge antropikus elv
abban foglalható össze, hogy az élet létezése feltételeket
ró az Univerzumfejlődését leíró modellekre.
Az erős antropikus elv pedig azt állítja, hogy ezek a
feltételek olyan szűk tűréshatárok közé szorítják a
különböző fizikai állandók (finomszerkezeti állandó,
nukleontömeg stb.) értékét, hogy egy ilyen Univerzum
semmiképpen sem lehet a "véletlen” terméke,
hanemcsakis valamilyen "intelligens tervezés” eredményeként
jöhetett létre, amelynek célja az élet feltételeinek
a biztosítása volt. Elég nyilvánvaló, hogy a
gyenge elv ugyan igaz, de lapos közhely, amellyel
nemérdem es foglalkozni. Az erős elv azonban rejtett
érvelési hibát (körkörösséget) tartalmaz, és ezt érdemes
feltárni.1
Jelöljük H-val azt a hipotézist, hogy a világ intelligens
tervezés eredménye, B-vel pedig a bizonyítékok
halmazát, vagyis a fizikai állandók konkrét értékeit (a
mérési hibáikkal együtt). Ezeket ugyan csak erős
fenntartással lehet "bizonyítéknak” tekinteni, mert a
kozmológiáról és az életről még túl keveset tudunk
ahhoz, hogy bizonyosan megállapíthassuk: A fizikai
állandóknak csakis a ma ismert értéke mellett lehetséges
az élet létrejötte a Világegyetemben. Tegyük
azonban félre a fenntartásainkat és tekintsük B-t a H
bizonyítékának.
Az erős antropikus elv két premisszából indul ki.
Az első az, hogy ha a Világegyetemnem intelligens
tervezettség következményeként jött létre, akkor nagyon
valószínűtlen, hogy a fizikai paraméterek pont
olyanok, amilyeneknek megismertük őket. Matematikailag
ezt a val (X|Y) függvény segítségével fejezhetjük
ki, amely X valószínűségével egyenlő az Y feltétel
teljesülése mellett:
A 
szimbólum itt a H ellentétét jelenti, vagyis azt a
hipotézist, hogy a világ nemvalam ilyen intelligens
tervezettség eredménye.
A második premissza az, hogy intelligens tervezettség
esetén viszont szükségképpen a ma ismert paraméterekkel
rendelkező világ jött létre, hiszen a tervezés
célja az élet feltételeinek a biztosítása volt. Matematikailag
ezt a
val (B | H) = 1 (2)
képlet fejezi hűen ki. Alább a képleteinkben az (1) és
a (2) valószínűségnek csak a hányadosa lép majd fel,
ezért a két premisszát egyetlen premisszába tömöríthetjük:
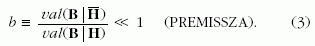
Ilyen típusú hányados gyakran fordul elő a matematikai
statisztikában, ahol Bayes-faktornak vagy likelihood-
aránynak hívják.
Az elv konklúziója az, hogy a bizonyítékok alapján
az intelligens tervezettség szinte bizonyos, a valószínűsége
gyakorlatilag 1-gyel egyenlő:
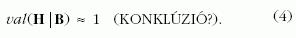
A kérdés az, hogy következik-e ez a konklúzió a
premisszából. Ha összehasonlítjuk a matematikai
alakjukat azt látjuk, hogy a premisszában szereplő
feltételes valószínűségeknek az első argumentuma a
bizonyíték, a második a hipotézis, a konklúzióban
szereplő valószínűségben pedig a sorrend fordított.
Ezért ha a konklúziót matematikailag ki akarjuk fejezni
a premisszán keresztül, a Bayes-formulát2 kell
használnunk, amely a következő:
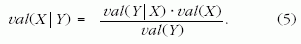
Az X és az Y lehet bármilyen esemény vagy kijelentés.
Ennek alapján
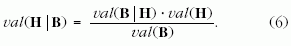
A képletben szereplő egyargumentumú val (X) az X
feltétel nélküli (abszolút) valószínűsége, speciálisan
val (B) a bizonyítékoknak (a fizikai állandók megfigyelt
értékének) az abszolút valószínűsége. A teljes
valószínűség tételének felhasználásával ez felírható a
következő formában is:
ahol val (H) annak valószínűsége, hogy a világ intelligens
tervezettség eredménye, a val (H) pedig annak
valószínűsége, hogy nemaz. Ez a két lehetőség egymást
kizárja, több lehetőség pedig nincs, ezért
val (H)+val (H) = 1. A (7) a B valószínűségét a két
lehetőségre vonatkozó valószínűségek súlyozott öszszegeként
állítja elő.
Helyettesítsük (7)-et (6) nevezőjébe:
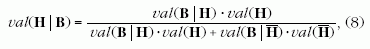
és ezután a tört számlálóját és nevezőjét osszuk el a
val (B | H) · val (H)
szorzattal:
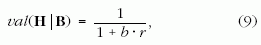
ahol
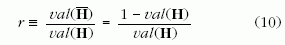
az úgynevezett bázisarány.
A (9) képlet bal oldalán a (4) konklúzióban szereplő
feltételes valószínűség áll, míg a jobb oldalon a b
Bayes-faktor a (3) premisszában szerepel. Ez a képlet
tehát alkalmas arra, hogy megállapíthassuk, következik-e
a premisszából a konklúzió.
Először feledkezzünk el a (9) nevezőjében r-ről. A
tört ekkor 1/(1+b). A premissza szerint b << 1, ezért
val (H|B) ≈ 1. Ez valóban azonos az erős antropikus
elv konklúziójával. Az r jelenléte azonban drámaian
megváltoztatja a helyzetet: ahhoz, hogy kiszámíthassuk
a bennünket érdeklő val (H|B)-t, a (10) következtében
már előzetesen ismernünk kell annak val (H)
valószínűségét, hogy a világ intelligens tervezés eredménye.
Ebből nyilvánvaló, hogy az erős antropikus
elv valóban körkörös érvelésen alapul.
A val (H) valószínűségnek kétféle értelmezése lehetséges,
egy objektív és egy szubjektív. Az objektív felfogás
szerint a H vagy igaz vagy hamis, ezért val (H) vagy
1 vagy 0. Az első esetben (10) szerint r = 0, (9) alapján
pedig val (H|B) = 1, ahogy azt az erős antropikus elv
sugallja. Azonban ebből egyáltalán nemvonható le az a
következtetés, hogy akkor tehát a világ intelligens tervezés
eredménye, mert ezt a bizonyításban már kihasználtuk
azzal, hogy val (H)-t 1-nek tekintettük - ezért
körkörös ez az elv. A második esetben teljesen hasonlóan
a val (H|B) = 0 eredményre jutunk, de a körkörösség
miatt ebből szintén nem következik, hogy a világ
intelligens tervezés nélkül jött létre.
A másik lehetőség az, hogy a val (H)-n azt értjük,
hogy valaki szubjektíven mennyire tartja valószínűnek
az intelligens tervezettséget: ha egyáltalán nem hisz
benne, akkor 0-nak választja, ha biztos benne, akkor
1-nek, ha pedig nem tud dönteni, akkor a bizonytalanságának
a mértékét a (0,1) intervallumba eső megfelelő
számmal fejezi ki. Minél jobban hisz valaki abban,
hogy a világ intelligens tervezettség következtében
jött létre, annál nagyobbnak választja val (H)-t,
annál kisebb lesz az r, a (9) szerint annál nagyobb
val (H|B) értékre jut, ezért (ha logikusan gondolkozik)
annál inkább vallja, hogy a fizikai állandók tapasztalt
értékei az intelligens tervezettséget bizonyítják.
Ennyi következik az erős antropikus elv premisszáiból,
semmivel se több.
____________________
1 Az alább következő gondolatmenettel kapcsolatban nyomatékosan
az olvasó figyelmébe ajánlom Pólya György A plauzibilis következtetés
elmélete. A matematikai gondolkodás művészete II. (Gondolat,
1989) könyvének XV. fejezetét.
2 Ezt a képletet úgy lehet megkapni, hogy a feltételes valószínűségek
val(X|Y) = val (X, Y)/val(Y) és val (Y|X) = val (X, Y)/val(X)
kifejezéseiből kizárjuk val (X, Y)-t, amely az X és az Y együttes előfordulási
valószínűsége.