Fizikai Szemle 2008/10. 347.o.
A XVIII. ÖVEGES JÓZSEF FIZIKAVERSENY
ORSZÁGOS DÖNTŐJE
Juhász Nándor
Szeged, Rókusi Általános Iskola
Ősz György
Ács, Jókai Mór Általános Iskola
Vida József
Eger, Eszterházy Károly Főiskola
A verseny krónikája
2008. május 23.
A XVIII. Öveges József Fizikaverseny országos
döntőjének idén is - az alapításának 100. évfordulóját
ünneplő, Pro Urbe-díj jal kitüntetett - győri Kazinczy
Ferenc Gimnázium és Kollégium adott otthont. A sikeres
rendezésben jelentős szerepet vállaltak, mint
társrendezők: Győr-Moson-Sopron Megye Közgyűlése,
Győr Megyei Jogú Város Polgármesteri Hivatala,
Győr-Moson-Sopron Megyei Pedagógiai Intézet, Kazinczy
Ferenc Gimnázium igazgatósága.
A városháza impozáns dísztermében megnyitó ünnepéllyel
kezdetét vette a három napos, országos
fizikaverseny. A megjelenteket Ősz György a szakcsoport
vezetőségének tagja, a versenybizottság titkára
köszöntötte. Kádár György, az ELFT főtitkára köszöntőjében
szólt a fizika szépségéről, a megismerés határtalanságáról,
az emberi gondolkodásban, tudásban
rejlő hatalmas energiák jelentőségéről és a jövő természetkutatói
előtt álló feladatokról.
Göncz Kinga (édesanyjának nagybátyja volt Öveges
József) a család képviseletében köszöntötte a versenyzőket.
A természettudományok azon kiemelkedően
fontos szerepét hangsúlyozta, amit a jövőben
betölthetnek hazánknak az európai fejlett országok
szintjére való felzárkózásában.
A versenyzők és kísérőik a megnyitó ünnepélyt
követően városnézésen vettek részt.
2008. május 24.
A délelőtt folyamán teszt jellegű feladatsort, és két
számításos feladatot kellett megoldani. Délután önállóan
elvégzett mérő kísérlet, egy bemutatott kísérlet
elemzése és fizikatörténeti keresztrejtvény megoldása
következett.
A döntő feladatsorának összeállításában Vida József
vezetésével Csákány Antalné, Kövesdi Katalin, Hóbor
Sándor, Horváthné Fazekas Erika, Pápai Gyuláné,
Wöller László, Gyimesi Éva és Pál Zoltán vett részt. A
versenybizottság titkárát, Ősz Györgyöt Fülöp Viktorné,
Poócza József és Juhász Nándor segítették. Ők szervezték
a döntőt és a hozzá kapcsolódó rendezvényeket.
A zsűri elnöke Hadházy Tibor, tagjai Maráz Lászlóné,
Pöltl János, Nickházy Lászlóné, Kleizerné Kocsis
Mária, Horváthné Fazekas Erika, Lévainé Kovács
Róza, Pál Zoltán, Slezák Zsolt voltak. A zsűri ellenőrei
Szénási Istvánné és Krakó László voltak.
A verseny három napja alatt felügyelői és szervező
feladatokat láttak el: Horváthné Perger Zsuzsanna,
Antoni Istvánné, Vidáné Papp Csilla, Várhegyi
Lászlóné, Wernerné Pöheim Judit, Wöller Lászlóné.

A délelőtt folyamán a kísérőtanároknak Kiss Gyula,
az ELFT Általános Iskolai Oktatási Szakcsoportjának
elnöke adott tájékoztatást az Öveges-verseny eddigi
fordulóinak szervezési gondjairól, eredményeiről. Ezt
követően a felkészítő tanárokkal eszmecserét folytattak
a fizikatanítás jelenéről, jövőjéről és a tehetséggondozás
lehetőségeiről.
Még a vacsora előtt a tanulók és kísérőik átsétáltak
a városi Tűzoltóságra, ahol Mészáros Péter tanár úr
(Győr, Krúdy Gimnázium) szervezésében tanúi lehettek
a vízzel bemutatott Torricelli-kísérletnek, amit egy
bátor versenyző lány közreműködésével hajtottak
végre a tűzoltóautó több, mint 10 méter magasra felemelt
kosarában.
Vacsora után kellően elcsigázva, de lankadatlan érdeklődéssel
vonultak át a versenyzők és kísérőik a
Révai Gimnázium dísztermébe, ahol Tóth Pál tanár úr
a FIZIBUSZ "vezetője” tartott kísérletekkel illusztrált
igen érdekes előadást. Köszönet érte az ELMŰ-nek és
az ÉMÁSZ-nak.
2008. május 25.
Vasárnap reggel fél kilenckor a városháza dísztermében
Horváthné Fazekas Erika, a szakcsoport vezetőségének
tagja vezette le az eredményhirdetést és
díjkiosztást. Sólyom Jenő akadémikus, az ELFT elnöke
és Ottófi Rudolf, Győr város alpolgármestere köszöntő
szavai után Vida József a versenybizottság nevében,
Hadházy Tibor a zsűri nevében elemezte, értékelte
a megoldásokat.

Eredmények, díjazottak
Az idei versenyen a zsűri a legjobb 33 versenyzőt díjazta
(77% feletti teljesítményt). 14-en dicséretben
részesültek, 12-en III. díjat, 6-an II. díjat, és egy tanuló
kapott I. díjat.
Az ELFT Általános Iskolai Szakcsoportja által erre a
célra alapított Öveges József Érem is már kilencedik éve,
hogy gazdára talált; a verseny első helyezettje, Bolgár
Dániel, aki 95 pontot ért el a maximális 100-ból, a PTE
Deák Ferenc Gyakorló Gimnázium és Általános Iskola
tanulója és felkészítő tanára, Sebestyén Klára kapták.
II. díjat kaptak
Galgóczi Gábor (89 pont), Radnóti Miklós Gimnázium,
Dunakeszi, felkészítő tanára: Tölgyesiné Irmes
Marianna
Tilk Bence (85), Felsővárosi Általános Iskola Balassi
Bálint Tagiskola, Eger, Kiss Gézáné
Vona István (85), Ráday Pál ÁMK, Harta, Eltiganiné L.
Eszter
Bozzai Dániel (85), Városmajori Gimnázium, Budapest,
Ábrám László, Jäger Csaba
Kertész Dávid (84), Munkácsy Mihály Általános Iskola,
Pápa, Megyeriné Borsó Éva
Sándor Tímea (84), Veres Péter Gimnázium, Budapest,
Csaba György, Erdősi Katalin
III. díjat kaptak
Kovács Gábor Ferenc (83), Árpád Gimnázium, Tatabánya,
Szabó József
Deák Norbert (83), Báthory István Elméleti Líceum,
Kolozsvár, Popa Márta
Suri Bálint (82), Széchenyi István Gimnázium, Sopron,
Czupy Judit
Vértesy Gáspár (82), Belvárosi Általános Iskola és
Alapfokú Művészetoktatási Intézmény, Dombóvár,
Embersitsné Bóta Éva
Szigeti Bertalan (82), Vetési Albert Gimnázium, Veszprém,
Kovács Ilona
Bacher Viktor (82), Liszt Ferenc ÁMK Általános és
Alapfokú Művészetoktatási Intézmény, Mecseknádasd,
Schwarcz Jánosné
Göncz Csaba András (82), Zrínyi Miklós Általános
Iskola, Nagykanizsa, Lelkes Andrásné
Bozsik Máté (81), Kodály Zoltán Általános Iskola,
Tatabánya, Plavecz Jánosné
Inhoff Gergő (81), Sztárai Mihály Gimnázium, Tolna,
Oberländer Sándorné
Romvári Petra (81), Váci Utcai Ének-zenei Általános
Iskola, Budapest, Hammer Mariann
Farkas Martin (80), Csány-Szedrey ÁMK Belvárosi
Tagiskola, Keszthely, Fölföldiné Katona Erika,
Farkas László
Szabó András (80), Petőfi Sándor Általános Iskola,
Vác, Detréné Kékesi Márta
Minden díjazott könyvcsomagot és az oktatási miniszter
által aláírt oklevelet kapott.
Életpályájukat lehet, hogy éppen a versenyekre
való felkészülés során alakuló világszemléletük, szorgalmuk,
sikerélményük és a beléjük táplált munkaszeretet,
tudománytisztelet határozza meg.
A verseny feladatsora
Tesztek
- A szoba asztalára két egyforma, vízzel félig telt
üvegpoharat tettünk. Az egyik pohár kívülről, a másik
belülről párásodik be. Hogyan lehetséges ez?
- ) Az egyik pohárban forró, a másikban jéghideg
víz van. A meleg vizet tartalmazó pohár belülről, a
hideg vizet tartalmazó pedig kívülről párásodik be.
- ) A tapasztalatok oka az, hogy mindkét pohárban
szobahőmérsékletű víz van, de a két pohár falvastagsága
különböző.
- ) Az egyik poharat a hideg erkélyről, a másikat a
meleg sütőből hoztuk be. Ez utóbbi párásodik be kívülről.
- ) A két pohár különböző méretű. A nagyobb méretű
pohár belülről, a kisebbik kívülről párásodik be.
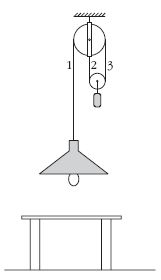 Egy
cipőjavító műhelyben a cipész munkaasztalát
megvilágító lámpatestet két csigából álló szerkezettel
lehet lejjebb engedni, vagy
feljebb emelni. A rendszer
bármely helyzetben egyensúlyban
van. Minősítsd az
állításokat, ha a mozgócsiga
tömege elhanyagolható az
ellensúly tömegéhez képest!
Egy
cipőjavító műhelyben a cipész munkaasztalát
megvilágító lámpatestet két csigából álló szerkezettel
lehet lejjebb engedni, vagy
feljebb emelni. A rendszer
bármely helyzetben egyensúlyban
van. Minősítsd az
állításokat, ha a mozgócsiga
tömege elhanyagolható az
ellensúly tömegéhez képest!
- ) Mindhárom zsinórt
ugyanakkora erő feszíti, így
az ellensúly kétszer nehezebb
a lámpatestnél.
- ) A mozgócsiga mindkét
zsinórját ugyanakkora erő
feszíti, ezért a lámpatest fele
akkora súlyú, mint az ellensúly.
- ) Az 1-es és a 3-as zsinórt ugyanakkora erő feszíti.
Ugyanez mondható el a 2-es és a 3-as zsinórról is.
Ennek értelmében az ellensúly és a lámpatest tömegaránya
2:1.
- ) Az ellensúlyt két zsinór tartja, a lámpát csak egy.
Emiatt lehet a lámpatest harmad annyi súlyú, mint az
ellensúly.
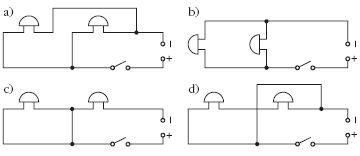
- Egy ház előszobájában és a házhoz közeli melléképületben
lévő műhelyben is elhelyeztek egy-egy elektromos
csengőt. Az alábbi kapcsolási rajzok közül melyik
mutatja helyesen azt, hogy a kapunál levő nyomógombbal
egyidejűleg működtethető mindkét csengő?
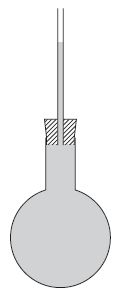 Egy
lombikot 10 °C hőmérsékletű
vízzel teletöltöttünk, majd lezártuk
egy olyan dugóval, amelynek a
közepét átfúrtuk. A furaton keresztüldugtunk
egy szorosan beleilleszkedő,
vékony üvegcsövet. Az
üvegcsőben a víz szintje - az ábrának
megfelelően - felemelkedett.
Mi történik a csőben levő víz szintjével,
ha a lombikot egy nagy kád jeges
vízbe tesszük, és megvárjuk, míg
a lombikban levő víz hőmérséklete
közel 0 °C-sá válik?
Egy
lombikot 10 °C hőmérsékletű
vízzel teletöltöttünk, majd lezártuk
egy olyan dugóval, amelynek a
közepét átfúrtuk. A furaton keresztüldugtunk
egy szorosan beleilleszkedő,
vékony üvegcsövet. Az
üvegcsőben a víz szintje - az ábrának
megfelelően - felemelkedett.
Mi történik a csőben levő víz szintjével,
ha a lombikot egy nagy kád jeges
vízbe tesszük, és megvárjuk, míg
a lombikban levő víz hőmérséklete
közel 0 °C-sá válik?
- ) Az üvegcsőben rövid ideig
emelkedik a víz szintje, majd süllyed,
és megállapodik a kezdeti szint
alatti magasságban.
- ) Az üvegcsőben folyamatosan csökken a víz
szintje mindaddig, amíg a lombikban is közel 0 °C
lesz a vízhőmérséklet.
- ) Az üvegcsőben először nő a víz szintje, majd
csökkenni kezd. Egy idő múlva ismét nő a vízszint,
mindaddig, amíg a lombikban lévő víz hőmérséklete
el nem éri a közel 0 °C-ot.
- ) Az üvegcsőben folyamatosan emelkedik a vízszint.
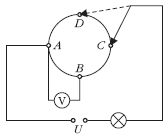
- Egy
nagy ellenállású króm-nikkel vezetődarabból
gyűrűt formálunk az alábbi rajzon látható módon,
majd az A és C pontjával áramkörbe
kapcsoljuk.
Ezt követően az eredetileg
C ponthoz kapcsolódó
érintkezőt áthelyezzük
a D pontba, a szaggatott
vonallal jelzettnek megfelelően.
Az érintkező áthelyezése után:
- ) Az izzó nagyobb fényerővel világít.
- ) A voltmérő nagyobb feszültséget mutat.
- ) A B és C pontok közti gyűrűrészen a teljesítmény
kisebb lesz.
- ) A CD gyűrűrész magasabb hőmérsékletű lesz,
mint az AD gyűrűrész.
- Hogyan érhető el 2 síktükör segítségével, hogy a
másodikról visszaverődő fénysugár párhuzamos legyen
az első tükörre beeső fénysugárral?
- ) A két síktükröt - tükröző felületükkel befelé -
egymásra merőlegesen úgy helyezzük el, hogy az első
tükörre eső fénysugár az első tükör síkjával 45°-os
szöget zárjon be.
- ) Tükröző felületükkel befelé, egymásra merőlegesen
elhelyezett két síktükör esetében a második
tükörről visszavert fénysugár mindig a beeső fénysugárral
párhuzamosan verődik vissza.
- ) A két síktükröt - tükröző felületükkel befelé -
egymással tetszőleges nagyságú tompaszöget bezáróan
helyezzük el. Ha a fénysugár az első tükörre 45°-os beesési
szögben érkezik, akkor a másodikról visszavert
fénysugár párhuzamos lesz az első tükörre érkezővel.
- ) Ha két síktükröt tükröző felületükkel egymással
párhuzamosan szembefordítunk, úgy, hogy az egyikre
tetszés szerinti szögben érkező fénysugár a visszaverődést
követően ráeshessen a másik tükörre, akkor
a második tükörről visszavert fénysugár párhuzamos
lesz az elsőre beesővel.
- Írd be az állítások előtti pontsorba az általad megfelelőnek
tartott ábra sorszámát!
.... Holdfogyatkozást észlelünk a Földön, Európában
nyár van.
.... Ausztráliában nyár van, a Föld bizonyos részein
teljes napfogyatkozást figyelhetnek meg.
.... A Föld a Nap és a Hold közé kerül, a déli féltekén
tél van.
.... Magyarországon, januári éjszakán holdfogyatkozásban
gyönyörködhetnek az emberek.

Értékelés
A tantervi témakörök mindegyikét reprezentálta
legalább egy tesztkérdés. Mindegyik feladat jó megoldásával
4, így összesen 28 pontot lehetett szerezni. A
legtöbb nehézséget az 5. a 6., és a 7. kérdés jelentette.
A 28 lehetséges pontot ketten érték el, a legkevesebb
pontot szerző résztvevő 32%-os eredményt ért el.
Mindössze két tanuló nem érte el az 50%-ot, 45%-
uk 75-86% között, 40%-uk viszont 90% felett teljesített.
A tanulók teszten elért átlaga kerekítve 84%.
Számításos feladatok
- Párhuzamosan kapcsolt 10 Ω és 20 Ω nagyságú ellenállások
áramkörében két 6 V feszültségű áramforrás
két különböző módon van bekötve (lásd az 1. és a
2. ábrát).
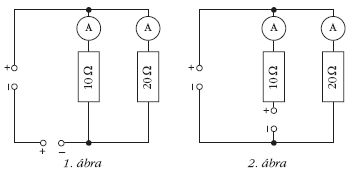
Határozd meg a négy mérőműszer által jelzett értéket!
Értékelés
Ezzel a feladattal 8 pontot lehetett szerezni. Megoldásában
4,7 átlagpontot értek el a versenyzők, ami
kerekítve 59%-os teljesítménynek felel meg. Hibátlanul
csak a tanulók 13%-a oldotta meg a feladatot. Kevesen
jöttek rá, hogy logikai következtetésekkel is el
lehet jutni a megoldáshoz.

Ez a feladat azért is okozott sokaknál problémát, mert
szembe kapcsolt telepekkel kapcsolatos feladatot keveset
oldottak meg. (Ilyen jellegű feladatot - legalábbis a
döntőig eljutottak - kellett, hogy lássanak.)
- Három azonos alapterületű, különböző anyagú
hengerről az alábbiakat tudjuk:
- térfogataik aránya: 1 : 2 : 3;
- a három henger átlagos sűrűsége 2566,67 kg/m3;
- az egyik henger rézből van, sűrűsége 8,9 kg/dm3;
- a legnagyobb térfogatú hengernek a legkisebb a
súlya;
- a három henger együtt, ha mindhárman teljesen víz
alatt vannak, 54 dm3 térfogatú vizet szorít ki egy vízzel
teli medencéből;
- a középmagas henger súlya 450 N;
Mekkora a legnagyobb térfogatú henger anyagának
a sűrűsége?
Értékelés
A zsűri várakozásaival szemben ennek a feladatnak
a megoldottsága lett a legmagasabb. A lehetséges 21
pontból 19,7-es átlagot értek el a versenyzők, ami
94%-os eredménynek felel meg. Összehasonlítva a
számításos (1) feladattal, megállapíthatjuk, hogy a
mechanikai problémák közel sem jelentenek akkora
nehézséget, mint az elektromosságtaniak.
Kísérletelemző feladat
Egy 600 és egy 1200 menetű elektromágnes erősségét
vizsgáljuk három egymást követő kísérletben.
Korábban megvizsgáltuk, és megállapítottuk, hogy
mindkét tekercs rézhuzalból van, továbbá azt, hogy a
600 menetű tekercs huzala vastagabb, mint az 1200
menetűé.

A három egymást követő kísérlet az alábbi volt:
Az első kísérletben a kísérletet bemutató tanár az
áramforrásra sorosan kapcsolt két elektromágnessel egy
vasszögeket tartalmazó tálcából vasszögeket emelt ki.
A második kísérletben egyszer kisebb, másszor
nagyobb erősségű árammal átfolyt tekercsekkel emelt
ki szögeket a tálcából.
A harmadik kísérletben párhuzamosan kapcsolta a
két elektromágnest, és most azokkal így emelt ki szögeket
a tálcából.
Az elektromágnesek által vonzott szögcsomókat az
asztalon egymástól elkülönített helyre rakta ki.
(A rávezető kérdéseket követően a versenyzőknek
arra kellett választ adni, hogy soros kapcsolásnál miért
a nagyobb menetszámú, párhuzamos kapcsolásnál
miért a kisebb menetszámú elektromágnes az erősebb.)
Értékelés
A tanulók teljesítményszintjének átlaga alig emelkedett
50% fölé, vagyis ennek a feladatnak a megoldottsága
átlagosnak mondható. Kiemelkedően jó
megoldást egyetlen versenyző sem adott. Hét versenyző
teljesített 85% fölött, a tanulók 29%-ának a
teljesítménye viszont 40% alatt maradt.
A megoldásokból kiderült, hogy a feladat megoldásához
szükséges ismeretekkel (az elektromágnes
erőssége kapcsolatban van a tekercs menetszámával
és a tekercs meneteiben folyó áramerősséggel) a tanulók
többsége tisztában volt, de az arányosságot
nem fogalmazták meg, márpedig a kísérlet menetéből
erre is következtetni lehetett volna.
Kísérleti (mérő) feladat
- ) Határozd meg a jég olvadáshőjét a rendelkezésedre
álló eszközök, anyagok segítségével!
- ) A jég olvadáshője: L0 = 334 kJ/kg. Mi lehet az
oka annak, ha az általad kapott érték ettől eltér? Részletes
indoklást adj!
Eszközök, anyagok:
- 150 ml-es műanyag mérőhenger;
- 0 °C-os jégkockák;
- 0,5 literes pohár vízzel;
- vízhőmérő.
A víz fajhője: cvíz = 4200 kJ/kg °C
Gondold át alaposan a teendőket, s amikor felkészültél
a kísérleti feladat elvégzésére, a felügyelő tanároktól
kérj olvadó jégkockákat! A rendelkezésedre
álló időn belül többször is elvégezheted a mérést.
Értékelés
A 15 pontos kísérleti feladat átlag pontszáma 9,6
lett, ez 64%-os teljesítményt jelent. A feladat összeállítói
tisztában voltak azzal, hogy a jég olvadáshőjének
tanulókísérleti eszközökkel való mérése sok hibalehetőséget
tartalmaz, a táblázatbeli értéktől nagy eltérést
fog eredményezni. A mérési eljárás egyszerű, így a
legtöbb versenyző megszerezte a lehetséges pontszám
több mint felét a feladat megoldásában. A legtöbb
tanuló teljesítménye 47-80% közé esett.
Fizikatörténeti feladat 1
Keresztrejtvény volt Eötvös Loránd életéből és munkásságából.
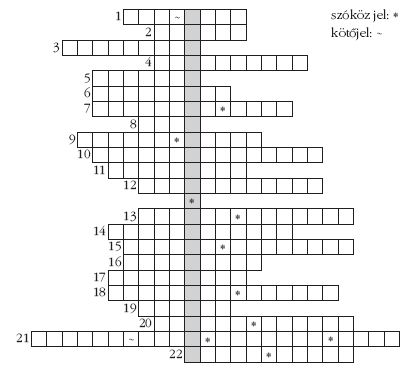
A keresztrejtvény függőleges fősorában Eötvös
Loránd egyik találmányának neve található, amely a
vízszintes sorok beírásával fejthető meg (két szó).
A sorok meghatározásai: 1. Hely, ahol az első gravitációs
terepi méréseket végezte. 2. Folyékony ásványkincs,
amelyet találmánya segítségével kutatnak fel. 3.
Az oktatásügyben betöltött magas tisztsége. 4. Külföldi
egyetemi tanulmányainak városa. 5. Ásványkincs, aminek
felkutatásában fontos szerepe van Eötvös Loránd
találmányának. 6. Egyik világhírű, egyetemi fizikatanára,
a spektrális analízis felfedezője. 7. Egyik találmánya,
amelyet télen alkalmazott. 8. A róla elnevezett fizikai
társulat mai rövidítése. 9. A dinamó feltalálója, akit Eötvös
Loránd a fizikai intézet igazgatói posztján követett.
10. Ebben a minőségben kezdte felsőfokú tanulmányait
még Magyarországon. 11. Itt neveztek el róla hegycsúcsot.
12. A francia kormány által adott kitüntetés. 13. A
kapilláris jelenséggel foglalkozó törvény neve. 14. Egyik
sportág, amit gyakran művelt. 15. Világhírű fizikus teljes
neve, akinek elméletét igazolta a súlyos és tehetetlen
tömeg arányosságának kimutatásával. 16. Személyéhez
fűződő tudományág. 17. Heidelbergi tanára, aki a fénytan
és a hangtan élettani részével ismertette meg. 18.
Magasrangú tudományos tisztsége. 19. Lovának neve.
20. Édesapja teljes neve. 21. Zseniális műszerének teljes
neve. 22. Édesanyja leánykori családi és utóneve.
Értékelés
Nemcsak a fősor, a vízszintes sorok megfejtései is
pontot értek. Minden vízszintes sor megfejtésére negyed
pont járt. Így a vízszintes sorok összesen 5,5
pontot értek, a fősorért 2,5 pont járt. A 8 pontot érő
megoldást mindössze két tanulótól kaptuk meg. A
versenyzők több mint fele 60-75% közötti teljesítményt
ért el. Öt tanuló eredménye volt 25%-os, vagy
kevesebb.



 Egy
cipőjavító műhelyben a cipész munkaasztalát
megvilágító lámpatestet két csigából álló szerkezettel
lehet lejjebb engedni, vagy
feljebb emelni. A rendszer
bármely helyzetben egyensúlyban
van. Minősítsd az
állításokat, ha a mozgócsiga
tömege elhanyagolható az
ellensúly tömegéhez képest!
Egy
cipőjavító műhelyben a cipész munkaasztalát
megvilágító lámpatestet két csigából álló szerkezettel
lehet lejjebb engedni, vagy
feljebb emelni. A rendszer
bármely helyzetben egyensúlyban
van. Minősítsd az
állításokat, ha a mozgócsiga
tömege elhanyagolható az
ellensúly tömegéhez képest!

 Egy
lombikot 10 °C hőmérsékletű
vízzel teletöltöttünk, majd lezártuk
egy olyan dugóval, amelynek a
közepét átfúrtuk. A furaton keresztüldugtunk
egy szorosan beleilleszkedő,
vékony üvegcsövet. Az
üvegcsőben a víz szintje - az ábrának
megfelelően - felemelkedett.
Mi történik a csőben levő víz szintjével,
ha a lombikot egy nagy kád jeges
vízbe tesszük, és megvárjuk, míg
a lombikban levő víz hőmérséklete
közel 0 °C-sá válik?
Egy
lombikot 10 °C hőmérsékletű
vízzel teletöltöttünk, majd lezártuk
egy olyan dugóval, amelynek a
közepét átfúrtuk. A furaton keresztüldugtunk
egy szorosan beleilleszkedő,
vékony üvegcsövet. Az
üvegcsőben a víz szintje - az ábrának
megfelelően - felemelkedett.
Mi történik a csőben levő víz szintjével,
ha a lombikot egy nagy kád jeges
vízbe tesszük, és megvárjuk, míg
a lombikban levő víz hőmérséklete
közel 0 °C-sá válik?




