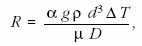Fizikai Szemle 2008/10. 359.o.
KONVEKCIÓ ÉGEN, FÖLDBEN, VÍZBEN
ÉS FOLYADÉKKRISTÁLYOKBAN
A konvekció - azaz a nem közvetlenül nyomásgradienssel,
hanem közvetett módon, más terekkel hajtott
anyagáramlás - jelen van mindenhol a minket körülvevő
világban. Leggyakoribb, közismert példája a
termikus térrel (hőmérséklet-gradienssel) gerjesztett
áramlás. A konvekció tipikusan nem-egyensúlyi folyamat,
beindulásához egymással versengő erők (vagy
forgatónyomatékok) egyensúlyának megbomlása
szükséges. Az erők egy része stabilizál. Amíg ezek
vannak túlsúlyban, addig a rendszer nyugalomban
van. Amikor a destabilizáló erők növekednek és az
előbbieket éppen kiegyenlítik, akkor indul be az instabilitás,
a folyamatot ezért egy küszöbtérrel lehet
jellemezni. A konvekció térben és/vagy időben inhomogén
anyageloszláshoz vezet, szabálytalan, periodikus
és turbulens örvényrendszereket, mintázatokat
hozva létre. A mintázatok igen változatos formákat
ölthetnek, tipikus a párhuzamos csíkrendszer és a
spirálszerkezet. Ezekre láthatunk példákat a hátsó
borító felvételein, ahol víztornádó, napfelszín, lávakőzet,
a Jupiter nagy vörös foltja, gleccser, viharfelhők,
lávató, hurrikán felülnézetben, elektrokonvekció folyadékkristályban,
tornádó a világűrben, a Perzsa-öböl
és egy gejzír látható.
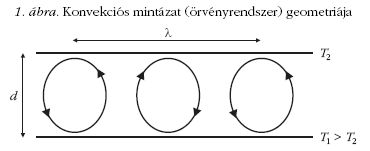
Termikus térrel, vagyis hőmérséklet-gradienssel vezérelt
konvekció ideálisan, laboratóriumi körülmények
között egy vízszintes, d vastagságú, alulról fűtött folyadékrétegben
valósulhat meg (1. ábra). Ez "konyhanyelven”
úgy hangzik, hogy végy egy serpenyőt, tölts
bele étolajat és tedd a tűzhelyre. A disszipatív hővezetés
és a viszkózus csillapítás a folyadékáramlást gátolja,
azaz stabilizál. A destabilizáció a hőtágulásból eredő
felhajtó erőnek, vagyis tulajdonképpen a gravitációs
térnek köszönhető: az alul lévő folyadékréteg melegebb,
tehát kisebb a sűrűsége, mint a felette levő hidegebb
rétegé. Ez tipikusan nem-egyensúlyi szituáció, az
egyensúly helyreállításához a rétegeknek helyet kell
cserélniük, ami csak úgy történhet, hogy az edény aljáról
kis, meleg folyadékcsomagok szabadulnak el a felszín
felé, amelyek helyére felülről hideg anyag áramlik.
Az eredmény konvekciós hengerek, örvények kialakulása
lesz, amelyekben az anyag a felszín és az aljzat
között zárt hurkok mentén áramlik (1. ábra). Az így
kialakult örvényrendszereket és magát a jelenséget
Rayleigh-Bénard-instabilitásnak hívjuk [1].
A jelenség értelmezéséhez az anyagsűrűség és az
áramlási sebesség térbeli és időbeli változásait kell
leírni. Ehhez a folyadékdinamika egyenleteiből (pl.
Navier-Stokes-egyenlet) kell kiindulni. Mivel csatolt,
parciális differenciálegyenletekről van szó, analitikus
megoldás csak bizonyos paramétertartományokban,
például a konvekció beindulási küszöbének közvetlen
környezetében, adható meg. Nagy meghajtó terek,
azaz nagy hőmérséklet-gradiens esetén az egyenletek
számítógépes szimulációja segíthet a megoldás keresésében.
A küszöb a határoló felületek közötti hőmérséklet-
különbség (ΔT = T1−T2)
növelésével érhető el,
de értéke függ a rendszerparaméterektől, azaz a hővezetés
(α), a hődiffúzió (D), a viszkozitás (µ), a sűrűség
(ρ) és a rétegvastagság (d) értékétől, valamint a
nehézségi gyorsulástól (g). E paraméterek dimenziótlan
kombinációja a Rayleigh-szám (R),
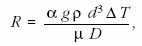
ami a vizsgált rendszer konvekcióra való hajlandóságát
fejezi ki, és a konvekció beindulásához - rendszerfüggetlenül
- körülbelül 1700-as értékét kell elérnie.
A Rayleigh-Bénard-instabilitást régóta és sokan
vizsgálták, ennek számos bizonyítékát találjuk az irodalomban
[1]. Az elért eredményeket felhasználhatjuk
számos, a természetben megfigyelhető jelenség értelmezésénél.
Termikusan hajtott konvekció bármilyen halmazállapotú
anyagban kialakulhat. Gázokban (pl. levegőben)
az áramlás nyomait mutatják a fűtőtest mögötti falon
lerakódott porcsíkok. De konvekció eredményei a
sztratoszférában kialakult struktúrák, felhőrendszerek,
időjárási frontok és azok dinamikája is, hiszen a Földet
körülvevő levegőréteg is erős hőmérséklet-gradiensnek
és gravitációs térnek van kitéve. A különböző trópusi
viharok (tájfun, hurrikán) és légtölcsérek (tornádó)
mind a konvekció látványos, bár sokszor katasztrófákat
előidéző példájául szolgálnak. Ha már az égen kalandozunk,
egy asztrofizikai példát is megemlíthetünk, a
csillagok belső anyagának turbulens keveredését.
A folyadékok konvektív instabilitásaira már említettük
a serpenyőben melegedő olaj példáját, ahol a
kellően felforrósodott alsó rétegből felfelé áramló
"buggyanatok” rendszere jól megfigyelhető a felszínen.
De nagyobb méretskálák felé is elmehetünk: a
tengeri és óceáni áramlatok is konvekció következményei.
A hatalmas tömegű víz körülbelül 10%-a vesz
részt a jól ismert felszíni áramlatokban (pl. a Golf-áramlat
Európa nyugati partjánál), de cirkulál a mélyben
a maradék 90% is, a kevésbé tanulmányozott
mélytengeri áramlatokban. Ez a rendszer természetesen
sokkal bonyolultabb a laboratóriumi kísérletnél,
ugyanis a tengerek nem csak alulról (a Földbelsejéből),
hanem felülről, a Naptól is melegszenek. Ezen
kívül, a rendszer forog, tehát a Coriolis-erőt is figyelembe
kell venni. Ráadásul a tengerfenék domborzata
változatos, azaz a vízréteg vastagsága nem állandó,
továbbá a tengerek sókoncentrációja is inhomogén és
a mélység függvénye. Konvekció zajlik a Földolvadt
magjában is. Ennek kiemelkedő jelentőségét az adja,
hogy a konvekcióhoz kapcsolódó dinamóeffektusnak
tulajdonítható a Föld mágneses tere, amely a földi élet
számára nélkülözhetetlen védelmet biztosítja a kozmikus
sugárzás ellen.
Hőmérséklet-gradiens hatására a szilárd anyag,
például a földkéreg - bármennyire hihetetlennek
tűnik - is áramlik. Bizonyított, hogy ugyanazok az
erők, amelyek a konvekciót vezérlik az atmoszférában
és az óceánokban, a szilárdföld kéregben is hatnak.
A Földbelsejének hője a felső rétegek konvekcióját
is vezérli, ami lassú, évente pár cm elmozdulást
okoz és plaszticitásnak nevezik. Ennek leírása még az
óceáni áramlatoknál is bonyolultabb eset, mert a változó
rétegvastagságon és a Coriolis-erőn kívül figyelembe
kell(ene) venni az anyag nagyfokú heterogenitását:
vannak lágy, laza részek, mint a termőföld és a
homok, illetve kemények, mint a sziklák és a különböző
összetételű és tulajdonságú kövületek, láva stb.
Az bizonyos, hogy a földkéreg lemezeinek folyamatos
egymásra csúszása, a tektonikus mozgás, földrengésekhez
vezet(het), amit kívánatos lenne minél pontosabban
leírni/megérteni, mert akkor az előrejelzés
lehetőségéhez is közelebb kerülhetnénk.
Bár eddig csupán termikusan gerjesztett konvekcióról
esett szó, a hőmérséklet-gradiens nem kizárólagos
beindítója az anyag örvényszerű áramlásának.
Egy egészen egzotikus példaként élő szervezetek
(bizonyos baktériumok) hada kollektív, cirkuláris
mozgást végez koncentrációgradiens (kemotaxis)
hatására. Kevésbé egzotikus, de igen érdekes példa
az elektromos térrel gerjesztett konvekció, ez azonban
izotróp közegben csak ritkán figyelhető meg. A
jelenség beindulását a releváns anyagi paraméterek
(dielektromos permittivitás, elektromos vezetőképesség)
anizotrópiája nagymértékben elősegíti. Ez a tulajdonság
elsősorban a kristályos anyagok sajátsága, de
bennük nehezen (vagy egyáltalán nem) hozható létre
áramlás. Az anizotróp folyadékok, azaz a folyadékkristályok
viszont ideálisak erre a célra [2].

A továbbiakban elektrokonvekcióról, vagyis folyadékkristályokban
elektromos térrel gerjesztett áramlási
örvényrendszerekről lesz szó. A jelenség alapgeometriáját
a termikus konvekcióhoz hasonlóan az 1.
ábra szemlélteti, csak ezúttal a vizsgált d vastagságú
anyagrétegre elektromos feszültséget (U = U1−U2)
kapcsolunk. A hőmérséklet-különbség szerepét az
elektromos potenciálkülönbség veszi át, vagyis az
instabilitást az elektromos tér hozza létre. Ebben a
kísérletben a rétegnek nem kell vízszintesnek lennie,
a jelenség szempontjából a gravitációnak nincs szerepe.
A stabilizáló tényezők itt a rugalmas és elektromos
forgatónyomatékok, valamint a viszkózus csillapítás,
a destabilizáló hatást pedig a tértöltések szétválásából
adódó erő képviseli, ami anyagáramlást indít
be, valamint az ezen áramlásból származó viszkózus
forgatónyomaték, ami átorientálódást eredményez [3,
4]. A kialakuló örvényrendszerek nagyon szabályosak,
a kontrollparaméterek - a meghajtó feszültség és
annak frekvenciája - a hőmérséklet-gradienssel ellentétben
könnyen szabályozhatóak. A kialakuló struktúráknak
az anizotrópia következtében nagy a kontrasztja,
így könnyen láthatóvá tehetők. Számos egyéb
praktikus előny (kis méret, olcsóság stb.) is hozzájárult
ahhoz, hogy a folyadékkristályokban zajló elektrokonvekció
széles körben elterjedt modellrendszerré
vált az anizotróp, sőt az izotróp konvekció tanulmányozására
is. Mivel az anyagi és kontrollparaméterek
széles skálája áll rendelkezésre, igen sokféle, lebilincselően
mutatós mintázat állítható elő. A 2. ábrán
néhány példa (kísérleti felvétel) látható.
Ezen struktúrák elméleti leírása is rendelkezésre
áll, vagy éppen kidolgozás alatt van. Itt is az áramló
folyadék mozgásegyenletéből kell kiindulni, de e
mellett figyelembe kell venni az átorientálást vezérlő
forgatónyomatékok egyensúlyát, a folyadék összenyomhatatlanságát
és az elektrodinamika egyenleteit
(mindezeket anizotróp anyagi paraméterekkel felírva).
Az eredmény egy 6 csatolt parciális differenciálegyenletből
álló rendszer, a hozzátartozó kezdeti és
határfeltételekkel, amelynek általában nincs analitikus
megoldása. Bizonyos fontos esetekben, például a küszöb
körül és közvetlenül felette, alkalmas közelítésekkel
(lineáris vagy enyhén nemlineáris stabilitásanalízis)
jól kezelhető és a kísérletekkel összevethető
eredmény kapható. Egyéb, analitikusan nem kezelhető
paraméter-tartományokban a számítógépes szimuláció
szolgál nagyon hasznos eszközként. Ideális esetben
a három módszer (kísérlet/mérés, egyenletmegoldás
és szimuláció) szimultán alkalmazása vezet a jelenség
egyre tökéletesebb megértéséhez.
A folyadékkristályok elektrokonvekciójának tanulmányozása
két szempontból is nagy gyakorlati jelentőségű.
Egyfelől a küszöböt lényegesen meghaladó feszültség
hatására a rendezett mintázatot felváltó turbulens
áramlás erős fényszórással jár, ami az eredetileg
átlátszó folyadékkristály-réteget átláthatatlanná teszi. Ez
az elektrooptikai effektus képezte a működési elvét az
első, az 1960-as évek végén megjelent folyadékkristálykijelzőknek,
és ez indította be azt a kiterjedt kutatásfejlesztést,
ami mára hatalmas gazdasági potenciált és
tömegtermelést képviselő iparág kifejlődéséhez vezetett.
Ez az iparág elégíti ki az órák, mobiltelefonok,
laptopok, lapos monitorok és televíziók folyadékkristály-
megjelenítői iránt gyorsan növekvő igényeket,
igaz, ma már más kijelzési elvet használva [5]. Másfelől
a kutatások megmutatták, hogy a különböző rendszerekben
zajló konvekciónak vannak rendszerfüggetlen,
általános törvényszerűségei. A folyadékkristályok elektrokonvekciója
terén elért egyes eredmények így más
konvekciós jelenségek részleteinek megértésében is
felhasználhatók. Ennek szükségessége és fontossága a
korábban bemutatott példák alapján nyilvánvaló, hiszen
időjárási katasztrófák, földrengések stb. megbízhatóbb
előrejelzéséhez vezethet.
Buka Ágnes, Éber Nándor
MTA SZFKI, Budapest
Irodalom
- I. Mutabazi, J.E. Wesfreid, E. Guyon (Eds.): Dynamics of Spatio-
Temporal Cellular Structures - Henri Benard Centenary
Review. Springer Tracts in Modern Physics, V. 207, Springer,
New York, 2006.
- P.G. de Gennes, J. Prost: The Physics of Liquid Crystals. 2nd
Edition, Clarendon Press, Oxford, 1993.
- Buka Ágnes, Tóth Katona Tibor, Börzsönyi Tamás, Tóth Péter:
Mintázatképző instabilitások folyadékkristályokban I. Fizikai
Szemle, 46 (1996) 376.
- Buka Ágnes, Tóth Katona Tibor, Börzsönyi Tamás, Tóth Péter:
Mintázatképző instabilitások folyadékkristályokban II. Fizikai
Szemle 47 (1997) 42.
- Éber Nándor: Folyadékkristály televíziók - a XXI. század képernyői.
Fizikai Szemle 56 (2006) 119.