MITŐL PEZSEG A PEZSGŐ? - Hogyan mozognak a buborékok a pezsgőben?

Nagy Anett
Radnóti Miklós Gimnázium, Szeged

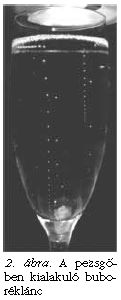
A fizika a körülöttünk levő világról szól, így még a legegyszerűbbnek tűnő jelenség alaposabb megvizsgálásához is nélkülözhetetlen. A pezsgős pohárban látható gyönyörű buborékláncok kialakulását és a buborékok mozgását is a fizika törvényeivel érthetjük csak meg. A következőkben megmutatjuk, hogy egy egyszerű fényképezőgép, egy számítógép, egy jó (!) pezsgőspohár és néhány üveg pezsgősegítségével hogyan mélyedhetünk el a buborékok mozgásának rejtelmeiben.

A táncoló mazsola, avagy a pezsgő ördöge

A hétköznapi eszközökkel végzett kísérletek nemcsak az iskolában használhatók fel a diákok tanítására, hanem az iskolán kívül is segíthetnek a fizika népszerűsítésében. Ezt már sokan és régen felismerték, amire jó példa lehet a következőkísérlet, amely egy 1903-ban kiadott könyvből származik. A kor hangulatát és beszédstílusát felelevenítve eredeti szövegezéssel is bemutatható és magyarázható a kísérlet. A kísérletet a leírás szerint "vidám lakoma végén kell elvégezni és magyarázatát a csodálkozó közönségnek azonnal meg kell adni". (1. ábra) [1].

"Vidám lakoma végén, mikor a pezsgős palackok szaporán ürülnek és szítják a jókedvet, ajánlkozzál, hogy fölidézed a társaság megrettentésére magát a Sátánt, mégpedig anélkül, hogy a középkorban dívott hókuszpókuszhoz folyamodnál. A csemegés tálból keress ki egy nagyobb szem jó száraz malaga-szőlőt, töltsd egy poharat tele pezsgővel és ejtsd bele a malaga- szőlő szemet. Csakhamar megindul a produkció. A pezsgőborból kifejlődő szénsav apró buborékokban lepi el a szőlőszemet s olyan hatással van rá, mintha valamely tárgyat léggömbök emelnének föl. Néhány másodperc alatt a szénsav-buborékok fölemelik a szőlőszemet a pohár felszínére. A szőlőszemről azonban, mihelyt a pohár felszínére ér, elillannak a szénsav- buborékok, a szőlőszem visszanyeri súlyát és lemerül a pohár fenekére. A pohár mélyén a szénsavbuborékok aztán újra megkönnyítik a szőlőszemet, az újra felemelkedik, aztán megint lemerül s ez a hintázás eltart vagy tíz percig, amíg tudniillik a pohárban levő pezsgőből a szénsav mind el nem szállt."

A CO₂ buborékok mérete és mozgása

Ez a látszólag egyszerű jelenség számos kérdést vet fel. Mitől "pezseg" a pezsgő? Mitől alakulnak ki a buborékok a pezsgőben és miért alkotnak hosszú láncot miközben a felszínre jönnek? Milyen törvények írják le a buborékok mozgását?

Az első kérdésre az a válasz, hogy a pezsgőoldott szén-dioxidot tartalmaz, méghozzá magasabb koncentrációban, mint a folyadék feletti levegő. A gyártás során a 200-500 kPa nyomáson megtöltik szén-dioxiddal az üveget, majd beletöltik a folyadékot (pezsgő, ásványvíz, üdítő). A gázok oldódási képessége növekszik a felette levőgáz nyomásának növelésével. A zárt, feltöltött üvegben a folyadék felszíne felett dinamikus egyensúlyi állapot alakul ki a folyadékban oldott és a gáz állapotú CO₂ között. Minél hidegebb az üdítő vagy a sör, annál nagyobb az oldott állapotú CO₂ mennyisége. Amint felnyitjuk az üdítős üveget, az egyensúly felborul és az oldott állapotú gáz buborékok formájában fokozatosan elhagyja a folyadékot.

Érdemes megvizsgálni, hogy arányában átlagosan mennyi szén-dioxid szabadul fel a szénsavas üdítőkből. Az üvegek címkéjén található adatok szerint a legtöbb üdítőital legalább 4,9 g CO₂-t tartalmaz literenként. A periódusos rendszer szerint a CO₂ moláris tömege 44 g. Egy mol gáz térfogata normál légköri nyomáson és szobahőmérsékleten 25 dm³. Ezek alapján az ideális gáztörvény segítségével megbecsülhető egy 0,5 literes üdítőben található oldott CO₂ térfogata:

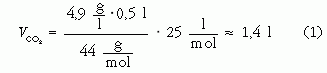
Vagyis a kapott térfogat majdnem háromszor akkora, mint az üdítőital térfogata! A meglepő eredményt értelmezve a diákok egy része felvetheti, hogy az oldott gáz egy része nem tudja elhagyni a folyadékot, hiszen a körülöttünk levő normál légköri nyomás 100 kPa. Vegyük figyelembe tehát azt, hogy az üdítős üvegekben túlnyomás uralkodik, átlagos esetben ez a normál légköri nyomás kétszerese. Ezek alapján a 0,5 literes üdítős üvegből felszabadult CO₂ térfogata 0,7 dm³. Tehát a szénsavas üdítőitalban oldott gáz térfogata nagyobb mint a folyadék térfogata [2].

A második kérdés megválaszolásához figyeljük meg a buborékképződés mechanizmusát. A folyadék belsejében a gáz apró buborékokban gyűlik össze, amelyek elérve egy bizonyos kritikus méretet feljönnek a felszínre. A buborékok azonban nem a folyadék belsejében keletkeznek, hanem a pohár belsőfelületén bizonyos pontokban. A felszín mikroszkopikusan kicsiny sérüléseiben megfelelőek a feltételek a buborékképződésekhez. A mazsola, földimogyoró vagy más tárgyak nem szabályos felszínük miatt szintén jó lehetőséget biztosítnak a buborékok kialakulására. A keletkező buborékok akkor szakadnak le a pohár felszínéről, amikor már elértek egy kritikus méretet. Ekkor a rájuk ható felhajtóerő meghaladja a buborék és az üveg között fellépő adhéziós kölcsönhatás nagyságát. Ez azonban nagyon rövid idő alatt bekövetkezik, mivel Ucke szerint [5] a felhajtóerő a buborék térfogatával, vagyis a sugár harmadik hatványával arányosan nő, míg az adhéziós erőlegfeljebb a buborék felületével, így a sugár négyzetével arányos. Ez azt jelenti, hogy az adhéziós erő a buborék sugarának növekedésével lassabban nő mint a felhajtóerő. Miután a buborék elhagyja keletkezési helyét, ott egy újabb keletkezik, ami szintén elérve a kritikus tömeget követi az előző buborékot egészen a felszínig. A buborékok mozgását alaposabban megfigyelve látható, hogy a buborékok mérete egyre növekszik miközben feljutnak a folyadék felszínére. A vizsgált folyadékban a pohár faláról levált buborékok mérete legalább a kétszeresére nő, amíg a felszínre jutnak. Ha ez a növekedés a hidrosztatikai nyomás csökkenésével lenne magyarázható, akkor a pohár alján a nyomásnak kétszer nagyobbnak kellene lennie a normál légköri nyomásnál. Ez azt jelentené, hogy a buboréknak legalább 10 m-t kellene emelkednie a folyadékban. Egy átlagos pohár magassága 15-20 cm. Tehát a buborékok méretének növekedése nem magyarázható a hidrosztatikai nyomás csökkenésével. A buborékok mérete azért növekszik a felszínre jutás során, mert nemcsak a keletkezéskor, hanem a mozgás során is CO₂ molekulák jutnak a buborékokba.

Érdemes néhány számítást elvégezni a széndioxidbuborékok mozgásával kapcsolatban. Amint az üdítős üveget kinyitjuk, az oldott szén-dioxid parciális nyomása a folyadékban nagyobb, mint a buborékokban levőszén-dioxid nyomása, ezért az oldott szén-dioxid a buborékba áramlik. Mivel ez a nyomáskülönbség megközelítőleg állandó a felnyitás után bizonyos ideig, feltételezhetjük, hogy a buborék méretének növekedése arányos a buborék felszínének változásával [3].

Ha feltételezzük, hogy a buborék megközelítőleg gömb alakú, és N a buborékon belüli a széndioxidmolekulák száma, γ pedig az arányossági tényező, akkor jó közelítéssel

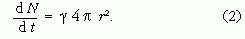
Ez az összefüggés azért írható fel ilyen egyszerű formában, mert az üdítőital állandó hőmérsékletet, a légkör pedig állandó nyomást biztosít. Tegyük fel azt is, hogy a pezsgőben, vagy az üdítőben található szénsav eleget tesz az ideális gázok állapotegyenletének, ahol tehát a nyomás és a hőmérséklet állandónak tekinthető a megfigyelés idejére:

p V = N k T,      (3)

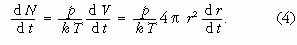
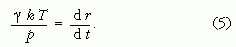
A differenciálegyenlet megoldása: r = r₀ + ut, ahol r₀ a kezdeti sugár és u = γkT/p, a buborék sugarának növekedési sebessége. A buborékok növekedésével kapcsolatos elméleti modell helyességének igazolására érdemes kísérleti eljárást kidolgozni. Mivel a pezsgőben vagy a sörben a buborékok gyönyörű láncot alkotva (2. ábra) jutnak a felszínre, lehetőségünk van néhány egyszerű mérés elvégzésére [3].

Az előbbiek szerint a pohár felszínén, bizonyos pontokban keletkeznek a buborékok, majd egy kritikus méretet elérve elhagyják keletkezési helyüket. Amint elváltak a pohár felszínétől, az adott pontban újabb buborék keletkezik. Mivel minden buborék ugyanazon a folyamaton megy keresztül, feltételezhetjük, hogy megközelítőleg egyenlő idők telnek el a buborékoknak a pohár felszínéről való leválása között. Így ha megszámoljuk, hogy a buborékláncban adott idő alatt hány buborék jut el a felszínre, következtethetünk a buborékok felszínről való leválásának sebességére. A kísérletet sörrel elvégezve azt tapasztaltuk, hogy átlagosan 112 buborék ért az adott láncból a folyadék felszínére 1 perc alatt. Ez azt jelenti, hogy 0,53 másodpercenként hagyja el egy-egy buborék a pohár felszínének adott pontját. A kísérletet száraz pezsgővel végezve 20 s alatt átlagosan 70 buborékot számoltunk meg, amely azt jelenti, hogy egy buborék keletkezéséhez és elszakadásához átlagosan 0,28 másodpercre van szükség.

1. táblázat A buborékok mozgását jellemző mennyiségek
a buborék korrigált átmérője (mm)	a buborékok keletkezése közötti idő(s)	távolság a buborékok között (mm)	a buborék által megtett út (mm)
0,220	0,00	0,00	0,00
0,230	0,14	0,52	0,52
0,240	0,28	0,66	1,18
0,250	0,42	0,79	1,97
0,26	50,56	0,87	2,84
0,280	0,70	1,05	3,89
0,290	0,84	1,15	5,04
0,305	0,98	1,36	6,40
0,310	1,12	1,40	7,80
0,320	1,26	1,70	9,50
0,330	1,40	1,81	11,31
0,340	1,54	2,01	13,32
0,350	1,68	2,49	15,81
0,360	1,82	2,48	18,29
0,376	1,96	2,79	21,08
0,390	2,10	2,93	24,01
0,400	2,24	3,20	27,21
0,411	2,38	3,92	31,13
0,425	2,52	4,02	35,15
0,440	2,66	4,31	39,46
0,460	2,80	4,52	43,98
0,470	2,94	4,47	48,45
0,490	3,08	4,63	53,08
0,520	3,22	4,40	57,48

A buborékok méretének vizsgálatakor nem szabad figyelmen kívül hagynunk, hogy mind a folyadék, mind a pohár fala megváltoztatja a buborék látszólagos méretét. A buborékok nagyobbnak látszanak, mint amilyenek valójában. A buborékok tényleges sugarát és a közöttük levőtávolságot például egy ismert átmérőjű, azonos távolságokban megjelölt drót segítségével mérhetjük meg. Helyezzük a drótot a folyadékba a buboréklánc mellé. Fényképezzük le a buborékokat a dróttal együtt. A képet kinagyítva a drót valódi átmérőjének és a beosztások közötti távolságnak az ismeretében meghatározható a buborék sugarának változása a felszínre jutás során. Kísérletünkben a függőleges mozgás miatti esetleges torzulás elkerülése végett a buborékok horizontális átmérőjét hasonlítottuk össze a drót vastagságával, amiből meghatároztuk a nagyítás mértékét a pohár aljától való távolság függvényében.

Meg kell jegyeznünk azonban, hogy a fényképek felbontóképességének határa miatt a buborékok átmérőjének leolvasása kis bizonytalanságot rejt magában. A minél pontosabb eredmények érdekében a nagyon kis expozíciós idővel (1/800 s) készített a fényképeket az AUTOCAD program segítségével elemeztük ki, amellyel a buborékok átmérőjét a fénykép igen nagy nagyíthatóságának köszönhetően viszonylag pontosan le tudtuk olvasni (±0,01 mm). A pontosabb mérés érdekében a kísérletet megismételtük egy kis méretű, párhuzamos falú üvegkáddal is, amely esetben a nagyítás miatti korrekció értéke a párhuzamos falak következtében állandó. A mérési eredményeket az 1. táblázat tartalmazza.

Vizsgáljuk meg, hogy a buborék átmérője hogyan változik az idő függvényében. Feltételezhetjük, hogy a buborék mérete az eltelt idővel arányosan nő a diffúzió miatt. A buborékok átmérőjét az idő függvényében ábrázolva lineáris függvényt kapunk (3. ábra), amelynek meredeksége a buborék növekedési sebességét adja számértékben, míg tengelymetszete a buborék kezdeti méretét a leválás pillanatában.

A buborék kezdeti átmérőjére 0,2133 mm-t kapunk, míg a növekedés sebességére 0,0868 mm/s adódott.

Mivel a buborék mérete növekszik, a felemelkedési sebessége is egyre nagyobb lesz. Ez a fényképeken is jól látszik, mert a buborékok közötti távolság a pohár aljától távolodva nő. Feltételezhetjük, hogy a buborék keletkezése és elszakadása a felszíntől egyenlő időközönként történik. Tehát a buborékok által egységnyi idő alatt a keletkezési ponttól megtett utakat ábrázolva az időfüggvényében egy gyorsuló mozgás grafikonját kaphatjuk (2. táblázat, 4. ábra).

A grafikonra egy másodfokú függvényt illesztettünk, amelyről a gyorsulás értéke meghatározható. Mivel az egyenletesen változó mozgás úttörvénye:

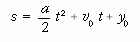
alakú, ezért a gyorsulás értéke a = 11,218 mm/s².

A buborékok gyors mozgása miatt a hosszabb expozíciós idejű felvételeken a buborék éles körvonala helyett egy kis csík látható, amelynek hossza arányos a buborék pillanatnyi sebességével (5. ábra). Ezek a felvételek ezért alkalmasak arra, hogy másik módszerrel is meghatározzuk a buborékok gyorsulását. Ha az expozíció ideje 1/15 s, akkor ez azt jelenti, hogy a buborék 1/15 s alatt az adott csíknak megfelelő, azzal azonos hosszúságú utat tett meg. Így a vonalak hosszának ismeretében a buborék sebessége számolható. A mérési eredményeket a 2. táblázat tartalmazza.

2. táblázat A buborékok nyomképének hossza és az emelkedés sebessége 1/15 s záridő esetén
a buborékok keletkezése közötti idő(s)	a nyomképvonal hossza (mm)	emelkedési sebesség (mm/s)
0,00	0,34	5,10
0,14	0,40	6,00
0,28	0,43	6,45
0,42	0,49	7,35
0,56	0,54	8,10
0,70	0,66	9,90
0,84	0,75	11,25
0,98	0,87	13,05
1,12	0,94	14,10
1,26	1,04	15,60
1,40	1,14	17,10
1,54	1,33	19,95
1,68	1,44	21,60
1,82	1,50	22,50
1,96	1,59	23,85
2,10	1,71	25,65
2,24	1,88	28,20
2,38	2,01	30,15
2,52	2,12	31,80
2,66	2,25	33,75
2,80	2,34	35,10
2,94	2,45	36,75
3,08	2,55	38,25
3,22	2,79	41,85

Ha a buborékok sebességét az időfüggvényében ábrázoljuk (6. ábra), akkor egy lineáris függvényt kapunk, melynek meredeksége a buborék gyorsulása. A kísérletben a gyorsulás értékére 11,564 mm/s²-t kaptunk, ami jól egyezik a másik eljárással meghatározott gyorsulás értékével.

A buborék mérete és felemelkedési sebessége közötti kvantitatív összefüggés nagyon bonyolultan adható meg. Egy adott méretű buborék esetén azonban könnyen megbecsülhető. Most vizsgáljuk meg, hogy mi miatt és hogyan emelkednek a buborékok a folyadékban. Mivel a CO₂ sűrűsége kisebb, mint az őt körülvevő folyadék sűrűsége, ezért a buborék a pohárban felfelé mozdul el. Mozgását a felhajtóerő, a gravitációs erő és a közegellenállási erő együttesen határozza meg.

A felhajtóerő Arkhimédész törvénye szerint arányos a gömb alakú buborék által kiszorított folyadék térfogatával. Tételezzük fel, hogy a gáz sűrűsége jóval kisebb mint a folyadék sűrűsége:

F ≈ V ρ_f g,      (6)

pedig a gravitációs gyorsulás. Tételezzük fel azt is, hogy a buborék olyan kicsi és annyira lassan halad, hogy mozgása során mindvégig megőrzi gömb alakját. Ekkor a felhajtóerő a buborék sugarának köbével arányos:

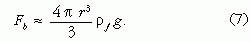
A buborékot mozgása során a közegellenállási erő lassítja. Általánosságban az emelkedőbuborékra ható közegellenállási erő a sugár, az emelkedési sebesség, a viszkozitás, a sűrűség és a folyadék felületi feszültségének összetett függvénye [4].

Ha feltesszük, hogy az emelkedőbuborék adott méretű, akkor egy bizonyos idő után sebessége elér egy állandó értéket, amikor is a felhajtóerő kiegyenlíti a közegellenállási erőt. Azonban a diffúzió miatt a buborék sugara folyamatosan nő, a felhajtóerő a sugár köbével arányosan nő, amivel a közegellenállási erő nem tud egyensúlyt tartani, hiszen az a sugár négyzetével, azaz kevésbé növekszik. Tehát a felfelé mutató felhajtóerő gyorsabban nő, mint a lefelé mutató közegellenállási erő, a buborék ezért gyorsuló mozgást végez. Ez magyarázza azt, hogy a buborékláncban a buborékok a pohár alján kisebbek és közelebb vannak egymáshoz, mint a felszín közelében.

A buborék mozgásának jellemzéséhez írjuk fel a dinamika alapegyenletét:

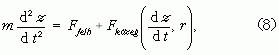
ahol m a buboréknak és annak a folyadéknak az együttes tömege, melyet a buborék mozgása során magával visz, dz/dt a buborék emelkedési sebessége. Ha feltesszük, hogy a buborékra ható gravitációs erő jóval kisebb, mint a közegellenállási és a felhajtóerő, az egyenlet a következőalakot veszi fel:

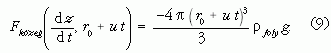
Az egyenlet megoldása független a buborék kezdeti sebességétől. A közegellenállási erő meghatározása igen összetett feladat viszkózus közegben mozgó buborék esetére, ezért empirikusan meghatározott korrelációk segítségével jósolhatjuk meg a mozgást.

Ha a Stokes-törvény segítségével írjuk fel a közegellenállási erőt, akkor

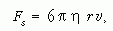
ahol például η(20 °C) = 0,001 Pa · s a víz (a folyadék) viszkozitása, r = 0,1 mm egy átlagos buborékméret röviddel az elszakadás után, v pedig a felfelé mozgás sebessége [5, 6]. Ezen összefüggések felhasználásával a következőeredményt kapjuk, ami összhangban van a megfigyelés tapasztalataival:

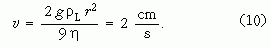
Az összefüggés alapján tehát az várható, hogy a buborék emelkedési sebessége a sugár négyzetével arányosan változik. Ha tehát a sebességet a sugár második hatványának függvényében ábrázoljuk, akkor jó közelítéssel lineáris grafikont (7. ábra) kell kapnunk [7].

Az egyenes meredeksége 835,18 mm^-1 s^-1, ami - a megfelelőadatok behelyettesítése után - durva közelítésben megegyezik az előbbi levezetésben kapott együttható értékével.

Irodalom

1. Good A.: Tom Tit második száz legújabb kísérlete. Atheneum, Budapest, 1893.
2. Planinsic G.: Fizziology. Physics Education 39/1 (2004) 65-68.
3. Shafer N., Zare R.: Through a beer glass darkly. Physics Today (1991) October, 48-52.
4. Krishna R., Baten J. M.: Simulating the motion of gas bubbles in a liquid. Nature 398 (1999) March, 208.
5. Ucke Ch. Schlichting H. J.: Why does champagne bubble? Physics and Technology Quest 2/1 (1997) 105-108.
6. Litz J.: Hőtan. Dialóg Campus Kiadó, Pécs-Budapest, (2001) 504.
7. Vermillion R. E.: A look at some rising bubbles. American Journal of Physics 43/2 (1975) 177-179.