XI. SZILÁRD LEÓ NUKLEÁRIS TANULMÁNYI VERSENY
Beszámoló, I. rész

Sükösd Csaba
BME Nukleáris Technika Tanszék

Szilárd Leó születésének centenáriuma alkalmából, Marx György professzor kezdeményezésére 1998-ban került először megrendezésre a Szilárd Leó Országos Középiskolai Tanulmányi Verseny. Azóta a Szilárd Leó Tehetséggondozó Alapítvány és az Eötvös Loránd Fizikai Társulat minden évben megrendezi a versenyt. 2006 óta határon túli magyar anyanyelvű iskolák tanulói részére is megnyitottuk a részvétel lehetőségét. Az idén ezzel három erdélyi iskola, a Báthory István Elméleti Líceum (Kolozsvár), a János Zsigmond Unitárius Kollégium (Kolozsvár), valamint a Nagykárolyi Elméleti Líceum (Nagykároly) élt, ahonnan összesen tizenkét első kategóriás (11-12. osztályos), és huszonkilenc junior kategóriás tanulót neveztek be a versenybe. Sajnos Felvidékről, Vajdaságból és Kárpátaljáról 2008-ban sem kaptunk nevezéseket. Összesen 215 első kategóriás és 113 junior kategóriás nevezés érkezett.

A 2008. február 25-én megtartott első forduló (válogató verseny) tíz feladatát az iskolákban lehetett megoldani három óra alatt. Kijavítás után a tanárok azokat a megoldásokat küldték be a BME Nukleáris Technika Tanszékére, ahol a 9-10. osztályos (junior) versenyzők legalább 40%-os, a 11-12. osztályos (I. kategóriás) versenyzők legalább 60%-os eredményt értek el. Ezeket ellenőrizve egy egyetemi oktatókból álló bírálóbizottság a legjobb 10 junior és a legjobb 20 első kategóriás versenyzőt hívta be a paksi Energetikai Szakközépiskolában 2008. április 19-én megrendezett döntőre. A döntőn minden behívott versenyző megjelent. Az idén négy lány is bejutott a döntőbe, mindannyian az I. kategóriában. A verseny fordulóin (mobiltelefon és internet kivételével) bármilyen segédeszköz használható volt.

Az alábbiakban ismertetjük a válogató verseny, valamint a döntő feladatait, és röviden a megoldásokat. Valamennyi feladatra 5 pontot lehetett kapni.

A válogató verseny (I. forduló) feladatai

1. Miért állíttatta le az USA Reaktorbiztonsági Bizottsága a grafit moderátoros, vízhűtésű reaktorokat már 1953-ban?
2. Melyik magyar származású tudós volt elnöke ennek a bizottságnak?

2. feladat

A következő idézet Marie Curie 1903-ban készült doktori értekezéséből való.

"Indukált radioaktivitás létesíthető úgy is, hogy egyes anyagokat urániummal együtt oldunk fel. A kísérlet báriummal sikerült. Ha Derierne eljárása szerint kénsavat töltünk urániumot és báriumot tartalmazó oldatba, a lecsapott báriumszulfát aktivitást visz magával, ezalatt az urániumsó aktivitásának egy részét elveszíti. Becquerel azt találta, hogy többször ismételve ezen eljárást, oly urániumot kapunk, mely már alig aktív. Azt lehetne hinni ezek után, hogy ezen eljárással sikerült az urániumtól egy ezen fémtől különböző radioaktív testet elválasztani, amelynek jelenléte okozza az uránium aktivitását. Ez azonban távolról sincs így, minthogy néhány hónap múlva az uránium visszanyeri eredeti aktivitását, a lecsapott bárium- szulfát ellenben elveszti nyert aktivitását. Hasonló jelenség megy végbe a tóriummal."

Mi lehet a magyarázata a fenti idézetnek?

Megoldás: A kémiai kezeléssel az urán bomlási sorának többi elemét távolították el. A maradék tiszta urán már alig mutat radioaktivitást. Pár hónap múlva ismét felszaporodnak a bomlástermékek, ezért nő meg a minta aktivitása. Az eltávolított bomlástermékek felezési ideje jóval kisebb, mint az uráné, ezért azok aktivitása gyorsan csökken.

3. feladat

Az α-bomlást gyakran kíséri negatív β-bomlás, de pozitív β-bomlás és elektronbefogás nem. Mi lehet ennek az oka?

Megoldás: Az α-bomlás a nehéz elemek tulajdonsága, és ezeknél az atommagoknál az energiavölgy már jócskán elhajlik a Z = N egyenestől a neutrontöbblet felé. A bomlás során a protonok és a neutronok száma ugyanannyival (kettővel) csökken, ezért a neutron/ proton arány növekszik. A neutrontöbblet relatív növekedése miatt a negatív béta-bomlás közelebb visz az egyensúlyi állapothoz, hiszen a neutronok száma csökken, a protonok száma pedig nő. Pozitív béta-bomláskor és elektronbefogáskor a neutronok száma nőne és a protonok száma csökkenne, ezért ez az egyensúlyi helyzettől még távolabb vinne.

4. feladat

Egy röntgencső másodpercenként 10¹⁵ darab, átlagosan 150 pm hullámhosszúságú fotont bocsát ki, ha 100 kV feszültségen 50 mA áramot vesz fel. Mekkora hatásfokkal működik a cső? Mire fordítódik a felvett energia jelentős része?

Megoldás: A felvett teljesítmény: P_fel = U · I = 100 kV · 50 mA = 5000 W, a leadott hasznos teljesítmény (az 1 s alatt kibocsátott fotonok által elvitt energia):

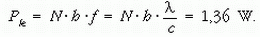
A hatásfok tehát:

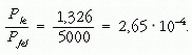
A felvett energia legnagyobb része az anód anyagát melegíti!

5. feladat

Torinóban őriznek egy leplet, amelyről sokan azt gondolják, hogy Krisztus halotti leple volt. A lepel korát 14C vizsgálattal kívánták meghatározni. A mérés szerint a lepel a XIV. század közepéből (kb. 1350-ből) származik. Hogy aránylik egymáshoz a minta 14C aktivitása és az, ami akkor lenne, ha a lepel valóban 2000 éves lenne?

Megoldás: Az aktivitás az időnek exponenciális függvénye. A(t) = A(0) · 2^-t/T, ahol T = 5568 év, a radiokarbon felezési ideje. Ebből: A(2000) = A(0) · 2^-2000/5568, illetve A(650) = A(0) · 2^-650/5568.

A két aktivitás aránya:

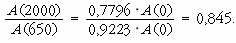
Tehát, ha 2000 éves lenne, akkor a jelenlegi aktivitás 0,845-szörösét kellene mutatnia.

A megoldás során feltételeztük, hogy a lepel kezdeti aktivitáskoncentrációja A(0) független attól, hogy mikor készült a lepel.

6. feladat

Határozd meg egy ciklotronból kilépő protonok maximális mozgási energiáját, ha tudjuk, hogy a ciklotron átmérője d, a gyorsítófeszültség frekvenciája pedig f.

Megoldás: A ciklotronban a protonok körpályán tartásához szükséges centripetális erőt a mágneses Lorentz-erő biztosítja. Az erők abszolút értékére vonatkozó egyenlet:

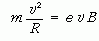
(mivel a sebesség és a mágneses mező merőlegesek egymásra). Ebből kapjuk:

A maximális mozgási energiához v_max kell, ami akkor következik be, amikor a protonok pályasugara a lehető legnagyobb: R = d/2. Így kapjuk:

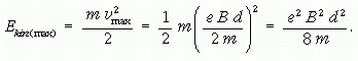
A gyorsítás feltétele, hogy az alkalmazott feszültség periódusideje (1/f ) egyezzen meg a protonok körülfordulási idejével, azaz

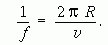
Ide (*)-ból behelyettesítve a sebességet kapjuk

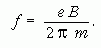
Ebből eB = 2π · f · m, amelyet a maximális energia kifejezésébe helyettesítve kapjuk:

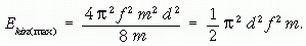
7. feladat

A technécium (Z = 43) egyik izotópja sem stabil, mesterségesen állítják elő. Az Észak-Amerika ⁹⁹Tc ellátásáért felelős kanadai kutatóreaktort (NRU, Chalk River, Ontario) 2007 novemberében biztonsági problémák miatt a tervezettnél hosszabb időre le kellett állítani. A földrész technécium-ellátása ezzel megbénult. Figyelembe véve a heti átlag 300 000 db ⁹⁹Tc alapú orvosi vizsgálatot, a kanadai kormány a biztonsági aggályok ellenére egy hónappal később újraindíttatta a reaktort.

A ⁹⁹Tc izotópnak van egy körülbelül 6 óra felezési idejű gerjesztett (metastabil) állapota ^99mTc, amelyből γ-sugárzás kibocsátásával bomlik el. Emiatt, és egyéb tulajdonságai miatt is, alkalmas szív- és érrendszeri diagnosztikai vizsgálatokra. (Teller Edénél is alkalmazták 1979-ben, amikor infarktusa volt.) Rövid felezési ideje miatt a helyszínen, a kórházban kell elválasztani egy "szülő" izotóptól, amelyből keletkezik, és amellyel radioaktív egyensúlyban van. Ezt a szülő izotópot állítják elő atomreaktorokban.

1. Mi lehet a "kezdő" stabil atommag (amit be kell tenni a reaktorba)?
2. Mi lehet a "szülő" atommag (amelynek a bomlásából a ^99mTc keletkezik)?
3. Általában milyen feltételeknek kell eleget tegyen egy diagnosztikára használt radioizotóp felezési ideje, illetve az őt szülő izotóp felezési ideje?

Megoldás:

1. ) A "kezdő"-mag a molibdén (Z = 42) 98-as tömegszámú stabil izotópja lehet, mert reaktorban neutronnal besugározva nem stabil 99-es izotópot kapnak az alábbiak szerint:

   

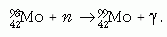
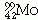2. ) A "szülő"-mag természetesen a radioaktív mag a következők szerint 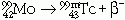(a Tc metastabil gerjesztett állapotban keletkezik, ezt jelzi az "m") 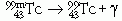(felezési idő kb 6 óra). A vizsgálatban ezt a γ-sugárzást detektálják. A Mo-Tc rendszerben körülbelül egy nap alatt beáll a radioaktív egyensúly. A keverékből a technéciumot kémiai módszerekkel a kórházban elválasztják, és így használják nyomjelzésre.
3. ) A vizsgálat szempontjából az a jó, ha a beadott radioaktív izotóp felezési ideje rövid, mert ekkor kis mennyiség is viszonylag nagy aktivitású, viszont hamar lebomlik, és nem terheli sokáig a beteg szervezetét. A szülő-izotóp esetében viszont nem szabad túl rövidnek lenni a felezési időnek, mivel ezt el kell szállítani a reaktortól a kórházba, és közben nem szabad nagyon lebomlania. Túl hosszú felezési idő sem jó, mert akkor a szükséges aktivitás eléréséhez nagy anyagmennyiségre lenne szükség. A ⁹⁹Mo felezési ideje 66 óra, ami egy ésszerű kompromisszum.

8. feladat

Hidrogénatom gerjesztett elektronja az n = 5 állapotból az n = 1 állapotba kerülve kibocsát egy fotont. Legfeljebb mekkora mozgási energiájú fotoelektront képes ez a foton kiváltani fém nátriumból? A nátrium kilépési munkája 2,75 eV.

Megoldás: A hidrogénatomban lévő elektron energiája alapállapotban: E₁ = -2,19 aJ. Az n = 5 gerjesztett állapotban az energia E_n = E₁/n², azaz E₅ = -2,19/25 aJ. Az energiakülönbség, és egyben a kilépő foton energiája: ΔE = E₅-E₁ = 2,1 aJ. A nátrium kilépési munkája: W_ki = 2,75 eV = 4,4 · 10^-19 J = 0,44 aJ. A maximális mozgási energia nyilván a két energia különbsége, azaz 1,66 aJ.

9. feladat

1. Becsüld meg, mekkora sugárdózist jelenthet egy 50 kg tömegű ember számára percenként a tőle 1 méterre álló, 20 MBq aktivitású jódizotóppal kezelt beteg, ha feltételezzük, hogy annak testét a 356 keV energiájú fotonok fele hagyja el, és az emberünket érőknek is a fele nyelődik el benne? (Vegyük úgy, hogy az ember a testének 1 m²-nyi felszínét fordítja a sugárforrás felé.)
2. Hány vízmolekula felbontásához lenne elegendő ez az energia? (Adatok a függvénytáblázatban.)

Megoldás: Az egy perc alatt keletkezett fotonok összes energiája 6,8 · 10^-5 J. Ennek csak fele lép ki, azaz a kilépő energia percenként 3,4 · 10^-5 J. A jód az ember pajzsmirigyében nyelődik el, ezért pontszerű sugárforrásnak tekinthető. Emiatt az összes kibocsátott foton F/(4πR²) = 1/(4π)-ed része esik az emberre (mivel F = 1 m² és R = 1 m). A testét elérő fotonoknak (és így az energiának is) csak a fele nyelődik el, tehát az elnyelt energia

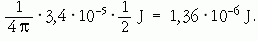
Az elnyelt dózis:

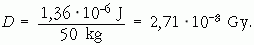
A víz kötési energiája 498 kJ/mol, tehát egy vízmolekula elbontásához

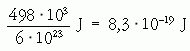
energia kell. Így az egész testben elnyelt energia

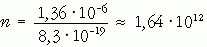
vízmolekulát tud elbontani.

10. feladat

A Genf melletti CERN-ben épül a világ legnagyobb részecskegyorsító berendezése, az LHC (Nagy Hadronütköztető). A föld alatti alagútban lévő gyorsító gyűrűnek 27 km a kerülete, és benne 7 TeV (= 7 · 10¹² eV) energiájú protonok keringenek majd. Mekkora mágneses indukciót kell létrehozni az eltérítő mágnesekben a protonok körpályán tartásához, ha az 1232 db eltérítő mágnes mindegyike 14,3 m hosszú?

Megoldás: A 27 km kerületű LHC-nek vannak egyenes szakaszai is, ezért nagyobb a kerülete, mint a mágnesek teljes hosszúsága! A "körpályán" tartás azonban csak az eltérítő mágnesekben történik. A mágnesek teljes hossza 1232 · 14,3 m = 17617,6 m. Ez azt jelenti, hogy ha a mágneseket egymás mellé helyeznénk, akkor egy ekkora kerületű kört kapnánk. Ennek a körnek a sugara: R = 2804 m lenne. A körpályán tartáshoz szükséges centripetális erőt a mágneses Lorentz-erő biztosítja:

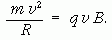
Ebből kapjuk:

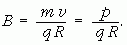
Itt p a részecske lendületét jelenti. A protonok nyugalmi tömegére mc² ~ 0,938 GeV ~ 0,001 TeV. Ezért a 7 TeV-es protonok erősen relativisztikus részecskék, így lendületükre nagyon jó közelítéssel: p = E/c. Ezt beírva kapjuk:

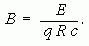
Az ismert mennyiségek behelyettesítésével egyszerűen adódik: B = 8,32 T. Ilyen nagy mágneses indukciót csak szupravezető mágnesekkel lehet előállítani.

Az elődöntő feladatait 51 fő I. kategóriás, és 16 fő junior versenyző teljesítette olyan szinten, hogy dolgozataikat a javító tanárok tovább tudták küldeni a BME Nukleáris Technika Tanszékére további rangsorolás végett. A beküldött dolgozatokból választotta ki a zsűri a legjobb húsz I. kategóriás, és a legjobb tíz junior versenyzőt, akiket behívtak a döntőbe.

A döntő versenyfeladatai

1. feladat (kitűzte: Radnóti Katalin)

Mikor, hol és kivel együtt kezdett el foglalkozni Teller Ede a magfúzióval? Milyen felismerésekre vezetett ez?

Megoldás: 1938-ban George Gamow-val dolgozta ki a magfúzió elméletét, ezzel magyarázták meg a csillagok energiatermelését. Ekkoriban Gamow és Teller a George Washington Egyetemen tanított. A Manhattanprojekt során Fermi tette fel neki a kérdést, hogy egy atombombával be lehetne-e indítani a magfúziót (1942). Ez az ötlet vezetett el a hidrogénbombához (első amerikai kísérleti robbantás 1952. november 1-jén volt).

2. feladat (kitűzte: Sükösd Csaba)

A napállandó értéke 1388 W/m². Ezt az adatot (valamint a Nap működésének ismeretét) felhasználva határozzuk meg, hogy másodpercenként hány, a Napból származó neutrínó szeli át testünk minden négyzetcentiméterét!

Megoldás: A Nap fúzióból nyeri az energiáját. Ennek során (több részfolyamat eredményeképpen) gyakorlatilag 4 protonból keletkezik egy darab ⁴He mag, "melléktermékként" pedig két neutrínó és 26,71 MeV = 4,2794 pJ energia. Feltesszük, hogy a neutrínók és az energia kibocsátása egyaránt izotróp, és hogy terjedésük az űrben egyformán 1/R²-es törvény szerint gyengül. Ekkor azt lehet mondani, hogy minden 2,1397 pJ-os energiacsomag mellé egy neutrínó is társul. Ez adja meg az összefüggést az energia és a neutrínószám között. Eszerint egy négyzetméterre másodpercenként N = 1388  / (2,1397 · 10^-12) = 6,486 · 10¹⁴ darab neutrínó jut, ami egy négyzetcentiméterre számolva 64,86 milliárd neutrínó másodpercenként.

Megjegyzés: A megoldás során feltételeztük, hogy a felszabaduló energia teljes egészében olyan formában sugárzódik ki, ami beleszámít a napállandó értékébe. Ez a valóságban nincs így, mert a kisugárzott neutrínók is visznek el több-kevesebb energiát (a részfolyamattól függ, hogy éppen mennyit).

3. feladat (kitűzte: Czifrus Szabolcs)

A közeli jövő egyik legnagyobb neutronfizikai kutatócentruma az ESS (Európai Spallációs Forrás) lesz, amely reményeink szerint Magyarországon fog megépülni. A berendezésben egy protonnyalábbal valamilyen nehézfémből készült céltárgyat bombáznak, amelyből a protonok neutronokat váltanak ki. A protonok energiája 1 GeV, a protonnyaláb árama 150 mA. A nyaláb impulzusszerűen működik, másodpercenként 16-szor 2 ms időtartamra. Tegyük fel, hogy az ehhez szükséges elektromos energia atomerőműből származik. Évente hány mol uránt kell elhasítani az erőműben az ESS nyalábjához szükséges elektromos energia biztosítására, ha az atomerőmű hatásfokát 33%-nak tekintjük? Hogyan aránylik az ezekben a hasadásokban másodpercenként keletkező neutronok száma az ESS-ben keletkező neutronok számához képest? (Az ESS-ben 1 proton becsapódása átlagosan 30 neutront vált ki.)

Megoldás: Az ESS-ben egy impulzus teljesítménye 1 GV · 150 mA = 0,15 GW. Egy másodperc alatt csak 16 · 2 ms = 32 ms-ig működik a nyaláb, tehát az átlagos teljesítmény P = 0,032 · 0,15 GW = 4,8 MW. Az átlagos áram 4,8 mA, amiből kapjuk, hogy a céltárgyba átlagosan becsapódó protonok száma 4,8 · 10^-3/(1,602 · 10^-19) ~ 3 · 10¹⁶ proton/s. Tehát a neutronok átlagos forráserőssége (azaz a másodpercenként kibocsátott neutronok száma) az ESS céltárgya mögött ennek körülbelül harmincszorosa, vagyis nagyjából 9 · 10¹⁷ neutron/s.

Számoljuk ki, hogy másodpercenként hány hasadás kell ehhez a teljesítményhez! Egy hasadásban 198 MeV energia szabadul fel, ami 3,17 · 10^-11 J. Nekünk másodpercenként 3 · 4,8 MJ hasadásból származó energiára van szükségünk (figyelemmel az atomerőmű hatásfokára), amihez másodpercenként 4,54 · 10¹⁷ hasadás kell. Az összes felszabaduló neutronszám ekkor átlagosan ennek 2,4 szerese, azaz 1,09 · 10¹⁸ neutron másodpercenként. Látható, hogy ez a szám alig 20%-kal nagyobb, mint az ESS-ben egy másodperc alatt felszabaduló neutronszám. Mivel a láncreakció fenntartásához hasadásonként egy neutronra szükség van, és a neutronok jó része el is nyelődik, ezért nyilvánvaló, hogy a spallációs forrás ilyen felépítésben hatékonyabban "konvertálja" a nukleáris energiát neutronokká, tehát hatékonyabb neutronforrás, mint egy reaktor. (Sőt, nem beszéltünk még arról, hogy az ESS-ben átlagos fluxust számoltunk. Az impulzuscsúcsban körülbelül harmincszor nagyobb lehet a forráserősség!)

A feladat kérdezi még az évente elhasítandó urán mennyiségét. A másodpercenkénti hasadások számából ez könnyen adódik: 23,769 mol ²³⁵U mag hasad el azért, hogy biztosítsa az ESS nyalábjához szükséges energiát.

4. feladat (kitűzte: Papp Gergely)

Mi történne, ha a paksi reaktorokban a hűtésre és moderálásra szolgáló vizet nehézvízre cserélnénk? (A deutérium tömegét közelíthetjük a hidrogén tömegének kétszeresével.)

Megoldás: A feladat szövege utal rá, hogy a deutérium tömege szerepet játszik. Mint tudjuk a deutérium jobb moderátor mint a víz, mivel nem nyeli el a neutronokat. A kétszeres tömeg miatt azonban egy ütközésben átlagosan kevesebb energiát veszít a neutron, mint víz esetében. Ezért a lassulásig megtett út megnő. A paksi reaktorokban a fűtőelempálcák távolsága könnyű vízre van optimalizálva, ezért ha nehézvízzel töltenénk fel, akkor a neutronok még nem lennének termikusak, amikor elérik a következő fűtőelempálcát. Így a reaktorokat valószínűleg el sem lehetne indítani.

5. feladat (kitűzte: Papp Gergely)

Magyarország éves energiaigénye ~ 3 · 10¹⁰ kWh (mindenféle energia, nemcsak villamosenergia). Tegyük fel, hogy ennyi energiát tisztán szabályozott magfúzióból szeretnénk felszabadítani. A zárt rendszerben lejátszódó folyamatok: ⁶Li+n→He+T+4,8 MeV, D+T→ He+n+17,62 MeV. Itt D és T a deutériumot, illetve tríciumot jelzi. Számoljuk ki, hogy hány kg ⁶Li és hány liter nehézvíz lenne szükséges ehhez! Hány kg héliumgáz keletkezik? (A nehézvíz sűrűsége 1100 kg/m³.)

Megoldás: Az egy reakcióban összesen felszabaduló energia E_tot = (4,8+17,62) MeV = 2,242 · 10⁷ eV, azaz 3,592 · 10^-12 J. Mivel az energia megtermeléséről (és nem villamosenergia termeléséről) szól a feladat, ezért a hatásfok 100%. Az éves energiaigény 3 · 10¹⁰ kWh = 1,08 · 10¹⁷ J. Ebből látható, hogy évente 3,0 · 10²⁸ fúziós reakcióra van szükség. Ez A ~ 50 000 molnyi reakció. Egy fúziós reakcióhoz egy darab lítium atom és egy darab deutérium atom szükséges, és két hélium atom keletkezik. Tehát szükség van A mol ⁶Li-ra, A/2 mol D₂O-ra, és 2A mol He keletkezik. M_Li = 6, MHe = 4, M_D2O = 20. Tehát m_Li = 300 kg, m_He = 400 kg és V_D2O = 500/1,1 = 455 liter. (Nem kérdeztük, de a természetes lítiumban csak 7,6% a ⁶Li részaránya, így jóval több természetes lítiumra lenne szükség!)

6. feladat (kitűzte: Sükösd Csaba)

Az alábbi táblázat a természetes uránban előforduló uránizotópok néhány adatát tartalmazza:
________________________________________________
              izotóp                százalék                felezési idő
________________________________________________
              ²³⁸U                99,275                4,51 milliárd év
________________________________________________
               ²³⁵U                   0,72                0,71 milliárd év
________________________________________________
               ²³⁴U                0,0055                247 000 év
________________________________________________

1. Mennyivel csökken a fűtőanyag tömege 1 nap alatt?
2. Naponta mekkora tömegű kohókoksz elégetésével lehetne ezt a teljesítményt biztosítani?
3. Mekkora tömegű CO₂-dal szennyeznénk a légkört naponta a b) esetben számított kohókoksz elégetésével? (A kohókokszot tekintsük tiszta szénnek; égéshője 29,75 MJ/kg.)

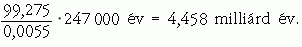
Megoldás: A maghasadásból származó teljesítmény 480/0,34 = 1411,76 MW. Ez egy nap alatt 1,2197 · 10¹⁴ J energia felszabadítását jelenti. Ezt elosztva c²-tel kapjuk, hogy a fűtőanyag tömege naponta 1,357 grammal csökken. Az egy nap alatt megtermelendő energiát elosztva a kohókoksz égéshőjével kapjuk, hogy naponta 4100 tonna kokszra lenne szükség. A széndioxid mennyiségét a moláris tömegek arányából kapjuk: 15 033,3 tonna CO₂ keletkezne.

8. feladat (kitűzte: Radnóti Katalin)

Ha a KI (káliumjodid) kristályból eltávolítunk egy jodid iont, akkor az üresen maradt helyet egy - ugyancsak negatív töltésű - elektron foglalhatja el ("elektronszíncentrum"). Ezt az elektront úgy tekinthetjük, mintha egy 2d oldalélű kocka alakú dobozba lenne bezárva, ahol d = 0,7 nm a KI-kristály rácsállandója. Milyen hullámhosszúságú fényt képes elnyelni a kristály?

Megoldás: A dobozba zárt elektron energiája:

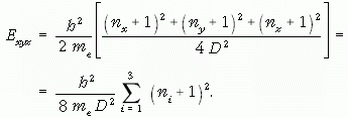
Itt D = 1,4 nm a kocka oldaléle, n_i az adott tengelyre merőleges csomósíkok száma, m_e az elektron tömege, és h a Planck-állandó. Vegyük a legegyszerűbb, E₀₀₀ →  E₁₀₀ átmenetet. Ekkor az első szumma értéke 6, a másodiké 3, tehát a keresett frekvencia

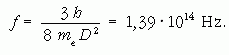
Ennek a hullámhossza:

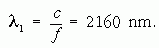
Ez még erősen az infravörös tartományba esik. A látható fény tartományába esne például az E₀₀₀ → E₃₀₀ átmenet, hiszen ekkor a szummák értékei 18 és 3, a különbség 15. Az ennek megfelelő hullámhossz értéke:

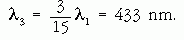
A folytatás a februári számban következik