A TISZTESSÉGES MAGATARTÁS KIALAKULÁSA: JÁTÉKELMÉLETI ELEMZÉS

Szabó György
MTA MFA

A játék nem játék

Az emberek és az állatok jelentős része játékokon keresztül sajátítja el, hogyan kell viselkedni azokban az élethelyzetekben, amelyekkel felnőtt korukban találkoznak. A legtöbb ilyen játék leegyszerűsített formában szembesíti a játékosokat a valóságban előforduló helyzetekkel. A leegyszerűsítés lehet olyan mértékű, hogy már a matematika nyelvét és eszközeit is használhatjuk a legjobb megoldás megtalálásában. A játékelmélet egységes matematikai keretének kidolgozását és ezen belül a játékok gazdag választékának osztályozását Neumann János indította el. A Neumann nevével fémjelzett klasszikus játékelméletben a játékosok önzőek (mindegyikük a saját nyereményének maximálására törekszik) és intelligensek, azaz mindegyikük ismeri az összes lehetséges döntést és az ahhoz tartozó számszerűsített nyereményeket. A játékosok intelligenciája arra is kiterjed, hogy ha létezik jó megoldás, akkor azt képesek megtalálni, miközben játékostársuk hasonló képességéről sem feledkeznek meg. Azt is tudják, hogy Ő tudja, hogy én tudom, hogy Ő .... A klasszikus játékelmélet erősen kötődik a közgazdaságtanhoz, mert az „üzleti élet” szereplőiről a játékosokhoz hasonló viselkedést lehetett feltételezni.

Az elmúlt évtizedekben a játékelmélet jelentős mértékben bővült és fejlődött. Kiderült, hogy az emberi viselkedés nem annyira racionális, amennyire azt a hagyományos játékelmélet feltételezi. Nagyon sok esetben a játék túl bonyolult - sok szereplő, ismétléses játékok, hiányos ismeretek, tévedések lehetősége stb. -, és ilyenkor a racionális gondolkodás helyett a társadalom tagjai egyszerű sémákat követve - például az eredményesebb szereplő viselkedésének utánzásával - próbálják maximalizálni saját nyereményüket. Ezt az utóbbi felismerést erősítette a biológiai evolúció matematikai megalapozása, ahol a játékelmélet alapfogalmát, a nyereménymátrixot használjuk a különböző stratégiákat képviselő fajok közötti kölcsönhatás jellemzésére, ami a fajok utódlétrehozó képességét (a sikerességét) számszerűsíti. A darwini evolúció alkalmazása a fajok egyedszámára azt jelenti, hogy a sikeresebb faj egyedei szaporodnak a sikertelenek kárára. A biológiai élet-halál játék szelídebb formában jelenik meg az emberi társadalmakban, ahol nem a sikertelen játékos pusztul ki, hanem csak a stratégiája, amikor átveszi a sikeresebb viselkedésformát.

A következő fejezetben egy olyan sokszereplős evolúciós játékelméleti modellt vizsgálunk, ami betekintést nyújt a tisztességes magatartás kialakulására az önző játékosok között is.

Társadalmi dilemmák

A legegyszerűbb társadalmi dilemma helyzetben két játékosnak, egymástól függetlenül kell arról döntenie, hogy a közösség számára előnyös C (cooperation) vagy az egyéni önzést képviselő D (defection) stratégiát választja. A döntésekhez tartózó számszerűsített nyereményeket egy bi-mátrix segítségével adhatjuk meg:

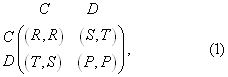
ami szerint mindkét játékos nyereménye R (Reward), ha C-t választottak, illetve P (Punishment), ha mindketten a D stratégiát követik. Ebben a szimmetrikus játékban a játékosok azonosak. Ez abban is megmutatkozik, hogy ellentétes választás esetén a D stratégiát választó játékos nyereménye T (Temptation to choose defection), míg ellenfelének nyereménye S (Sucker’s payoff) lesz. Az úgynevezett Fogolydilemma- helyzetekben a nyeremények sorrendje: T > R > P > S; a Szarvasvadászatnak megfelelő játékban: R > T > P > S; a Héja-Galamb játékban pedig: T > R > S > P.

Az említett játékok elnevezése is életből ellesett helyzetekre utal. A Fogolydilemmánál két játékosunk egymástól elkülönített cellában azon gondolkodik, hogy elárulja-e társát (D stratégia) vagy hallgasson (C stratégia). A rablási kísérlet után a tárgyi bizonyíték és szemtanúk hiánya miatt a rend őre azt ajánlotta nekik, hogy ők adjanak bizonyítékot társuk bűnösségére. Ha mindketten elárulják a másikat, akkor három hónapos börtönbüntetés szabható ki rájuk. Ha mindketten hallgatnak, akkor bizonyíték hiányában egy hét múlva kiszabadulnak. Azonnal szabadulhat az a játékos, aki egyoldalúan árulja el társát, aki viszont öthónapos büntetésre számíthat. Ebben az esetben nyereménynek tekinthetjük a maximális büntetéshez képest szabadlábon eltöltött időt. A Szarvasvadászat példája Rousseau-tól származik. Játékosaink a szarvas elejtésében csak akkor lehetnek sikeresek, ha mindketten kizárólag a vad elejtésére koncentrálnak (kölcsönös C), és a bekerítés közben egyikük sem próbálkozik az útjába eső kisvad (pl. nyúl) elejtésével (D stratégia), amit ugyan el lehet rejteni a társ elől, de ez a tevékenység biztosan elriasztja a nagyvadat. A nyereményt ekkor mérhetjük a várható zsákmány súlyával. Héja-Galamb játékkal osztozkodáskor találkozhatunk. A jutalom - ami lehet terület, vagy zsákmány, vagy pénz - elosztásánál játékosaink választhatják a békeszerető (C) vagy az agresszív (D) magatartást. Ha mindketten a C stratégiát választják, akkor felezik a jutalmat. Az agresszív játékossal szemben a békeszerető a teljes jutalmat átengedi. Két agresszív játékos azonban megverekszik a jutalomért és az egymásnak okozott sérülések mértéke meghaladja a jutalom értékének felét.

Mindhárom esetben a C kölcsönös választása nagyobb nyereményt biztosít a játékosok számára, mint a kölcsönös D (R > P), illetve, mint a C egyoldalú választása (R > S ). A játékosok mégis szívesebben választják a D-t, ha a D egyoldalú választása előnyösebb a kölcsönös C-nél (T > R), illetve, ha a kölcsönös D nagyobb jövedelmet biztosít, mint a D egyoldalú választása (P > S). Az előbbi feltétel teljesül a Héja- Galamb játékban, az utóbbi a Szarvasvadászatnál, és mindkét hajtóerő érvényesül a Fogolydilemmánál. A Fogolydilemma különlegessége, hogy a racionális (önző) játékosoknak D-t célszerű választani annak ellenére, hogy ezzel az össznyereményük értéke a lehető legkisebb lesz, amit a játékelméletben a Közösség Tragédiájának is hívnak. Más szavakkal, ez a játék mutatja meg legtisztábban, hogy az egyéni és közösségi érdekek között feloldhatatlannak tűnő ellentmondás alakulhat ki. Fogolydilemma-helyzet valósul meg akkor is, ha játékosainknak arról kell dönteni egymástól függetlenül, hogy befizetnek-e c költséget azért, hogy társuk b > c jövedelemhez jusson. A mindennapi életünkben ezen utóbbi helyzettel szembesülünk leggyakrabban, amikor például arról döntünk, hogy a munkamegosztásban számunkra kiosztott feladatot tisztességesen (C) vagy tisztességtelenül (D) végezzük el; a szakmánkat alaposan elsajátítjuk vagy sem; a közlekedésben betartjuk a szabályokat vagy tolakodunk, vigyázunk az egészségünkre vagy gyógykezelésünk költségeit másokkal fizettetjük meg stb. A felsorolt példák arra is utalnak, hogy egy társadalomban az erkölcsi válságnak, a szakértelem és közlekedési morál hiányának közös oka van: az egyéni önzés érvényesül a közösségi érdekkel szemben.

Felfedezése idején a Fogolydilemma létezése legalább akkora kételyeket okozott a kapitalizmus elméleti megalapozhatóságában, mint amit a püthagoraszi iskola hívei élhettek át akkor, amikor bebizonyították, hogy a 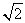nem racionális szám (a Fogolydilemmahelyzet felfedezőit nem végezték ki). Mára azonban számos magyarázatot és okot sikerült találni arra, hogy a tisztességes magatartás az önző egyének között is fenntartható a Fogolydilemma-helyzetekben. Az egyik fontos magyarázat a játék ismétlésére épül, ami kibővíti a játékosok lehetőségeit azáltal, hogy aktuális választásuknál figyelembe vehetik társaik korábbi döntéseit is. Robert Axelrod számítógépes versenye azt igazolta, hogy az ismétléses Fogolydilemma- játékoknál a Szemet-Szemért (vagy más néven Kölcsönkenyér visszajár, angolul Tit-for-Tat, röviden TfT stratégia használatával a közösség elkerülheti a tragikus végállapotot. A versenyben nyertes TfT stratégia az első lépésben C-t választ, majd pedig megismétli a játékostárs előző döntését, azaz D-vel bünteti a potyázást (vagy élősködést) és C-vel jutalmazza a tisztességes magatartást. Azóta is ez a javallott stratégia az egyén számára az ismételt Fogolydilemmahelyzetekben, ha játékostársainkról semmit sem tudunk. A következő fejezetben ugyanezt az eredményt egy olyan stratégiahalmaz segítségével elemezzük, ami további érdekességekre hívta fel a figyelmet.

Stochasztikus reaktív stratégiák versengése

A stochasztikus reaktív stratégiákat Martin Nowak és Karl Sigmund javasolta a sokszereplős ismételt Fogolydilemma elemzésére 1982-ben. A TfT hasonlatosságára a stratégiahalmaz stratégiái csak a partner előző döntését veszik figyelembe és a választott stochasztikus döntést két paraméter (0 < p, q < 1) jellemzi. A (p, q) stratégia p (illetve q) valószínűséggel választ C-t, ha a partner előzőleg C-t (illetve D-t) választott. Természetesen itt is meg kell mondani, hogy mi történjen az első lépésben, de hosszú távon ez a döntés elveszti a jelentőségét, ha 0< p, q < 1. Könnyű kiszámolni, hogy egy átmeneti időszak után a (p, q) és (p′, q′) stratégiák milyen valószínűséggel választanak C-t, illetve D-t egymás ellen és ugyanakkor a nyereményeik átlagos értékét is meghatározhatjuk.

A (p,q) stratégiák közül néhányat érdemes kiemelni. Az egyik legegyszerűbb stratégia (továbbiakban mD) feltétel nélkül választja a D-t, míg ellentétes pár- ja, az mC mindig a tisztességes magatartást követi. Ha p = q, akkor a játékosaink döntése független a partner előző választásától. Külön érdemes kiemelni a barátságos stratégiákat (p = 1), akik nem hajlandók elsőként élősködni partnereiken. A barátságos stratégiák együttműködnek, azaz egymás ellen mindig tisztességesek és közösségük számára a maximális össznyereményt biztosítják. Ezzel ellentétesen működnek azok a stratégiák, ahol q = 0, vagyis ők élősködni próbálnak egymáson és ennek hatására közösségük a társadalmi tragédia állapotába kerül. A korábban ajánlott TfT stratégia is része a stratégiahalmaznak. Az (1,0) determinisztikus reaktív stratégia többféle TfT stratégiát képvisel, attól függően, hogy mit választ az első lépésben. Az Axelrod versenyében nyertes stratégiák is barátságosak, vagyis segítik egymást. Ennek ellenére van egy hátrányos tulajdonságuk: szigorú magatartásuk következtében megbomolhat a közöttük kialakult együttműködés, ha bármiféle zavart követően egyikük tévedésből D-t választ. A hibás döntés után ellentétesen váltakozva választják a C és D döntéseket, aminek következtében átlagos nyereményük (T+S )/2 lesz, amiről feltételezzük, hogy kisebb, mint R. Már Axelrod felismerte, hogy ebből a zavarból kikerülhetnek a játékosok, ha az úgynevezett megbocsátó TfT -t (röviden mTfT) stratégiát, azaz az (1, q) stochasztikus reaktív stratégiát követik, ahol q a megbocsátás mértékét jellemzi. q = 1-nél az mTfT azonossá válik az mC stratégiával.

Nowak és Sigmund numerikusan vizsgálták, hogy mi történik egy olyan közösségben, ahol a végtelenül nagyszámú játékos ρ_i hányada követi az s_i = (p_i,q_i ) stratégiát, ahol a 100 különböző stratégiát véletlenül választották ki a lehetséges stratégiák közül. A t = 0 időpillanatban mindegyik stratégiát azonos számú játékos választotta [ρ_i (t=0) = 1/100]. Ezt követően a t = 1, 2, .... időpontokban a játékosok a replikátoregyenlet szellemében módosíthatták stratégiájukat, és a következő lépésben már a játékosok

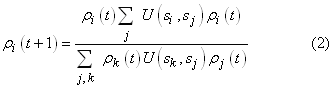
hányada választja az s_i stratégiát, ahol U (s_i, s_j) az s_i stratégiát követő játékos nyereményét fejezi ki az s_j -vel szemben. A jelenségek világosabb megjelenítése érdekében az 1. ábrán egy olyan időfejlődést mutatunk be, ahol a lehetséges 225 s_i stratégiát a kétdimenziós paramétertéren egyenletesen osztottuk el.

Az 1. ábra világosan mutatja, hogy kezdetben az mD stratégia jut a legmagasabb nyereményhez és emiatt követői elszaporodnak más, kevésbé élősködő (p,q = 0) stratégiákkal együtt. Ezzel párhuzamosan éltetőik, a jóhiszemű stratégiák zöme szinte teljesen kipusztul. A folyamat végén a játékosok nagy része a D döntést választja, vagyis a közösség eljut egy tragikus állapotba, ahol a közösség össznyereménye minimális. Ugyanakkor, a túlélő TfT stratégiák végig segítik egymást, nyereményük meghaladja az élősködő társakét, és emiatt a követők száma lassan növekedésnek indul, majd egy idő múlva ők uralják az egész rendszert. A rendszerben jelen levő zaj miatt azonban a TfT stratégiák gyakran büntetik egymást, és ekkor kezdenek elszaporodni az egyre megbocsátóbb mTfT stratégiát követő játékosok. Végül a stratégiapopuláció fejlődése leáll egy olyan állapotban, ahol a megbocsátás (q) elér egy optimális szintet.

A stochasztikus reaktív stratégiák lehetővé teszik, hogy a fent leírt jelenség okait analitikusan is értelmezhessük tetszőleges nyereménymátrix esetén. Meghatározhatjuk például azon stratégiák halmazát, amelyek a fenti folyamatban segítik az mD stratégiák szaporodását. Ezt jelöli a szürke tartomány a 2. ábrán olyan nyereménymátrix esetén, amit az 1. ábrán vázolt dinamikai folyamatban is használtunk. Kicsit több számolást igényel a vonalkázott terület meghatározása, ami azon stratégiákat jelöli, ahol kis mutációkon keresztül a homogén (p,q) stratégiapopuláció jobbra, illetve felfelé fejlődik. Más szavakkal, a rendszer számára előnyösebb, ha egy közeli homogén (p+δ,q) vagy a (p,q+δ) állapotba kerül. Az 1. ábrán vázolt fejlődési folyamat akkor áll le, amikor a vonalkázott tartomány felső  határának jobb szélén egy-egy alatta és felette elhelyezkedő stratégia dinamikai egyensúlyba kerül.

1985-ben Molander meghatározta a megbocsátás optimális mértékét egy olyan rendszerben, ahol a zaj (tévedés) gyakorisága tart a nullához. Eredményét a következő formula fejezi ki:

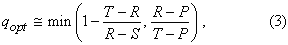
ahol a két feltétel egybeesik azokkal a q értékekkel, ahol a 2. ábrán vázolt határvonalak elérik a tartomány jobb szélét (p → 1 határeset). Az eredmény függése a nyereménymátrix értékeitől arra is magyarázatot ad, hogy miért volt nehéz feladat őseink számára a büntetés-megbocsátás optimális mértékének megállapítása egy olyan korban, ahol nem foglalkoztak döntéseik következményeinek számszerűsítésével. Itt érdemes felidézni, hogy a Biblia Ószövetség része a szigorú szemet-szemért fogatfogért elvet hirdeti (q = 0), ezzel szemben az Újszövetség a jézusi megbocsátás (q = 1) mellett szól.

A (3)-as képlet azt is jelzi, hogy a két feltétel közül a szigorúbbat kell figyelembe venni. Ez azért fontos, mert a két feltétel (határvonal a 2. ábrán) helyet cserél egymással, ha megfelelően változtatjuk a nyereménymátrix értékeit. Ebben az esetben a darwini evolúciós folyamat nem áll le egy homogén végállapotban. Amikor az egyre megbocsátóbb magatartásformák egymást követő uralmánál a megbocsátás mértéke eléri a szürke tartományt, akkor újra az mD stratégia élősködése lesz a legkifizetődőbb magatartásforma, és emiatt a közösség megint eléri a közösségi tragédia állapotát. Ezt az állapotot követi a szigorú TfT stratégiák uralma, majd a közösség az egyre megbocsátóbb magatartásformák felé fejlődik, aminek ismételten az mD uralom vet véget, és ez a körfolyamat ismétlődik a végtelenségig. Ezt a forgatókönyvet ismerhetjük fel a konfuciusi filozófia jin-jang szimbólumában, ami a sötétség és világosság - átvitt értelemben a Jó és a Rossz - örök körforgását képviseli.

Zárszó helyett

A játékelmélettel foglalkozó szakértők körében közhelynek számít, hogy a Fogolydilemma-helyzetekben az emberi társadalomban a büntetés vagy a büntetéstől való félelem tartja fent a tisztességes (közösségi érdeket előnyben részesítő) magatartást. A stochasztikus reaktív stratégiák körében a TfT stratégia képviseli a büntetést a játék ismétlődése esetén. A büntetésnek azonban számtalan egyéb módja is lehetséges a sokszereplős evolúciós játékoknál. Például, ha a közösség olyan törvényeket hoz, ami az egyéni nyeremény csökkentésével bünteti a közösségellenes magatartást, akkor ez a változtatás úgy módosíthatja nyereménymátrix értékeit, hogy az önző játékos számára is kikerülhető a dilemma. Egy másik lehetőséget képvisel a biológiában közismert csoportszelekció. Ebben az esetben a játékosok csoportokat alkotnak, és a sikertelen csoport kihalásán keresztül juthat előnyhöz a közösségi érdeket képviselő tisztességes magatartás. A csoportosulás (és ezen keresztül a büntetés) gyengébb formája jelenik meg térbeli evolúciós játékoknál, ahol a valóságos térben elhelyezkedő játékosok csak a közvetlen közelükben elhelyezkedő játékosokkal játszanak és a követendő viselkedést is lehetőleg ugyanebből a körből választják. Az elmúlt évek vizsgálatai arra világítottak rá, hogy a játékosok közötti különbözőség is segítheti a tisztességes magatartás kialakulását, ha felerősítjük annak hatását, hogy a C stratégiát követő mester-tanítvány párosok előnyt élveznek. Erről a történetről írunk majd a folytatásban.

Irodalom

1. K. Sigmund: Az élet játékai. Akadémiai Kiadó, Budapest, 1993.
2. M. A. Nowak: Evolutionary Dynamics: Exploring the Equations of Life. Harvard University Press, Cambridge, MA, 2006.
3. G. Szabó, G. Fáth: Evolutionary games on graphs. Phys. Rep. 446 (2007) 97-216.
4. R. Axelrod, W. D. Hamilton: The evolution of cooperation. Science 211 (1981) 1390-1396.
5. M. A. Nowak, K. Sigmund: The evolution of stochastic strategies in the prisoner’s dilemma. Acta Appl. Math. 20 (1990) 247-265.
6. P. Molander: The optimal level generosity in a selfish, uncertain environment. J. Conflict Resolut. 29 (1985) 611-618.
7. F. C. Santos, J. M. Pacheco, T. Lenaerts: Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl. Acad. Sci. USA 103 (2006) 3490-3494.