
Fizikai Szemle honlap |
Tartalomjegyzék |
Horváth Gábor
ELTE, Biológiai Fizika Tanszék
Az elefántok köztudottan nem képesek gazellák módjára szökdécselni. Vajon miként mozogtak a sokszor még az elefántnál is jóval nehezebb szárazföldi ősállatok, mint például a nagytestű dinoszauruszok? Az egyik elképzelés szerint túl gyengék lehettek a lábaik ahhoz, hogy roppant súlyukat megtartsák, így a tavakban élhettek, és a testüket a víz fölhajtóereje lebegtette. Mivel ezen ősállatok már réges-régen kihaltak, nem tehetünk mást, mint hogy a mozgásukat a csontmaradványaik és nyomfosszíliáik alapján próbáljuk meg rekonstruálni a ma élő állatok csontjainak és mozgásának vizsgálatával, a biomechanika alkalmazásával [1-6]. A biomechanika által föltárt tényeket összevetve a fosszilis csontokból és lábnyomokból kiolvasható adatokkal, kirajzolódik a válasz az ősállatok mozgékonyságának kérdésére. Megbecsülhetjük például, hogy a négylábú növényevő Triceratops vágtázhatott-e, vagy csak cammoghatott, és hogy a kétlábú ragadozó Tyrannosaurus képes volt-e utolérni egy menekülő Triceratopsot.
A dinoszauruszoknak többnyire csak a csontváza ismert (1. ábra bal oldala), amiből a hajdani magasságuk, hosszúságuk és megközelítő alakjuk határozható meg. A dinoszauruszok élőtömegének legnagyobb részét a bőrük, izmaik és belső szerveik tették ki, amelyek mára már régen elporladtak. Ezért a testtömegüket csak becsülni lehet, amihez arányosan kicsinyített dinoszaurusz- maketteket használnak a paleontológusok. E makettek olyanok, amilyennek a paleontológusok a kutatásaik eredményeiként a dinoszauruszokat elképzelik (1. ábra jobb oldala). A természettudományi múzeumokban és játékboltokban kapható dinoszauruszmodellek is e rekonstruált alakok alapján készülnek.
A kicsinyített dinomakettek térfogatát az általuk kiszorított víz térfogatából határozzák meg. Az így kapott értéket megszorozva a kicsinyítési tényező reciprokának köbével1, megkapják a vizsgált dinoszaurusz hajdani hozzávetőleges térfogatát. E térfogatot megszorozva a ma élő hüllők testének 1000 kg/m3 átlagsűrűségével, a dinoszauruszok testtömegének közelítő értékéhez jutnak. Ilyen becslések arra vezettek [3, 4], hogy például a húsevő Tyrannosaurus kifejlett tömege 7 tonnánál is nagyobb lehetett (egy felnőtt jegesmedve tízszerese), egy felnőtt növényevő Brachiosaurus pedig akár 50 tonnát is nyomhatott (tízszer akkorát, mint egy afrikai elefántbika vagy közel akkorát, mint egy ámbráscet).
A nagytestű szárazföldi állatok mérete, testi ereje és vázszerkezete közti kapcsolat mechanikai problémáját elsőnek Galilei vetette föl az 1600-as évek elején. Ha két mértanilag hasonló, azaz egy megfelelő mértékű N kicsinyítéssel/nagyítással egymásba vihető alakú állat lineáris méretei különbözőek, és lineáris kiterjedésük (pl. lábhosszuk) aránya L' /L = N, akkor a csontjaik keresztmetszetének aránya N 2 = A'/A, míg a súlyuké N 3 = G'/G. Ez azt jelenti, hogy az L' = N · L lineáris méret N szorzótényezőjének növekedésével a csontokban ébredő σ' = G'/A' = (N 3 · G)/(N 2 · A) = N · G/A = Nσ feszültség N-nel lineárisan nő. Ha tehát egy állat például N = 2-szer magasabb, szélesebb és hosszabb egy hozzá mértanilag hasonló másiknál, akkor 4-szer erősebb (azaz 4-szer nagyobb keresztmetszetű) lábaknak kell 8-szor nagyobb testsúlyt hordozniuk. Galilei ebből arra következtetett, hogy ha egy állat alakhasonlóan növekedne, akkor egy kritikus lineáris méret meghaladása után a saját súlyát már nem tudná megtartani, mert csontjai eltörnének, mikor a csontokban ébredő σ' = Nσ feszültség nagyobb a σ* törési (összeroppanási) feszültségnél. E megfontoláshoz fontos tudni, hogy a σ* értéke független a testmérettől, vagyis az N-szer nagyobb állat csontjai is ugyanakkora kritikus σ* feszültségnél törnek el, mint a kisebb állatéi.

Ha egy állat mozgási sebessége u, lábhossza L, a földi nehézségi gyorsulás pedig g, akkor az állat
Froude-száma f = u2/(gL), amit William Froude2
(2. ábra) angol hajómérnökről neveztek el. Mint ahogyan a mértani hasonlóság esetén a
két test alakja a hossz, szélesség és magasság azonos léptékű (N-szeres) megváltoztatásával egymásba képezhető le,
úgy két különböző test mozgása akkor hasonló dinamikailag, ha a Froude-számuk azonos. Ekkor az egyik test lineáris méreteinek
és az általa megtett útnak azonos léptékű (N-szeres) megváltozása mellett létrejövő mozgás előidézéséhez szükséges
erő a két mozgás Froude-számának megegyezéséből határozható meg, s az ilyen mozgások egymásba dinamikailag átvihetőek.
Nézzünk erre egy egyszerű példát: a g nehézségi gyorsulású földi gravitációs térben gyorsítsunk függőlegesen fölfelé egy
R sugarú, homogén ρ sűrűségű, m = 4πρR3/3 tömegű gömböt.
Az ehhez szükséges erő
F = m · (g +
a). (1)
ahol a a test fölfelé mutató gyorsulása. Ha a test kezdősebessége nulla, akkor az általa megtett s út és az u sebesség közti összefüggés

a test Froude-száma pedig

A (1), (2) és (3) fölhasználásával kapjuk:
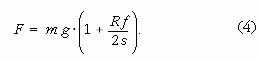
Ha ezek után egy ugyancsak ρ sűrűségű, de N-szer nagyobb sugarú másik gömb dinamikailag hasonló mozgását tekintjük, akkor a gömb R' sugara, m' tömege és az általa megtett s' út a lineáris méretek N-szeres skálázása miatt
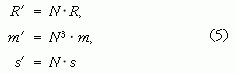
lesz, az ehhez szükséges erő pedig
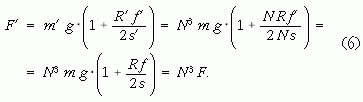
Mivel a dinamikai hasonlóság miatt a két mozgás Froude-száma egyenlő: f ' = f. Tehát ha a szóban forgó függőlegesen gyorsuló gömb és annak mozgása lineáris méreteit N-szeresére növeljük, akkor a két mozgás akkor lesz egymáshoz dinamikailag hasonló, ha a gyorsításhoz szükséges, fölfelé irányuló erő N3-szeresére nő. Annak idején Froude hasonló, bár ennél bonyolultabb számítással határozta meg, hogy mennyivel kell szorozni a hajómakettjein mért tolóerőket, hogy megkapja a valódi méretű hajók valós mozgásaihoz szükséges tolóerőket.
Visszatérve az állatokhoz, két állat mozgása csak akkor lehet dinamikailag hasonló, ha az m tömegű, u átlagsebességű és L hosszúságú lábaik mu2/2 mozgási és mgL/2 helyzeti energiájának u2/(gL) hányadosa azonos, ami nem más, mint éppen az f Froude-szám. Ennek megfelelően két eltérő méretű állat mozgása akkor hasonló dinamikailag, ha a Froude-számuk megegyezik. Alexander [2-4] vetette föl először, hogy a különböző méretű állatok járásmódja, mozgása dinamikailag közel hasonló, ha a mozgásuk Froude-számai azonosak. Teljes dinamikai hasonlóság azért nem teljesülhet, mert az eltérő méretű állatok általában alakjukban is különböznek egymástól. Teljes dinamikai hasonlóság csak szigorú geometriai hasonlóság esetén állhat fönn.
Alexander [2-4] elmélete szerint az egyforma Froude-számú, de különböző méretű állatok hasonló módon járnak vagy futnak. Például az Lmenyét = 9 cm csípőmagasságú menyét umenyét = 1,5 m/s sebességnél vált át ügetésből gyors futásba, mikor is a Froude-száma fmenyét = 2,55, míg az Lorrszarvú = 1,2 m csípőmagasságú orrszarvú uorrszarvú = 5,5 m/s sebességnél vált poroszkálásból ügetésbe, mikor a Froude-száma forrszarvú = 2,57. Látható, hogy fmenyét ≈ forrszarvú.
Az elmélet a lépéshosszra, azaz egyazon láb két egymást követő nyomának s távolságára is érvényes (3. ábra). Minél gyorsabban halad egy állat, annál hosszabbakat lép. A különböző méretű, de azonos Froude-számú állatok s lépéshossza és L lábhossza a dinamikai hasonlóság folytán hasonlóképpen aránylik egymáshoz. Ebből következően, ha az r = s /L relatív lépéshosszat az f Froude-szám függvényében ábrázoljuk különféle két- és négylábú állat esetén, akkor mindig ugyanazt a függvényt kapjuk. Ezt szemlélteti a 4. ábra, ahol az (r, f) paraméterpár számos állaton mért értékei vannak föltüntetve. Látható, hogy az (r, f) koordinátájú pontok halmaza jó közelítéssel ugyanazt az r (f) függvényt követi.
Mindez azonban csak a házimacskánál nem kisebb méretű állatokra érvényes, mivel akisebb állatok (pl. az egerek, pockok és patkányok) sajátosan a földhöz lapulva mozognak. Érdekes módon azonban az elmélet érvényes mind a kétlábú, mind a négylábú állatok mozgására. Ez nem is olyan meglepő, ha meggondoljuk, hogy egy négylábú állat lényegében egy mellső és egy hátsó lábpárból és a kettőt összekötő vízszintes törzsből épül föl, amely végtagok megfelelően szinkronizálva, bizonyos fáziskéséssel, de ugyanúgy mozognak, legalábbis a szimmetrikus járásmódok esetében.
Az Alexander [2-4] által a ma élő két- és négylábú állatokon tapasztalatilag megállapított r (f) függvény (4. ábra) lehetőséget ad arra, hogy megbecsülhető legyen a réges-régen kihalt dinoszauruszok mozgássebessége a megkövült lábnyomaik alapján. Igen sok dinoszaurusz-lábnyom maradt fönn fosszilizált iszaplenyomatok formájában (5. ábra) [1, 5]. E lábnyomok szerint járás közben a dinoszauruszok lába a testüket folyamatosan a magasban tartotta a ma élő emlősökhöz és madarakhoz hasonlóan, s nem úgy, mint a mai hüllőknél, amelyek lába oldalra nyúlik ki, miáltal törzsük többnyire a földhöz ér. Föltételezve, hogy a mai emlősökre és madarakra megállapított r(f) függvény (4. ábra) érvényes a hozzájuk hasonlóan járó dinoszauruszokra, az utóbbiak mozgássebessége a következő módon becsülhető meg: Alexander [2-4] ugyancsak empirikus úton jutott arra az összefüggésre, hogy az állatok lábának L hossza a talplenyomatuk d átmérőjének közel 4-szerese: L ≈ 4d. A dinoszauruszok megkövült járásnyomaiból (5. ábra) egyértelműen meghatározható a lábnyomuk d átmérője és lépésük s hossza (4. ábra), innen pedig az L ≈ 4d összefüggésből az L lábhossz is. Az így adódó r = s /L ≈ s /(4d) relatív lépéshossz ismeretében az r (f) függvény inverzéből megkapjuk az f [r ≈ s /(4d)] = u2/(gL) ≈ u2/(4gd) Froude-számot, ahonnan végül az
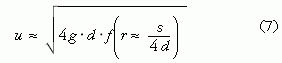
becsült mozgássebességhez jutunk.
Alexander [2-4] ilyen rekonstrukciói szerint a nagytestű dinoszauruszok meglehetősen lassan jártak, amikor lábnyomaikat az iszapban hagyták. A négy lábon járó hatalmas szauropodák összes ismert lábnyoma 1 m/s körüli mozgássebességre utal, ami az ember gyaloglás közbeni sebessége. A két lábon járó nagy dinoszauruszok mozgássebessége sem lehetett nagyobb, mint 2,2 m/s, ami az ember szaporázó járásának felel meg. A kistestű dinoszauruszok viszont gyorsabban közlekedtek: a legnagyobb sebességet, 12 m/s-ot egy kétlábon járó dinoszaurusz hagyta az iszapban. Ez már gyorsabb mozgás, mint amit a legjobb gyorsfutó emberek el tudnak érni, akik 10 m/s maximális sebességre képesek.
A mozgássebesség megkövült iszaplábnyomok alapján rekonstruált értéke azonban alulbecsüli azt a legnagyobb sebességet, amelynek elérésére a dinoszauruszok képesek lehettek. Ennek az az oka, hogy a nedves, puha, csuszamlós iszapban nyilván csak kisebb sebességgel közlekedhetnek az állatok, mint a kemény, nem csúszós szárazföldön. Ezért a dinoszauruszok nagyobb sebességű mozgásának vizsgálatához a Froude-számra és a fosszilizálódott lábnyomokra a lapuló módszertől eltérő rekonstrukcióhoz kell folyamodni.
Minél nagyobb sebességgel mozog egy állat, annál nagyobb erőt fejt ki lábával a talajra, ami annál nagyobb erővel hat vissza a lábra. A nagyobb sebesség eléréséhez tehát erősebb lábak szükségesek. A sebesség növekedésével a lábak a teljes lépésidő egyre kisebb részében érintik a talajt. A lépés kiegyensúlyozottsága és a testsúly megtartása érdekében ezen rövid idő alatt a lábaknak nagy erőt kell kifejteniük. Azt a legnagyobb erőhatást, amely a lábnak a talajjal való érintkezése közben föllép, csúcserőhatásnak nevezik. Az emberi lábon mérhető csúcserőhatás például lassú járás közben megközelítőleg a testsúllyal egyenlő, vágtázáskor azonban a testsúlynak akár 3,5-szerese is lehet. A gyors futás tehát erősebb csontozatot igényel.
Alexander [2-4] különféle állatok (pl. kutya, birka, ember, kenguru) eltérő mozgásformája (pl. gyaloglás, futás, szökellés) esetén laboratóriumi kísérletekben (miközben az állatok a padlóba ágyazott nyomásérzékelő lemezen mozogtak) meghatározta a lábcsontokban ébredő erőket. A csont két végén, az ízületeknél föllépő erők mechanikai feszültséget keltenek a csontban. Ezen erők két összetevőre bonthatók: a csont hossztengelyének irányában, a végektől a középpont felé mutató Ft tengelyirányú erőre és az erre merőleges, Fk keresztirányú erőre a 6. ábra szerinti módon. Az Ft erőkomponens a csont A keresztmetszetén σt = Ft/A nyomófeszültséget hoz létre. Az Fk összetevő a csontvégtől x távolságban σk = Fk x/I keresztirányú feszültséget kelt, ahol I a csont keresztmetszetének másodrendű nyomatéka, más néven felületi tehetetlenségi nyomatéka.
Túlságosan nagy mechanikai feszültségek hatására a csont eltörik, megreped. Futó és ugró mozgás közben σt << σk. Tehát mozgás közben a keresztirányú erők a csontokra sokkal veszélyesebbek a tengelyirányúaknál. Ezért a további becslések során csak a σk feszültséggel számolunk. A különböző méretű, de dinamikailag hasonló módon futó állatok esetében a csontokra ható erők a G testsúllyal arányosak, hiszen az állat testsúlyát mozgás közben a csontoknak kell megtartaniuk. A szóban forgó x távolság nyilván nem lehet nagyobb, mint a csont L hossza. Tehát σk ≤ σk* ~ aGL/I, ahol az a tényező azt fejezi ki, hogy a testsúly hányad része jut az adott lábpárra. Az
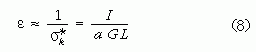
mennyiséget erőindikátornak nevezzük. Alexander [2-4] elmélete szerint, minél nagyobb egy állat csontjainak ε erőindikátora, annál mozgékonyabb az állat, vagyis annál nagyobb sebességekre képes, röviden, annál "atlétikusabb" mozgású. Ez azzal magyarázható, hogy egy adott csont ε erőindikátora akkor nagy, ha az I felületi tehetetlenségi nyomatéka nagy és/vagy az L hossza kicsi és/vagy a viselendő aG súly kicsi. Márpedig egy csont annál jobban ellenáll a mozgás közbeni erőhatásoknak, minél nagyobb az I -je. Továbbá minél rövidebb egy csont és minél kisebb erőhatás éri (súly terheli), annál kevésbé hajlik meg. Az ilyen csontokkal rendelkező állatok ezért nagyobb sebességgel, dinamikusabban mozoghatnak, mert csontjaik még az ekkor föllépő nagyobb mechanikai terheléseket is törés nélkül tudják elviselni. Alexander [2-4] meghatározta számos ma élő állat hosszú lábcsontjainak ε erőindikátorát és vizsgálta a különféle mozgásformáikat is, és arra a következtetésre jutott, hogy a hasonló erőindikátorú csontozattal bíró állatok hasonló mozgásformákra képesek. Ezek után meghatározta a dinoszauruszok fő lábcsontjainak erőindikátorát is. Néhány eredményt a 7. ábra mutat.
Mindezek alapján - föltéve, hogy a dinoszauruszok csontjai is ugyanakkora mechanikai feszültség elviselésére voltak képesek, mint a mai állatokéi - biomechanikailag alátámasztott becslések tehetők a dinoszauruszok mozgástípusairól. Ehhez persze még föl kell tételezni, hogy az evolúció során a különféle állatok csontjaiba ugyanakkora biztonsági faktor épült be. A biztonsági faktor a csont összeroppantásához szükséges erő és a csont rendeltetésszerű használata során föllépő maximális erő hányadosa. A mérnöki gyakorlatban 2-nél nem kisebb biztonsági faktort szokás használni.
Alexander [2-4] megbecsülte különféle dinoszauruszfajokra az a paraméter értékét is, vagyis a testsúly mellső és hátsó lábpárok közti megoszlásának mértékét. Ehhez megint a korábban már említett műanyag dinomaketteket használta: a makettekből a ma élő állatok anatómiája alapján becsült térfogatú tüdő helyén eltávolította a műanyagot (miáltal a helyét levegő töltötte ki), majd cérnára való fölfüggesztésekkel3 meghatározta az így preparált makettek tömegközéppontjának helyét, aminek ismeretében arányos osztással megkapta az a paraméter értékét.
Ilyen vizsgálatokkal derült fény például arra, hogy a hatalmas testű növényevő Apatosaurus lábcsontjainak εApatosaurus = 6-14 erőindikátora közel esik a jóval kisebb afrikai elefánt lábcsontjainak εelefánt = 7-11 erőindikátorához. Következésképpen, a nagyobb testméret ellenére is az Apatosaurus mozgékonysága az elefántéhoz lehetett hasonló (8. ábra). Az elefánt lassú futásra még képes, de vágtázni vagy ugrani már nem tud. Valószínűleg ugyanez volt a helyzet az Apatosaurus esetében is. Ahhoz, hogy az elefánténál hosszabb lábú Apatosaurus mozgása egy 5 m/s sebességgel haladó elefántéval azonos Froude-számú legyen, az Apatosaurusnak 7 m/s-mal kellett volna haladnia.
Az is kiderült, hogy habár a Diplodocus szauropoda nem lehetett túl mozgékony állat, mégsem szorult rá a víz fölhajtóerejére, és képes lehetett a szárazföldön is közlekedni, de futni valószínűleg már nem tudott. A Triceratops erőindikátor-értékei az elefántéi és a nála is mozgékonyabb kafferbivalyéi közé esnek, ezért a Triceratops mozgékonyabb lehetett az elefántnál, valószínűleg képes volt vágtázni is, akár a kafferbivaly vagy az orrszarvú (9. ábra).
A két lábon járó Tyrannosaurus combcsontjának (femur) ε erőindikátora kicsi volt, körülbelül az elefánténak felelt meg (7. ábra), következésképpen csak olyan lassan és úgy mozoghatott, mint az elefánt.
Habár a dinoszauruszok mozgásának és mozgékonyságának fönt vázolt paleo-biomechanikai rekonstrukciója becslés jellegű, azt mégis világossá teszi, hogy a dinoszauruszok általában lassan közlekedtek, de néhányuk meglehetősen gyorsan is tudott futni, és egyiküknek sem volt szüksége arra, hogy kihasználja a víz fölhajtóerejét. A dinoszauruszok megkövült lábnyomaiból úgy tűnik, hogy ha mi emberek már éltünk volna a dinoszauruszok korában, és ha lett volna hozzá bátorságunk, akkor akár sétálgathattunk is volna a mozgó Apatosaurusok vagy Tyrannosaurusok mellett, minden nehézség nélkül lépést is tarthattunk volna velük, sőt futva könnyen el is tudtunk volna menekülni előlük, mivel e nagytestű őshüllők legföljebb csak olyan mozgékonyak lehettek, mint az afrikai elefántok.
Steven Spielberg4 Jurassic park című híres tudományos fantasztikus filmtrilógiájában számos dinoszaurusz mozgásának számítógépes animációja és szimulációja is látható. E filmekben talán a legizgalmasabbak azok a jelenetek, mikor a főhősöket egy Tyrannosaurus rex üldözi. A film szerint a Tyrannosaurus még arra is képes, hogy üldözzön és utolérjen egy gyorsuló terepjárót vagy egy viszonylag gyorsan haladó nagyvárosi buszt, arról nem is beszélve, hogy simán el tudja kapni az előle futva menekülő embereket (10.a ábra). Az ebben a fejezetben tárgyalt paleo-biomechanikai tények és rekonstrukciók alapján azonban nyilvánvaló a mozgó Tyrannosaurus ilyen ábrázolásának pontatlansága: a Tyrannosaurus nemhogy egy nagy sebességű buszt vagy terepjárót nem lett volna képes utolérni, de még az ember is könnyen el tudott volna futni előle. Ha viszont a filmben így ábrázolták volna-e nagytestű, vérengző ragadozó őshüllőket, nyilván nem lett volna a film olyan borzongató.
Hasonlóan hibás például a Jurassic park II. azon jelenete is, mikor egy, a kölykét féltő feldühödött Apatosaurus utolér egy előle futó embert, aki csak egy korhadt, kidőlt fatörzsbe bújva lel menedéket. Ugyancsak hibás például a Jurassic park III. film azon jelenete, amelyben egy Spinosaurus egy előle menekülő embercsoportot üldöz (10.b ábra). Az Apatosaurus és a Spinosaurus a Tyrannosaurushoz hasonlóan nem volt képes még olyan gyorsan sem futni, mint egy rohanó ember.
Habár a Jurassic park filmekbeli dinoszauruszok mozgásának tudományos hűsége kívánnivalót hagy maga után, ezt részben kompenzálhatja, hogy e dinoszauruszok számítógépes szimulátorai jónéhány tudományos, részben mozgásmechanikai tényt is fölhasználtak, amelyek zömét Alexander és kollégái tárták föl.
____________________________