BIZTOS-E, HOGY AZ ENERGIA MEGMARAD?

Hraskó Péter
PTE Elméleti Fizika Tanszék

Mielőtt megpróbálnánk válaszolni, pontosítsuk a kérdést: elegendőek-e az empirikus tények (megfigyelések) ahhoz, hogy teljes bizonyossággal levonhassuk belőlük az energia megmaradását. Ha ebben a szellemben értjük valaminek a bizonyosságát (nevezzük ezt empirikus bizonyosságnak), a kérdésünkre csak tagadó választ adhatunk, mert elszigetelt, egyedi tényekből sohasem lehet általános érvényű következtetést levonni. A bizonyosságnak ilyen szigorúan aszkétikus értelmezéséhez tartva magunkat csak megtörtént egyedi tényeket tekinthetnénk biztosnak. Elengedtem ezt a krétadarabot és leesett a földre. Biztos, hogy leesett? Erre válaszolhatjuk, hogy biztos, mert mindannyian láttuk, tapasztaltuk. De most nézzük ezt a kijelentést: Ha a földön állva elengedek egy krétadarabot, biztos, hogy le fog esni. A mindennapok gyakorlatában és a tudományos praxisban is ezt természetesen szintén igaz állításnak tekintjük, de ezzel túllépünk az empirikus bizonyosság szabta korlátokon, hiszen abból, hogy egy elengedett tárgy eddig mindig leesett, logikai alapon nem következtethető ki, hogy ezentúl is mindig le fog esni.

Ez az egyszerű példa mutatja, hogy ítéleteinket, viselkedésünket, elvárásainkat a bizonyosságnak valójában tágabb fogalmára alapozzuk, mint az empirikus bizonyosság, mert bizonyosnak tekintjük, hogy ami eddig már nagyon sokszor kivétel nélkül mindig bekövetkezett, ezután is be fog következni. Ha tehát tekintettel akarunk lenni az emberi gyakorlat követelményeire is, a bizonyosságnak az empirikusnál általánosabb fogalmával kell operálnunk.

Nevezzük ezt a tágabb jelentésű bizonyosságot induktív bizonyosságnak, mert azt a fajta érvelést, amely az egyedi esetekből az általános törvényszerűségre következtet, induktívnak szokás hívni, és térjünk újra vissza a címben feltett kérdésünkhöz: biztos-e, hogy az energia megmarad. Az induktív bizonyosságot tartva szem előtt azt kell mondanunk, ha igaz az, hogy nagyszámú eddigi tapasztalatunk szerint az energia kivétel nélkül mindig megmaradt, akkor az energiamegmaradást biztosnak tekinthetjük. De amikor az energiamegmaradást a szabadesés előbb tárgyalt példájával összehasonlítjuk, tárgyilagosan el kell ismernünk, hogy a két eset között óriási fokozatbeli különbség van: az elejtett tárgyak zuhanását nap mint nap folyamatosan megfigyeljük, míg az energiamegmaradás nagypontosságú ellenőrzése speciálisan megtervezett kísérletet igényel.¹ Magának az energiának a fogalmával is csak az iskolában ismerkedünk meg, nem tapad hozzá olyan érzékletes tapasztalatunk, mind a szabadeséshez. Az energiamegmaradást igazoló kísérleteknél továbbá elkerülhetetlenül előjön a mérési pontosság kérdése is, és olyan megfigyelés biztosan nem létezik, amely az energiamegmaradást abszolút pontossággal (mérési hiba nélkül) igazolta volna.

Arra a következtetésre jutunk tehát, hogy amikor a fizikusok azt állítják, hogy az energiamegmaradás az egyik legjobban megalapozott természeti törvény, ezen nem az induktív bizonyosságot értik. A természettudománynak abból az életszerű gyakorlatából indulnak ki, amely a természettörvényekre vonatkozóan a bizonyosság helyett a plauzibilitás (hihetőség, elfogadhatóság) fogalmával operál, és felismeri, hogy a plauzibilitásnak fokozatai vannak: egy fizikai törvény lehet rendkívül plauzibilis, közepesen vagy kevéssé plauzibilis. A beszédmódot világosabbá tehetjük, ha a plauzibilitás mértékét a (0, 1) intervallumba eső számmal fejezzük ki úgy, hogy az 1-et a biztos érvényességhez, a 0-t a biztos érvénytelenséghez rendeljük. A feladatunk tehát az, hogy megvizsgáljuk, milyen alapon minősítik a fizikusok az energiamegmaradást egészen különlegesen plauzibilis törvénynek, vagyis miért rendelnek hozzá az 1-től alig különböző plauzibilitás értéket.

Az energiamegmaradás mellett szóló érveket öt csoportra lehet osztani:

• Minden eddig tervezett és elkészített örökmozgó működésképtelen volt;
• A tétel előre nem látott kritikus szituációkban is a megoldás kulcsának bizonyult;
• Egy sor atomfizikai kísérlet alapul az energiamegmaradás nagyon pontos teljesülésén;
• Az elvnek kulcsszerepe van fontos technikai alkalmazásokban;
• Az energiamegmaradás a mechanikában és az elektrodinamikában levezethető a Newton-egyenletből és a Maxwell-egyenletekből, sőt elméletileg sikerült megmutatni, hogy ez a törvény mindig érvényes, amikor a körülmények időben nem változnak.

A továbbiakban ezeket az érveket vizsgáljuk meg. A negyedikre azonban nem térünk ki külön, mert a példák (hőerőgépek, robbanó motorok, elektromos hálózatok és berendezések stb.) közismertek. Ezek a példák külön-külön talán nem tekinthetők az energiamegmaradás nagypontosságú igazolásának (mert a pontatlanul kontrollált veszteségek miatt csak azt bizonyítják, hogy az energia magától nem nő), összességükben mégis nagyon erős érvet szolgáltatnak mellette.

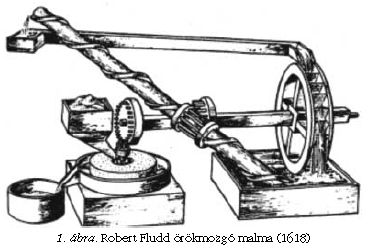
Tudomásom szerint perpetuum mobiléről először egy i. sz. 5. századi szanszkrit kéziratban történik említés. A kézirat leírja, hogy ha egy nagy kerék peremén megfelelően kialakított zárt kamrákat higannyal töltünk meg és a kereket forgásba hozzuk, akkor örök időkig forogni fog (a kéziratban nincs rajz). Az örökmozgók fénykora azonban ezer évvel később, a reneszánszban jött el. Rengeteg terv maradt ránk, a legismertebb talán Robert Fludd szerkezete 1618-ból (1. ábra), amely az archimedesi csavar vízfelemelő képességén alapul. De az éleselméjű szerkezetekkel párhuzamosan erősödik az a meggyőződés is, hogy ezek "csak papíron" működnek, a valóságban nem. John Wilkins püspök (1614-1672), aki a Royal Society egyik alapítója volt, meg is konstruált néhányat a javasolt örökmozgó szerkezetek közül. Megállapította, hogy egyik sem működik és arra a határozott következtetésre jutott, hogy örökmozgó nem létezhet. Száz év múlva a tudományos világ ezt már annyira biztosnak tekintette, hogy a Francia Tudományos Akadémia 1775-ben elhatározta, többet nem foglalkozik perpetuum mobilét tartalmazó beadványokkal. Az USA Szabadalmi Hivatala a 20. század elején ennél valamivel engedékenyebb volt: hajlandó volt foglalkozni örökmozgóra vonatkozó tervekkel, de csak azzal a feltétellel, ha azok zárt helyiségben legalább egy éven keresztül működtek. Mindeddig egyetlen ilyen találmányt sem nyújtottak be.

A sok sikertelenpróbálkozás hatására a természetkutatókban és a feltalálókban fokozatosan kialakult az az intuíció, hogy ha a szerkezetet külső forrás (szél, vízáram, tűz) nem táplálja, akkor hamarosan leáll, mintha valami "elfogyna" belőle. Ez a valami, ami "elfogy", az energia első homályos, kvalitatív fogalma. Elsőként a mechanikában sikerült tisztázni az energia pontos mibenlétét. De ehhez először precízen meg kellett fogalmazni, hogy mit értünk "munkán". Ez a 19. század elejére tisztázódott: Az út × erő szorzatra a "munka" nevet először J. V. Poncelet használta 1826-ban. Az is kiderült, hogyan lehet egy mechanikai rendszerről "ránézésre", a paramétereinek pillanatnyi értéke (vagyis a rendszer állapota ) alapján megmondani, mennyi energia van benne. A rendszer energiája az egyes elemek mozgási és helyzeti energiájának az összegével egyenlő, és ezek kiszámítására konkrét képletek állnak rendelkezésünkre. Kiderült tehát, hogy az energia (E) a rendszer állapotának meghatározott függvénye,² és a rendszeren végzett munka (A) arányában nő, a rendszer által végzett munka arányában pedig csökken. Ha a rendszeren végzett munkát pozitívnak, a rendszer által végzett munkát pedig negatívnak tekintjük, ez a két állítás a következő képletben foglalható össze:

A munkagép csak akkor működhet folyamatosan, ha valamilyen külső ágens a rendszer állapotát³ (és ezzel az energiáját) állandóan fenntartja.

Első látásra ez a képlet nem azt fejezi ki, hogy az energia megmarad, hanem azt, hogy vagy lecsökken (A < 0, ha egy munkagép energiájáról van szó), vagy megnő (A > 0, ha a munka tárgyára vonatkoztatjuk). Azonban a munkavégzésben mindkét résztvevő egyaránt jelen van, és ha mindkettőt figyelembe vesszük, a képletből leolvashatjuk, hogy az energia megmarad, csak éppen átkerül a munkagépről a munka tárgyára. A munkagépből és a munka tárgyából álló teljes rendszer 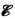energiája tehát megmarad:

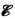 = konstans        (2)

Az energiamegmaradásnak ez a teljesen explicit formája kevésbé részletező, mint (1), de sok esetben éppen emiatt hatékonyabb: akkor is alkalmazható, amikor nem ismerjük azt a mechanizmust, amelynek révén az energia a rendszer egyik részéből átadódik a másikba.

Szigorúan véve a perpetuum mobile lehetetlenségéből is csak annyi következik, hogy az energia "magától" sohase nő, de azzal még összeférhetne, hogy folyamatosan csökken. A mechanika newtoni axiómái alapján azonban bebizonyítható, hogy a mechanikai jelenségek körében megmarad. Hosszú tévelygések után csak a 20. század elején vált általánosan elfogadottá, hogy az atomisztika alapján ez a kép a gázokra, folyadékokra és a szilárd közegekre is alkalmazható és ezek energiája szintén kiszámítható az állapotuk alapján, amelyet most a hőmérsékletük is jellemez. Egy mólnyi egyatomos ideális gáz energiáját például az

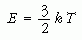
képlet határozza meg. Világossá vált, hogy a rendszer állapotát nemcsak a munka, hanem a hőátadás (Q) is megváltoztatja.⁴ Ha a rendszer által felvett hőt tekintjük pozitívnak, az (1) képletet így általánosíthatjuk:

A 20. század elejére általánosan elfogadottá vált, hogy a fizika akkor ismert ágaiban (a mechanikában, a termodinamikában, az elektrodinamikában, sőt az élő szervezet anyagcseréjében is⁵) az energia megmarad. Ennek ellenére, a század első harmadában mégis bekövetkezett három olyankritikus pillanat, amelyben ez a hit megingott, mert úgy tűnt, hogy bizonyos tapasztalati tényeket lehetetlen összhangba hozni az energiamegmaradással.

A radioaktív hő eredete - az E = mc² képlet

1903-ban Pierre Curie kimutatta, hogy egy rádium minta minden grammja óránként annyi hőenergiát ad le, amennyi 140 gramm víz hőfokát 1 fokkal tudja megemelni. Ez kereken 600 J, amely 60 kg tömeg 1 méter magasra történő felemeléséhez elég. Akkoriban már sejtették, hogy a radioaktivitás az atomok átalakulásával jár együtt, és néhány évvel később már tudták, hogy bomlás sémája ₈₈Ra²²⁶ → ₈₆Rn²²² + α. A minta állapota tehát változik, de a probléma az volt, hogy az energia akkor ismert képletei között nem akadt olyan, amely ehhez az állapotváltozáshoz tartozott volna. Komolyan latolgatták azt a lehetőséget, hogy a radioaktivitás akkor még szinte teljesen ismeretlen világában az energia nem marad meg.

1905 szeptemberében publikált cikkében Einstein a relativitáselméletből kiindulva levezette az E = mc² képletet és ezzel megmutatta, hogy a tömeg az energia egy formája. A cikke legvégén pedig megjegyezte, hogy a radioaktív bomlásban keletkező hő ezzel magyarázatot nyer, mert az E-be bele kell érteni a tömegben rejlő energiát is.⁶

Ebben az esetben célszerű az energiamegmaradás (2) formájából kiindulni. Az adott esetben ez azt fejezi ki, hogy a nyugvó rádium atom m_Rac² energiája egyenlő a bomlástermékek tömegében rejlő energiának és mozgási energiájuknak az összegével:

A bomlástermékek tehát (m_Ra - m_Rn - m_α) c² nagyságú mozgási energiával rendelkeznek, és ennek jelentős része hővé alakul, miközben lefékeződnek. A radioaktív bomlás során kiváló hő tehát nem azt bizonyítja, hogy az energiamegmaradás sérül, hanem - éppen ellenkezőleg - annak következménye, hogy az energia még ebben a vadonatúj jelenségkörben is megmarad.

Az atomok és a fény kölcsönhatása

A fotonhipotézis története különös élességgel világít rá az energiamegmaradás univerzalitására és jelentőségére.

Einstein 1905-ben posztulálta a fénykvantumok létezését. Észrevette, hogy a fotoeffektus paradoxálisnak látszó törvényei könnyen megmagyarázhatók az energiamegmaradás alapján, ha feltételezi, hogy a fénysugárban az energia hν nagyságú kvantumokban terjed. Ekkor a kilépő elektron E energiáját az

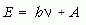
képlet határozza meg, amelyben A a kilépési munka, ez a képlet pedig számot ad arról a váratlan empirikus tényről, hogy a kilépő elektronok energiája nem a beeső fény intenzitásával, hanem frekvenciájával arányos.

Ezt az elképzelést azonban az elkövetkező húsz évben rajta kívül senki se fogadta el. Ha ugyanis a fény részecskékből állna, nem lehetne érteni az interferencia jelenségét. Einstein maga se tudta összeegyeztetni a fénykvantumokat az interferenciával, de azon az állásponton volt, hogy az energiamegmaradás a fontosabb, és majd ezen az alapon is sikerülni fog az interferenciát megérteni. Ebben igaza is lett, mert a kvantum-elektrodinamikában megszűnik az ellentét a fényenergia kvantáltsága és a fény interferenciaképessége között.

De a kvantum-elektrodinamikára még negyed századot kellett várni. Közben megszületett az atom Bohr-modellje, amely szerint az atom kvantumokban bocsátja ki vagy nyeli el a fényt, miközben egyik kvantumállapotból a másikba ugrik át. Ez tökéletesen összefér Einstein elgondolásával, hogy a fény is kvantumokból áll, de akkor ezt senki, még maga Bohr sem tartotta elképzelhetőnek.

A Bohr-modellt azonban valahogy mégis össze kellett egyeztetni az elektromágneses sugárzás elméletével (Maxwell elektrodinamikájával), és - mivel a fénykvantumokat sehogy se akarták elfogadni, - Bohr, Kramers és Slater (a kvantumelmélet hőskorának három nagy alakja) 1924-ben arra a következtetésre kényszerült, hogy az energiamegmaradás (az impulzus és a perdület megmaradásával együtt) csak átlagban teljesül, az egyedi atomi folyamatokban nem.

Ezt az elképzelést azonban már néhány hónap múlva megcáfolták, mert sikerült kísérletileg meggyőzően kimutatni, hogy az energia és az impulzus mindenegyes elemi atomi folyamatban külön megmarad - az ilyen típusú megfigyelések azóta is az energiamegmaradás egyre pontosabb bizonyítékául szolgálnak.

A béta-bomlás spektruma

A múlt század húszas éveiben már jól tudták, hogy a béta-bomlásban a bomló atom elektronkibocsátással alakul át. Úgy gondolták, hogy például a 210-es bizmut- izotóp (régi nevén rádium-E) bomlását a következő képlet fejezi ki:

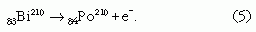
Az E = mc² képlet alapján a felszabaduló energia (m_Bi-m_Po-m_e)c²-tel egyenlő. Ez az impulzusmegmaradásnak megfelelően megoszlik a két bomlástermék között, de - mivel m_Po >> m_e - gyakorlatilag az elektron energiájával egyenlő.

A kilépő elektronnak tehát meghatározott energiával kellene rendelkeznie, de a tapasztalat szerint az energiája bizonyos valószínűséggel minden lehetséges értéket felvesz a nulla és a (m_Bi-m_Po-m_e)c² között (vagyis a spektrum ebben az intervallumban folytonos).

A béta-bomlás elmélete abban az időben még nem létezett, és sokan gondolták azt, hogy ebben a folyamatban az energiamegmaradás tétele nem teljesül és az energia egy része elvész. Ebbe azonban nem mindenki törődött bele. 1930-ban W. Pauli azzal a hipotézissel állt elő, hogy az energia a béta-bomlásban is megmarad, és a látszólag hiányzó energiát egy még ismeretlenrészecske, a neutrínó viszi el, amelyet nagyon nehéz észrevenni, mert elektromosan semleges.⁷ A bomlás helyes képlete tehát (5) helyett a következő:

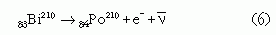
Néhány évvel később E. Fermi ennek a feltevésnek az Alapján részletesen kidolgozta a béta-bomlás (mai nevén gyenge kölcsönhatás) elméletét, amely egyebek között az elektronspektrum pontos alakját is megmagyarázza. Az elemi részek ma elfogadott klasszifikációja szerint az elektront kísérő részecskét a neutrínó antirészecskéjének tekintik és antineutrínónak hívják, ezért jelöltük ν helyett

A 20. század első harmadának ezek az eseményei végképp meggyőzték a fizikusokat arról, hogy az energiamegmaradást tapasztalatilag nagyon jól megalapozott természeti törvénynek tartsák. De ugyanebben a periódusban tisztán elméleti oldalról is fontos áttörés történt: E. Noether 1917-ben bebizonyította, hogy egy tetszőleges fizikai rendszer paramétereiből mindig képezhető egy olyan mennyiség, amely megmarad, ha a rendszert érő külső hatások időben változatlanok, és az ismert esetekben ez a mennyiség a rendszer energiájával egyenlő.⁸ Egy zárt (izolált) rendszer energiája tehát mindig megmarad, mert ez a rendszer a zártság fogalmából következően időben változatlan körülmények között van.⁹

Ezzel befejeztük azoknak az érveknek a vázlatos ismertetését, amelyek alapján a fizikusok az energiamegmaradás tételét különlegesen jól megalapozottnak tekintik. A fizika újkori története arra tanít, hogy az ilyen jól megalapozott fizikai törvényekről nem szokott kiderülni, hogy mégis tévesek. De az rendszeresen bekövetkezik, hogy ha kilépünk a jelenségeknek abból a köréből, amelyben a tételt igaznak találtuk, számíthatunk rá, hogy módosításra szorul. Mint láttuk, az energiamegmaradás tétele túlélt legalább három ilyenkritikus periódust: azt, amelyben a klasszikus mechanikáról a termodinamikára, majd pedig a kvantumfizikára és a részecskefizikára terjesztették ki. Mindhárom esetben diadalmasan került ki a megpróbáltatásokból. De kozmológiai méretekben - úgy látszik megkérdőjelezhető az érvényessége.

Ezt a következtetést a kozmológiai vöröseltolódásból lehet levonni, amely annak következménye, hogy minél hosszabb ideig utazik hozzánk a fénysugár (minél távolabbi galaxisból jön), annál nagyobbra nő a hullámhossza (annál inkább eltolódik a színe a vörös felé). Ha figyelembe vesszük, hogy a fény fotonokból áll, amelyeknek az energiáját az E = hν = hc/λ képlet határozza meg,¹⁰ akkor nyilvánvaló, hogy a fénysugár energiája a terjedés közben fokozatosan csökken.

Az általános relativitáselmélet egyértelmű magyarázatot ad erre a jelenségre: az energiacsökkenés (hullámhossz- növekedés) oka a Világegyetem tágulása (2. ábra). Matematika nélkül ezt így lehet szemléltetni: ha a geometriai teret háromdimenziós helyett kétdimenziósnak tekintjük, akkor a táguló Világegyetemet egy felfúvódó léggömbhöz hasonlíthatjuk.¹¹ A léggömbre rajzolt pontok a galaxisok, közülük az egyik a mi Tejútunk, amelyben kétdimenziós laposlényekként éldegélünk. A többi galaxisról a fénysugár a gömb felületén haladva¹² érkezik el hozzánk, és ahogy a gömb lassan felfúvódik, a sugarával arányosan nő a hullámhossza. Ugyanilyen arányban távolodnak a galaxisok is egymástól.

Ez a jelenség teljesen összefér a Noether-tétellel: a fény nyilvánvalóan idoben változó körülmények között terjed, és ezért nem is kell, hogy az energiája megmaradjon. A tér-léggömb analógia alapján logikus arra gondolni, hogy a felfúvódásnál magának a geometriai térnek (a léggömbnek) az energiája is változhat és esetleg pont annyival nő, amennyi a fénysugár energiájából elvész. De gondoljuk meg jobban, tényleg indokolt-e ez a várakozás. A Noether-tételből következik, hogy egy zárt (izolált) rendszer energiája megmarad, mert - mint mondottuk - ez a rendszer a zártság fogalmából következően időben változatlan külső körülmények között van. De a Világegyetemnek, mint egésznek, nyilván nincsenek "külső körülményei", a Noether-tételnek ez a következménye tehát aligha alkalmazható rá. Ezért arra a kérdésre, hogy a fénysugárban és a geometriai tér görbületében tárolt teljes energia valóban megmarad-e, csak az általános relativitáselmélet konkrét egyenleteinek alapján lehet válaszolni. Az derül ki, hogy a geometriai teret (pontosabban téridőt) jellemző paraméterekből valóban képezhető egy olyan mennyiség, amely nagyon emlékeztet az energiára, és nagysága éppen annyival nő, amennyi energiát a fénysugár elveszít. Azonban ennek a mennyiségnek a tulajdonságai nem minden szempontból olyanok, mint amit az energiától elvárhatunk, ezért nem is energiának, hanem pszeudoenergiának hívják. Indokolt tehát az az óvatos megfogalmazás, hogy valóban kozmikus méretekben az energiamegmaradás érvényessége megkérdőjelezhető.

De baj ez? Csak akkor okozna gondot, ha ez a körülmény kétségessé tenné, amit az energiamegmaradásról korábban megállapítottunk, hogy ez a legjobban megalapozott természeti törvények egyike. Erről azonban szó sincs. Tegyük fel ugyanis, hogy földi viszonyok között az energiamegmaradás ugyanolyan mértékben sérül, mint a kozmológiai vöröseltolódásban. Ebben a jelenségben a hullámhossz időegységre jutó relatív csökkenését a Hubble-konstans határozza meg, amelynek hozzávetőleges tapasztalati értéke H ≈ 10^-10 év-¹-nel egyenlő,¹³ vagyis a kozmológiai vöröseltolódásban a hullámhossz egy év alatt körülbelül 10 milliárdod részével csökken. Ilyen arányban sérülhetne az energiamegmaradás törvénye, ha mértéke a kozmológiai vöröseltolódásnak felelne meg. Ez rendkívül kismértékű sérülés, de az elméleti megfontolások abba az irányba mutatnak, hogy a Világegyetem tágulása a lokális jelenségeket még ennyire se befolyásolja, sőt az is lehet, hogy egyáltalán nincs rájuk hatással

Az érvelésünk végére értünk, a címben feltett kérdésre válaszoltunk. Azt találtuk, hogy az energiamegmaradás törvénye se empirikus, se induktív értelemben sem tekinthető bizonyosnak, de rendkívül jól megalapozott törvény, amelynek plauzibilitását az 1-hez nagyon közeli értékkel fejezhetjük ki. De azért marad egy praktikus probléma. Mit válaszoljunk annak, aki felteszi nekünk a címbeli kérdést, azonban nincs módunk arra, hogy olyan viszonylag részletes választ adjunk rá, mint ebben a cikkben. Ez gyakran megtörténhet a legkülönbözőbb okokból: nincs elég időnk, a kérdezőt nem érdekli a kérdés annyira, hogy türelmesen végighallgasson egy hosszú fejtegetést, vagy ehhez nincsenek még meg a szükséges előismeretei. Ez utóbbi vonatkozik a középiskolára, még abban az esetben is, amikor a kérdést egy kifejezetten érdeklődő tanuló teszi fel a tanárának. Szerintem ilyen szituációban, amikor csak rövid választ adhatunk, amely elkerülhetetlenül leegyszerűsítő, azt kell válaszolnunk, hogy igen, az energia biztosan megmarad. Ezzel csak egészen minimális mértékben vezetjük félre a kérdezőt, míg ha azt válaszolnánk, hogy az energia nem marad meg biztosan, tökéletesen helytelen irányba indíthatnánk el a gondolkodását. A cél azonban tagadhatatlanul az, hogy már az iskolában olyan felfogásban tanítsuk az energiamegmaradást, amely a lehető legjobban megfelel a plauzibilitáson alapuló történeti értékelésnek. A képletekkel való számolás gyakorlása az általános oktatásban csak akkor indokolt, ha ennek a célnak a szolgálatában áll.

_______________________________