Fizikai Szemle honlap |
Tartalomjegyzék |
Vannay László, Fülöp Ferenc, Máthé József, Nagy Tamás
BME, Fizikai Intézet, Kísérleti Fizika Tanszék
A fizika Országos Középiskolai Tanulmányi Verseny - a 2007/2008-as tanévtől kezdődően - két csoportban (kategóriában) kerül megrendezésre. A diákok hovatartozása a versenykiírás szerint: "Az I. kategóriába azok a középiskolai tanulók, akik nem tartoznak a II. kategóriába. A II. kategóriába azok a gimnáziumi tanulók, akik a 9. évfolyamtól kezdődően - az egyes tanévek heti óraszámát összeadva - a versenyben való részvétel tanévének heti óraszámával bezárólag összesen heti 8, vagy annál több órában tanulják a fizikát bizonyítványban feltüntetett tantárgyként."
Mind a két csoport részére három fordulóból áll a verseny. Az első két forduló során elméleti problémákat kell megoldaniuk a versenyzőknek, míg a harmadik fordulóban mérési feladatokkal kell megbirkózniuk. A harmadik fordulóban az első két forduló legjobbjai mérik össze tudásukat.
A verseny értékelése a második (a II. kategóriánál maximum 60 pont) és a harmadik (a II. kategóriánál maximum 40 pont) fordulóban szerzett pontok összegzésével történik.
A BME Fizikai Intézet a II. kategória versenyének harmadik - döntő - fordulóját rendezte. A versenyen 30 diák vett részt, két 15 fős csoportban. Az egyik csoport délelőtt, 8-tól 12 óráig, a másik 13-tól 17 óráig dolgozhatott, egymástól függönnyel elválasztott mérőhelyeken. A mérőhelyeket kisorsoltuk a versenyzők között.
Cikkünkben először bemutatjuk a verseny kezdetekor kiadott írásos anyagot, utána vázoljuk a kitűzött feladatok megoldásának módját, majd beszámolunk az értékelés során szerzett tapasztalatokról, a versenyzők eredményeiről, és végül köszönetet mondunk mindazoknak, akik közreműködtek a verseny előkészítésében vagy lebonyolításában
A feladat megoldásához rendelkezésre álló eszközök
További információk
A verseny időtartama 4 óra.
Az elkészített jegyzőkönyve minden lapján, az első oldal jobb felső sarkában tüntesse fel a mérőhely számát, valamint azt, hogy a délelőtti (De.), vagy a délutáni (Du.) csoportban mért. Egyéb azonosításra alkalmas adatot (név, iskola stb.) ne tüntessen fel!
Ha a kiadott eszközök kezelésével kapcsolatban problémái vannak, vagy az eszközök működésénél rendellenességet tapasztal, forduljon a felügyelő tanárokhoz.
A méréseket körültekintően végezze.
A tápegységeket csak az áramkör összeállítása és gondos ellenőrzése után csatlakoztassa a vizsgált kapcsolásra.
Tartsa be az általános balesetvédelmi szabályokat.
Vigyázzon saját maga és a kiadott eszközök épségére.
Eredményes versenyzést kívánunk.
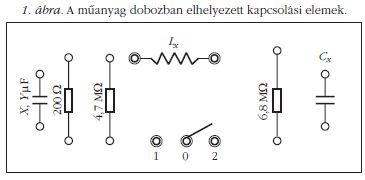
Megjegyzés: ha a műanyag dobozt a benne lévő kapcsoló irányából nézzük, az "ismert" kondenzátor a bal szélen helyezkedett el, kapacitásának értékét - amely mérőhelyenként eltért - a vázlaton megadtuk.
Kapacitásmérés rezonanciamódszerrel
Ha sorba kapcsolunk R ohmos ellenállást, C kapacitású kondenzátort és L önindukciós együtthatójú tekercset, soros rezgőkört kapunk. Ha a soros rezgőkörre, f frekvenciájú, ω = 2 π f körfrekvenciájú szinuszos feszültséget kapcsolunk, az elemeken átfolyó I áramértéke:
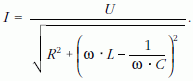
Az áram láthatóan a frekvencia függvénye. Maximális értékét az f0 rezonanciafrekvenciánál veszi fel, amikor:
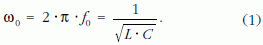
Abban az esetben, ha a tekercset és a kondenzátort párhuzamosan kapcsoljuk, párhuzamos rezgőkört kapunk, melynél a frekvencia változtatásával, rezonanciafrekvenciánál áramminimumot tapasztalunk. A párhuzamos rezgőkörnél is az (1) egyenlet adja meg a rezonanciafrekvencia és a kapcsolási elemek jellemzői közötti kapcsolatot.
Megállapíthatjuk, hogy a rezonanciamódszerek egyaránt alkalmasak kapacitás, és önindukciós együttható mérésére. Ha kapacitást (Cx ) szeretnénk mérni a rezgőkör összeállítása után (2. ábra), a feszültségforrás frekvenciájának változtatásával megkeressük az fx rezonanciafrekvenciát, és ha ismerjük az alkalmazott tekercs L önindukciós együtthatóját, az (1) összefüggés felhasználásával meghatározhatjuk a keresett kapacitás értékét.
Ha, mint esetünkben, nem ismerjük a tekercs önindukciós együtthatóját, egy ismert C0 kapacitású kondenzátor segítségével, rezonanciamódszerrel megmérhetjük az ismeretlent. A rezonanciafrekvenciát ebben az esetben jelöljük f0-val.
A feladat megoldható a rendelkezésre álló tekercs önindukciós együtthatójának meghatározása nélkül is, hiszen az ismert és az ismeretlen kapacitású kondenzátorokkal mért rezonanciafrekvenciákkal a kapacitások aránya:
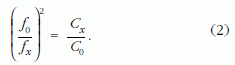
Az ismert kapacitások értéke mérőhelyenként 4,57 és 4,72 µF között változott. A tekercsek önindukciós együtthatója, pedig 1,26 és 1,59 H közötti értéket vett fel. A hanggenerátor frekvenciáját 0,1 Hz-enként lehetett változtatni, így a rezonanciafrekvencia a rezonanciagörbe felvétele nélkül is jól meghatározható volt.
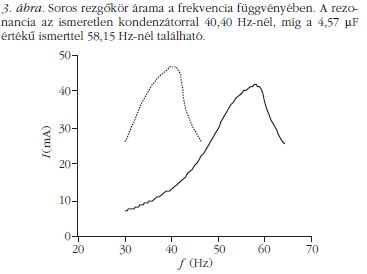
Egy soros rezgőkör ismert és ismeretlen kondenzátorral mért rezonanciagörbéjét mutatja a 3. ábra. Az ismert 4,57 µF kapacitású kondenzátorral 58,15 Hz-nél, míg az ismeretlen kondenzátorral 40,40 Hznél található a rezonanciafrekvencia, így a (2) egyenlet felhasználásával a keresett Cx kapacitás értéke 9,47 µF.
A feladat kiírásakor arra gondoltunk, hogy ha adott U1 feszültségre feltöltött ismeretlen Cx kapacitású kondenzátort összekapcsolunk egy ismert, kisütött C2 kapacitással, a kialakuló közös U2 feszültséget megmérve, a töltésmegmaradás elvét figyelembe véve, meghatározható a keresett kapacitás. A vonatkozó összefüggés:
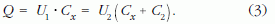
Ennél a megoldásnál a feszültséget mérő műszer belső ellenállásán keresztül történő kisülés miatt problematikus az összekapcsolás pillanatában kialakuló közös feszültség értékének meghatározása. A két összekapcsolt kondenzátor feszültségmérő műszeren keresztül történő kisülési folyamatának vizsgálata ad lehetőséget ennek a feszültségnek a meghatározására.
Ha egy feltöltött kondenzátor ellenálláson keresztül sül ki, a feszültség időbeli változása az alábbi összefüggés szerint alakul:
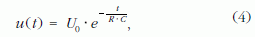
ahol C a kondenzátor kapacitása, R az ellenállás értéke, t az idő, és U0 a t = 0 időponthoz tartozó feszültség.
A (4) kifejezés - voltban kifejezett értékének - természetes alapú logaritmusa egy egyenes egyenletét adja:
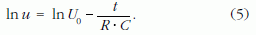
Az egyenes t = 0 ponthoz tartozó tengelymetszete a kiinduló feszültség logaritmusa.
Az elmondottaknak megfelelően a vizsgált kapacitást 10 V-ra feltöltöttük, majd összekapcsoltuk az ismert kapacitású kondenzátorral és felvettük a feszültség- idő függvényt. A mért feszültségértékek logaritmusát ábrázolva az idő függvényében a mérési pontokra egyenest illesztettünk (4. ábra). A mérési pontok igen jól illeszkedtek a felvett egyenesre.
 |
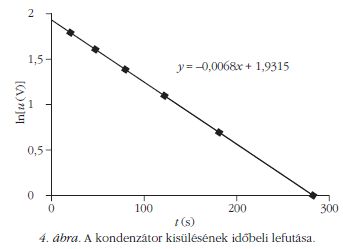 |
Az egyenes egyenletéből lnU0 = 1,9315 és ebból U0 értéke 6,8998, azaz 6,9 V.
A (3) egyenletből:
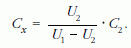
C2 = µF értékkel számolva Cx = 10,17 µF.
Az általunk várt, és fent leírt módszert csak néhányan alkalmazták. Legtöbben azt a megoldást választották, hogy az ismert és az ismeretlen kondenzátort sorba kötve kapcsolták egy egyenfeszültségű tápegységre, és a kondenzátorokon mért feszültségek összehasonlításával oldották meg a feladatot.
Többen választották azt a megoldást, hogy a kondenzátorokat sorba, vagy párhuzamosan kapcsolva, áram- és feszültségméréssel, Ohm-törvény alapján impedanciát mértek.
Természetesen minden jó megoldást elfogadtunk.
Mint korábban leírtuk, a feltöltött kondenzátor ellenálláson keresztül történő kisülésekor a kondenzátor feszültsége a (4) összefüggés szerint változik. A kondenzátor feszültségének természetes alapú logaritmusa az (5) egyenlet szerint egy egyenes egyenletét adja. Tehát a mérési pontokra egyenest illesztve, annak meredeksége: -1 / (R · C).
Az elmondottak alapján, ha a vizsgált Cx kapacitású kondenzátort U0 feszültségre feltöltjük, majd a feszültségmérő Rx belső ellenállásán keresztül kisütjük, a feszültség logaritmusának idő függvényeként kapott egyenes meredeksége:
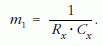
Abban az esetben, ha az előbbi mérést megismételjük, de a kondenzátort a feszültségmérővel párhuzamosan kötött, ismert R0 ellenálláson keresztül sütjük ki, a mérőpontokra illesztett egyenes meredeksége:
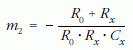
lesz. A két meredekségre kapott kifejezésből meghatározható a vizsgált kapacitás és a feszültségmérő belső ellenállásának értéke:
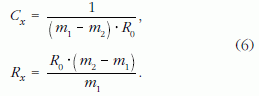
Az ismeretlen kapacitású feltöltött kondenzátort a feszültségmérő belső ellenállásán kisütve mértük a kondenzátor feszültségét az idő függvényében. Az eredményeket felhasználva kaptuk az 5. ábra a egyenesét.
A b egyeneshez tartozó mérési pontoknak megfelelő feszültségértékeket akkor kaptuk, amikor a feltöltött kondenzátort a feszültségmérővel párhuzamosan kapcsolt 11,5 M&Omega-os ellenálláson keresztül sütöttük ki.
A (6) összefüggésekből, a mérési pontokra illesztett egyenesek egyenletéből kapott meredekségek felhasználásával Cx = 9,99 µF és Rx = 10,11 MΩ. (A voltmérő gépkönyve 10 MΩ-nak adta meg a műszer belső ellenállását.)
A kisütés előtt a kondenzátort 10 V-ra töltöttük fel (ln10 = 2,3025), a mérési pontokra illesztett egyenesek 10,04, illetve 10,08 V-nál metszik az y tengelyt. A kisütés kezdetén, amikor a feszültség gyorsabban változik, a rövid idők mérési pontossága kisebb, mint a hosszabb időké. Javíthattunk volna az eljárás pontosságán, ha nem vesszük figyelembe a mért rövidebb időket.
A leírt eljárásnál gyorsabban lehet a feladatot megoldani, ha csak egy olyan időpontot vizsgálunk, amikor a kisülő kondenzátor feszültsége a kiindulási érték adott hányadát éri el, például a felét, vagy e -ed részét. A legegyszerűbb az utóbbi eset.
Jelöljük t1-gyel és t2-vel azt az időt, amely idő alatt a kiindulási feszültség az e -ed részét éri el a feszültségmérőn, illetve a feszültségmérőn és a vele párhuzamosan kapcsolt ellenálláson keresztül kisütve. A (4) egyenletből (a korábbi jelöléseket alkalmazva):
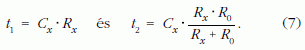
A fenti két egyenletből a két ismeretlen meghatározható.
A feladat 2. pontjában a voltmérő belső ellenállásának meghatározását kértük. Ez valójában nem jelentett újabb mérési feladatot, hiszen a kisülési folyamat vizsgálatával megválaszolható a kérdés.
Megjegyezzük, hogy nagy ellenállások mérésére szokták alkalmazni a módszert.
Azzal a megfogalmazással, hogy "mérési adatai felhasználásával határozza meg a feladat megoldásakor feszültségmérésre használandó műszer belső ellenállását", arra utaltunk, hogy nem kell külön méréseket végezni a belső ellenállás meghatározásához. Ahogy azt leírtuk, a kisütési folyamat vizsgálatánál kapott adatokból ez a kérdés is megválaszolható. A műszer belső ellenállását a várt módon csak egy-két versenyző határozta meg.
Néhányan úgy határozták meg a belső ellenállást, hogy adott egyenfeszültségre egy nagy értékű, ismert R0 ellenállással sorba kötve a voltmérőt, mérték a műszerre eső feszültséget. A tápegység U0 feszültségének és a voltmérő UV feszültségének különbsége az ismert ellenálláson eső UR feszültség. A körben folyó áramra felírt egyenletből a műszer Rb belső ellenállása meghatározható:
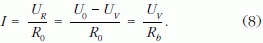
A voltmérő belső ellenállásának nagyságrendjébe eső, nagy értékű ellenállás mellett a tápegység belső ellenállása elhanyagolható, a módszer alkalmazható.
A feladat összeállításakor úgy gondoltuk, hogy a rezonanciamódszerek valamelyikét - valószínűleg a soros rezgőkört - mindegyik versenyző alkalmazni fogja. Meglepetéssel tapasztaltuk, hogy a versenyzőknek majdnem fele egyik módszert sem alkalmazta. Tehát a feladatnak ezt a részét nem oldották meg.
Mint azt a Kapacitásmérés egy ismert és az ismeretlen kapacitás összekapcsolásával pontban leírtuk, a feltöltött és a feltöltetlen kondenzátor összekapcsolásával, az így kialakuló közös feszültség meghatározásával, majd a (3) összefüggés alkalmazásával csak néhányan (7 fő) oldották meg a feladatot. Közülük többen megemlítették a közös feszültség mérésénél tapasztalt nagy bizonytalanságot, amelynek csökkentésére a "gyorsan kell mérni" megoldást javasolták.
16 versenyző próbálta más módszerrel megoldani a feladatot, az általuk alkalmazott módszerekre már korábban utaltunk.
A kisülési folyamat vizsgálatával a versenyzőknek több mint a fele foglalkozott. Néhányan idő hiányában csak írtak a módszerről. 15-en méréseket is végeztek, és a mérési eredmények feldolgozásával is foglalkoztak. Sajnos közülük sokan megfeledkeztek a feszültségmérő belső ellenállásáról. Négyen oldották meg lényegében jól a feladatnak ezt a részét, közülük egy versenyző megoldása volt teljes értékű.
A versenyzők munkájának értékelésénél szembetűnő volt, a korábbi versenyekhez viszonyítva:
A második és a harmadik fordulón elért pontszámok összesítése után az élmezőnyben a sorrend az alábbiak szerint alakult:
5.Lovas Lia Izabella (Pécs, Leőwey Klára Gimn.), 6. Karsa Anita (Budapest, Fazekas Mihály Főv. Gyak. Ált. Isk. és Gimn.), 7. Aczél Gergely (Pápa, Pápai Református Kollégium Gimnáziuma), 8. Földes Imre (Szolnok, Verseghy Ferenc Gimn.), 9. Mayer Jakab Balázs (Szeged, SZTE Ságvári Endre Gyak. Gimn.), 10. Almády Balázs (Tata, Eötvös József Gimn. és Koll.), 11. Pálovics Péter (Zalaegerszeg, Zrínyi Miklós Gimn.), 12. Trényi Róbert (Szeged, Radnóti Miklós Gyak. Gimn.), 13. Lászlóffy András (Budapest, Piarista Gimn.), 14. Szabó Dávid (Budapest, Fazekas Mihály Főv. Gyak. Ált. Isk. és Gimn.), 15. Horváth Dávid (Miskolc, Herman Ottó Gimn.).
A verseny lebonyolításához szükséges anyagi hátteret részben az Oktatási Hivatal biztosította. Ezt ezúton is köszönjük.
A verseny lebonyolításához szükséges eszközök kivitelezéséért Horváth Bélának és Halász Tibornak, a megfelelő körülmények megteremtéséért Gál Bélánénak és Mezey Miklósnak jár a köszönet. A feladat kitűzésével, a verseny lebonyolításával kapcsolatos hasznos tanácsaiért Kálmán Péternek és Keszthelyi Tamásnak mondunk köszönetet.
A versennyel kapcsolatos adminisztrációs és gazdasági ügyek intézéséért Köves Endrénét és Gál Bélánét illeti köszönet.
Elismerés és köszönet illeti mindazokat, (szülőket, tanárokat, barátokat stb.) akik segítették a versenyzők munkáját és ezzel hozzájárultak a verseny sikeréhez.