Fizikai Szemle honlap |
Tartalomjegyzék |
Holics László, Apáczai Csere János Gyakorló Gimnázium
Sükösd Csaba, BME Nukleáris Technika Tanszék
Szakmai és esztétikai élményekben gazdag egyhetes továbbképzésben vehettem részt (Holics László) 2009 augusztusában, amikor csatlakoztam a magyar fizikatanárok csoportja számára a CERN-be szervezett tanulmányúthoz. A szakmai részt az előadások és "műhelylátogatások" jelentették, amelyek során a Világegyetem keletkezésének, fejlődésének titkait ostromló elméletekről hallottunk és az intézet berendezéseit látogattuk meg. Az esztétikai részt egy záró hangverseny meghallgatásának élménye, valamint a Mont Blanc 3842 m magas kilátójának meglátogatása jelentette. Innen széttekintve a természet hideg és megkapó csodáját élvezhettük és zárhattuk magunkba egy életre szólóan.
Az utat azonban magunknak is aktívan kellett végigjárni, ugyanis nemcsak a műhelyfoglalkozásokon volt tevőleges szerepünk (pl. egy Wilson-kamra építésével), hanem az általunk tervezett kísérleteket is el kellett végezni, kollégáinknak bemutatni. Ilyen feladat volt például a Torricelli-kísérlet elvégzése vízzel a CERN szintjén és a hegytetőn, a radonkoncentráció mérése, a vízforráspontjának meghatározása különböző nyomásokon. A mérőkísérletek ösztönzője, javaslója Sükösd Csaba volt, az utazás szervezője, aki itthonról kísérte figyelemmel az eseményeket. Számomra egy különös kísérlet elvégzését javasolta. Maga az eljárás rendkívül egyszerű, minden iskolában elvégzik, azonban most azt a célt tűzte ki számunkra, hogy végezzük el a hangsebesség hőmérséklettől való függése elméleti törvényének kísérleti ellenőrzését. A hang terjedési sebessége az elmélet szerint ugyanis az abszolút hőmérséklet négyzetgyökével arányos (függetlenül a nyomástól).
A méréseket előre kialakított csoportokban kellett elvégezni. Az én csoportomba hivatalosan csak ifj. Holics László tartozott, ám időközben többen odasereglettek, és közreműködtek a mérés elvégzésében, az adatok leolvasásában.
A hangsebesség-mérési kísérletre a következőket készítettem elő:
Megvizsgálni, hogy a levegőben két különböző hőmérsékleten mért hangterjedés sebességének aránya követi-e az abszolút hőmérsékletek arányának négyzetgyökét. Ezért ezt a mérést a CERN területén, a legmelegebb időszakban, és a Mont Blanc-ra tett kirándulásunk leghidegebb helyén végeztük el a legegyszerűbb, levegőoszlop-rezonanciás módszerrel. Mindegyik méréssorozatban két, különböző frekvenciájú hangvillát használtunk, a nagyobb frekvenciával keltett rezgések esetén a negyed- és háromnegyed hullámhosszú eseteket is megvizsgáltuk, majd a három méréssorozat átlagát fogadtuk el helyes értéknek.
Mikroszkopikus, molekuláris modell
A hang terjedési sebessége levegőben független a nyomástól és a sűrűségtől, csak a hőmérséklet függvénye.
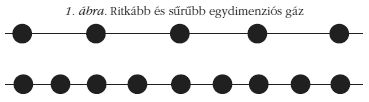
Első pillanatban meglepő ez a megállapítás, hiszen a hang tulajdonképpen valamilyen (többé-kevésbé periodikusan változó) zavar, és így a terjedését gázokban a molekulák egymással történő ütközéseinek kell közvetíteni. Ezért úgy gondolhatnánk, hogy sűrűbb gázban gyakrabban ütköznek a molekulák, és emiatt a zavarnak is gyorsabban kell terjednie. Nagyon egyszerű belátni azonban, hogy ez nincs így. Tekintsük az 1. ábrán látható egyszerű, "egydimenziós" gáz modellt. Az ábra felső részén a "gáz" sűrűsége fele akkora, mint az alsó részen. Ha fent a molekulák középpontjainak átlagos távolsága d, akkor lent d/2. (A rajz természetesen torzít abban a tekintetben, hogy a molekulák sugara általában elhanyagolható a molekulák közötti távolsághoz képest, azaz a molekulák pontszerűnek tekinthetők.)
Először tegyük fel, hogy a molekulák "állnak". Hozzunk létre egy "zavart", és lökjük meg a bal szélső molekulát v sebességgel! Vizsgáljuk meg, mikorra érkezik ez a zavar a lánc végére! Tegyük fel azt is, hogy a molekulák ütközése tökéletesen rugalmas! Az ábra felső részében ábrázolt "gázban" az első ütközésig eltelt idő t = d/v. Mivel egydimenziós esetben csak egyenes ütközés lehetséges (és mivel a molekulák tömege azonos), ezért a második molekula is v sebességgel folytatja az utat az ütközés után (mint két biliárdgolyó egyenes ütközése). Tehát újabb t d/v idő múlva ütközik a következővel stb. Ha a lánc hossza L = Nd, akkor a "zavar" a lánc végére
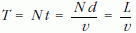
idő múlva érkezik meg. Ugyanezt az időt kapjuk azonban az ábrán lévő "alsó" lánc esetén is, pedig ott a gáz sűrűsége kétszer akkora. Két ütközés között persze feleakkora idő telik el, mint a fenti esetben, azaz
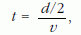
viszont a zavarnak az L távolság megtételéhez kétszer annyi ütközésre van szüksége! Azaz a zavar terjedési sebessége valóban független a gázsűrűségétől, csak a molekulák sebességétől függ! A zavar terjedési sebessége a fentiek alapján ebben a modellben:
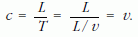
A fenti egyszerű modellben a molekulák álltak, és csak a "zavar" következtében volt sebességük. A valódi gázokban azonban a molekulák mozognak, és átlagos sebességüket a hőmérséklet határozza meg az ekvipartíció tételének megfelelően. Például egy egydimenziós ideális gázban, ahol csak egy szabadsági fok van:
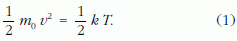
A hang által létrehozott "sebességzavar" általában a hőmozgás sebességéhez képest elhanyagolható perturbációt jelent. Emiatt jó közelítéssel mondhatjuk, hogy a zavar terjedését a molekulák hőmozgásának sebessége határozza meg, hiszen a molekulák ezzel a sebességgel tudják egymásnak átadni a perturbációt.
Az (1) képletből azonnal látszik, hogy
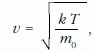
azaz a molekulák sebessége - és így a hang terjedési sebessége is - a hőmérséklet négyzetgyökös függvénye.
Ha a gázok ténylegesen egydimenziósak lennének - mint a modellünkben - akkor ez a képlet tökéletesen érvényes lenne, hiszen akkor ütközéskor az energiacsere csak egyetlen szabadsági fokra szorítkozna. A valódi gázoknak azonban több szabadsági foka van. Még az atomos gázoknak is három (a térbeli háromdimenziós mozgás következtében), a kétatomos molekuláknak pedig öt (mert még foroghatnak is két, egymásra merőleges tengely körül). Egy ütközéskor tehát a zavart jelentő energiatöbblet több szabadsági fokra oszlik szét, emiatt a zavar terjedése valamivel lassabb lesz, mint a molekulák sebessége. Ez a (molekuláris) magyarázata annak, hogy a fenti képletbe még bekerül egy, a molekulák szabadsági fokainak számától függő tényező is.
Pontos - itt nem részletezendő - számítások szerint a hang terjedési sebessége a következőképpen függ a molekulák szabadsági fokainak f számától:
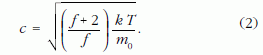
A valódi gázokban a molekulák háromdimenziós térben mozognak, és így az átlagos transzlációs sebességük
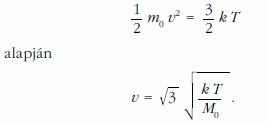
A hangsebesség és a molekuláris sebesség kapcsolata tehát:
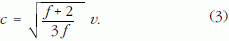
Mivel a levegő kétatomos molekulák keveréke, így f =5, ezért
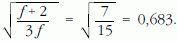
Azaz a hang terjedési sebessége a gázmolekulák sebességének körülbelül 68%-a. Ez a következménye annak, hogy az ütközéskor a zavart jelentő energia több szabadsági fokra is szétosztódik.
Makroszkopikus leírás
A hullám terjedési sebessége (ideális) gázokban
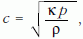
ahol κ a fajhőviszony. Könnyű belátni itt is, hogy a p nyomás és ρ sűrűség kiesik. Felhasználva ugyanis az általános gáztörvényt, a nyomás kifejezhető:
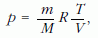
és a sűrűség
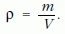
Ezeket beírva a hangterjedés sebességének kifejezésébe a következőt kapjuk:
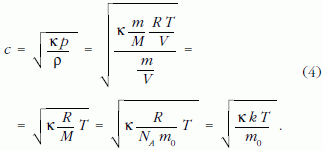
ahol κ = cp /cv és k = R/NA a Boltzmann-állandó, NA az Avogadro-állandó, m0 pedig egyetlen molekula tömege. (Ismeretes, hogy κ = cp /cv = (f +2)/f, ahol f a gázmolekulák szabadsági fokainak száma, így ez az öszszefüggés összhangban van a (2) formulával.)

Látható, hogy az abszolút hőmérsékleten kívül minden állandó, tehát a hangsebesség csak a hőmérséklettől függ. Megjegyezzük azonban, hogy ez az összefüggés homogén összetételű gázban (vagy keverékben) érvényes, vagyis az m0 részecsketömeg valójában egy átlagos értéket jelent. Ez a tény bizonyos hibát okozhat, amennyiben a két mérés (a meleg és a hideg levegőben történő hangsebességmérés) hőmérséklet-különbségét úgy értük el, hogy a forró levegőt Genf tengerszint feletti 375 m magasságában "szereztük be", ahol 38,5 °C volt a hőmérséklet, és a hideget úgy "állítottuk elő", hogy felmentünk a Mont Blanc (majdnem) tetejére, ahol 4,5 °C hőmérsékletet mértünk.

Meg kell jegyezni, hogy a két hely között mintegy 3500 m volt a magasságkülönbség, ami a levegő molekuláris összetételében (az összetevők arányában, tehát az átlagos m0 molekulatömegben) eltérést okozhat. Ennek hatását a barometrikus magasságformula alapján megbecsülhetjük. Az eredmény az, hogy az átlagos molekulatömeg megváltozása elhanyagolhatóan kicsi. Így tehát várható, hogy jó közelítéssel igaz: az általunk mért hangsebességek aránya az abszolút hőmérsékletek arányának négyzetgyökével egyenlő. Vagyis

Ezt kívántuk kísérlettel igazolni.
A témában tovább elmélyülni kívánók figyelmét felhívjuk a cikk végén található irodalomjegyzékre.
|
A mérés során egy plexicsőből készített talpas edénybe öntött vízoszlopból lassan kihúzott csőben keltettünk kényszerrezgést a megütött hangvillával. A kihúzott csövet alulról zárttá tette az edényben levő víz, felső vége pedig nyitott maradt, ahol a gerjesztést végeztük. |
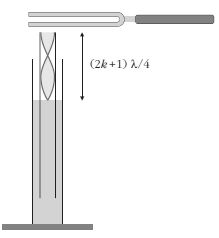
|
A hangvilla kényszerrezgésbe hozta a csőben levő levegőoszlopot, s miközben a plexicsövet lassan húztuk kifelé az edényből, a hallott hang ereje fokozatosan erősödött, majd halkult, a nagyobb frekvencia alkalmazása esetén újból erősödött. A maximális erősödés akkor lép fel, amikor az alulról vízzel zárt légoszlop csőben levő részének hossza a hanghullám hosszának negyedrészével, vagy annak páratlan számú többszörösével egyenlő. Rezonancia esetén a vízfelületről visszaverődő hullám és a beérkező hullám alkotta állóhullámnak nyomásmaximuma van a vízfelületnél keletkező csomópontban és sebességmaximuma a szabad végen kialakuló duzzadóhelyen. Ekkor maximális a hallott hang erőssége. Az ehhez tartozó negyed, illetve 3/4 hullámhosszat a kihúzható cső oldalára erősített acél mérőszalagról könnyen leolvashatjuk (az alábbi mérési jegyzőkönyvekben a leolvasott érték jele: L).

A leolvasás pontosságát két tényező befolyásolja.
Ennek magyarázata az általában a biológiai érzékelése vonatkozó Weber-Fechner-törvény. Eszerint mi egy inger relatív megváltozását érzékeljük: Δq = constΔI /I, ahol Δq az általunk érzékelt változás, és ΔI pedig az inger tényleges megváltozása. Emiatt I ~ 0 környékén kis intenzitásváltozást is könnyen érzékelünk (mert a nevező nagyon kicsi), viszont eléggé nehezen érzékelünk intenzitásváltozást, ha I nagy. AWeber-Fechner-törvény következménye az érzékeléseink logaritmikus jellege is, hiszen a fenti egyenletből kapjuk: dq/dI = const/I, és ezt integrálva adódik: q = log (I/I0). Itt I0 az érzékelési küszöb, az az intenzitás, amelyre adott válaszunk éppen 0 (azaz még éppen nem érzékeljük). Ez azok a például annak is, hogy a használt hangerősségi skála (decibelskála) logaritmikus.
 |
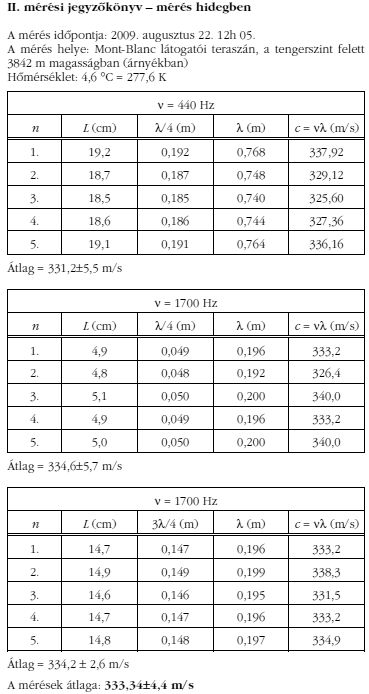 |
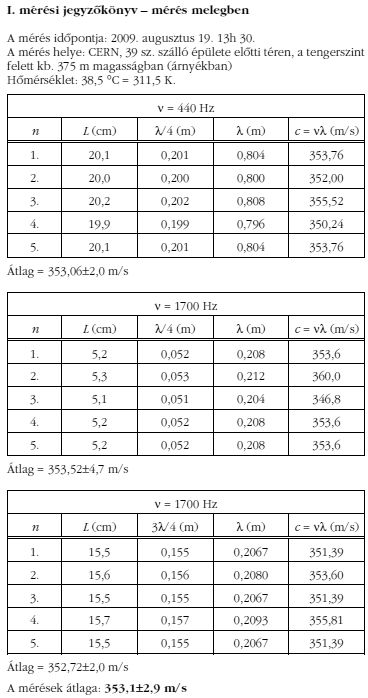
A mind a CERN-i kánikulai hőmérsékleten, mind a Mont Blanc-i hidegben elvégzett mérési eredmények átlagértékét és empirikus szórását a következő képletek alapján határoztuk meg:
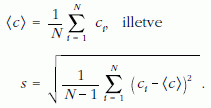
Megjegyzések
A mérések eredménye A két hangsebesség aránya (és hibája):
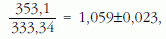
a hőmérsékletek arányának négyzetgyöke pedig:
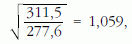
ami nagyon jó egyezés!
Az, hogy az egyezés ezrelékre pontos, teljesen a véletlen műve, hiszen - mint az empirikus szórások is mutatják - a méréseink hibája az ezreléknél jóval nagyobb. Azt viszont nyugodtan állíthatjuk, hogy a hangsebesség hőmérséklettől való függését a mérési hibán belül sikerült igazolnunk. (A méréseket id. Holics László és ifj. Holics László végezték.)
A kísérlet egyszerű, végrehajtása gyors, ezért iskolai órán is elvégezhető. Ha a két mérést egymástól időben "távol" végezzük - egyszer amikor jó idő és meleg van, egyszer pedig egy téli periódusban (ilyen időszakok mind az őszi, mind a tavaszi félévekben kiválaszthatók) -,akkor a hangsebesség hőmérséklettől való függését anélkül is igazolhatjuk az iskolában, hogy ehhez a Mont Blanc-ra kelljen felmenni. Megfelelő motivációval az első kísérlet elvégzése után a tanulók már várni fogják a második kísérlet végrehajtásához szükséges hőmérséklet-változást, és a második kísérlet végrehajtását.
Nagy Anett,Papp Katalin: Hangszerek a "semmiből". Fizikai Szemle 59/2 (2009) 64.
http://www.kfki.hu/fszemle/archivum/fsz0902/nagya0902.html#t2
http://hu.wikipedia.org/wiki/Hangsebesség (magyarul)
http://en.wikipedia.org/wiki/Speed_of_sound (angolul)