Fizikai Szemle honlap |
Tartalomjegyzék |
Bigus Imre
Árpád Vezér Gimnázium, Sárospatak
A matematikában és a természettudományokban, de a mindennapi életben is gyakran elôfordulnak olyan problémák, feladatok, amikor valaminek az értékét nem határozzuk meg pontosan, vagy azért, mert nincs rá szükségünk, vagy azért, mert nem is tudjuk meghatározni. Ezekben az esetekben megpróbálunk valamilyen becsült értéket adni. Sok esetben az érzékelt (látott, hallott, tapintott) jelenségeket a bennünk kialakult képességek alapján igyekszünk térben és idôben elhelyezni, becsüljük a nagyságot, a tôlünk való távolságot. Egyes emberekben nagyon pontos időérzék alakul ki, mások térbeli látása, tájékozódása kiváló.
Megtervezik, mennyi lesz a privatizációs bevétel vagy a gazdaság egyes ágazataiban a termelés, a fogyasztás, megbecsülik, mennyi jut az oktatásra a nemzeti jövedelemből. A mezőgazdaságban becsüljük a várható termést, a kárszakértő becsüli a kárt. Természetesen becsléskor bizonyos dolgoktól eltekintünk, így a becslési adatok nem minden esetben felelnek meg az adott terület szakemberei által igényelt szintnek.
Melyek azok az oktatási értékek, amelyek a becslési képesség növelésében rejtőznek?
Úgy gondolom, hogy a becslési képesség fejlesztése elősegíti a matematikai képességek és a mindennapi életben a helyes döntések számának növekedését. Ezért a tanulókat meg kell tanítani arra, hogy legyenek képesek a mindennapi életben használt méretek, mértékek, árak becslésére.
A mérést tanítjuk az iskolában, de a becslést nem, A Márai Sándor Gimnázium (Kassa) csapatának posztere Indul a vizesrakéta noha a becslési képesség fejlesztésének jelentős szerepe van az egyén más egyéb képességének fejlesztésében is. Az általános intelligencia, a matematikai képesség, készség olyan változók, amelyek kapcsolatban vannak a becslési képességgel.
Ha olyan becslési feladatot adunk, amelyben számolni is kell, akkor a számolási készségüket is növeljük.
Ha a tanuló jól becsül, növekszik az önértékelése, és természetesen az önkontrollja is: arra a kérdésre, hogy mennyi a gyalogos sebessége, nem fogadja el azt az eredményt, hogy 100 km/h, hanem keresi a hibát, hogy hol rontotta el a számolást.
Ezen tanulói képességek fejlesztésére vállalkozunk évek óta az Árpád Vezér Gimnázium és Kollégiumban (ÁVG), amikor megszervezzük ezt a nem mindennapi fizikai becslési versenyt. Becslési versenyt nem rendeznek sehol az országban, sőt a nagyvilágban sem rajtunk kívül. A verseny ötlete Kolláth Éva, Szeder László és jómagam fejében fogant meg, és Radnai Gyula egyetemi docens támogató közreműködésével jött létre.
Az első becslési versenyt 1995. január 25-én rendeztük Temesvár, Kassa, Királyhelmec, Nagykapos, Munkács, a Sárospataki Református Kollégium Gimnáziuma és az Árpád Vezér Gimnázium csapatának részvételével.
A 2001/2002-es tanévtől a Hátrányos Helyzetű Tanulók Arany János Tehetséggondozó Programjában (AJTP) tevékenykedő iskolák részvételével bővítettük a versenyt, így ma már egy időben, ám két - határon túli és AJTP-s - kategóriában versengenek a csapatok. A versenykiírás szerint hagyományosan egy-egy neves fizikus személyiségéről, munkásságáról emlékezünk meg. Az évek alatt már felidéztük Jedlik Ányos, Eötvös Loránd, Szilárd Leó, Mikola Sándor, Bolyai János, Öveges József, Lénárd Fülöp, Bánki Donát, Teller Ede és a fizika évében Albert Einstein munkásságát. Ennek formái színvonalas előadások, a versenyzők részéről megoldott (életrajzi és fizikai) totók, illetve otthon elkészített poszterek voltak.
A versenyfeladatsor az évek során kreatív feladatokkal is bővült, így ma már saját kezű eszközkészítést is elvárunk a csapatoktól. A verseny záró részét szóbeli becslési feladatok jelentik.
A sárospataki Árpád Vezér Gimnázium és Kollégium 2009. október 9-10-én 15. alkalommal rendezte meg a fizika becslési versenyt a határon túli testvériskoláink részvételével, az AJTP-iskolák pedig 9. alkalommal jöttek el a versenyre.
A verseny népszerűségét bizonyítja az a tény, hogy évről évre nő a csapatok száma. Ebben az évben 20 csapat vetélkedett egymással.
A versenyt 2009. október 9-én 14 órakor Tóth Tamás, az ÁVG igazgatója nyitotta meg. Megnyitójában megemlékezett a Nobel-díjas Békésy Györgyről és arról, hogy ebben az évben 300 éves a kísérleti fizika oktatása Sárospatakon, hiszen Simándi István 1709. június 29-én már kísérleti fizikai bemutatót tartott II. Rákóczi Ferenc fejedelemnek.
Álljon most itt az idei év versenyprogramja és a versenyfeladatsora a becslési verseny egyediségének, hasznosságának bizonyítékaként.
Az első napon Radnai Gyula, az ELTE docense tartott érdekes előadást Békésy György, a kutató címmel.
Ezen a délutánon nyílt meg a poszterkiállítás is: a 3 fős csapatok még otthon posztert készítettek Békésy György tevékenységéről, megadott szakirodalom alapján (Békésy György életéről és munkásságáról a Fizikai Szemle 1999/7, 1999/10 számaiból, Radnai Gyula: A megfigyelés öröme - Békésy György születésének 100. évfordulójára. Természet Világa 1999. június, Cornides István: Békésy György, a budapesti egyetem fizikaprofesszora. Természet Világa 1999. október).
A kreatív munka másik eleme a saját kezűleg készített vizesrakéta bemutatása volt. Nagyon sok ötletes és ügyes megoldású rakétát láthatott a zsűri és a közönség. Kit ne bűvölt volna el az az egyedi készítésű rakéta, amelyet a levegő helyett a szódabikarbóna fejlesztette gáz hajtott?
A verseny második napján a gyakorlati becslési feladatokkal, valamint a Békésy-totó és a fizikai totó megoldásával folytatódott a verseny.
Értékelés nélkül nem zárulhat verseny: Pántyané Kuzder Mária, Borsod-Abaúj-Zemplén megyei szak- tanácsadó, Radnay Gyula, az ELTE docense, Härtlein Károly, a BME Fizika Intézete demonstrációs laboratóriumának vezetője alkotta zsűri bírálta a csapatok feladat-végrehajtását.
A kiváló atmoszférájú vetélkedő versenyfeladatai a következők voltak.
|
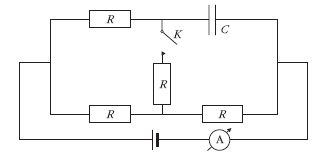
1. Az ábrán látható kapcsolásban minden ellenállás
R, a kondenzátor és az ampermérő ideális.
Hogyan változik az ampermérő árama, ha a K
kapcsolót zárjuk? 2 nem változik X csökken |
 |
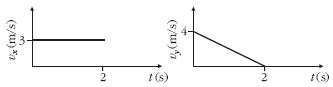
| 8. Egy test vízszintesen az Y,X síkban mozog. A test
sebesség-idő grafikonja az ábrán látható. Menynyi
a test gyorsulása a t = 2 s pillanatban? 2 1m/s2 X 1,5 m/s2 |
 |
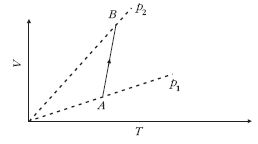
| 12. Az ábra állandó mennyiségű ideális gáz állapotváltozását
mutatja a V-T grafikonon. Hogyan
változik a gáz nyomása, ha A-ból B-be jut? 2 csökken a nyomás X nem változik a nyomás |
 |
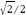-szerese. Hányszorosa a gyorsulása a
maximális gyorsulásnak?
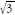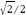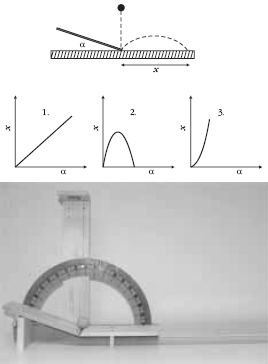
-szerese-szerese| 1. Ejtsünk h magasból pingponglabdát a lejtőre. Becsüljük
meg, hogy mekkora α szög esetén fog a pingponglabda a lehető legtávolabbra pattanni
a lejtő aljától adott h magasság esetén! A becsült szög: α = Végezd el a kísérletet! Becsüld meg, hogyan változik az X távolság a lejtő α szöge függvényében! |
 |
|
2. Két 40-50 cm hosszú vékony üvegcsövet deszkába
erősítünk. A két üvegcső közé égő gyufát tartunk. Mi
történik a cső felső végével? 2 A két cső közeledik egymáshoz. X A két cső távolodik egymástól. A becsült érték: Δl = ......... cm Becsüld meg, hogy a New Yorkban lévő 2040 m hosszú Verrazano-hídon az acélkábeleken függő úttest a nyári és téli hőmérsékletváltozás következtében mennyit süllyed! A becsült érték: Δl = ......... cm Becsüld meg, hogy a 314 m magas lakihegyi rádiótorony hossza mennyivel változik meg a téli -30 °C és a nyári 40 °C hőmérsékletváltozás következtében! A becsült érték: Δl = ......... cm |
 |
|
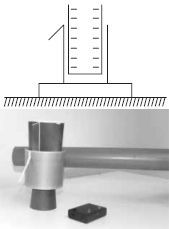
3. Szigetelőállványra szerelt konzervdoboz külső oldalára
alufóliacsíkot teszünk. Helyezzünk a konzervdobozba
egy negatív töltésű műanyagpoharat. Mi történik az alufóliával? Milyen töltés hatására? Indokold meg, miért! A konzervdobozt érintsük meg a kezünkkel. Mi történik az alufóliával? Vegyük ki a műanyagpoharat! Mi történik az alufóliával? Végezd el a kísérletet! |
 |
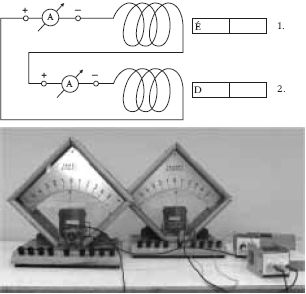
| 4. Két 1200 menetes tekercset és két ampermérőt az
ábrán látható módon kapcsolunk össze. Told be az
1-es mágnest! Figyeld meg, mi történik! Mi történik, ha a két mágnest egyszerre betoljuk? Becsüld meg, mi történik, ha az egyiket (1-es) betoljuk, a másikat (2-es) kihúzzuk a tekercsből! |
 |
|
5. Mérd meg a pénzérme tömegét a digitális mérleggel!
A pénzérme tömege: m = Ismerve a pénzérme tömegét a rendelkezésedre álló eszközök segítségével (pénzérme, vonalzó, ék) becsüld meg a vonalzó tömegét! Röviden írd le az eljárásod, becslésed lényegét! |
 |
|
6. Keresd meg a térképen Békésy György szülőházát!
A szülőháza száma:
Keresd meg Békésy György szobrát! Írd le a Békésy
szobor sorszámát! |
 |
|
Ki készítette az itt látható szobrot Békésy Györgyről?
A szobrot készítette: |
 |
| 7. Az ábra szerinti kapcsolásban mindegyik izzó azonos 220 V, 15 W. Állítsad sorba az izzók sorszámát a csökkenő fényerejük szerint! Kezdd azzal, amelyik legerősebben világít! Az izzók sorrendje csökkenő fényerő szerint: Becsüld meg, lesz-e olyan izzó, amelyik nem világít! Nem világít: Becsüld meg, vannak-e olyan izzók, amelyek fénye azonos! Kapcsold be és ellenőrizd becslésed! |  |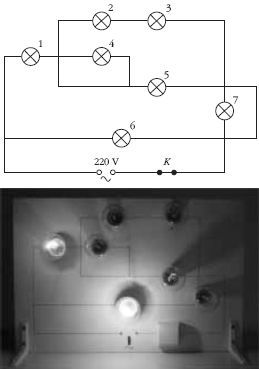
| 8. Az l hosszúságú fonálingát 90°-kal kitérítjük, majd elengedjük. A fonálinga golyója tökéletesen rugalmasan ütközik egy vele azonos golyóval, az ábra szerint. Becsüld meg, hogy mekkora s távolságra ér földet a golyó, ha h = l /4! A becsült érték: s = ...... cm. |  |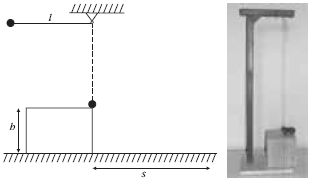
| 9. Békésy György doktori disszertációját Tangl Károlynál írta és vizsgálta, hogy az oldatok koncentrációváltozása következtében hogyan változik az oldatok törésmutatója. A rendelkezésedre álló eszközök segítségével mérd a törésmutatót! |  |
| 10. Becsüld meg, hogy melyik a feszültségforrás pozitív és negatív pólusa a feketedobozban! A pozitív pólus: A negatív pólus: Röviden indokold meg állításod! |  |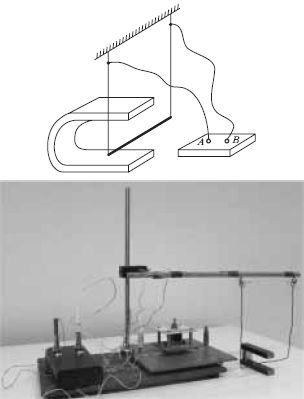
|
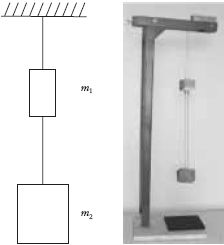
11. Az m és 2m tömegű testeket gumiszállal egymáshoz
kötjük, majd fonállal felfüggesztjük őket az
ábrán látható módon. A fonalat az m1 = m tömegű
test fölött elvágjuk. Mekkora lesz a testek gyorsulása
közvetlenül a fonál elvágása után?
Az m2 = 2m tömegű test a2 gyorsulása: A rendszer tömegközéppontjának a gyorsulása közvetlen a fonál elvágása után: |
 |
|
12. Az ábrán látható kapcsolásban a kapcsoló 1-es
állásban van már elég régen. C = 1000 µF, R = 30 kΩ,
U = 9 V. Mekkora lesz az egyes ellenállásokon átfolyó
áramerősség a kapcsoló 2-es állásba kapcsolása után
a) közvetlenül, b) hosszabb idő elteltével? Válaszoljunk a kérdésre, becsüljük meg, mi fog történni! Végezzük el a kísérletet!
|
 |
|
13. 1 m hosszú egyenes keresztmetszetű méterrudat
középen ékre támasztunk és vízszintes helyzetben
kiegyensúlyozunk. A méterrúd egyik felét kettévágjuk
és a levágott darabot a maradék részre helyezzük. Becsüld meg mennyivel kell eltolni az alátámasztást, hogy ismét egyensúlyban legyen! Végezd el a kísérletet! |
 |
|
14. Ha egy testet h1 magasból
márványlapra ejtünk, az
v1 sebességgel ütközik neki
a márványlapnak és v2 sebességgel
pattan vissza h2
magasra. A K ütközési tényező:
2 3 m X 4 m |
 |
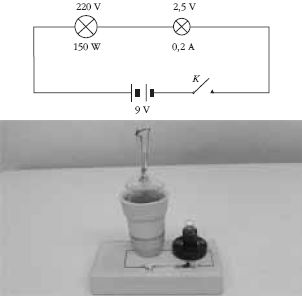
15. Csavarjuk be a búra nélküli 150 W-os hálózati
izzót a foglalatba! Sorba kapcsoltunk vele egy 2,5 V,
0,2 A-es zsebizzót és 9 V-os zsebtelepre kapcsoltuk.
Az izzó halványan világít.
|
 |
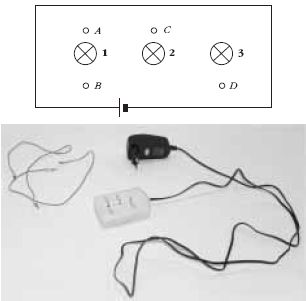
16. Becsüld meg, hogy milyen kapcsolás van az elektromos
feketedobozban! Teszteld A-B, A-C, B-C, B-D
és C-D összekapcsolásával!
|
 |
A fizika mindennel összefügg. Vajon felkelthetjük-e a sportot kedvelők érdeklődését a fizika iránt, ha azt kérdezzük tőlük, meddig javíthatók a rekordok a sportban? Hisszük, hogy igen, hisz az olimpiai jelmondatban is szerepel: "gyorsabban, magasabbra, erősebben".
Szakszerűen így hangzik a feladat: Becsülje meg, mennyi lehet a magasugrás rekordja! A versenyző futással nekirugaszkodik, maximálisan 10 m/s sebességre gyorsul fel, ismerve a függőleges hajítás maximális emelkedési magasságára vonatkozó összefüggést
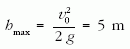
adódik. Ezt a magasságot még messze nem érték el sportolóink.
Tehát még van mit tenni a versenyzőknek, edzőknek, de úgy gondolom, nekünk fizikát tanító pedagógusoknak is.
