BEÉGETHETIK-E NAPSÜTÉSBEN A LEVELEKET A RÁJUK TAPADT VÍZCSEPPEK? EGY TÉVHITEKKEL TERHES BIOOPTIKAI PROBLÉMA TISZTÁZÁSA
I. rész: Napfény forgásszimmetrikus vízcseppek általi fókuszálásának számítógépes vizsgálata

Egri Ádám, Horváth Gábor - ELTE, Fizikai Intézet, Biológiai Fizika Tanszék
Horváth Ákos - Max Planck Meteorológiai Intézet, Hamburg
Kriska György - ELTE, Biológiai Intézet, Biológiai Szakmódszertani Csoport

Egy a kertészetben és növényvédelemben széles körben elterjedt vélekedés szerint a növényeket délben, tűző napon nem szabad locsolni. Ennek az egyik leggyakoribb magyarázata, hogy a levelekre tapadt vízcseppek nagyítólencsékként a napfényt összegyűjtve égési sérüléseket okozhatnak a leveleken. A Világhálón böngészve számos kertészettel és növényvédelemmel kapcsolatos olyan honlapra akadtunk, amelyek azzal a kérdéssel is foglalkoztak, hogy képesek-e a vízcseppek fényfókuszálás által sérüléseket okozni a növényeken. Tapasztalatunk szerint ezen oldalak mintegy 77%-a válaszolt igenlően a következő kérdésre: Kiégethetik-e a napsütötte vízcseppek a leveleket? Itt most csak két szélsőséges véleményt idézünk:

• A levélégés fő okai a vízpermet, a trágyalé vagy különféle vegyszerek lehetnek, amelyek a lombozatra kerülnek meleg nyári időben. Ekkor az történik, hogy a levélen ülő vízcsepp úgy viselkedik, mint egy nagyítólencse - a napfényt a levélre fókuszálja, így az túlmelegszik, majd beég. Hasonlóan ahhoz, mint mikor egy nagyítólencsével megégetünk egy darab papírt. ( http://www.searle.com.au/leafburn.htm)
• Itt a meleg nyári idő, amikor az embereknek azt szokták ajánlani, hogy ne locsoljanak napsütésben. A legkézenfekvőbb ok, hogy ekkor túl nagy a párolgási vízveszteség. Olyan vélemények is hallhatók, hogy a napsütésben való öntözés megégeti a növényeket, mert a vízcseppek összegyűjtik a napfényt. [...] Valóban megéghetnek a növények a vízcseppek miatt? Nem hiszem, hogy egy vízcsepp olyan hatékony nagyítólencse volna. Egy vízcsepp fókuszpontja határozottan a levél alatt van. Ahogy a levélen ülő csepp mérete csökken, a fókuszpontja fölfelé mozog, viszont kevesebb fényt tud összegyűjteni. Tehát én nem fogadom el a nagyítólencse-elméletet. (http://www.cahe. nmsu.edu/ces/yard/1999/062899.html)

E biooptikai probléma az (alap-, közép- és felsőfokú) oktatásban is gyakran előfordul. Példaként idézzük a 2006. május 15-i gimnáziumi fizika érettségi feladatsor egyik feladatát, amit az Oktatási Minisztérium adott ki:

Nyáron, déli napsütésben nem ajánlatos a kertben locsolni, mert "megégnek" a növények levelei. Az alábbi magyarázatok közül csak egy fogadható el, melyik?

1. ) A gyorsan párolgó víz hirtelen lehűti a növényt. A fagyás tünetei megegyeznek az égésével.
2. ) A vízcseppek gyűjtőlencseként viselkednek, és a levelekre fókuszálják a napfényt.
3. ) Az elpárolgó víz forró gőze okoz "égési tüneteket".

A válaszok közül a B-t fogadták el helyesnek. Mindebből jól látszik, hogy sok laikus és szakember is úgy gondolja, öntözés vagy eső után a vízcseppek képesek megégetni a leveleket napsütésben. Valójában ez egy régi környezetoptikai probléma, amelynek megoldása egyáltalán nem egyszerű.

Egy másik hasonló kérdés, hogy a vízcseppekkel borított emberi bőr szenvedhet-e sérüléseket napozás közben. Az e kérdéssel is foglalkozó, általunk meglátogatott bőrgyógyászati és kozmetikai honlapok 89%-a pozitívan válaszolt arra a kérdésre, hogy: képesek- e a napsütötte vízcseppek megégetni az emberi bőrt. De az erdőtüzekkel foglalkozó szakirodalomban is föl-fölbukkan az a vélekedés, hogy e tüzeket vízcseppek kelthetik azáltal, hogy az elszáradt növényzeten maradt esőcseppek összegyűjtik a napfényt.

A szóban forgóhoz leginkább hasonló abiotikus optikai probléma a fény törése hulló esőcseppeken, ami a jól ismert szivárványt eredményezi. Bár a szivárvány irodalma igen nagy [1-8], a kapcsolódó elméletek és kísérletek kizárólag csak gömb alakú vagy gömbölyded vízcseppekre vonatkoznak, mivel a hulló esőcseppek ilyenek. Élő szervezetekben hasonló problémára akadunk a halak szemében: A halak szemlencséje gömb alakú, helyfüggő törésmutatóval [9]. Különféle halak szemlencséje optikájának megismerése céljából elméleti, kísérleti és számítógépes vizsgálatokat végeztek. Ezek egyikében egy optikailag homogén, gömb alakú szemlencse fénygyűjtőképességét modellezték [10], míg mások sugárfüggő törésmutatóval tették ugyanezt [11].

Tudomásunk szerint levelekhez tapadt vízcseppek fényfókuszálását behatóan sem kísérleti, sem pedig elméleti úton eddig nem tanulmányozták. Hogy ezt az űrt betöltsük, számítógépes modellezést és kísérleteket végeztünk a napsütötte levelekhez tapadt vízcseppek fénygyűjtésének tanulmányozása céljából [12]. Cikkünk I. részében számítógépes vizsgálataink eredményeit foglaljuk össze. Mivel az a fényintenzitás, aminél már éppen beég a levél, ismeretlen, ezért a szóban forgó biooptikai probléma nem oldható meg pusztán számítógépes modellezéssel. Ennélfogva kísérleteket is végeztünk napsütötte leveleken ülő vízcseppekkel. E kísérleti eredményeinket cikkünk II. részében közöljük.

Számítási módszerek

Csak forgásszimmetrikus, azaz vízszintes levélen ülő vízcseppeket tanulmányoztunk különböző nedvesítési szögek mellett. Három különböző növényfaj (berkenye: Sorbus aucuparia, platán: Platanus hybrida, juhar: Acer platanoides) leveleit vízszintes üveglapra rögzítettük átlátszó ragasztószalaggal. Minden levélre egy kevés tiszta csapvizet helyeztünk el egy szemcseppentővel. Az így kialakuló vízcsepp méretét és alakját az határozta meg, hogy hány cseppet juttattunk ugyanarra a helyre a cseppentővel. A levélen ülő vízcseppet a fényképezőgép vízszintes optikai tengelye mellett oldalról lefényképeztük (3.a, 4.a, 5.a ábrák). A vízcsepp felső és alsó részének főtengelymetszete (ami a fényképeken látszik) két különböző függvénnyel írható le. A cseppmérettől és a nedvesítési szögtől gyakorlatilag függetlenül, a csepp felső fele nagyon jó közelítéssel egy ellipszis:

ahol x és y a derékszögű Descartes-koordináták a vízszintes síkban; B és C pedig az ellipszis fél nagy-, illetve kistengelye, f -et pedig a függőleges z tengelyen mérjük. Ha a vízcsepp és a levél közti, vízszintestől mért ? nedvesítési szög nem sokkal nagyobb, mint 90°, akkor a csepp alsó fele is jól közelíthető egy ellipszissel (f < 0). Ha α jóval nagyobb, mint 90°, akkor a csepp alsó felét jó közelítéssel a következő g (r ) függvény írja le:

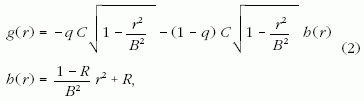
ahol B és C ismét az ellipszis féltengelyei, a q paraméter (q = 0 vagy 1) pedig azt határozza meg, hogy az ellipszist leíró f (r ) függvényt megszorozzuk-e a h(r) parabolával (q = 0), vagy nem (q = 1). A h(r) kifejezésében R = h(r =0).

A vízcseppbeli sugármenet követése: vízcseppek fénygyűjtőképessége

Üljön egy forgásszimmetrikus vízcsepp egy vízszintes levélen, amit a napfény világít meg a vízszintestől mért θ szoláris elevációszögben az 1. ábra szerinti módon. Egy adott fénysugár P₀ = (x₀, y₀, z₀) kiindulási helye és kezdeti irányának e₀ = (e_0x, e_0y, e_0z) egységvektora ismert (e₀ = 1). A fénysugár tetszőleges pontjának helyvektora paraméteres formában a következő:

ahol t a kontrollparaméter. A vízcsepp felszínének alakját az S(x, y,z) = 0 egyenlet írja le. A bejövő fénysugár és a cseppfelület metszéspontjának koordinátáit a következő egyenlet határozza meg:

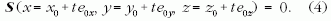
Ha (4)-nek két valós megoldása van, akkor a fénysugár megtörik a vízcseppen. E két (t₁, t₂) megoldás közül a kisebbikre van szükség, mivel ez határozza meg a fénytörés helyét, P₁-et. Innen a sugár a cseppben halad tovább (1. ábra). Ha a vízcsepp felületét leíró függvény D(x, y), akkor a cseppfelület N normálvektora (N = 1) így adható meg:

ahol × vektoriális szorzatot jelent. Jelöljük a vízcsepp felszínére érkező fénysugár irányának egységvektorát e₀-lal, a megtört sugárét pedig e₁-gyel (1. és 2.a ábra). A Snellius-Descartes-féle törési törvényt alkalmazva:

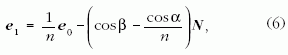
ahol α és β rendre a beesési és törési szögek (2.a ábra), és n = 1,33 a víz átlagos törésmutatója a 400 nm ≤λ ≤ 750 nm látható hullámhossztartományban. A vízcseppből kilépő sugármenetkor a víz-levegő határfelületre eső sugár irányának egységvektora e₁, míg a levegőben tovahaladó megtört sugáré e₂ (1. és 2.b ábra). Ekkor az előző esethez hasonlóan a megtört sugár irányának egységvektora:

ahol δ és γ rendre a beesési és törési szögek (2.b ábra).

A fönti formulák használatával adott cseppalaknál és θ szoláris elevációszögnél 216 000 000 párhuzamos fénysugár cseppbeli pályáját számítottuk ki. Minden sugarat addig követett a számítógépes program, míg a levélfelületet képviselő vízszintes sík P₃ pontjába nem ütközött (1. ábra). E vízszintes síkot 900 × 600 elemi cellára osztottuk föl. Ha egy cellába érkezett be egy fénysugár, akkor a cellához rendelt m egész szám értéke eggyel nőtt. Így egy adott cella m értéke arányos az azon helyen várható I fényintenzitással. (Ha a levegő-víz határfelületről visszavert, s a Fresnel-formulákkal számolható fényintezitást is figyelembe vennénk, akkor ez az I értékében legföljebb néhány százalékos eltérést okozna, de igen megnövelné a számítások idejét, ezért lemondtunk erről.) Egy adott cellában a vízcsepp fénygyűjtőképességét a Q = m/m₀ értékkel definiáltuk, ahol m0 az az érték, ami úgy adódna, ha a csepp nem létezne. A számítások eredményeként tehát egy olyan kétdimenziós mátrixot kapunk

(ez képviseli a vízszintes levélfelületet a csepp alatt), amelynek minden cellájában egy Q szám van, ami függ a bejövő fény vízszintestől mért θ szögétől és a csepp alakjától.

A levelek által elnyelt, vízcsepp által fókuszált fény intenzitása: a növényi levél fényelnyelési tényezője

A vízcseppekkel borított növényi levelek esetleges beégését a cseppek által fókuszált fény túl nagy intenzitása okozhatja. Ha egy levélre eső napfény spektruma I_Nap(λ,θ) (7.a ábra), a levélszövet fényelnyelési spektruma pedig A(λ) (7.b ábra) - ahol λ a fény hullámhossza, θ pedig a szoláris elevációszög -, akkor a levél által elnyelt, vízcsepp által fókuszált fény intenzitása egy adott helyen:

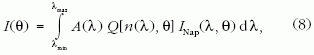
ahol Q[n(λ),θ] a vízcsepp fénygyűjtőképessége, ami függ a θ szoláris elevációtól és a víz hullámhosszfüggő n(λ) törésmutatójától. I(θ) megadja az egységnyi idő alatt, egységnyi felületen elnyelt energiát adott θ mellett. I_Nap(λ,θ) a látható hullámhossztartományban maximális (7.a ábra), ezért csak a λ_min = 400 nm ≤ λ≤λ_max = 750 nm tartománnyal foglalkoztunk. Mivel a spektrum e tartományában a víz törésmutatója csak kicsit változik, ezért az n(λ) ≈ állandó = n_víz = 1,33 közelítést alkalmaztuk. Ez azért volt fontos, mert különben egy adott cseppalaknál a Q fénygyűjtőképességet λ függvényében is meg kellett volna határozni minden θ-nál, ami rengeteg számítást igényelt volna. Ha tehát n = 1,33 és a 400 nm ≤ λ ≤ 750 nm hullámhossztartományra korlátozódunk, akkor I (θ) a következőképpen számolható:

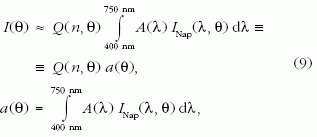
ahol a(θ)-t a levél "szoláris fényelnyelési tényező"-jének nevezzük. Adott cseppalakra kiszámítottuk a Q(n,θ) mátrixot. Ha egy cseppmentes vízszintes levelet tekintünk a vízszintestől mért θ szögben beeső I_Nap(λ,θ) spektrumú fénynyaláb mellett, akkor a levél által elnyelt fény intenzitása:

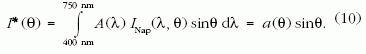
Így egy vízcseppes levél I(θ)/I*(θ) = Q(n,θ)/sinθ-szor nagyobb intenzitást nyel el a fókusztartományban a cseppmentes esethez képest. A napfény I_Nap(λ,θ) spektrumait a MODTRAN (MODerate resolution TRANsmittance) légköroptikai számítógépes program 3,7-es verziójával számítottuk az 1976-USA normál légkörmodell mellett [13, 14]. Az I_Nap(λ,θ) megadja, hogy mennyi napenergia áramlik át egységnyi idő alatt, egységnyi felületen, egységnyi hullámhossztartományban (7.a ábra).

Számítógépes eredmények

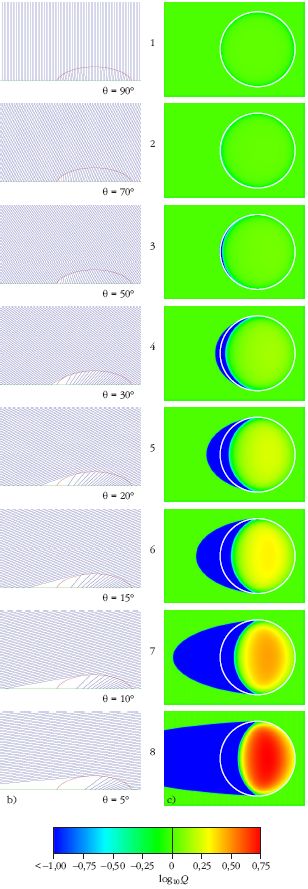
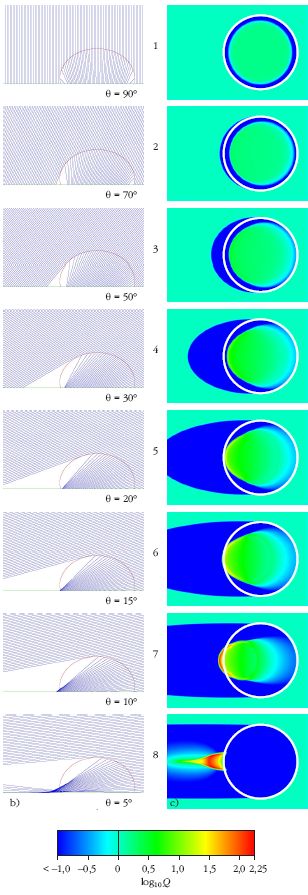
A 3.a ábrán egy tipikus vízcsepp látható vízszintes juharlevélen (Acer platanoides). E csepp eléggé lapos, mivel kicsi a nedvesítési szög (α < 90°) a víz és a levél között. A 3.b ábra a vízcsepp függőleges főtengelymetszetében haladó fénysugarakat mutatja a bejövő fénynyaláb θ szögének függvényében. A 3.c ábra a vízcsepp Q fénygyűjtőképessége 10-es alapú logaritmusának eloszlását szemlélteti a levél vízszintes síkjában. A cseppnek köszönhetően θ < 50° esetén megjelenik egy sarló alakú árnyékos terület, ahol log₁₀Q < -1. A 35° < θ < 5° tartományban ez az árnyék azon körön belülre esik, ahol a csepp érintkezik a levéllel, míg ha θ < 30°, akkor az árnyék nagy része kívül esik e körön a Nappal ellenkező oldalon (anti-Nap). θ < 10° mellett az árnyékos terület hosszan elnyúlik az anti-Nap felé.

A 3.c ábra szerint adott θ mellett a levél vízszintes síkján a legmagasabb Q fénygyűjtőképességű pont és környezete - amit a továbbiakban fókusztartománynak hívunk - egy ellipszishez hasonló alakú terület. Ahogy θ csökken, Q_max nő. Mivel a fókusztartomány minden θ-ra a lapos csepp körvonalán belül marad, a vízcsepp minden esetben hűti a fókusztartományt. Másrészt egy ilyen lapos cseppre Q_max meglehetősen kicsi: A 6.a ábra szerint, ha θ > 5°, akkor log₁₀Q < 0,75, azaz Q < 5,6.

Ez azt jelenti, hogy a fókusztartományra a direkt napfényénél csak 5,6-szer nagyobb fényintenzitás esik. A vízhűtésnek köszönhetően, és mivel Q nagyon kicsi, a napégés esélye egy ilyen lapos csepp esetében elenyészően alacsony.

A 4.a ábra egy vízszintes platánlevélen (Platanus hybrida) ülő vízcseppet mutat. E csepp megközelítőleg félgömb alakú, mert a nedvesítési szög majdnem derékszög (α ≈ 90°). A nagyobb görbületeknek köszönhetően e vízcsepp jobban összegyűjti a napfényt (4.b ábra), mint a 3. ábra szerinti lapos csepp. Ezért az árnyékos terület θ > 60° esetén gyűrűszerű, ami θ < 60° mellett sarlószerűen kidudorodik a 4.c ábrán látható módon. Ha θ > 60°, akkor az árnyék nagy része a csepp és a levél érintkezési felületének körén belülre esik, míg ha θ < 55°, akkor az árnyék zöme e körön kívül, a csepp nappal ellenkező oldalán található. θ < 20° esetén az árnyék nagyon elnyúlik az anti-Nap felé.

Ahogy a 4.c ábrán látszik, a fókusztartomány a levélen szinte mindig sarló alakú. Ahogy θ csökken, Q_max nő. Mikor θ > 1°°, a fókusztartomány a csepp és a levél érintkezési felületének körén belül van, így a vízcsepp hűti e tartományt. θ < 15° mellett a fókusztartomány kívül esik e körön. Mivel ekkor nincs vízhűtés, és mert a fókusztartományban a legnagyobb a fényintenzitás, ezért a levél esetleg égési sérülést szenvedhet. Azonban Q_max csak mérsékelt értékeket vesz föl: A 6.b ábra szerint θ > 5°-ra log₁₀Q < 2,25, azaz Q < 177,8. Tehát ekkor a fókusztartományra a direkt napfényénél nagyjából 178-szor nagyobb fényintenzitás esik. Egy ilyen félgömb alakú vízcsepp sokkal hatékonyabban gyűjti a napfényt, mint a 3. ábra lapos cseppje, miáltal a napégés valószínűsége is nagyobb. Annak eldöntéséhez, hogy a direkt napfény intenzitásának 178-szorosa elegendő-e a levél beégéséhez, kísérletekre van szükség.

Az 5.a ábrán egy vízszintes berkenyelevélen (Sorbus aucuparia) ülő vízcsepp látható. E csepp nagyon gömbölyű a nagy nedvesítési szög (α ≈ 145°) miatt, és éppen ezért erősen megtöri és összegyűjti a napfényt (5.b ábra). A gyűrűszerű árnyékos terület θ > 50° esetén jelenik meg, míg ha θ < 40°, akkor az anti-Nap felé elnyúlik (5.c ábra). Mikor θ > 50°, az árnyék jelentős része a csepp és a levél érintkezési körén belülre esik, míg ha θ < 40°, akkor az árnyék fokozatosan kikerül e körből. θ < 23° mellett az érintkezési kör teljesen árnyékban van, és a rajta kívüli árnyékos rész jelentősen megnyúlik az anti-Nap irányában.

Az 5.c ábra szerint a levélen a fókusztartomány ovális, ha θ > 50°. A fókusztartomány θ ≈ 30°-nál nyolcas alakot vesz föl, amelynek maximális fényintezitású része sarló alakú. θ ≈ 23° esetén a sarló alakú fókusztartomány merőleges az antiszoláris meridiánra, míg ha θ < 16°, akkor a fókusztartomány egy elnyújtott ellipszis, amelynek nagytengelye párhuzamos az antiszoláris meridiánnal. Ha θ > 50°, akkor a fókusztartomány nagy része a levéllemez és a vízcsepp érintkezési körén belül van, azaz a vízcsepp hűti a levelet. Viszont θ < 40° mellett a fókusztartomány kiesik e körből, és ezért a csepp nem hűti a levél legintenzívebb fényt kapó tartományát. Mindemellett a θ szoláris eleváció e szögtartományában éri a levelet a legnagyobb fényintenzitás, ezért nagyban megnő a beégés esélye. A 6.c ábra szerint, ahogy a θ szoláris eleváció 90°-ról 0°-ra csökken, a gömbölyded vízcsepp fénygyűjtőképességének 10-es alapú logaritmusa először log₁₀Q = 2,55-ra nő, utána 2,05-ra csökken, majd ismét növekszik egészen 2,3-ig, majd lecsökken 1,4-re, végül újra elkezd nőni. Tehát Q(θ)-nak két helyi maximuma van: Q_max1(θ=23°) = 354,8, és Q_max2(θ=13°) = 199,5. Mindez annyit jelent, hogy e két esetben a fókusztartományt a direkt napfényénél 355-ször és 200-szor nagyobb fényintenzitás éri.

Így a levél beégésének esélye az 5. ábra vízcseppének jelenlétében sokkal nagyobb, mint a 3. ábra lapos vagy a 4. ábra félgömb alakú cseppje esetén. Azt, hogy a direkt napfény intenzitásának 200 vagy 355-szöröse elegendő-e a levelek sérüléséhez, csak kísérletekkel lehet eldönteni.

A 7.a ábra a napfény I_Nap(λ,θ) spektrumát mutatja különböző θ szoláris elevációszögekre, míg a 7.b ábrán egy átlagos zöld levél A(λ) fényelnyelési spektruma látható, ami a bab-, spenót-, fehérrépa- és dohánylevél elnyelési spektrumának átlagolásából származik [15]. E spektrumok fölhasználásával számítottuk ki az átlagos zöld levél

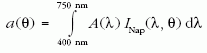
szoláris fényelnyelési tényezőjét, amely a 7.c ábrán látható. E mennyiség azért fontos, mert ennek segítségével tudjuk kiszámítani a zöld levél által elnyelt, vízcsepp által fókuszált

fényintenzitást. A 6. ábra Q(n_víz,θ) és a 7.c ábra a(θ) függvényeinek fölhasználásával megkaphatók a 8. ábrán látható I(θ) függvények, amelyeket a vízszintes juhar-, platán- és berkenyelevélen ülő vízcseppekre számítottunk.

A juharlevélen laposan elterülő vízcsepp esetében, amint a θ szoláris elevációszög csökken, I (θ) monoton nő, de a log₁₀I nem haladja meg 2,85-ot (8.a ábra). Eszerint egy vízszintes juharlevelet a legnagyobb fényintenzitás naplementekor éri, amikor a Nap a horizonthoz közel tartózkodik. Ugyanez érvényes egy vízszintes platánlevélen ülő félgömb alakú vízcseppre, melyre log₁₀I = 4,37, ha θ = 5° (8.b ábra). Tehát naplementekor a félgömb alakú vízcseppet tartó platánlevélre nagyjából 10^4,37-2,85 = 10^1,52 ≈ 33-szor nagyobb intenzitású fény jut a fókusztartományban, mint a lapos vízcsepp esetén (8.a ábra). Másrészt viszont a vízszintes berkenyelevélen ülő gömbölyű vízcsepp esetében az I (θ) függvénynek két helyi maximuma van: az egyik θ = 13°-nál log₁₀I = 4,7 maximumértékkel, a másik pedig θ = 23°-nál log₁₀I = 5,1 maximummal (8.c ábra). Tehát θ = 13° és 23° mellett e gömbölyű vízcseppnek köszönhetően a levelet 10^4,7-2,8 = 10^1,9 ≈ 79-szer és 105,1?2,7 = 102,4 ≈ 251-szer nagyobb fényintenzitás éri, mint a lapos vízcsepp esetén (8.a ábra).

A számítógépes modellezés eredményeinek elemzése

A 6.c és 8.c ábrákon látható a vízszintes berkenyelevélen ülő gömbölyded vízcsepp Q fénygyűjtőképessége, és a csepp által fókuszált, levél által elnyelt I fényintenzitás. Mindkét görbének egy-egy maximuma van θ₁ = 13° és θ2 = 23°-os szoláris elevációnál. E két maximum optikai oka a vízcsepp asztigmatizmusa, ami azt jelenti, hogy a nem pontosan gömb alakú vízcsepp két különálló fókusztartománnyal bír: Az első (θ1 = 13°-nál, a csepptől távolabb) és a második (θ₂ = 23°-nál, a csepphez közelebb) fókusztartomány rendre a vízcsepp vízszintes és függőleges főtengelymetszetében haladó fénysugaraknak köszönhetően alakul ki. Ennek eredményeképpen az első és a második fókusztartomány az antiszoláris meridiánnal párhuzamosan, illetve arra merőlegesen elnyújtott. Mindez tisztán látszik az 5.c/6 (θ₁ = 13°) és 5.c/4 (θ₂ = 23°) ábrákon.

A 6. és 8. ábrákon jól látszik, hogy egy adott θ-nál minél víztaszítóbb a vízszintes levél (minél nagyobb a nedvesítési szög), annál nagyobb a rajta ülő vízcsepp felületének görbülete, és egyben a csepp fénygyűjtőképessége is (ha θ > 10°). Egyszóval, minél inkább vízlepergető a levél, annál inkább fennáll a veszélye, hogy a levélen megtapadó vízcseppek a napfényt fókuszálva beégetik a növényt. Másrészről viszont, minél víztaszítóbb egy levél, annál könnyebben lepereg róla a víz, tehát csökken a napégés veszélye. Az eddigi eredményeink alapján a következőket szűrhetjük le:

• A napsütötte vízszintes növényi leveleken erősen megtapadó vízcseppeknek (a kis nedvesítési szögnek köszönhetően) kicsi a görbületük (így nem jelentős a fénytörőképességük), a fókusztartományuk mélyen a levéllemez alá esik (3., 4., 6.a, 6.b, 8.a, 8.b ábrák), így nem okoznak égési sérüléseket a levélszövetben.
• Habár napsütésben a nagy fénytörőképességű gömbölyded vízcseppek fókusztartománya a szoláris eleváció széles tartományában közel esik a vízszintes levélfelülethez, s így égési sérüléseket okozhatnának a levélen (5., 6.c, 8.c ábrák), e vízcseppek könnyen leperegnek a levélről, amelyek általában nem is vízszintes helyzetűek. Tehát e gömbölyded vízcseppek sem okoznak napégést a levélszövetben.
• Ennélfogva a vízcseppek által fókuszált napfény rendszerint nem képes beégetni a leveleket, függetlenül a cseppek alakjától, méretétől és a napállástól
• Az egyetlen kivétel az, ha a vízcseppet víztaszító növényi szőrök tartják a levél felszíne fölött, miáltal a csepp fókusztartománya pontosan a levélre eshet. Cikkünk II. részében erre mutatunk egy konkrét példát.
• Nagyon hasonló következtetések vonhatók le azon két rokon biooptikai problémával kapcsolatban is, hogy (i) vizes bőrrel való napozáskor érheti-e hősérülés az emberi bőrt, és (ii) okozhatnak-e tüzet kiszáradt növényzetre tapadt napsütötte vízcseppek.

Vizsgálatainkat az a közkeletű vélekedés inspirálta, hogy déli napsütésben nem szabad a növényeket öntözni, mert a leveleikre tapadt vízcseppek által fókuszált napfény megégetheti a leveleket. A föntiek és a cikkünk II. részében taglalt eredmények alapján azt mondhatjuk, hogy ez nem más, mint egy tévhit, mítosz. A 8.c ábra alapján a beégés veszélye θ ≈ 23°-os szoláris elevációnál, délelőtt vagy délután a legnagyobb, nem pedig délben, amikor θ maximális (Magyarországon délben θ_max ≈ 67°). Fölmerül a kérdés: honnan ered e mítosz? A Világhálón a következő olyan magyarázatokat találtuk, amelyek nem a vízcseppek által fókuszált napfénnyel indokolják a növények égési sérülésekhez hasonló barna foltjait, viszont könnyen összefüggésbe hozhatók ezzel:

• Régi kertészeti tanácsnak számít, hogy a kertet soha se öntözzük napközben, mivel a virágok, különösen az egynyáriak könnyen tönkremehetnek, ha vizet kapnak, amíg teljesen nyitva vannak a szirmaik a nappali órákban. E sérülés fő oka inkább a súlyos vízcseppeknek a finom virágszirmokhoz való ütődése, mintsem az erős napfény. (http://www.bonsai4me.com/Basics/Basics%20Bonsai%20Myths%20Misting.htm).
• Napsütésben való locsoláskor a növények nem tudják az összes kiöntözött vizet hasznosítani, mivel a víz jó része elpárolog, és nem jut el a gyökerekhez. (http://forums.gardenweb.com/forums/load/pests/msg0712193332527.html?6).
• Annak két fő oka, hogy napközben, főleg pedig délután nem szabad locsolni a növényeket, az, hogy a szelek délután a legerősebbek, és a víz párolgása is ekkor a leggyorsabb a délutáni nagy hőségben. A párolgás a leghidegebb napszakban, kora reggel a leglassúbb. A legszélcsendesebb napszak általában ugyancsak a reggel. Így kora reggel érdemes öntözni, mert ekkor a kilocsolt víz túlnyomó részét a növények hasznosítják a hűvös és szélcsendes időbeni minimális párolgási veszteségnek köszönhetően. (http://www.cahe.nmsu.edu/ces/yard/1999/062899.html).
• Annak egyik oka, hogy kora reggel érdemes öntözni, az, hogy habár napközben a növények nedves levelei megszáradnak, de a mélyebb talajrétegekben hosszabb ideig megmarad a víz. A levelek szárazon maradása jelentősen csökkenti a gombásodás veszélyét. Mindezt azzal is elősegíthetjük, hogy nem locsolunk minden nap. Ha vízzel jó mélyen átáztatjuk a talajt, akkor nem szükséges naponta öntözni, és a gombák is csak kevésbé képesek megfertőzni a növényeket. (http://www.cahe.nmsu.edu/ces/yard/1999/062899.html).

Vajon az emberi bőrön megtapadt vízcseppek jelentenek- e veszélyt napozás közben? Ezt tételezi fel sok bőrgyógyászati és kozmetikai honlap. Ha a bőr nem zsíros, akkor a nedvesítési szög a bőr és a víz között viszonylag kicsi, a bőrre tapadt vízcsepp lapos, ezért a fókusztartománya mélyen a bőr alá esik, így a bőrégés veszélye kizárható. Bár az ultraibolya (UV) sugárzás felerősödik a vízcsepp fókuszálása által, s így növelheti a bőrrák kialakulásának esélyét, a napfény UV összetevőjének egy részét a víz elnyeli, miáltal a bőrhöz tapadt vízcseppek még védelmül is szolgálhatnak a veszélyes UV-sugárzás ellen. E probléma tehát meglehetősen bonyolult, és a jövőben érdemes lenne kísérletekkel tanulmányozni. Ugyanakkor, ha a bőr zsíros - például naptejjel van bekenve -, akkor a rajta ülő vízcseppek a nagy nedvesítési szög miatt gömbölyűek, ezért könnyen le is peregnek, miáltal az általuk fókuszált napfény miatti égési bőrsérülés esélye minimális.

Cikkünk II. részében megmutatjuk, hogy víztaszító levélszőrök által tartott napsütötte vízcseppek okozhatnak égési sérüléseket a levélen, ha a fókusztartomány pont a levélre esik. Ehhez hasonló a helyzet, mikor emberi szőrzet tart vízcseppeket a bőr fölött: ha a cseppek fókusztartománya a bőrre esik, akkor a nagy intenzitású fókuszált fény (UV-összetevővel vagy anélkül) károsíthatja a bőr szöveteit. Ennek persze az a feltétele, hogy a napozó személy ne mozogjon, hiszen máskülönben a szőréhez tapadt vízcseppekre mindig máshonnan érkezik a napfény, ami azt eredményezi, hogy a cseppek fókusztartománya mindig a bőr más részeire kerül. Ezek alapján az emberi bőrhöz tapadt napsütötte vízcseppek miatti égési sérülésekkel kapcsolatos vélemények egészséges szkepszissel kezelendők.

Teljesen hasonló jelenség fordul elő, amikor eső után vízcseppek tapadnak a kiszáradt növényzethez, például szalmához, szénához, avarhoz vagy száraz fűhöz. Ha egy vízcsepp fókusztartománya a száraz növény felszínére kerül, akkor az intenzív napfény elvileg okozhat tüzet. Viszont eső után az eredetileg száraz növényzet nedvessé válik, és míg újra kiszárad, a vízcseppek is elpárolognak. Így a száraz növényi részekhez tapadt napsütötte vízcseppek okozta erdőtüzekkel kapcsolatos véleményeket ennek megfelelő kritikával érdemes kezelni.

Irodalom

1. R. DesCartes: Oeuvres de Des Cartes. La Géometrie. Livre 2, J. Maire, Leyden, 1637.
2. G. B. Airy: On the intensity of light in the neighbourhood of a caustic. Transactions of the Cambridge Philosophical Society 6 (1838) 379-403.
3. V. Khare, H. M. Nussenzweig: Theory of the rainbow. Physical Review Letters 33 (1974) 976-980.
4. H. M. Nussenzweig: The theory of the rainbow. Scientific American 236 (1977) 116-127.
5. G. P. Können, J. H. de Boer: Polarized rainbow. Applied Optics 18 (1979) 1961-1965.
6. R. T. Wang, H. C. van de Hulst: Rainbows: Mie computations and the Airy approximation. Applied Optics 30 (1991) 106-117.
7. R. L. Lee: Mie theory, Airy theory, and the natural rainbow. Applied Optics 37 (1998) 1506-1519.
8. Cserti J.: A szivárvány fizikája: esőcseppek fényszórási jelenségei. I., II., III. rész. Fizikai Szemle 55 (2005) 297-302, 349-355, 422-427.
9. M. F. Land, D.-E. Nilsson: Animal Eyes. Oxford University Press, Oxford, UK, 2002, p. 221.
10. W. S. Jagger: The optics of the spherical fish lens. Vision Research 32 (1992) 1271-1284.
11. R. H. H. Kröger, M. C. W. Campbell, R. D. Fernald, H.-J. Wagner: Multifocal lenses compensate for chromatic defocus in vertebrate eyes. Journal of Comparative Physiology A 184 (1999) 361-369.
12. Á. Egri, Á. Horváth, G. Kriska, G. Horváth: Optics of sunlit water drops on leaves: conditions under which sunburn is possible. New Phytologist (2009) doi: 10.1111/j.1469-8137.2009.03150.x
13. COESA: U. S. Standard Atmosphere. U. S. Government Printing Office, Washington, D.C. 1976.
14. A. Barducci, F. Castagnoli, D. Guzzi, P. Marcoionni, I. Pippi, M. Poggesi: Solar spectral irradiometer for validation of remotely sensed hyperspectral data. Applied Optics 43 (2004) 183-195.
15. . R. A. Moss, W. E. Loomis: Absorption spectra of leaves. I. The visible spectrum. Journal Paper number J-2017 of the Iowa Agricultural Experiment Station, Project 1139, pp. 370-391. (1951)