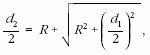
Fizikai Szemle honlap |
Tartalomjegyzék |
Bartos-Elekes István
Ady Endre Líceum, Nagyvárad
A kísérlet mérési eredményeit mindig el kell fogadni! Ha a mérési eredmények nem egyeznek az irodalmi adatokkal, akkor a mérőkészülékben, vagy a mérési módszerben van a hiba. A fizikus ilyenkor megkeresi a hibát. Ha nem találja, akkor vagy nem ért hozzá, vagy egy majdani Nobel-díjas kísérletével állunk szemben...
1997-ben Nagyváradon rendezték meg a romániai Fizikai Olimpia (O.K.T.V) országos döntőjét. Az elektron felfedezése után száz évvel e jubileumi alkalomra, az elektron fajlagos töltése meghatározását és az ehhez tervezett készülékeket ajánlottam a XII. osztályos versenyzők kísérleti próbájára (80 példányban). A készülékek prototípusát már 1971-ben megépítettem, azóta bemutató kísérletként sokszor használtam. A megmaradt készülékek segítségével a verseny után egy egész osztállyal (14 mérőhely) végezzük el a laboratóriumi gyakorlatot.
Az elektron fajlagos töltése meghatározásának igen sok módszere ismert, a legtöbb berendezés a kettős eltérítés elvét alkalmazza együttes elektromos és mágneses terekben. Az elektron által leírt pályából, vagy egy ismert pályára kényszerítés feltételeiből kiszámíthatjuk az e /m-et, a fajlagos töltést. Az itt bemutatásra kerülő kísérletnek abban rejlik az igazi szépsége, hogy látszólag mindent jól mérünk, de a kapott érték mégis, szinte egy nagyságrenddel eltér az irodalmilag elfogadott értéktől. A jövő fizikuspalántáinak, a mérések elvégzésén kívül az a feladata, hogy csak a kísérletek alapján, találják meg a hiba okait. Az iskolai laboratóriumi gyakorlat előtt egy sor részkísérletet is bemutatok, ezek egy része nagyon munkaigényes, illetve nincs elég készülék az egész osztállyal való kísérletezéshez. Itt mindegyik kísérlet bemutatásra kerül, a kapcsolási rajzokkal együtt (talán érdekesnek ígérkezik a középiskolai körülmények között a tized µA-es áramok három számjegyes mérése).
Egy vákuumdiódát elektronforrásként használunk fel, az elektronokat (elvileg) körpályára kényszerítjük. A katódból kissebességű, nem gyorsított elektronok (termikus elektronok) lépnek ki, és ezzel a kilépési sebességgel, vagy az anód gyenge elektromos terében felgyorsulva (gyorsított elektronok) az anód felé tartanak. Az elektronok a transzverzális mágneses térben a Lorentz-erő hatására körívet írnak le, majd az anódba ütköznek; így jön létre az anódáram. A pálya görbületi sugara és a mágneses tér erőssége között egyértelmű kapcsolat van. A mágneses tér növelése esetén a görbületi sugár csökken, majd egy kritikus érték felett az elektronok többé már nem érik el az anódot, az anódáram hirtelen csökken. Az elektroncső fizikai felépítése és méretei alapján meghatározható az anód és a katód közé "beférő" legkisebb körpálya mérete, illetve innen kiszámítható az elektron fajlagos töltése. A nagyfrekvenciás technikában a magnetronok hasonló elven működnek, ezért a fajlagos töltés (e /m) meghatározásának ezt a módját magnetron-módszernek nevezték el.
Az 1. ábrán a dióda belső felépítésének keresztmetszete látható. Az ábra alapján felírható a következő összefüggés:
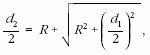
ahonnan megkapjuk az anód elérésének geometriai feltételét:
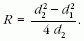
A fizikai feltételt a Lorentz-erő és a centrifugális erő egyensúlyából kapjuk:
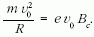
A geometriai és fizikai feltételeket összevetve a
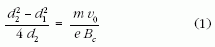
egyenletet kapjuk. Bc a kritikus mágneses indukció értéke, amely az Ia = f (Io) görbe inflexiós pontját jelöli.
 |
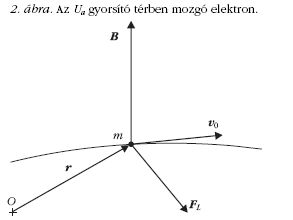 |
A Bc-t az Ic kritikus áram értékéből számíthatjuk ki az induktivitás definíciós képlete alapján:
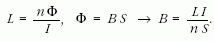
A kritikus értékre alkalmazva a
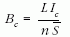
képletet kapjuk, ahol 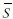 a tekercs átlagkeresztmetszete,
L a tekercs induktivitása, n a tekercs menetszáma.
Az (1) egyenletben elvégezzük a szükséges műveleteket
és megkapjuk az elektron fajlagos töltése abszolút
értékének számítási képletét (a Lorentz-erő skaláris
formában való felírásával elveszítettük az elektron
töltésének előjelét):
a tekercs átlagkeresztmetszete,
L a tekercs induktivitása, n a tekercs menetszáma.
Az (1) egyenletben elvégezzük a szükséges műveleteket
és megkapjuk az elektron fajlagos töltése abszolút
értékének számítási képletét (a Lorentz-erő skaláris
formában való felírásával elveszítettük az elektron
töltésének előjelét):
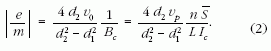
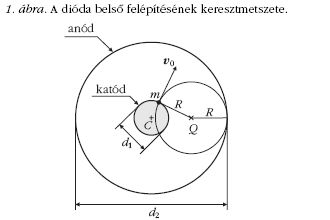
Felírjuk a Lorentz-erő forgatónyomatéka hatására létrejövő pályanyomaték (K) változási sebességét. A tagokat egyenként felírva egy kettős vektorszorzathoz jutunk (2. ábra):
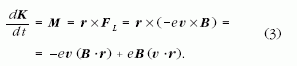
A mágneses indukcióvektor merőleges az elektron mozgási síkjára, így a (3) egyenletben B r = 0, tehát a Lorentz-erő forgatónyomatéka:
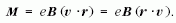
Észrevehető, hogy
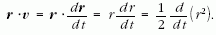
Az eddigieket felhasználva újból felírhatjuk a pálya-nyomaték változási sebessége képletét:
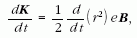
ahonnan
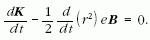
Ezt a kifejezést teljes deriváltként is felírhatjuk:
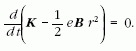
Mivel a derivált értéke zérus, a deriválandó kifejezés értéke állandó:
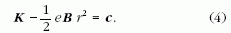
A (4) kifejezés állandó marad a katódból való kilépés- től az anód eléréséig. Indexeljük a kilépési értékeket S-sel (Start), az érkezésieket T-vel (Target). A (4) kifejezés így alakul (a Bc -t állandónak vesszük az egész térben):
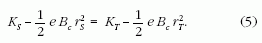
A kezdeti és végső feltételek alapján felírhatjuk: KS = 0 (elhanyagoljuk a termikus elektronok kilépési sebességét), rS = d1/2, rT = d2/2, KT = mvd2/2. Behelyettesítjük az (5) egyenletbe, majd kifejezzük az anódhoz való érkezés sebességét:
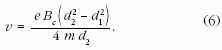
A gyorsító feszültség hatása alatt az elektronok végsebessége a következő képlettel számítható ki:
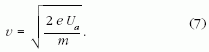
A (6) és (7) kifejezéseket összevetve, a négyzetre emelés után megkapjuk az elektron a fajlagos töltése abszolút értékének számítási képletét (a Lorentz-erő felírásánál már figyelembe vettük az elektron negatív töltését):
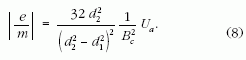
A (8) kifejezésbe behelyettesítjük a kritikus mágneses indukció (Bc) értékét:
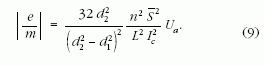
Következtetés: A termikus elektronok esetében a (2), a gyorsított elektronok esetében pedig a (9) képlet segítségével kiszámítható az elektron fajlagos töltése. A következőkben, meghatározhatóvá kell tennünk a (2) és a (9) képlet jobb oldalain szereplő fizikai mennyiségeket.
A fenti megállapítás szerint a (2) képlethez a termikus elektronok legvalószínűbb sebességét (vp ), mindkét képlethez pedig (a mágneses indukció számításához szükséges) a diódát is tartalmazó tekercs-induktivitását (LD) kell meghatároznunk. A többi mennyiség konstrukciós, vagy közvetlenül mérhető adat. A kísérleti berendezés összerakásakor a két képletben "szereplő" fizikai eszközöket olyan módon kell kiválogatnunk, hogy a lehetőségekhez mérten, a lehető legkisebb mérési hibát okozzák.
A magnetron-módszer legfontosabb eleme, egy
könnyen hozzáférhető elektronforrás. Vákuumdiódaként
a valamikori fekete-fehér TV nagyfeszültségű
egyenirányítójában használt elektroncsövet (3. ábra)
választottam ( típusú, ejtsd: 3C18P). A választás
azért esett erre az elektroncsőre, mert a közvetett fűtésű
katódja igen kis átmérőjű, az anódja pedig ehhez
képest jóval nagyobb, így az elméleti számításokban
feltételezett ideális körülményeknek igen jól megfelel
(nagy átmérőjű anód, kis átmérőjű katód). Az sem
hagyható figyelmen kívül, hogy csak ebből tudtam
beszerezni nagyobb mennyiséget. Az elektroncső belsejében
létrehozott magas vákuum (valamikor 20 kV
egyenirányítására tervezték) biztosítja a katód által
kibocsátott elektronok szabad, ütközésmentes mozgását.
A dióda katódja egy vékony cső, anódja a katóddal
koaxiálisan elhelyezett henger. A katódot a belsejében
található izzószál körülbelül 800 °C-ra hevíti
fel. A felhevített katód elektronokat bocsát ki, ezek
maguktól is elérnek az anódig, így néhány tized mA-es
anódáram alakul ki (termikus elektronok). A gyorsított
elektronok esetében, az anód potenciálja a katódhoz
képest pozitív lévén, vonzza ezeket az elektronokat,
megjelenik egy mA nagyságú anódáram.
Felépítés szempontjából az ezüst színű henger az
anód, amely koncentrikus az elektroncső üvegházával,
míg a katód e henger belsejében található és koncentrikus
az anóddal. A cső tetején az anód csatlakozása
van. A fekete folt a gyártáskor az üveg falára
lecsapódott bárium, ez biztosítja a vákuumozáskor
még megmaradt oxigénmolekulák befogását (getter).
típusú, ejtsd: 3C18P). A választás
azért esett erre az elektroncsőre, mert a közvetett fűtésű
katódja igen kis átmérőjű, az anódja pedig ehhez
képest jóval nagyobb, így az elméleti számításokban
feltételezett ideális körülményeknek igen jól megfelel
(nagy átmérőjű anód, kis átmérőjű katód). Az sem
hagyható figyelmen kívül, hogy csak ebből tudtam
beszerezni nagyobb mennyiséget. Az elektroncső belsejében
létrehozott magas vákuum (valamikor 20 kV
egyenirányítására tervezték) biztosítja a katód által
kibocsátott elektronok szabad, ütközésmentes mozgását.
A dióda katódja egy vékony cső, anódja a katóddal
koaxiálisan elhelyezett henger. A katódot a belsejében
található izzószál körülbelül 800 °C-ra hevíti
fel. A felhevített katód elektronokat bocsát ki, ezek
maguktól is elérnek az anódig, így néhány tized mA-es
anódáram alakul ki (termikus elektronok). A gyorsított
elektronok esetében, az anód potenciálja a katódhoz
képest pozitív lévén, vonzza ezeket az elektronokat,
megjelenik egy mA nagyságú anódáram.
Felépítés szempontjából az ezüst színű henger az
anód, amely koncentrikus az elektroncső üvegházával,
míg a katód e henger belsejében található és koncentrikus
az anóddal. A cső tetején az anód csatlakozása
van. A fekete folt a gyártáskor az üveg falára
lecsapódott bárium, ez biztosítja a vákuumozáskor
még megmaradt oxigénmolekulák befogását (getter).
B mágneses indukciójú mágneses tér létrehozására szolgál (4. ábra), és a dióda foglalata körüli fekete gyűrűre kell helyezni, koaxiálisan a diódával. A tekercset az elektronikus stabilizáló áramkör táplálja.
 |
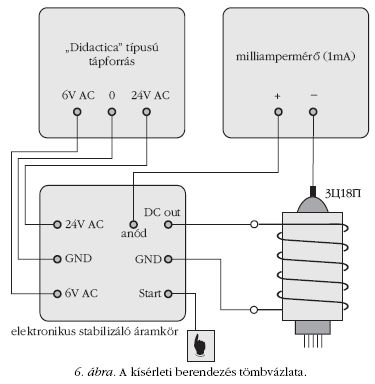 |
A kísérleti berendezés tömbvázlata a 6. ábrán látható. A vákuumdióda egy áramjárta tekercsben található. Egy elektronikus stabilizáló áramkör segítségével rövid ideig (10 s) igen erős és kiszámítható értékű mágneses teret (pontosabban, mágneses indukciót) hozhatunk létre. Az időkorlátozás a tekercs esetleges túlmelegedése miatt szükséges. Ez az áramkör adja a stabilizált anódfeszültséget is, a gyenge elektromos gyorsítótér létrehozásához, valamint itt található a vákuumdióda fűtéséhez szükséges áramkör. Az elektronikus stabilizátor egy klasszikus, iskolai, "Didactica" típusú tápforrásról működik. Az elektroncső anódáramát a milliampermérő, egyedi méréseknél digitális mikroampermérő segítségével mérjük meg.
Ezek az adatok feltétlenül szükségesek a mérési eredmények feldolgozásához.
 típusú vákuumdióda:
típusú vákuumdióda:
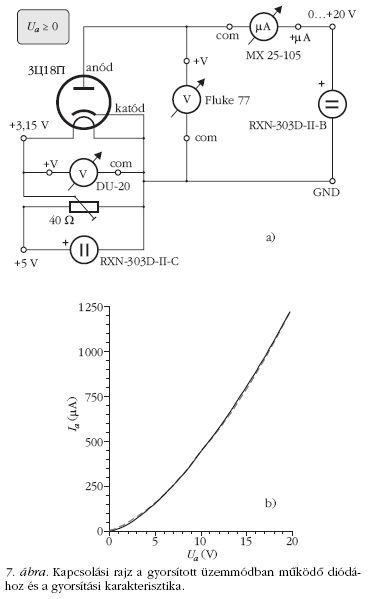
A 7.a ábrán látható kapcsolás segítségével felvettük a dióda voltamperes karakterisztikáját (7.b ábra). Az anódáramot egy egyszerű digitális mikroampermérővel mérjük.
 |
 |
A mérési eredmények az 1. táblázatban
láthatók. A mérési sor adatai a gyorsítási anódkarakterisztikát
írják le. A 7.b ábrán szereplő szürke, szaggatott
grafikonból jól láthatjuk, hogy érvényesül az 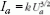 formájú, az irodalomból ismert háromkettedes
törvény. A későbbiekben használt Ua = 19,5 V gyorsítási
feszültség kisebb az itt alkalmazott 19,8 V-nál, és
az anódáram görbéje egyáltalán nem mutatja jelét a
telítődésnek, vagyis az elektronok sebességét a gyorsításukra
felhasznált munka alapján számíthatjuk ki:
formájú, az irodalomból ismert háromkettedes
törvény. A későbbiekben használt Ua = 19,5 V gyorsítási
feszültség kisebb az itt alkalmazott 19,8 V-nál, és
az anódáram görbéje egyáltalán nem mutatja jelét a
telítődésnek, vagyis az elektronok sebességét a gyorsításukra
felhasznált munka alapján számíthatjuk ki:
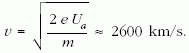
Következtetés: ez a dióda a gyorsítási üzemmódban megfelelő elektronforrásnak tűnik a fajlagos töltés meghatározására.
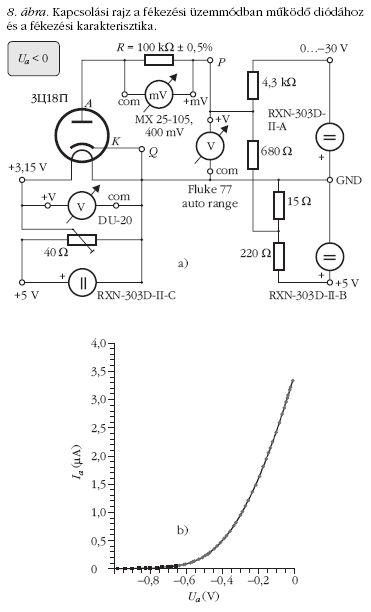
Az előbb Ua = 0 V-nál egy igen kis értékű anódáramot figyelhettünk meg. Az áram létrejöttének tisztázására az anódfeszültséget negatív irányba is eltoltuk. A fékezési üzemmódban a 8.a ábrán látható kapcsolást használtuk. Az UPQ anódfeszültség-forrás folytonosan szabályozható feszültséget ad a 0-1000 mV feszültségintervallumban. A kapcsolás érdekessége, hogy a szabályozott tartományt a felső táp feszültségének beállításával érjük el. A másik érdekesség, hogy a rendkívül kicsi, néhány tized µA-es anódáramokat egy precíziós ellenálláson (R = 100 kΩ ± 0,5%) létrejövő feszültségből számítjuk vissza, miközben természetesen az anódfeszültséget is korrigálni kell. A mért UR (mV) értéket le kell vonnunk az UPQ -ból: UAK = UPQ-UR. Az anódáram értékét a következő összefüggésből számíthatjuk ki: Ia (µA) = UR (mV) / (100 kΩ). A mérési eredményekből (8.b ábra) látható, hogy a negatív anódfeszültség a termikus elektronok lefékezésére szolgált. A grafikon, de inkább a 2. táblázat adataiból meglepődve vesszük észre, hogy az elektronok gyorsítás nélkül is eljutnak az anódig, ezeket az elektronokat termikus elektronoknak nevezzük. Az egyre nagyobb fékezőfeszültséggel megállítjuk a katódból kilépő elektronokat, így meghatározható a termikus elektronok legnagyobb, valamint legvalószínűbb sebessége. A legnagyobb sebességnek a kísérlet szempontjából csak információs jelentősége van, a legvalószínűbb sebesség azonban a termikus elektronok által leírt legvalószínűbb körpálya adatainak kiszámításához nyújt majd segítséget. A 8.b ábra a dióda fékezési karakterisztikája. Látható, hogy a leggyorsabb elektronokat is le tudjuk fékezni az 1000 mV-os fékezőfeszültséggel. Innen kiszámítható a termikus elektronok legnagyobb sebessége:
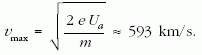
A legkisebb négyzetek elve segítségével a mérési pontokra egy negyedfokú polinom függvényt illesztünk. A függvény elsőrendű deriváltja, egy bizonyos fékezési feszültségnél, a feszültség megváltoztatásakor létrejövő áramváltozás mértékét adja meg µA/Vban.
Ez az áramváltozás a nulla anódfeszültségnél a legnagyobb (legmeredekebb a görbe), itt a nagyon kicsi sebességű elektronokat fékezzük le. A második derivált az áramváltozás változási sebességét írja le µA/V2-ben. Segítségével megkapjuk az eredeti, negyedfokú görbe inflexiós pontját, ahol a legtöbb elektront vonjuk ki a "forgalomból". Az inflexiósponti fékezőfeszültségből számíthatjuk ki a legvalószínűbb sebességet, mert ilyen sebességű elektronból van a legtöbb. A második derivált (ez egy másodfokú függvény) maximumhelye megadja az inflexiósponti legvalószínűbb sebességű elektronokhoz tartozó fékezőfeszültséget. Ez a feszültség a másodfokú illesztési görbe egyenletéből, vagy egyszerűen, a grafikonból is megkapható: Up = -0,263 V. A termikus elektronok legvalószínűbb sebessége (vp):
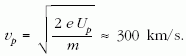
Ez várható érték volt, hiszen ennek valahol a sebesség eloszlási görbe szimmetria-középpontjában kell lennie. A legvalószínűbb sebességet egyszerűbb, de kevésbé pontos módon is megkaphatjuk. "Kézzel" deriváljuk a dióda fékezési karakterisztikáját, rendre, félvoltonként megmérjük az érintő iránytényezőjét, és azonnal µA/V egységekben fejezzük ki (tengelymetszetes alak). A 9. ábra grafikonján jól látható az inflexiós pont, illetve a hozzátartozó Up fékezőfeszültség. A módszer előnye, hogy számítógép, sőt felső matematikai ismeretek nélkül is megrajzolható, megérthető.
Következtetés: ez a dióda a fékezési üzemmódban is megfelelő elektronforrásnak tűnik a fajlagos töltés meghatározására.
A rendelkezésre álló tekercs nem szolenoid, tehát induktivitását kísérletileg kell meghatároznunk. A kondenzátordekádunk segítségével (C = 0,5 µF állásban) egy soros RLC-áramkört hozunk létre és a TR0163 típusú hangfrekvenciás generátorral tápláljuk (10. ábra). Az R ellenállás a tekercs saját ellenállása. A jel nagyságát állandó értéken tartva (U = 3 V) változtatjuk a frekvenciát, és mérjük a kondenzátoron levő feszültséget. A 3. táblázatban láthatjuk az üres tekerccsel (3.a táblázat) és a tekercsbe helyezett diódával (3.b táblázat) mért adatokat. Ezekből, de leginkább a belőlük megrajzolt grafikonokból (11.a és 11.b ábra) más, a mágneses tér keltésével kapcsolatos igen fontos dolgokat is meghatározhatunk.
A tekercs segítségével állítjuk elő azt a transzverzális mágneses teret, amelyben az elektronok körpályára kényszeríthetők. A tér értékének kiszámíthatósága és a homogenitása az elsőrendű követelmény az e /m meghatározás pontossága szempontjából.
A kísérletből egyértelműen látható, hogy a rezonanciafrekvencia erősen csökken, ha a dióda a tekercsben van, ez ferromágneses anyagok jelenlétére utal. Az is látható, hogy a második esetben a rezonanciagörbe maximuma szinte felére csökken, a sávszélesség nő, ez Foucault-áramok által okozott komoly veszteségekre utal, vagyis a ferromágneses anyagok az elektroncső szerkezetéhez tartozó nagyobb acéldarabok lehetnek. A Thomson-képlet segítségével kiszámíthatjuk a tekercs L induktivitását:
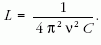
Az üres tekercsre L = 42,5 mH, a diódás tekercsre pedig LD = 66,2 mH értéket kapunk. A rendelkezésre álló áramforrás által adható legnagyobb feszültség (25 V) és a tekercs 27 Ω-os ellenállása meghatározza a legnagyobb áramot: Imax = 0,93 A. A tekercs átlagkeresztmetszete:
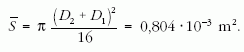
Kiszámíthatjuk az üres tekerccsel elérhető legnagyobb mágneses indukciót:
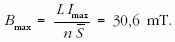
Figyelembe véve a gyorsított elektron elérhető legnagyobb sebességét, kiszámítható a tekercs által létrehozható legkisebb körpálya átmérője:
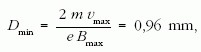
ami bőven "belefér" a katód és az anód közötti térbe, tehát a tekercs alkalmas a fajlagos töltés meghatározásához szükséges mágneses térerősség keltésére. Fentebb azt is láttuk, hogy a diódában ferromágneses anyagok vannak, ezek az elektroncső belső szerkezeti elemei, az anód és a katód nikkelt is tartalmazó
alkatrészei. A keltett tér átlagértéke csak LD /L = 1,56-szor nagyobb a ferromágneses anyagok nélkül mérhető értéknél, de egyes helyeken, a ferromágneses anyagok közelében, ez az érték száznál is nagyobb lehet. Rendkívül erős pályamódosításokra számíthatunk, a körpálya ebben az esetben csak papíron létezik.
A négy előkészítő kísérletből levonható következtetések:
Tanulmányoztuk az Ia (µA) anódáram változását a tekercsen átfolyó I0 (mA) áram függvényében. A gyorsítási feszültséget Ua = 19,5 V-ra állítottuk. A kísérleti adatokat a 4. táblázat b) részében foglaltuk össze.
Az Ia anódáramot ábrázoljuk a mágneses teret létrehozó, a tekercsen átfolyó I0 áram függvényében. A termikus elektronok esetében látható, hogy a mágneses tér egy bizonyos értékéig az anódáram lényegében nem változik, majd erőteljesen csökkenni kezd. A mérések összekötése a legkisebb négyzetek elve alapján történik két szakaszban, mivel nem található olyan polinom, amely megfelelne az ilyen típusú méréseknek (12.a ábra). A nagyobb I0 értékeknél jól látható a hatodfokú függvény "oszcillációja" a kevés és szétszórt mérési pont miatt. A kritikus pontra kapott letörési áram értéke: IcT = 180 mA (criticThermic). A gyorsított elektronok (12.b ábra) esetében is megfigyelhető, hogy a mágneses tér kis értékeinél az anódáramot nem befolyásolja mágneses tér jelenléte, de a letörési érték jóval nagyobb az előbbinél, IcA = 360 mA (criticAccelerated). Az előbbi kísérlethez képest egy másik különbség is adódik: a letörési szakasz meredeksége kisebb, és egy "maradék" anódáram is van. A mérési pontok jobb összetartása miatt az összekötésüket sikerült jobban megoldani, de itt is, csak két szakaszban, szintén magas fokú (hatodfokú) polinomok segítségével.
A katód által kibocsátott elektronok transzverzális mágneses térben mozognak. A reájuk ható Lorentz-erő hatására körívet írnak le, amelynek görbületi sugara a transzverzális mágneses tér erősségétől függ. Minél nagyobb a mágneses tér indukciója, annál kisebb a görbületi sugár. Egy bizonyos érték után az elektronok nem érik el az anódot, és az anódáram hirtelen csökken. A kritikus érték a gyorsító feszültségtől, valamint az elektroncső mechanikai felépítésétől függ. A görbék meredekségében látható lényeges különbséget a vízszintes nagyításnak tulajdoníthatjuk. A tér erős inhomogenitásának következménye, hogy a transzverzális komponens nagysága a széleken nem elég a nagy sebességű elektronok pályájának "begörbítésére", látszólag ezen elektronokra a mágneses tér nem hat.
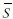 értéke a konstrukciós adatokból
értéke a konstrukciós adatokból
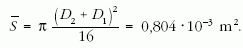
A mágneses indukció számításához a ferromágneses
anyagot is tartalmazó tekercs induktivitását (LD) használjuk.
A termikus elektronokra a megadott, vagy
kiszámított értékek alapján (d1 = 0,9 mm, d2 = 9,8 mm,
vp = 300 · 103 m/s,
IcT = 180 mA, L = LD = 66,2 mH,
n = 1600, 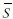 = 0,804 · 10-3
m2) a (2) egyenletből következő
értéket kapjuk:
= 0,804 · 10-3
m2) a (2) egyenletből következő
értéket kapjuk:
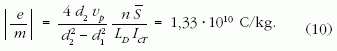
A gyorsított elektronokra a megadott, vagy kiszámított
értékek alapján (d1 = 0,9 mm,
d2 = 9,8 mm,
Ua = 19,5 V, IcA = 360 mA,
L = LD = 66,2 mH, n = 1600,
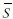 = 0,804 · 10-3 m2)
a (9) egyenletből következőt kapjuk:
= 0,804 · 10-3 m2)
a (9) egyenletből következőt kapjuk:
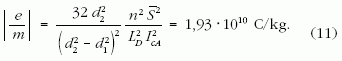
A bemutatott módszer segítségével meghatározható az elektron fajlagos töltése. A kísérlet során az irodalmilag elfogadott 1,759 · 1011 C/kg értéknél szinte egy nagyságrenddel kisebb értéket kaptunk az elektron fajlagos töltésére, ami komoly konstrukciós hibákra utal. A kísérleti fizikus ilyenkor megkeresi készüléke hibáit, hogy újabb berendezése segítségével pontosabb eredményeket kapjon, majd újabb készüléket épít, majd megint újat...
E laboratóriumi gyakorlatnak épp ez volt az érdekessége: megtalálni a mérési hibák okát, okait! A főbb hibaforrásokat a következőkben tudjuk összefoglalni: