KÖZÉPISKOLAI DEMONSTRÁCIÓS KÍSÉRLETEK ELEMZÉSE

Wiedemann László
Budapest

A görög filozófiai felfogás szerint az axiomatikus gondolkodás és annak eredményei bírnak csupán igazságtartalommal. Az empíriával szemben arisztokratikus módon elzárkóztak, szinte lenézték azt.

A megismerés folyamata az újkorban épül tovább, és kellő filozófiai súlyt kap Bacon és Hume munkássága által, amikor az empíria is a megismerés hiteles módszerévé, hiteles eszközzé válik. Az empíria anyaga adja az axiomatikus gondolkodás tartópilléreit és frissíti az axiómákat, ahogy ezt manapság elképzeljük. Galileinél tetőzik ez a kettősség a módszeresen végigvitt kísérletezésben és elméletalkotásban. Ezáltal bővülnek a természettudományban az igazságkritériumok. Megfigyelés és kísérlet az egyik oldalon, elméletalkotás a másik oldalon.

Fizikatörténeti előadásaiban Simonyi Károly professzor mindig nyomatékkal emelte ki a kísérletezés fontosságát; úgy mondta gyakran, hogy "Galilei vett egy lejtőt", vagyis nemcsak elképzelte, vagy az ideáját tekintette, hanem kézbevette és méréseket végzett vele.

A sorra kerülő kísérletek nem kutatás célúak, hanem igazoló, illetve a törvény érvényességét alátámasztó kísérletek. A tanításban főleg ilyenek szerepelnek, de előfordulnak fizikai mérések, mérő-kísérletek is. Itt sohasem felfedezésről van szó, hanem vezetésről. Naivitás felfedezésként aposztrofálni az iskolai fizikai méréseket. Inkább utánérzésről van szó, jelentős kutatók eljárásait ismételjük meg célirányos módszertani egyszerűsítésben.

Empíria és kísérlet előzetes, vonatkozó elméleti ismeretek nélkül semmit sem ér. A dolog értelméhez kell eljutni. Ezt nem nyerhetjük a látványosság szépségével vagy egyszerű manipulációval. A látottak mögé kell nézni, távolabbi szintetizálás, vagyis valamilyen szemléletalkotás érdekében. A kísérleti eredményeket kell beilleszteni már ismert elméleti rendszerbe. Amikor ez nem megy, ott állunk a nagy felfedezések küszöbén.

A kísérletek ilyen értelmezése sorrendet jelöl ki. Az előbbiek szerint elsőként a kísérlet mélyebb értelmezése, ezután viszont visszatérés az alapszituációra, de más oldalról való közelítéssel. Ezáltal megvalósul a tapasztalat és elmélet erősebb összekapcsolása. Mindezt a matematika fokozott bevonásával tesszük. A kísérlet és elmélet egységében egy új igazságkritérium jelenik meg. Sok esetben az elemzések differenciálegyenletek alkalmazását is szükségessé teszik. Ilyenkor mindig tanári szintre kell gondolni, de kellő módszertani tudással vissza lehet térni egyszerűbb magyarázatra is.

Ellenpontként itt belép egy ismert didaktikai aggály. Vannak, akik az egyszerűség bűvöletében élnek, e vélemény a naivitásig mehet. Mondják, a természet olyan egyszerű és világos, csak követni kell. A kísérletek és a magyarázatok is legyenek egyszerűek, minden más túlbonyolítás. Úgy gondolják, ha a látvány szórakoztató, már érthető is a kísérlet. Lebilincselni ajánlatos, de nem elegendő. Hasonló ez a feleletválasztós kérdések attrakcióihoz; felszínességet hordoz a konstrukciójuk, ezt preferálják, holott valójában a kérdések jók és tartalmasak.

Tehát vigyázzunk a túlzott analizálással, de a túlzott egyszerűsítéssel is. Härtlein Károly barátom (BME Fizikai Intézet) gyakorta szokta emlegetni beszélgetéseinkben Einstein egyik ominózus kitételét, amely szerint "egyszerűsítsük le a tudományos magyarázatokat, amennyire lehet, de annál jobban semmiképpen".

Lássunk néhány példát a problémakezelés egymásra épülő szintjeire.

Vasmag leemelése-leszakítása áramjárta tekercsről

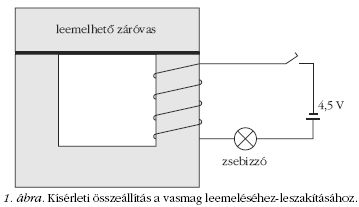
Az iskolai demonstrációs transzformátorkészletből veszünk egy tekercset (1200 menetes), ezt ráhúzzuk a vasmagra és zárt vasmagot hozunk létre. Ezután egyszerű egyenáramú áramkört létesítünk 4,5 voltos teleppel a tekercs és egy zsebizzó sorba kötésével (1. ábra). A kísérlet most annyi, hogy a vasmag felső részét (elég nagy erővel) leszakítjuk az alsóról. Eközben azt látjuk, hogy az izzó erőteljesen felvillan, majd ismét visszanyeri eredeti fényerejét. De még ki is éghet. Ha a vasmag leszakított részét, a felső leemelt részt ráejtjük az alsó részre - így ismét zárt vasmagunk lesz -, a ráesés rövid időtartamára az izzó fénye teljesen elhalványodik, majd rövidesen ismét visszanyeri eredeti fényerejét. A kísérlet látványos, a magyarázat az elektromágneses indukció nem szokványos megjelenésére utal, amikor egy mágneses kör mágneses ellenállása változik. Az értelmezés, egyre mélyebben, három lépcsőben lehetséges.

Kvalitatív magyarázat. A leszakítás ideje alatt az izzón átfolyó áram megnő, mivel fényereje nagyobb lett. Ez csak úgy lehetséges, hogy fellépett egy beiktatott ellenfeszültség. Ez éppen a körben keletkezett indukált feszültség, ami fluxusváltozás eredménye. Úgy vehetjük, hogy leemeléskor zárt vasmag helyett légréssel bíró vasmagos tekercsünk lesz. Minthogy a B-tér forrásmentes (divB = 0), és a B-vonalak merőlegesek a vas-levegő elválasztó felületre, a légréssel bíró mágneses körben mindenhol ugyanannyi és könnyen kiszámítható B-vonal halad. Ezen B-vonalak száma a légrés miatt most jóval kevesebb, mint zárt vasmag esetén, tehát a (BA) fluxus csökkent, így a vasmagot körbefogó tekercsben indukált feszültség keletkezik a leemelés ideje alatt, amely az áramkörben a telepfeszültséghez előjelesen hozzáadódik. A Lenz-törvény következtében viszont az indukált feszültség a fluxus csökkenését akarja akadályozni, az eredeti fluxust akarja fenntartani, tehát a kör összes feszültségét növeli, ezáltal növeli a kör áramát, hogy az eredeti fluxus kevésbé csökkenjen. Ezért az indukált feszültség növeli a kör összes feszültségét.

A vasmag ráejtésekor éppen a fordított zajlik; itt az indukált feszültség a már kisebb fluxust akarja fenntartani, így most a telepfeszültséggel ellentétes, aminek következtében kevesebb áram folyik a körben, mint az eredeti teljes fluxus esetén.

A kísérleti elrendezést egy x vastagságú légréssel ellátott toroid tekerccsel modellezhetjük. Írjuk fel a gerjesztési törvényt a körre, amikor figyelembe vesszük, hogy B = µH, ahol µ =µ₀µ_r. Ezzel egyúttal kijelöltük az egyszerűsítés egy körét, amennyiben a hiszterézisgörbe helyett B és H között lineáris kapcsolatot tételezünk fel.

Kihasználjuk, hogy a mágneses körben B mindenhol ugyanaz, mivel a B-tér forrásmentes, továbbá B-nek normál komponense a vas-levegő elválasztó felületen maga a teljes B-érték. A számítás vonalintegrál helyett most szorzatösszegre redukálódik:

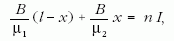
ahol az első tagban a vas permeabilitása szerepel, a második tagban a levegőé, továbbá l a toroid középvonalának hossza, n a tekercs menetszáma, I a kör áramerőssége. Mivel a vas relatív permeabilitása ~ 5000, a levegőé viszont 1, ezért jó közelítéssel az A keresztmetszetű vasmag fluxusa

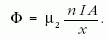
A légrés növelésével a fluxus láthatóan csökken. Ennél a közelítésnél a hiszterézisgörbét kiiktattuk, mivel ezáltal a jelenséget meghatározó hatás a légrésre koncentrálódik.

Az előbbi leírás ugyan már kvantitatív, de csak közelítő jellegű, ugyanis x növelésével maga a gerjesztő I áram is változik, így I magának x-nek is függvénye. A további számoláshoz x változását elő kell írnunk, például állandó sebességgel emeljük le a vasmagot. Ez a legegyszerűbb eset: x = v t, v a leemelés sebessége, t az idő. Ha most így az x(t) függvényt ismerjük, akkor a körre felírt huroktörvény segítségével ez a bonyolult folyamat differenciálegyenlettel leírható:

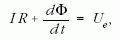
ahol R a kör teljes ohmos ellenállása, a jobb oldal a telepfeszültség és Φ deriváltját az első képletből kell előállítani oly módon, hogy az áramot is az idő függvényének tekintjük. Tehát ezt a deriváltat törtfüggvény deriváltjaként kell előállítani. Ezáltal I (t)-re differenciálegyenletet kapunk. A részletek megtalálhatók a szerző egyik cikkében: Fizikai Szemle 1970/3. szám. Ezúttal tájékozódásképpen egyszerűbb közelítést veszünk. Mivel a légrés vastagsága kicsi, és állandó sebességgel mozgatjuk a vasmagot, azért vegyük most x átlagát, ami egy állandó érték és ezt a törtfüggvény idő szerinti deriváláskor a végén vesszük figyelembe:

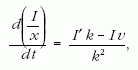
ahol k jelenti x átlagát, vagyis a résszélesség felét és v a már mondott mozgatási sebesség. Ezt a fenti huroktörvénybe helyettesítve kapunk egy elsőrendű, inhomogén differenciálegyenletet az I (t) függvényre: aI'+bI = U_e, ahol a és b állandók. b = R-λv, λ szintén állandó. Az áramerősségre a partikuláris megoldás

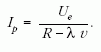
Ha az eredeti, légrés nélküli állapotban számolnánk az áramerősséget, Ohm törvénye alapján

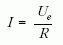
értéket kapnánk. Világosan látszik, hogy az előbbi áram - mikor a vasmagot leszakítjuk - nagyobb mint a stacionárius áram, és pedig nagyobb szakítási sebesség esetén nagyobb lesz.

Felfüggesztett rugó anyageloszlása

Nagy átmérőjű (~ 10 cm), sűrű menetű, laza spirálrugót (slimky) egyik végénél fogva felemelünk és nyugalomban tartjuk. Függőlegesen lóg, a másik vége szabad. Az egyes menetek távolsága mérvadó a helyi anyageloszlásra (2. ábra). Azt tapasztaljuk, hogy a menetek egymás közti távolsága a felfüggesztés közelében a legnagyobb. Úgy mondhatnánk, hogy ez a spirálrugó-alakzat a felfüggesztés körül a legritkább. Nem a rugó anyagának a sűrűségéről van szó! Határozzuk meg számolással és méréssel ebben az állapotában anyageloszlását. Hasznos lehet a vonalsűrűség fogalmának bevezetése. A ρ vonalsűrűségen az egységnyi hosszúságra eső tömeget értjük.

A középiskolai gyakorlatban, ha a Hooke-törvény előfordul, akkor azt többnyire a szál végére írjuk fel. E problémában általánosítva felhasználjuk, hogy a Hooke-törvény a rugalmas szál belső pontjaira is érvényes, egyben differenciális formában is. A spirálrugó- alakzatot egészében rugalmas szálnak tekintjük. A differenciális Hooke-törvény alkalmazásakor határátmenettel a vonalsűrűség helyfüggése meghatározható: ρ = ρ(x), ahol x a megnyúlt szál mellett képzelt nyújtatlan szálon - az úgynevezett referenciaszál - a befogástól számított távolság. A 2. ábra alapján okoskodunk, de először általánosságban, vagyis a szálat nem feltétlenül gravitációs erő terheli. Hasson F erő a szál végére a szál egyenesében! Vizsgáljuk a belső pontok elmozdulásait a referenciaszálhoz képest! Legyen P₁ pont x₁ távolságra a befogástól, P₂ legyen x₂-re a referenciaszálon mérve! Az F erő hatására P₁ eltolódik és az x₁ szakasz megnyúlása y₁, az x₂ szakaszé y₂, így a Δx szakasz átmegy Δx'-be. Mennyi ez?

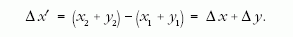
Az y érték a helyi megnyúlás, Δy a Δx hosszúságú szakasz megnyúlása, ahogy a referenciaszálon előre haladunk. Mi a kapcsolat ρ és y között? Ez abból az észrevételből adódik, hogy bárhol is tekintünk egy Δx darabot a referenciaszálon, a benne foglalt tömeg ugyanaz, mint a valódi, vagyis a megnyúlt szálon található Δx'-ben. Ezért az m = ρl definíciós képlettel, ρΔx'= ρ₀Δx, ahol ρ₀ a nyújtatlan szál vonalsűrűsége, ρ a nyújtott szálé. Δx' értékét helyettesítve, ρ-ra kapjuk, hogy

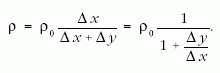
Végül határátmenettel azt kapjuk, hogy

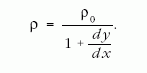
Ez eddig általánosságban igaz. Ha tehát ismerjük az y helyi megnyúlás x-függését, a megnyúlt szál ρ(x) anyageloszlása meghatározható.

A jelen esetben y(x) meghatározása most már azon alapul, hogy a Hooke-törvényt a szál belső pontjaira írjuk fel. A Hooke-törvényben F(x) a szál egyik belső pontjában fellépő erőt jelenti. Alkalmazzuk ρ(x) képletét a felfüggesztett szálra! A referenciaszál P pontjában a húzóerő a P alatti szálrész súlya. Tekintsük ezután a Δx hosszúságú, A keresztemetszetű szakasz megnyúlását! Erre írjuk fel a Hooke-törvényt:

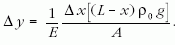
Ezután képezzük a Δy /Δx hányadost, majd határértékre térünk és ezzel az y helyi megnyúlásra kapunk egy differenciális formulát:

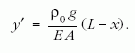
Az egész szálra vonatkozó Hooke-törvényből számolható, hogy EA = DL, ahol D az egész szál direkciós ereje, L a referenciaszál hossza. Így

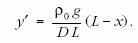
Ha ezt behelyettesítjük ρ fenti általános képletébe, megkapjuk a megnyúlt szál keresett anyageloszlását:

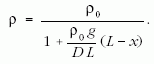
Látható, ha x = 0, vagyis a felfüggesztésnél ρ a legkisebb, míg x = L -nél ρ a legnagyobb, éppen ρ₀. Így ρ(x) megadja a rugalmas szál anyageloszlását.

Meghatározhatjuk a szál teljes megnyúlását is. Mivel dy a dx szakasz megnyúlása, azért a szál teljes megnyúlása

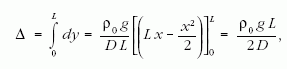
vagy

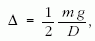
ahol m a szál tömege. A képletnek szemléletes jelentése van: mintha D direkciós erejű súlytalan rugalmas szálra m tömegű testet függesztenénk, ekkor Δ jelenti az itteni megnyúlás felét.

A mérést itt úgy végezzük, hogy a nyújtott szálon egyenlő szakaszokat tekintve, feljegyezzük, hogy hány menet esik egy-egy szakaszra. A menetek száma közelítően követi a sűrűségre adott anyageloszlást.

Léggömb felfúvódása evakuált térben

Kis lufit veszünk - ne fújjuk fel -, jól lekötjük, és helyezzük el lazán az iskolai demonstrációs légszivattyú üvegharangja alá. Ezután kezdjük a leszívást. A lufi kigömbölyödik, dagad, nagyra nő, akár szét is pukkanhat (3. ábra). Vizsgáljuk a lufi sugarát az evakuált tér nyomásának függvényében, és igyekszünk feltételt találni arra, hogy még éppen ne pukkadjon szét.

A jelenséget lényegében a lufi anyagának E rugalmassági modulusza és a nyomáskülönbség határozza meg. Mint érdekesség említhető, hogy leszívás közben az evakuált tér p_k nyomásának csökkenésével a lufi belsejének p_b nyomása is csökken, holott első pillanatra azt várnánk, hogy nagyobb nyomás feszíti.

Két formulát használunk fel: a műszaki mechanikából ismert úgynevezett kazánformulát és a differenciális Hooke-törvényt. Az első esetben, ha a kazán terében p_b nyomás uralkodik, a kazán falában σ feszültség ébred. Hengeres vagy gömb alakú kazánnál egy kettes faktortól eltekintve a képletek azonosak. A kazánformula:

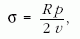
ahol R a gömb (lufi) sugara, v a falvastagság, amit ezúttal állandónak veszünk - egyébként még a Poisson-számot is figyelembe kellene vennünk. Végül p a gömbbeli - értelemszerűen a p_k-hoz viszonyított - nyomást, vagyis a relatív nyomást jelenti: p_b-p_k. Jogos még azt feltételezni, hogy a lufiban lévő levegő izotermikusan tágul. Mindezekből adódik egy egyenletrendszer:

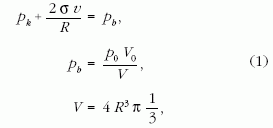
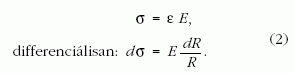
Az utolsó képlethez részletesebb megjegyzés kívánkozik.

Tekintsünk egy analóg helyzetet. Rugalmas szálat nyújt a végén ható F erő. Tetszőleges x helyen az y megnyúlás

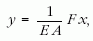
ha F minden x helyen ugyanaz. Ekkor ε = y /x, tehát a relatív megnyúlás is mindenhol ugyanaz. Ha viszont az F erő x-nek függvénye, például ha az egyik végénél fogva felakasztjuk a szálat, akkor y már integrállal számítandó, mint az előző fejezetben. Az y /x hányados így sem adja a helyi relatív megnyúlást, mert y a teljes x szakasz megnyúlásának függvénye, függ x-től. Ugyanígy, ha jelenleg a gömbre

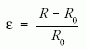
képletet vennénk (R₀ a kezdő sugár), nem a helyi ε-értéket kapnánk. Tehát mindig az aktuális R helyen kell a relatív megnyúlást számítani:

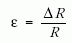
a helyes. Hasonlóan az előbbiekben is adott Δx szakasznak vettük a Δy megnyúlását és így ott

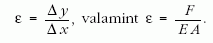
Ha F állandó, ε független a helytől, de x-től függő F esetén

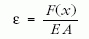
lesz. Valójában a differencia- és a differenciálhányados fizikailag értelmezett különbségéről van szó. Visszatérve az (1) alapegyenletre, amikor e jelenségben a σ feszültséget a Hooke-törvényből vesszük: σ = εE, az úgy lesz helyes, ha ε-ra való tekintettel infinitezimálisan írjuk fel tetszőleges R helyen és ε-ban R-hez viszonyítunk. Tehát

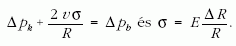
Határátmenetben, felhasználva egy függvény differenciáljának felírását, a megoldandó egyenlet végül a következő lesz:

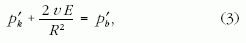
ahol a vessző R szerinti deriváltat jelent. A jobb oldali derivált p_b képletéből nyerhető. A már mondottak szerint

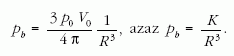
(3)-ból a p_k(R) függvény egyszerűen kiintegrálható:

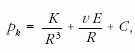
ahol a C állandó a kezdeti feltételekből határozható meg; R = R₀, p_k = p₀ = p_b. A keresett p_k függvény, ami a probléma megoldása, így szól:

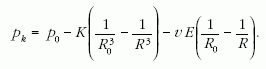
R₀ a sugár kezdő értéke és R > R₀, R növekedtével p_k egyértelműen csökken. Fizikailag az inverz függvény bír szemléletes jelentéssel: a leszívással, vagyis p_k csökkentésével a luftballon sugara növekszik.

A háztartási hűtőszekrény energiaviszonyai

A hűtőszekrény működését kell szemügyre venni és a stacionárius állapotot. A hűtő működését a szakirodalom szerint a fordított, reverzibilis Carnot-körfolyamattal modellezzük. Ennek lényege, hogy energiaközlés árán az alacsonyabb hőmérsékletű hőtartályból hőt juttathatunk a magasabb hőmérsékletű hőtartályba. Spontán ez lehetetlen, tiltja a hőtan második főtétele.

Tekintsük a hűtő belső, hűtendő terét. A hűtőszekrényben lévő szerkezet ciklusonként Q₂ hőt vesz ki a hűtött térből és W munka árán Q₁ > Q₂ hőt ad le a környezetnek. A mechanikai szerkezet, amely a Carnot-ciklust fenntartja, például egy villanymotor által működtetett kompresszor, amely zárt térben cseppfolyósít és elpárologtat valamilyen freont helyettesítő gázt. Így a Carnot-ciklust végző anyag a gáz, a befektetett W munka a motor által végzett munka. A környezet most az a helyiség, ahol a hűtő áll. (Ne vegyük számításba, hogy a helyiség - például konyha - a falán keresztül termikus kapcsolatban van a T_k állandó hőmérsékletű külső környezettel.) Továbbá vegyük figyelembe, hogy a hűtő hőcserélő bordái annak hátsó falán vannak felszerelve, vagyis a Q₁ hő - a 4. ábra szerint az 1-es jelű térnek - a helyiségnek adódik le. Az ismert termodinamikai számítások szerint a ciklusonként végzendő mechanikai munka: W = Q₁-Q₂, a hűtés jósági tényezője η = Q₂/W. Előírhatjuk a hűtés két jellemző hőmérsékletét. Legyen az egyes tér állandó hőmérséklete T₁, a kettes téré az állandó T₂. Ez utóbbit akarjuk fenntartani, a stacionárius állapotot itt kell majd kifejezésre juttatni. Szintén a számítások szerint η kifejezhető az előbbi jellegzetes hőmérsékletekkel:

A hűtő fala nem tökéletesen hőszigetelt, így az egyes térből, valamelyes hő a Carnot-ciklustól függetlenül a hűtött térbe visszaáramlik. Stacionárius állapot akkor uralkodik a kettes, vagyis a hűtött térben, amikor ciklusonként az abból kivett Q₂ hő a hűtő falán át az egyes térből oda visszaáramlik, miközben az egyes tér Q₁ hőt kap. Mindebből az is látszik, hogy Q₁-Q₂ hő fűti az egyes teret, vagyis éppen a befektetett W mechanikai munka. Ha Q₂ nem áramolna vissza ciklusonként, akkor a hűtött tér hőmérséklete állandóan csökkenne. Ez a visszaáramló hő Newton hőátadási törvényéből számolható:

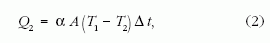
ahol α a hűtő falának hőátbocsátási tényezője, A a hőátadó összes felület, Δt egy ciklus ideje. T₁ és T₂ állandóságát biztosítani kell.

A továbbiak kedvéért fontos megjegyzést kell tennünk. Hangsúlyoztuk, hogy a T₁ hőmérsékletet elő kell írni. De ez azt jelenti, hogy fenn kell tartani. Például télen a helyiséget külön fűtjük, így állítva elő az egyes tér állandó hőmérsékletét. Ezt Newton lehűlési törvénye alapján kiszámolhatjuk. Legyen a fűtőtest, vagy kályha teljesítménye P és a külső környezet állandó hőmérséklete T_k, akkor stacionárius állapotban a helyiség által felvett és leadott teljesítmény egyenlő, amiből T₁ meghatározható: P = αA(T₁-T_k). Ha például α = 2 Jm^-2 s^-1K^-1, akkor egy 5 méter élű, kocka alakú helyiség 6 kW-os kályhával 0 °C hőmérsékletű környezetben 20 °C-ra fűthető fel. Továbbá fontos kiemelni, hogy a számolás alapját képező reverzibilis fordított Carnot-ciklus jó tájékozódásra szolgál csupán, mivel a valóságos körfolyamat irreverzibilis. Ezért a reverzibilis tárgyalás közelítő eredményt szolgáltat.

Fontos továbbá, hogy a falak α hőátbocsátási tényezője valójában nem állandó, csak kis hőmérsékleti tartományban vehető állandónak. Hő- és áramlási hasonlósági kritériumok segítségével különféle fizikai szituációkban meghatározható α hőmérsékletfüggése. A jelen helyzetben α a hőmérséklet-különbség negyedik gyökével arányos. Ennek meghatározására a Grashoff-, Nusselt- és a Prandtl-féle hasonlósági kritériumokat kell felhasználni. Mivel α értékét számításainkban állandónak vesszük, az eredmények e tekintetben is közelítő érvényűek.

Ezt a modellt tekintve mekkora hűtést lehet elérni? T₂-nek van alsó limitje. Egyik tényező α hőmérsékletfüggése. Ha ugyanis T₁-T₂ nagy, úgy α is egyre nagyobb, tehát romlik a hőszigetelés a környezet (a helyiség) és a hűtött tér között. Egészen más technika, amikor megközelítik az abszolút zérus fokot. E kitérő után határozzuk meg stacionárius állapotban a hűtőgép által befektetendő P mechanikai teljesítményt. Mivel az egy ciklus alatt végzett munka W = PΔt, továbbá felhasználva a jósági tényező formuláját és Q₂ előbbi képletét,

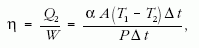
másrészt;

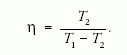
Végül

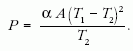
Jól látható, hogy nagyobb hűtés eléréséhez négyzetesen növekvő mechanikai teljesítmény szükséges.

Példaként határozzuk meg a szükséges relatív teljesítménytöbbletet a nyári és téli üzem között, ha a hűtött térben ugyanazt a hőmérsékletet kívánjuk fenntartani. Legyen például T₂ mindig -10 °C, vagyis 263 K, míg a helyiségben télen 18 °C és nyáron 27 °C. Keressük tehát a δ = ΔP/P₁ hányadost. ΔP előbbi képletéből kapjuk, hogy

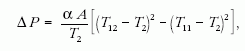
ahol T₁₂ és T₁₁ T₁ értéke nyáron, illetve télen. Végül a relatív teljesítménytöbblet

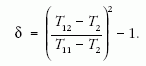
Numerikusan:

A klímaberendezésről

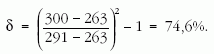
A hűtéshez tartozik egy nálunk is elterjedt eljárás helyiségek hűtésére, illetve klimatizálására. A működés elve itt is a fordított reverzibilis Carnot-ciklus. Most azonban a hőcserélőt - ahol leadódik egy-egy ciklusban az elvont hő - nem a hűtendő helyiségben helyezték el, hanem a lakáson kívül, például a külső falon. Így a gép, rendszerint elektromos energia betáplálásával működő párologtató-áramoltató berendezés a helyiségből elvont hőt a környezetnek adja át, amit állandó hőmérsékletűnek tekintünk. Például a freont helyettesítő gázzal zárt csőrendszerben végeztetjük a fordított Carnot-ciklust. E gépek érdekessége, hogy egy kapcsolóval fűtésre is átállíthatók. A kapcsolóval ugyanis - a zárt csőrendszerben áramoltatott közeg áramlási irányának megváltoztatásával - a párologtató és az úgynevezett kondenzátor szerepe felcserélődik. Ezáltal a gép a környezettől von el hőt és azt a helyiségnek adja le. A csőrendszerben lévő halmazállapot- változások külső munka árán mennek végbe, és ennek révén jut hő az alacsonyabb hőmérsékletű környezetből a melegebb helyiségbe. De "nem magától" megy végbe e folyamat. A jósági tényező viszont más, mint amikor ugyanezt a gépet hűtésre használjuk. Minket ugyanis fűtéskor nem az elvont Q₂ hő, hanem a leadott Q₁ hő érdekel. A befektetett W munkát ehhez kell viszonyítani. Ezért most a jósági tényező (hatásfok):

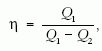
átírva:

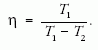
Hűtéskor viszont

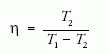
volt a jósági tényező.

Periodikus hőátadás sík falon keresztül

A probléma egyszerűsített modellen igen szemléletesen tárgyalható, a diszkusszió jól rámutat a jelenség lefolyására.

Gondoljunk egy vékony falu házra, annak egyik szobájára. A fal ugyan tégla, de gyengén tartja a meleget. Ilyen lehet például egy nyaraló. Ez esetben a környezeti hőmérséklet ingadozása a különböző napszakokat tekintve, erősen befolyásolja a szoba belterének hőmérsékletét.

Modellszerűen írjuk le a jelenséget. Tudjuk, a modell akkor jó, ha a jelenség lényeges vonásait tükrözi. Emellett még az is szerencsés, hogy egyszerűbb matematikai tárgyalást tesz lehetővé. Ezért az alábbi feltételeket szabjuk: a hőátmenet a falra merőlegesen történik, akár be, akár kiáramlásról van szó. A fal átbocsátását az α hőátbocsátási tényezővel vesszük figyelembe, ami egyszerre írja le a fal két oldalán a hőátadást és a véges vastagságú falban a hővezetést. Így α megadásával sík, vékony falat tekinthetünk. Úgy veszszük továbbá, hogy a helyiségben bárhol a pillanatnyi hőmérséklet ugyanaz. Ezáltal a hővezetés parciális differenciálegyenlete helyett közönséges differenciálegyenletet kell megoldani. Ha pontosabb elemzést követnénk, arra jutnánk, hogy hőmérsékleti hullámok futnának végig a helyiségen lecsengő amplitúdóval. A szemközti falról részben visszaverődve, állóhullámhoz hasonló állapot alakulna ki. Ha elég hosszú rúd hővezetését vizsgálnánk, ahol visszaverődésről nincs szó, ez a számítás alapját képezné a híres &Aumi;ngström-féle mérőeljárásnak. Ezzel lehet ugyanis nagy pontossággal mérni fémek hővezető-képességét. De kövessük most az egyszerűbb modellt.

Fűtsük a helyiséget P teljesítménnyel is, legyen a szobában az összes anyag tömege m, az átlagos fajhő c, a hőcserélő-felület A, a szoba pillanatnyi hőmérséklete T. Legyen továbbá T₀ a környezeti alaphőmérséklet és R a környezeti hőmérséklet-ingadozás maximuma. Végül a környezet hőmérsékletét írja le az alábbi, ω frekvenciájú periodikus időfüggvény:

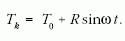
Az előbbiek alapján a szoba hőcseréjére felírhatunk egy energiaegyenletet Newton hőátadási törvényének figyelembe vételével:

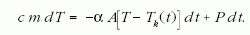
A szögletes zárójeles kifejezés t-től függően lehet pillanatnyilag pozitív vagy negatív. Ezért lehetséges pillanatnyi hőkiáramlás vagy -beáramlás. A megoldandó differenciálegyenlet:

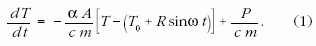
Abban a speciális esetben ha dT/dt = 0 feltételt írjuk elő, (1)-ből adódik, hogy P már nem lehet állandó, mert akkor T időfüggő lenne, ami a tett feltevéssel ellenkezik. Ekkor tehát periodikusan kellene fűteni, hogy T állandó legyen. Ha viszont a külső hőmérséklet nem periodikusan változik, tehát ω = 0 is fennáll, P már lehet állandó és kapjuk a közvetlenül is nyerhető T egyensúlyi hőmérsékletet. Ilyenkor - elemi meggondolással - a leadott teljesítmény egyenlő a kimenővel. Ez adódik a mondott feltevéssel, ami (1)-ből is következik. Tehát

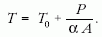
Visszatérve (1) megoldására, átrendezés után a megoldandó differenciálegyenlet:

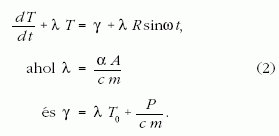
Megoldás: Az inhomogén egyenlet egy partikuláris megoldásához hozzá kell adni a megfelelő homogén egyenlet általános megoldását. Ez utóbbi T_hom = Ke^-λt, ahol K egy állandó. A (2) egyenlet egy partikuláris megoldását próbafüggvény alakjában keressük. Legyen ez

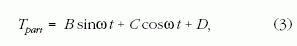
ahol B, C, D meghatározandó állandók. A (3) feltételt a (2) egyenletbe tesszük és együttható összehasonlítással határozzuk meg az előbbi állandókat. Erre nézve egyenletrendszert kapunk:

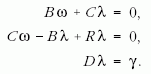
Ezt az egyenletrendszert megoldva, kapjuk az előbbi állandók konkrét értékeit:

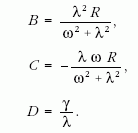
Stacionárius állapotban (jelenleg hosszú időre nézve) a homogén egyenlet megoldása lecseng és ezért (2) stacionárius megoldása:

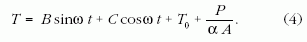
A (4) megoldás diszkussziója tartalmazza a jelenség érdekességét. Ha az első két tagból kiemelünk (B²+C²)^1/2-t, és alkalmazzuk az egyik trigonometrikus addíciós tételt, úgy ismét szinusz-függvénnyel írható le a helyiség periodizáló hőmérséklete. Ez a függvény B, C, D fenti képleteivel ilyen lesz:

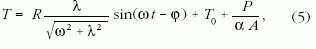
lesz, ahol

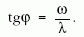
Ezek szerint a helyiségben ugyanazzal a periódussal ingadozik a hőmérséklet, de csökkent amplitúdóval, mivel (5)-ben R szorzója mindig egynél kisebb. Ami külön érdekesség, hogy a fal hatása még abban is jelentkezik, hogy φ fáziskésést hoz létre a hőmérséklet ingadozásában. Minél nagyobb ω, annál nagyobb lesz φ és ugyanakkor annál kisebb a hőmérsékleti amplitúdó. A fal mintegy ellenáll, nem tudja követni az ingadozásokat. Úgy viselkedik, mintha tehetetlensége lenne. Viszont λ által, ha α nagy, érthető módon a belső térben alig csökken a hőmérsékleti amplitúdó és φ is egyre kisebb, vagyis egyre zavartalanabbul engedi át a fal a külső ingadozásokat. Végül ω = 0 esetén visszakapjuk az alapesetet, ha a környezeti hőmérséklet állandó.

Ajánlható mérés itt az lehet, hogy a nap folyamán többször mérjük a külső és belső hőmérsékletet. Ezután felvehetünk egy diagramot ezek időfüggésére, így szemléltetve a kétféle amplitúdót és a két, közelítően szinusz-görbe φ szögű eltolódását.

Megjegyzendő, hogy az amplitúdócsökkenés nem a falban lévő energiadisszipáció következménye, azaz nem a fal nyeli el a beáramlott energia egy részét, hanem stacionárius állapotban úgy hat a fal α révén, hogy kevesebb energiát enged át. Más kérdés, hogy külön meghatározható a fal energiasűrűsége. Ugyanakkor a periodizáló hőmérséklettől függetlenül hőátmenet csak hőmérséklet-különbség esetén lehetséges, amit az (1) egyenlet ír le. Jelenleg időfüggő a hőmérsékleti gradiens.

<>

A demonstrációs kísérletek előnyösen tovább fejleszthetők fizikai mérésekké, ahogy erre történt már utalás. Ezáltal tevőlegesen belenyúlunk egy megismerési folyamatba, bár itt sem valami újnak a felfedezéséről van szó, hanem például a vonatkozó törvényekben szereplő paraméterek konkrét méréséről, mint a hőátbocsátási tényező, vagy rugalmas szál vonalsűrűsége. Ha a jelenség időbeli lefolyását vizsgáljuk, akkor a méréssel a folyamat megragadása jelent mélyebb megértést. Tág tere nyílik a különböző szintű megközelítésnek a tanulók tehetsége szerint.