Fizikai Szemle honlap |
Tartalomjegyzék |
Sükösd Csaba
BME Nukleáris Technika Tanszék
Szilárd Leó születésének centenáriuma alkalmából, Marx György professzor kezdeményezésére 1998-ban került először megrendezésre a Szilárd Leó Országos Középiskolai Tanulmányi Verseny. Azóta a Szilárd Leó Tehetséggondozó Alapítvány és az Eötvös Loránd Fizikai Társulat minden évben megrendezi a versenyt. 2006 óta határon túli magyar anyanyelvű iskolák tanulói részére is megnyitottuk a részvétel lehetőségét. Az idén éltek ezzel először szerbiai vajdasági iskolák: Zentáról a Gimnázium, valamint a Bolyai Tehetséggondozó Gimnázium és Kollégium, továbbá Újvidékről a Gimnazija Svetozar Marković. Örvendetesen folytatódtak az erdélyi iskolákból történő jelentkezések is: Székely Mikó kollégium (Sepsiszentgyörgy), János Zsigmond Unitárius Kollégium (Kolozsvár), valamint a Nagykárolyi Elméleti Líceum (Nagykároly). A határon túli iskolákból összesen húsz első kategóriás (11-12. osztályos) tanulót neveztek be a versenybe. Sajnos, Felvidékről és Kárpátaljáról 2010-ben sem kaptunk nevezéseket. Összesen 251 első kategóriás (a már említett határon túliakon kívül 177 vidéki és 54 budapesti) valamint 140 junior kategóriás (vidékről 118, Budapestről 22) nevezés érkezett.
A 2010. március 1-jén megtartott első forduló (válogató verseny) tíz feladatát az iskolákban három óra alatt lehetett megoldani. Kijavítás után a tanárok azokat a megoldásokat küldték be a BME Nukleáris Technika Tanszékére, ahol a 9-10. osztályos (junior) versenyzők legalább 40%-os, a 11-12. osztályos (I. kategóriás) versenyzők legalább 60%-os eredményt értek el.
Az alábbiakban ismertetjük a válogató verseny - a 2. részben pedig a döntő - feladatait, valamint rövid megoldásukat. Valamennyi feladatra 5 pontot lehetett kapni.
1. feladat
Szilárd Leó életrajzi totó
Megoldás: a helyes tipposzlop: 2, 2, 1, X, 1. Minden helyes válasz 1 pontot ért.
Megjegyzések: az első kérdéssel kapcsolatban: az 1916-os Eötvös Matematikai Versenyt Koródi Albert nyerte, a 18 éves Szilárd Leó akkor a második volt (a fizika versenyt megnyerte). A megadott szakirodalom közül egyesekben azonban csak annyi szerepelt, hogy Szilárd Leó megnyerte mind a matematikai, mind a fizikai Eötvös Versenyt, ezért a Versenybizottság úgy döntött, hogy azokra a megoldásokra is ad egy pontot, akik az első kérdésre 1-gyel válaszoltak.
2. feladat
Miért helyes, illetve miért helytelen úgy elképzelni,
hogy az elektronok az atommag körül ahhoz hasonlóan
keringenek, mint a bolygók a Nap körül? Milyen
jelenségeket lehet jól leírni a modellel, és melyeket
nem?
Megoldás
A modell által jól leírt jelenségek:
A modell hibái:
3. feladat
A gadolínium ezüstös színű, lágy nehézfém. Egyes
izotópjai nagyon jó neutronelnyelők, így ha atomreaktorba
kerül, akkor - a xenonhoz hasonlóan -
reaktorméreg. Mivel a 157Gd atommagok neutronfelvétel
után olyan izotóppá alakulnak, amelyek már nem
nagyon jó neutronelnyelők, ezért egy idő után elfogynak
a neutronelnyelésre alkalmas atommagok. Emiatt
a gadolíniumot kiégő méregnek nevezik. Abban viszont
különbözik a xenontól, hogy a reaktor leállása
után nem szaporodik. Az atomreaktorok teljesítménynövelése
és az üzemanyagciklus meghosszabbítása
érdekében az eddigi 3,82%-os dúsítású kazetták közé
4,2%-os dúsításúakat is helyeznek. Miért célszerű
ilyenkor a reaktorba gadolíniumot is juttatni?
Megoldás
A reaktor teljesítményét - kissé leegyszerűsítve - az aktív zónában lévő hasadóanyag mennyisége és az átlagos neutronfluxus nagysága határozza meg. Az energiatermelési kampány elején még sok a hasadóanyag, ezért kisebb neutronfluxus kell az előírt teljesítmény eléréséhez, mint a kampány végén, amikor az üzemanyag már fogyóban van. A neutronfluxus növekedését a kiégő mérgek - például gadolínium - alkalmazásával is el lehet érni. Ha a gadolínium kezdetben megfelelő arányban van jelen, akkor elérhető, hogy a gadolínium kiégése miatt növekvő neutronfluxus éppen kompenzálja a hasadóanyag fogyásából eredő hatást, és a reaktor teljesítménye akár további szabályozóelemek nélkül is - szinte automatikusan - állandó szinten marad.
Különösen fontos a kiégő mérgek alkalmazása teljesítménynöveléskor, és/vagy kampányidő hosszabbításkor. Ezekben az esetekben több energiát akarunk termelni egy kampány alatt, ezért több hasadóanyagot kell bevinni a reaktorba. Ezt magasabb dúsítású kazettákkal érik el. Nem biztos azonban az, hogy az eredetileg tervezett szabályozóelemek elegendőek arra, hogy a kampány elején az így bevitt többletreaktivitást az előírt biztonsági szinten le tudják kötni. Kiégő mérgek - például gadolínium - alkalmazásával azonban kompenzálni lehet a bevitt többlet hasadóanyag hatását.
4. feladat
Az újságokban a következő hír jelent meg: "Az
ELTE és a KFKI RMKI három kutatóját érte az a megtiszteltetés,
hogy először publikálhattak 2,36 teraelektronvolton
történt ütközéseket. A rekord energiaszintet
a CERN gyorsítójában, az LHC-ben állították
elő, ahol még magasabb energián fogják keresni a
rejtélyes Higgs-bozont. A részecskevadászatban jól
jönnek majd a magyarok mérései." A három magyar
kutató név szerint: Siklér Ferenc, Veres Gábor és Krajczár
Krisztián.
A nyugalmi tömegük hányszorosára nőtt a 2,36 TeV energiát eredményező ütközésben részt vevő, felgyorsított protonok tömege?
Megoldás
Miután a protonok egymással szembe ütköztek, a 2,36 TeV-es ütközési energiát két, egyenként 1,18 TeV = 1,88 · 10-7 J mozgási energiájú proton hozta létre. A protonok nyugalmi tömege 1,672 · 10-27 kg. A mozgási energiát az
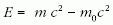
képlettel lehet megadni, ebből
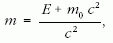
behelyettesítve:
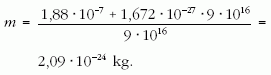
Ez a proton nyugalmi tömegének 1250-szerese.
5. feladat
Becsüljük meg Magyarország összes lakásában lévő
radongáz tömegét! Mekkora lenne e gázmennyiség
térfogata normálállapotban?
Adatok: A 222Rn felezési ideje Tf = 3,8 nap. A lakások légterének átlagos (radonból származó) aktivitása 50 Bq/m3. A lakások számát vegyük 4 milliónak, az átlagos térfogatot pedig V = 60 m2 × 3 m = 180 m3-nek.
Megoldás
Az összes aktivitás:
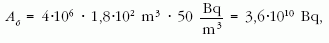
másrészt
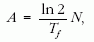
amiből
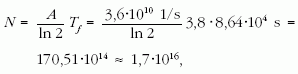
így a radongáz tömege
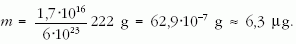
E gázmennyiség térfogata normál állapotban:
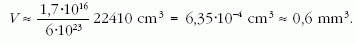
Második (alternatív) megoldás
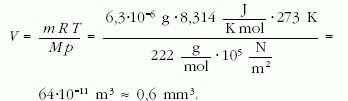
6. feladat
A Nap 3,92 · 1026 W teljesítménnyel sugároz.
Megoldás
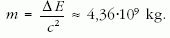
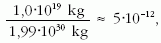
azaz 5 pikonapnyi része.
7. feladat
A Balatonon idén a jég átlagosan 14 cm vastagságúra
"hízott".
Adatok: a Balaton területe 595 km2, a jég hőmérsékletét
vegyük mindenütt 0 °C-nak. A Föld felszínére
érkező napsugár teljesítménye derült időben,
merőleges beesésnél: 600 W/m2. Az energiatermelő
magfúziós folyamat (több közbeeső lépcsőn keresztül):
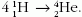 A H és a He atommag tömege rendre:
mH = 1,673 · 10-27 kg,
illetve
mHe = 6,647 · 10-27 kg.
A H és a He atommag tömege rendre:
mH = 1,673 · 10-27 kg,
illetve
mHe = 6,647 · 10-27 kg.
Megoldás
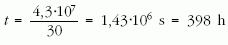
szükséges. A feladat szerint naponta átlagosan csak 6 órát süt a Nap, ezért a 398 órányi napsütéshez 66,4 napra van szükség. Mivel minden egyes négyzetméterre ugyanakkora energia esik, ezért a teljes jégmennyiség felolvasztásához is ugyanennyi időre van szükség.
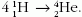 fúzióban
felszabaduló energia a tömeghiányból számolva q =
(4mH-mHe) · c2
= 4,05 · 10-12 J, ennyi energia előállításához
N = Q/q = 0,63 · 1028 magreakció szükséges. Minden
magreakcióban 4 hidrogén vesz részt, így az "elhasznált"
H-atommagok száma: 2,5 · 1028. Egyetlen H-atom tömege
1,673 · 10-27 kg, ezért ennyi energiát -42 kg hidrogén
fúziójával lehet előállítani. (A Napban 66 nap alatt természetesen
ennél sokkal több hidrogén fuzionál, hiszen a
Nap által kibocsátott energiának csak igen kis része fordítódik
a balatoni jég megolvasztására.)
fúzióban
felszabaduló energia a tömeghiányból számolva q =
(4mH-mHe) · c2
= 4,05 · 10-12 J, ennyi energia előállításához
N = Q/q = 0,63 · 1028 magreakció szükséges. Minden
magreakcióban 4 hidrogén vesz részt, így az "elhasznált"
H-atommagok száma: 2,5 · 1028. Egyetlen H-atom tömege
1,673 · 10-27 kg, ezért ennyi energiát -42 kg hidrogén
fúziójával lehet előállítani. (A Napban 66 nap alatt természetesen
ennél sokkal több hidrogén fuzionál, hiszen a
Nap által kibocsátott energiának csak igen kis része fordítódik
a balatoni jég megolvasztására.)
8. feladat
Egy 500 nm hullámhosszúságú monokromatikus fényt
a tér minden irányába egyenletesen kibocsátó, pontszerűnek
tekinthető fényforrás teljesítménye 20 mW.
Megoldás
Az 500 nm hullámhosszúságú foton energiája: E = h · f = h · c/λ = 4 · 10-19 J. A másodpercenként kibocsátott fotonok száma: N = 20 mW/4 · 10-19 J = 5 · 1016 darab.
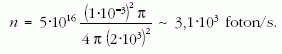
9. feladat
Egy γ-forrás aktivitása 925 kBq. A Geiger-Müller-számlálóval
másodpercenként 160 darab beütést tudunk
regisztrálni, amikor a forrás és a számláló közé
3,2 mm vastag ólomlemezt helyeznek. A lemez eltávolításakor
a beütésszám 280-ra nő másodpercenként.
Megoldás
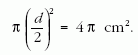
Erre esik 2800 foton másodpercenként, a kibocsátott 925 ezerből. Azaz:
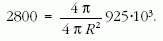
Ebből kapjuk:
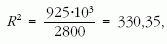
azaz R = 18,18 cm.
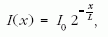
ahol L a felezési rétegvastagság. A feladat éppen erre kérdez rá, hiszen ez az a vastagság, amely az intenzitást a felére csökkenti.
A feladatból tudjuk, hogy
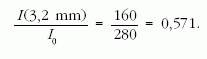
Azaz
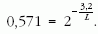
Mindkét oldal logaritmusát véve kapjuk:
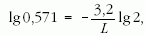
amiből
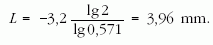
10. feladat
Adatok: 1 kilotonna hagyományos robbanóanyagból 4,184 · 1012 J energia szabadul fel. A bomba robbanását okozó anyag egyetlen atommagjának magreakciójából felszabaduló energia 32 pJ.
Megoldás
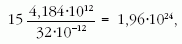
azaz 3,27 mol. A bomba hasadóanyaga zömében 235- ös tömegszámú urán. A láncreakcióban résztvevő urán tömege tehát 3,27 · 235 = 768 g, ami a bombában lévő hasadóanyag tömegének körülbelül 1,2%-a.
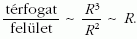
Innen látható, hogy a bomba sugarának növelésével ez az arány javítható, és megfelelő hasadóanyag esetén van olyan méret, amikor ez az arány eléri az önfenntartó láncreakcióhoz szükséges értéket.
Az elődöntő feladatait 72 fő I. kategóriás - Budapestről 20-an, vidékről 51-en, valamint 1 határon túli - és 18 fő junior - 3 budapesti és 15 vidéki - versenyző teljesítette olyan szinten, hogy dolgozataikat a javító tanárok tovább tudták küldeni a BME Nukleáris Technika Tanszékére további rangsorolás végett.
A verseny krónikájához hozzátartozik, hogy az egyik iskolából három diák dolgozatát hibás kategóriajelzéssel küldték tovább: érettségi előtt álló diákokat junior kategóriájúaknak tüntettek fel. A verseny meghirdetésében szerepelt, ha valaki nem a megfelelő kategóriában versenyez, akkor a Versenybizottság kizárhatja. Az esetet kivizsgálva a Versenybizottság megállapította, hogy a kategória téves megadása a javító/felkészítő tanár hibája. Ezért olyan döntés született, hogy a vétlen diákokat nem büntetjük, nem zárjuk ki a versenyből (azaz I. kategóriás diákként versenyezhetnek tovább), de eredményüket nem számítjuk be a tanári Delfin-díj pontversenyébe, s nem vesszük figyelembe a Marx György vándordíjért való versenyben sem. A három diák közül kettő eredménye elegendő volt az I. kategória döntőjébe jutásához, így ők továbbjutottak.
A beküldött dolgozatokat ellenőrizve egy egyetemi oktatókból álló bírálóbizottság a legjobb 10 junior versenyzőt és a legjobb 20 első kategóriás versenyzőt hívta be a paksi Energetikai Szakközépiskolában 2010. április 24-én megrendezett döntőre. Külön örömet jelentett, hogy az idén először egy határon túli tanuló - Sipos E. Lehel Sepsiszentgyörgyről - is olyan szép eredményt ért el, amivel bekerült a meghívottak közé. Sajnos a döntő előtt értesítést kaptunk: mégsem tud részt venni a döntőn. Néhány további diák is lemondta a versenyt a Kémia OKTV-vel való ütközés miatt, így végül 18 fő I. kategóriás, és 9 fő junior kategóriás diák versenyzett.
Az idén csak három lány jutott be a verseny döntőjébe, ketten az I. kategóriában, egy pedig a juniorok között. A verseny fordulóin (mobiltelefon és Internet kivételével) bármilyen segédeszközt használhattak a diákok.
A Fizikai Szemle következő számában a döntő feladatairól és értékeléséről, a helyezésekről, valamint a tanári Delfin-díj és a Marx György vándordíj nyerteseiről számolunk be.