ÜTKÖZÉSEK ELEMZÉSE ENERGIA-IMPULZUS DIAGRAMOKKAL

Bokor Nándor
BME, Fizika Tanszék

Hasznosak lehetnek a relativisztikus ütközések tanításánál az energia-impulzus diagramok [1], amelyekben a szokásos Minkowski-diagramokon szereplő idő- és a helykoordináták szerepét az energia és az impulzus veszi át. Mint az alábbiakban látható lesz, az ilyen diagramok fő vonzereje abban rejlik, hogy az ütközés előtti és utáni állapotokat egyszerre jeleníti meg, és hogy az összes lényeges fizikai paraméter (a tömegpontok tömege, sebessége, impulzusa, energiája) azonnal leolvasható az ábráról.

Az egyszerűség kedvéért a képleteket végig c = 1 egységekben fogom felírni [2]. Ez azt jelenti, hogy a t időt hosszúságegységben mérjük (például méterben), a v sebesség nagysága pedig 0 és 1 közé eső dimenzió nélküli szám. Ugyanebből a konvencióból az is következik, hogy az m tömeg, az E energia és a p impulzus mind ugyanabban az egységben mérendők. Ez az egység lehet például kilogramm, joule, erg, elektrontömeg stb. Hogy konkrétan melyiket választjuk, annak a jelen cikkben nincs jelentősége, ezért hacsak külön nem jelölöm, mindenütt az a.u. ("arbitrary unit", azaz "tetszőleges egység") megjelölés értendő a számérték után.

A téridő-beli Minkowski-diagramokat széles körben alkalmazzák a relativitáselmélet tanításában. Ezeken egy-egy pont egy-egy eseményt jelöl, amelynek koordinátáit (t, x) alakban, vagy (t, x, y) alakban szokás megadni, attól függően hogy két- vagy háromdimenziós diagramról, azaz egy vagy kettő térbeli dimenziójú tárgyalásmódról van szó. Megállapodás szerint a függőleges tengelyen szokás a t időkoordinátát, a vízszintes tengely(ek)en pedig a térbeli koordinátá(ka)t ábrázolni. Három térbeli dimenziójú Minkowski-diagramot nem tudunk készíteni, hiszen négydimenziós ábrázolásra lenne hozzá szükség. Szerencsére a relativisztikus jelenségek nagy részének tárgyalásához nyugodtan elhagyható a harmadik térbeli dimenzió.

Minkowski-diagramokat az energia-impulzus térben is konstruálhatunk [1]; ekkor a függőleges tengelyen az E energia, a vízszintes tengely(ek)en pedig a p impulzus szerepel. Az ilyen diagramokon egy-egy (E, p) - vagy (E, p_x, p_y) - pont valamilyen tömegpont adott állapotát jelöli: megadja energiáját és azt az impulzust, amellyel a tömegpont éppen mozog. Az energia és az impulzus alább felírt relativisztikus képleteiből megérthetjük a diagramok néhány általános jellemzőjét:

és 1 dimenzióban

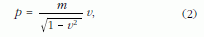
illetve 2 dimenzióban

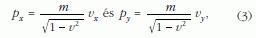
amelyek a tömeg, energia és impulzus közötti jól is- mert összefüggéshez vezetnek:

A (4) egyenlet a tömeg invarianciáját fejezi ki. Egy adott tömegpont energiájára különböző inerciarendszerbeli megfigyelők különböző számértékeket fognak kapni, mint ahogyan az impulzusára is; az eltérő számoknak az a különleges algebrai kombinációja azonban, amely a (4) egyenlet bal oldalán szerepel, minden megfigyelő számára ugyanazt a számértéket szolgáltatja: a tömeg invariáns.

A (4) egyenletből leolvasható, hogy az energia-impulzus diagramokon egy adott m tömegű tömegpont összes lehetséges állapota ugyanazon a hiperbolán - illetve 2D mozgásnál ugyanazon a forgási hiperboloidon - fekszik. (Ez a tény természetesen szoros kapcsolatban van a téridő-intervallum invarianciájával; a téridőbeli Minkowski-diagramokon analóg módon hiperbolákat használunk például arra, hogy a különböző vonatkoztatási rendszerekhez tartozó koordinátatengelyeket egymáshoz kalibráljuk.) Az a vektor, amelyet az origóból e hiperbola - vagy hiperboloid - megfelelő pontjához húzunk, az adott tömegpont energia-impulzus vektora.

Az energia-impulzus vektor közvetlen vizuális információt ad a tömegpontnak az ütközés szempontjából lényeges összes tulajdonságáról: a vektor által meghatározott hiperbola - vagy hiperboloid - és az E-tengely metszéspontja megadja a részecske tömegét; a vektor E-tengelyhez képesti meredeksége pedig a részecske sebességét. Különösen vonzó tulajdonsága az ilyen diagramoknak az, hogy például egy tömegpontrendszer teljes energiáját és teljes impulzusát egyetlen lépésben láthatóvá lehet tenni: csupán meg kell szerkeszteni az egyes energia-impulzus vektorok vektori összegét, és leolvasni az összegvektor függőleges, illetve vízszintes komponenseit.

Az alábbiakban azt tekintem át, hogyan olvasható le egyetlen pillantással mind a rugalmatlan, mind a rugalmas ütközések szinte valamennyi fontos adata az energia-impulzus diagramokról.

Ütközések

Az ütközésekkel kapcsolatos számpéldákban általában adottak az ütközésben résztvevő tömegek és kezdeti sebességeik; a diákoknak ezután az a feladatuk, hogy kiszámítsák

1. ) az ütközéskor keletkezett egyetlen test tömegét és sebességét (tökéletesen rugalmatlan ütközés esetén, amit az egyszerűség kedvéért röviden rugalmatlan ütközésnek fogok nevezni)
2. ) az ütköző tömegpontok végsebességét (rugalmas ütközés esetén)

Rugalmatlan ütközés két tömegpont között

Az 1. ábra egy olyan rugalmatlan ütközés energiaimpulzus diagramját mutatja, amelyben egy mA és egy m_B tömegű részecske vesz részt. A tömegek és a sebességek a következők: m_A = 1 [a.u.], m_B = 2 [a.u.], v_A =-0,5, v_B =-0,6.

Az ütközés során a két tömegpont "összetapad" egyetlen, m_C tömegű (továbbra is pontszerűnek tekintett) testté, amely v_C sebességgel indul tovább. Az összetapadt test energia-impulzus vektora a két ütköző tömegpont energia-impulzus vektorának összege.

Ha felírjuk és megoldjuk az energiamegmaradás és az impulzusmegmaradás egyenletét, az m_C = 3,536 [a.u.] és v_C = 0,252 számértékeket kapjuk.

Bár az 1. ábráról nem látszanak ilyen sok tizedesjegyre a fenti számértékek, de azért az ütközés "teljes sztorija" leolvasható belőle, ráadásul kvantitatív válaszokat kapunk minden lényeges kérdésre: mindhárom test tömegét látjuk, ha leolvassuk, hol metszi az E-tengely a megfelelő hiperbolákat; a három tömegpont sebességét a megfelelő energia-impulzus vektor (E-tengelyhez képesti) meredeksége mutatja; energiájukat és impulzusukat pedig ugyanezen a vektorok függőleges, illetve vízszintes komponense.

Az ütközés kimenetele, így m_C és v_C értéke is egyértelműen meghatározott. A rugalmatlan ütközések szokásos, algebrai tárgyalásakor ezt a tényt általában úgy magyarázzuk, hogy két ismeretlen meghatározásához éppen két független egyenlet (az energiamegmaradás és az impulzusmegmaradás) áll rendelkezésünkre. Ha azonban az 1. ábrához hasonló energiaimpulzus diagramot használunk, a megoldás egyértelműségének oka triviálisan látszik: az összetapadt testet az ábrán egy olyan vektor képviseli, amelyet két vektor összegeként kaptunk, és természetesen ennek az összegvektornak mind "hossza" (azaz m_C ), mind iránya (azaz v_C ) egyértelműen meghatározott.

A rugalmatlan ütközések során a végállapot, azaz a keletkezett test m_C tömege és v_C sebességvektora a térbeli dimenziók számától függetlenül mindig egyértelmű. Algebrai tárgyalásmód esetén ezt úgy magyarázzuk, hogy a dimenziószám növelésekor amilyen mértékben növekszik az ismeretlenek száma (azaz v_C komponenseinek száma), ugyanolyan mértékben növekszik a független egyenletek száma is (mindig egy-egy újabb komponensegyenlethez jutunk az impulzusvektor megmaradásából). Így az ismeretlenek száma mindig megegyezik a független egyenletek számával. Az energia-impulzus diagramos tárgyalásmódban ismét egyszerűbb az érvelés: a keletkezett test energia-impulzus vektorát két energia-impulzus vektor összegeként kapjuk, tehát "hossza" (azaz m_C) és iránya (ami v_C komponenseit adja) egyértelműen meghatározott.

Az 1. ábra tömegpontok összetapadására, fúziójára nyújt példát. Az ilyen kölcsönhatások egyik legfontosabb jellemzője a tömegnövekedés: m_C > m_A+ m_B, hiszen a kezdeti mozgási energia egy része az új test nyugalmi energiájának - tömegének - növelésére fordítódott. Az ábra ezt a jelenséget is közvetlenül mutatja, sőt az m_C - (m_A + m_B) tömegnövekedés mértéke is számszerűen leolvasható.

A tömegnövekedés mértéke annál kisebb, minél inkább közelítenek a függőlegeshez az 1. ábra energia- impulzus vektorai, azaz minél kisebbek az ütközésben előforduló sebességek. (Teljesen függőleges vektorok - álló tömegpontok - összekombinálása az E-tengely mentén zajlik, ilyenkor - a tengely lineáris kalibrálása miatt - triviálisan teljesül a tömegmegmaradás: az összetapadt test tömege egyenlő a két kiindulási tömeg összegével.) Az 1. ábra alapján így érthető például az is, hogy bár a középiskolában rugalmatlan ütközési típuspéldaként tárgyalt ballisztikus inga esetében is van tömegnövekedés - a lövedék kezdeti mozgási energiájának hővé (a zsák-lövedék rendszer belső energiájává) alakuló része valóban megnöveli a rendszer tömegét -, azt a tömegnövekedést teljes joggal hanyagoltuk el.

Az 1. ábrán bemutatott rugalmatlan ütközést "időben visszafelé is lejátszhatjuk", ez olyan jelenségek tárgyalásához vezet minket, mint a maghasadás, vagy egy bomba felrobbanása darabokra stb. Természetesen ilyen esetekben is az 1. ábrához hasonló diagramot kapunk; ekkor azonban a tömegdefektus lesz leolvasható az ábráról.

Egy dimenziós rugalmas ütközés két tömegpont között

Tekintsünk most egy rugalmas ütközést ugyanolyan kezdőfeltételekkel, mint az 1. ábrán. Feladat: meghatározni a két tömegpont v_A' és v'_B végsebességét, miután visszapattantak egymásról. Az energia-impulzus diagram "nyelvére fordítva" ez azt jelenti, hogy két olyan energia-impulzus vektort keresünk, amelyek kielégítik az alábbi feltételeket:

1. összegük ugyanazt az energia-impulzus vektort kell adja, mint az kiindulási két energia-impulzus vektor összege (azaz összegük a C pontba kell hogy mutasson);
2. a két keresett vektor végpontja az m_A, illetve m_B jelzésű hiperbolára kell mutasson, hiszen az ütközés után az eredeti két tömegpont halad tovább.

A probléma egyszerűen megoldható a következő geometriai módszerrel (2. ábra): a C pontból, mint origóból, rajzoljuk fel az m_A hiperbolát fejtetőn. Ez az invertált hiperbola (amelyet a 2. ábrán "m_A" felirattal jelöltem) az m_B hiperbolát két pontban metszi. Mindkét metszéspont teljesíti a fenti feltételeket; ráadásul csak ez a két metszéspont ilyen. A két metszéspont fizikai jelentése: ezek képviselik azokat az állapotokat, amelyeket ebben a kölcsönhatásban az m_B tömegű tömegpont felvehet. Egyikük (a 2. ábrán B-vel jelölt pont) az m_B ütközés előtti állapotát jelzi; a másikuk (az ábrán B'-vel jelölt pont) ugyanezen tömegpont ütközés utáni energia-impulzus vektorát adja. Mint az ábrán látszik, a vektorösszeadás paralelogramma- szabályát alkalmazva egyszerűen megrajzolható ezek után az m_A tömegű tömegpont ütközés utáni energia-impulzus vektora is (ezt A' jelzi az ábrán). Ismét az ütközés teljes történetét megtudjuk egyetlen ábrából: az összes sebesség-, energia- és impulzusadat, mind ütközés előtt, mind ütközés után, kvantitatíven látszik az ábrán. (A keresett két végsebesség, v'_A és v'_B például a végső energia-impulzus vektorok meredeksége.)

Egy dimenziós rugalmas ütközés esetén v'_A-ra és v'_B-re egyértelmű megoldást kapunk. Csakúgy, mint a rugalmatlan ütközéseknél, algebrai okoskodással ezt úgy magyarázzuk, hogy az ismeretlenek és a független egyenletek száma megegyezik: két egyenlet (energiamegmaradás és impulzusmegmaradás) két ismeretlenre. A 2. ábra energia-impulzus diagramja azonban "a sztorinak" ezt a részét is első pillantásra "elmeséli": ha két hiperbola metszi egymást, pontosan két metszéspontjuk van. Az egyik metszéspont a tömegpontok kiindulási állapotának felel meg. A másik egyértelműen meghatározza a tömegpontok ütközés utáni állapotát.

Két dimenziós rugalmas ütközés két tömegpont között

Az előző gondolatmenet egyszerűen általánosítható olyan ütközésekre, amelyek két térbeli dimenzióban zajlanak. Az energia-impulzus diagram három dimenziós ábrává alakul, amelyben az ütköző tömegpontokat nem egy-egy hiperbola, hanem egy-egy forgási hiperboloid jelképez, mint az a (3) és (4) egyenletekből leolvasható. A 3.a ábrán egy ilyen diagram látható, ugyanazokra a kezdőfeltételekre, mint az 1. és 2. ábrák. (A tömegpontok ütközés előtt az x-tengely mentén mozogtak.) A 2. ábra magától értetődő általánosításaként most az m_A hiperboloidot rajzoljuk fel fejtetőn (ismét a C pontot origónak tekintve). Ennek az invertált hiperboloidnak (amelyet az ábrán "m_A" felirat jelöl) és az m_B hiperboloidnak metszésgörbéje adja azon energia-impulzus vektorok végpontjait, amelyekkel az m_B tömegpont ebben a kölcsönhatásban rendelkezhet.

Két dimenziós rugalmas ütközéseknél végtelen sok végállapot lehetséges. Ezt algebrai úton úgy szoktuk magyarázni, hogy négy ismeretlenünk van (a v_A' és v'_B végsebességek x- és y-komponensei), viszont meghatározásukhoz csak három független egyenlet áll rendelkezésünkre (az energiamegmaradás, illetve az impulzusmegmaradás mindkét komponensre). Az energia-impulzus diagramra azonban ismét elég egyetlen pillantást vetnünk, hogy szemléletes magyarázatot kapjunk a lehetséges végállapotok végtelen számára: a két hiperboloid folytonos görbe mentén metszi egymást (nem csupán két pontban, mint az egy dimenziós esetben, lásd 2. ábra), és a metszetgörbe minden pontja egy-egy lehetséges megoldást ad.

A 3.b ábrán a két hiperboloid metszetgörbéje, egy megdöntött ellipszis látható. Az ábrán szereplő A' és B' energia-impulzus vektorok a két tömegpontnak csupán egy ütközés utáni konfigurációját jelenítik meg a végtelen sok lehetséges esetből. (Éppen azt az esetet, amikor az m_B tömegpont a negatív y irányban mozog az ütközés után.) Az ábrán láthatók az A-val és B-vel jelölt, ütközés előtti energia-impulzus vektorok is.

A metszetgörbét levetítve a (p_x, p_y síkba egy újabb ellipszist kapunk, ez a 3.b ábra szaggatott görbéje. A 3.c ábra részletesebben mutatja ezt a (p_x, p_y) síkba levetített ellipszist. A "_p" alsó indexszel jelölt pontok mind a 3.b ábra megfelelő pontjainak levetítései a (p_x, p_y) síkba. (A B_p pont egy újabb lehetséges végállapotot mutat, amely nem szerepelt a 3.b ábrán.) Ez a fajta részleges "impulzus-diagram" is hasznos lehet pedagógiai szempontból. Ha az O origót összekötjük az ellipszis bármely pontjával, az m_B tömegpont egy lehetséges impulzusvektorát kapjuk, az abból az ellipszispontból C_p -be húzott vektor pedig az az impulzusvektor, amellyel ugyanekkor az m_A tömegpont rendelkezik. A rendszer teljes impulzusvektora mindem kombinációra az OC_p vektor. (Az illusztráció kedvéért az ábrán - kis körökkel - feltüntettem az ellipszis két fókuszpontját is.)

Speciális esetek

Kétdimenziós ütközés két azonos tömegpont között, amelyek közül az egyik nyugalomban van.

A kétdimenziós ütközések gyakran tárgyalt speciális esete, amikor két azonos tömegű részecske ütközik össze (azaz m_A = m_B), és egyikük az ütközés előtt nyugalomban van. A newtoni mechanikából könnyen levezethető ezen ütközéstípusnak az az érdekes tulajdonsága, hogy ütközés után a két tömegpont mozgása egymásra merőleges. Impulzus-diagramok segítségével szépen illusztrálható, hogy ez az eredmény csak kis kezdősebességeknél érvényes.

A 4. ábra ilyen ütközésekre mutatja az impulzusdiagramokat, a következő paraméterek mellett: m_A = m_B = 1 [a.u.], és v_A = 0,9, 0,5 és 0,1 (ilyen sorrendben az a), b) és c) ábrákon). A 3.c ábrához hasonlóan - és a relativisztikus tárgyalásnál mindig - itt is mindenütt egy-egy ellipszis írja le az ütközés utáni lehetséges állapotokat. (Az ellipszisek fókuszpontjait ismét kis körök jelzik az ábrán.) Ebben a speciális esetben azonban O és C_p (a teljes impulzusvektor kezdőpontja és végpontja) nem más, mint az adott ellipszis nagytengelyének két végpontja. A 4. ábrán a teljes impulzust vastag vonallal húzott vízszintes vektor ábrázolja; a két tömegpont ütközés utáni impulzusainak néhány lehetséges konfigurációját pedig pontozott vonalú vektorok jelzik. A 4.a ábrából látható, hogy nagy kezdősebességnél az ütközés utáni impulzusvektorok egymással bezárt szöge jelentősen eltérhet a 90°-tól.

Ahogy közelítünk a klasszikus esethez (azaz ahogy v_A csökken), az ütközés utáni impulzusok relatív helyzete egyre inkább közelít a merőlegeshez: csökkenő v_A mellett ugyanis az ellipszis excentricitása csökken, a diagram pedig egyre inkább körhöz kezd hasonlítani. Newtoni közelítésben a diagram pontosan kör, amelynek OC_p az átmérője; így bármely lehetséges impulzus-konfiguráció egy kör átmérője fölé húzott két szomszédos húrnak felel meg, amelyekről Thalész tételéből tudjuk, hogy merőlegesek.

A 4. ábráról az is leolvasható, hogy a teljes impulzus mA vA newtoni képlete mennyiben tér el a helyes relativisztikus eredménytől, és hogyan közelíti meg azt kis sebességeknél. A teljes impulzus, azaz az O és C_p pontok közötti távolság, a 4.a, 4.b és 4.c ábrán 2,06, 0,58 és 0,10 értékűnek adódik. A megfelelő newtoni számértékek: 0,90, 0,50 és 0,10.

Compton-szórás

A két dimenziósként tárgyalható ütközések egy másik speciális esete a Compton-szórás: itt egy foton ütközik egy nyugalomban levő elektronnal. A foton energiájának egy része átadódik az elektronnak, így az mozgásba lendül valamilyen irányban, míg maga a foton egy másik irányba szóródik. Energiavesztesége abban nyilvánul meg, hogy hullámhossza eltolódik (nagyobb hullámhosszak felé).

Fotonra E²-p² = 0, tehát a fotonokat az energiaimpulzus diagramon egy kúpfelület reprezentálja (lásd a ph_A -val jelölt kúpot az 5.a ábrán). Fontos megjegyezni, hogy a téridőbeli Minkowski-diagramok jól ismert "fénykúpjaival" ellentétben az 5.a ábrán szereplő kúp az összes fotont jelképezi, amelyek az (x, y) síkban bármikor, bárhol mozognak. A fotonok nulla tömegű részecskék, ez a tulajdonságuk azonnal látszik az 5.a ábrán, hiszen a kúp olyan elfajult hiperboloidnak tekinthető, amely az E-tengelyt E = 0-ban metszi.

Az elektront az m_B jelű hiperboloid jelképezi. Az egyszerűség kedvéért az ebben a példában előforduló összes tömeg-, energia- és impulzusértéket az elektrontömeg egységeiben (u.e.m., "units of electron mass") fejezem ki, azaz például m_B = 1[u.e.m.]. A bejövő fotonról feltesszük, hogy a pozitív x-tengely mentén mozog, E_A = p_A = 0,5 [u.e.m.] energiával.

A lehetséges végállapotok megtalálásának geometriai módszere hasonló a 3.a ábrán szereplő eljáráshoz. Először meghatározzuk a rendszer teljes energiaimpulzus vektorát (jelen paramétereinkkel ennek E-komponensére 1,5, p_x-komponensére pedig 0,5 adódik). A vektor csúcsát a C pont jelzi az 5.a ábrán. C-ből ezután megrajzoljuk a foton-kúpot fejjel lefelé (ezt "ph_A" jelöli az ábrán). Az m_B hiperboloid és a "ph_A" invertált kúp metszetgörbéje mutatja az elektron lehetséges végállapotait a kölcsönhatás után.

Az 5.b ábrán a metszetgörbe látható (amely ismét egy megdőlt ellipszis). Ugyanezen az ábrán az A és B pontok a foton és az elektron kezdeti energia-impulzus vektorát jelölik, az A' és B' pontok pedig a foton és az elektron egy lehetséges végállapot-konfigurációját.

A 3.b ábrához hasonlóan a metszet-ellipszist ezután levetíthetjük a (p_x, p_y) síkra. A levetített ellipszist az 5.c ábra mutatja. Ezen az ellipszisen két feltűnő sajátosság figyelhető meg a 3.c ábrához képest (amely egy általánosabb ütközést írt le két tömegpont között):

1. a nagytengely bal oldali végpontja az origóban van;
2. a Cp pont, vagyis a C pont levetítése az ellipszis jobb oldali fókuszpontjába esik.

Az 5.c ábrán a B_p' és a B_p" pontok két lehetséges végállapotot jelölnek. Ha az origót összekötjük az ellipszis bármely pontjával, az elektron egy lehetséges impulzusvektorát kapjuk, az abból az ellipszispontból C_p-be húzott vektor pedig a szóródott foton megfelelő impulzusvektorát. Az elektron és foton egymáshoz viszonyított lehetséges mozgásirányai tehát azonnal látszanak az ábrából. A foton különleges részecske: impulzusvektorának hossza egyben megadja energiájának számértékét is. (Mint arról az alábbiakban még szó lesz, az ellipszis pontos alakja függ a bejövő foton energiájától. Ugyanakkor a fotonenergiától függetlenül minden "Compton-ellipszis" rendelkezik a fent felsorolt két geometriai sajátossággal.)

A Compton-szórás néhány kvalitatív jellemzője közvetlenül leolvasható az 5.c ábráról:

1. a szóródott fotonoknak feltétlenül kisebb az energiája (azaz nagyobb a hullámhossza), mint a bejövő fotonnak;
2. a szórási szög növekedésével csökken a szóródott foton energiája, minimális energiája (azaz maximális hullámhossza) a hátrafelé szóródott fotonnak van.

Folytassuk az 5.c ábrán szereplő Compton-ellipszis elemzését. Ehhez egy kis számolásra is szükségünk van. Először határozzuk meg az ellipszis egyenletét. Az m_B hiperboloid egyenlete

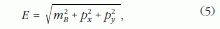
a "ph_A" invertált kúpé pedig

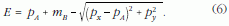
Az (5) és (6) egyenletek jobb oldalát egyenlővé téve, és a kapott összefüggést átrendezve megkapjuk a metszetellipszis (p_x, p_y) síkba levetített képe, azaz a "Compton-ellipszis" egyenletét:ű

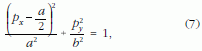
ahol a fél nagytengelyre

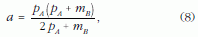
a fél kistengelyre pedig

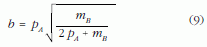
adódik. A fókusztávolság:

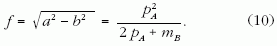
A (8)-(10) összefüggéseket felhasználva az ellipszis e excentricitására és Π paraméterére a következő egyszerű képleteket kapjuk:

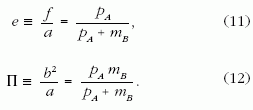
Az e excentricitás azt fejezi ki, hogy ellipszis alakja "mennyire tér el" a körtől (ha e→0, az ellipszisből kör lesz, a két fókuszpont pedig egybeesik a kör középpontjával). A (11) egyenletből ezek után látható, hogy a Compton-ellipszis excentricitásának fizikai tartalma is van: ha a bejövő foton energiája sokkal kisebb, mint az elektron tömege (azaz ), az ellipszisből kör lesz, a szóródó foton lehetséges impulzusvektorai pedig ezen kör rádiuszai mentén helyezkednek el (lásd 5.c ábra). Ilyen esetekben tehát a foton csak mozgási irányát változtatja meg, miközben energiája gyakorlatilag változatlan marad.

Az ellipszis egyenlete egy olyan polár-koordinátarendszerben veszi fel legegyszerűbb és legelegánsabb algebrai alakját, amelynek origója az egyik fókuszpontban van. Az egyenlet ekkor az origóból húzott rádiuszvektor r hosszát adja meg a θ polárszög függvényében:

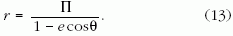
Amint az 5.c ábrából látszik, a Compton-ellipszis esetében a Θ fotonszórási szöghöz tartozó "rádiuszvektor" hossza éppen az ehhez a szórási szöghöz tartozó p_A? fotonimpulzus. Így a (13) egyenletet a Compton-ellipszisre felírva, és e és Π értékét a (11) és (12) kifejezésekből behelyettesítve a

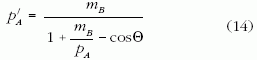
összefüggés adódik. Helyettesítsük be a kölcsönhatás előtti és utáni fotonimpulzusra a

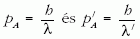
de Broglie-összefüggéseket (ahol h a Planck-állandó), és szorozzuk be (14) mindkét oldalát a jobb oldal nevezőjével. Ezzel

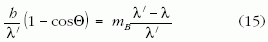
adódik, azaz

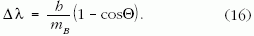
A Compton-szórás jól ismert hullámhossz-eltolódási képletét tehát mintegy a Compton-ellipszis geometriai tulajdonságaiból kaptuk meg, nem pedig a szokásos tisztán algebrai módszerrel (amelyben felírjuk az energiamegmaradás és az impulzusmegmaradás egyenletrendszerét, majd kiküszöböljük belőlük az elektron végsebességét és haladási irányszögét). Az itt felvázolt levezetés ugyan nem feltétlenül egyszerűbb, mint a tisztán algebrai módszer, de valószínű, hogy sok diák számára vonzóbb és elegánsabb ez a fajta geometriai okoskodás, annál is inkább, mert az elektron végsebessége és szóródási szöge fel sem bukkan benne.

Összefoglalva: az energia-impulzus diagramok - az algebrai tárgyalás kiegészítőjeként - hasznos pedagógiai segédeszközt nyújthatnak különféle kölcsönhatások elemzéséhez. A diákok egyetlen ábrára rápillantva ellenőrizhetik a kölcsönhatás minden fontos fizikai sajátosságát, sőt a lényeges fizikai mennyiségek közelítő számértékét is leolvashatják róla.

Irodalom

1. E. J. Saletan: Minkowski diagrams in momentum space. Am. J. Phys. 65/8 (1997) 799-800.
2. lásd például: E. F. Taylor, J. A. Wheeler: Téridőfizika. Typotex, Budapest, 2006.

_______________________

Köszönetemet fejezem ki Hraskó Péternek támogató bírálatáért és hasznos javaslataiért.