XIII. SZILÁRD LEÓ NUKLEÁRIS TANULMÁNYI VERSENY II. rész: a döntő feladatai, a verseny értékelése

Sükösd Csaba
BME Nukleáris Technika Tanszék

I. Kategóriájú feladatok¹

1. feladat (kitűzte: Sükösd Csaba)
Egy speciális füstérzékelő berendezés a mellékelt ábrán látható felépítésű. Az egymástól d távolságra helyezett radioaktív forrás és az alfa-detektor közé áramlik be a külső levegő.

1. ) Vajon ez a berendezés alfa-detektor alfa-forrás ugyanúgy viselkedik Nápolyban (Olaszország, tengerszint) és La Pazban (Bolívia, 3631 m tengerszint felett)?
2. ) Ha igen, miért? Ha nem, akkor hogyan korrigálhatjuk a berendezés eltérő viselkedését?

Megoldás: Az ábrán látható füstérzékelő berendezés működése az alfa-részecskék levegőben mért hatótávolságának mérésén alapul. A levegőréteg d vastagságát úgy kell megválasztani, hogy az alfa-részecskék még éppen elérjék a detektort. Ha füst is keveredik a levegőbe, akkor a füstrészecskék miatt a levegőfüst keverékben lecsökken az alfa-részecskék átlagos hatótávolsága, kevesebb alfa-részecske éri el a detektort, lecsökken a beütésszám, és a készülék riaszt.

1. ) La Pazban a nagy tengerszint feletti magasság miatt a levegő sokkal ritkább, mint Nápolyban, ezért az alfa-részecskék hatótávolsága is nagyobb. Emiatt nagyobb füstkoncentráció kell La Pazban ahhoz, hogy a készülék riasszon, mint Nápolyban.
2. ) Ezt természetesen ki lehet küszöbölni azzal, hogy a berendezést a helyi viszonyokhoz kalibrálják, azaz megváltoztatják a detektor-forrás távolságot.

2. feladat (kitűzte: Papp Gergely)
A paksi reaktorok primerköri vízében oldott bórsav található.

1. ) Mi ennek az oka?
2. ) Miért tilos a reaktort egy adott értéknél nagyobb bórsav-koncentráció mellett üzemeltetni?

Megoldás: A bórsavat a reaktivitás szabályozására használják, mivel a bór igen jó neutronelnyelő. A paksi reaktorok nyomottvizesek, itt a moderálást a hűtővíz végzi. Normális esetben, ha a reaktor teljesítménye nő, a víz hőmérséklete is nő, a víz kitágul. Ezáltal csökken az egységnyi térfogatban lévő hidrogénmagok száma, ami miatt a moderálás csökken. Így a reaktivitás - s ezzel a teljesítmény - csökken, a víz hőmérséklete csökken, újra besűrűsödik stb. Ezt negatív visszacsatolásnak hívják, és biztonsági-szabályozási szempontból nagy jelentősége van. A víz tágulásával azonban a bór mennyisége is csökken térfogategységenként, ezáltal az egységnyi térfogat neutronelnyelő- képessége is. Ez viszont a reaktivitást növeli, és így pozitív visszacsatolást okoz. Ha a bórsav koncentrációja túl magas, akkor ez ellensúlyozhatja, vagy át is lépheti a moderátor tágulása által okozott szabályozó hatást, és a reaktorban pozitív visszacsatolás jelentkezik. Ez önmagában még nem végzetes, mert sok, független visszacsatolás létezik még ezen kívül is. A reaktorokat viszont csak úgy szabad üzemeltetni, ha minden visszacsatolás negatív.

3. feladat (kitűzte: Czifrus Szabolcs)
Egy átlagos ház tömege 100 tonna körül van, az építőanyagokban 10^–4 tömegszázalék urán található.

1. ) Becsüljük meg, hogy egy átlagos családi ház falaiban, alapjában, szerkezeteiben összesen mekkora tömegű urán található és ennek mekkora az aktivitása!
2. ) Van-e ennek valamilyen hatása a bent élő emberekre?

Útmutatás: Elegendő a ²³⁸U izotóp aktivitásával számolni, amelynek felezési ideje 4,5 milliárd év.

Megoldás: 100 tonna = 10⁵ kg, ebben átlagosan 10⁵ · 10^–6 = 0,1 kg urán található.

M tömegű anyagban lévő urán atommagok száma:

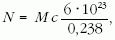
ahol c az urán koncentrációja. A tömeget kg-ban kell behelyettesíteni. Ennyi atommag aktivitása:

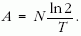
Itt T az urán felezési ideje másodpercekben. A feladatban csak a ²³⁸U-nal számolunk, a ²³⁵U-tól származó aktivitást elhanyagoljuk. A számadatok behelyettesítése után kapjuk: A = 1,23 · 10⁶ Bq. Ez több, mint 1 MBq!

Vizsgáljuk meg ennek a házban lakó emberekre gyakorolt hatását! Az urán bomlási sorában lévő elemek alfa- és béta-bomlásokkal bomlanak. Ezek a részecskék azonban - elektromosan töltöttek lévén - nagyon hamar elnyelődnek, ezért nem lépnek ki az építőanyagokból (vagy ha ki is lépnek a vakolat felső, vékony rétegéből, a levegőben nagyon kis út megtétele után elnyelődnek). A bent élő emberekre tehát ezek nem jelentenek veszélyt. Az emberekre tehát két forrásból származhat sugárterhelés:

• Az alfa- és béta-bomlásokat kísérő gamma-sugárzás egy része kiléphet a falból, és ez külső sugárterhelést okozhat.
• Másrészt az urán bomlási sorában lévő radon egy része kidiffundálhat a falból, mielőtt tovább bomlana, mivel nemesgáz. Ez a radon (és bomlástermékei) a levegővel együtt bekerülhetnek a tüdőbe, és ott belső sugárterhelést okozhatnak.

4. feladat (kitűzte: Sükösd Csaba)
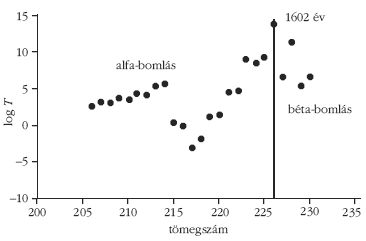
A rádium-izotópok felezési időit és domináns bomlásmódjaikat az alábbi ábra mutatja. (A függőleges tengely a ms-ban kifejezett felezési idők logaritmusát mutatja!) Az ábrán látható függőleges vonaltól (A = 226) jobbra a bomlások leggyakrabban béta-bomlással történnek, a függőleges vonaltól balra pedig alfa-bomlással.

Adjunk magyarázatot a megfigyelhető bomlási módokra, valamint minél több, a felezési időkben megfigyelhető viselkedésre!

Megoldás: Mivel mindegyik izotóp rádium, ezért Z = 88, azaz állandó. A megfigyelt változások tehát csak a neutronszám változására vezethetők vissza.

1. ) Az első megfigyelés az, hogy a legstabilabb rádium- izotóp a ²²⁶Ra. Ennek felezési ideje 1602 év. Itt van az energiavölgy mélypontja. Az ennél neutrondúsabb izotópok rendszámnövelő negatív béta-bomlásra hajlamosak, a neutronszegényebb izotópok pedig rendszámcsökkentő bomlásokat (például alfa-bomlás) mutatnak. És valóban, valamennyi A < 226 izotóp domináns bomlási módja béta-bomlás.
2. ) A következő megfigyelés az, hogy a rendszámcsökkentő (függőleges vonaltól balra eső) oldalon alfabomlásokat találunk, és nem pozitív béta-bomlásokat. Ennek oka az, hogy az alfa-bomlás - ha energetikailag lehetséges - akkor általában nagyobb valószínűséggel zajlik le, mint a pozitív béta-bomlás, hiszen a pozitív béta-bomlásban a gyenge kölcsönhatás játszik szerepet, míg az alfa-bomlásban az erős kölcsönhatás.
3. ) Egy további megfigyelés, hogy - egy érdekes kivételtől eltekintve, amelyre lentebb még visszatérünk - minél távolabb megyünk az energiavölgy mélypontjától, annál rövidebbek a mért felezési idők. Ez azzal magyarázható, hogy minél távolabb vagyunk a mélyponttól, annál meredekebb a "Pauli-lejtő", és ez egyre instabilabb atommagokat jelent.
4. ) A negyedik megfigyelés a völgy mélypontja közelében a felezési idők "váltakozása". Egy hosszú felezési időt egy rövid követ, majd megint egy hosszabbat találunk. Például a 226, 228, 230 tömegszámú izotópok felezési idői hosszabbak, mint a 227, 229 tömegszámú izotópoké, de hasonló váltakozást figyelhetünk meg a másik irányban is. Ennek oka a párenergiában keresendő. Mivel Z = 88, a protonszám páros. Emiatt páros tömegszám (A) esetén a neutronszám is páros, és ez stabilabb magot jelent. E nagyobb stabilitás megnyilvánulását látjuk a páros tömegszámú izotópok hosszabb felezési idejében.
5. ) Végül meg kell magyarázzuk azt, hogy A = 214 környékén miért találunk megint stabilabb magokat. Az A = 214 tömegszámú rádium atommagjában éppen N = 126 mágikus számú neutron található. Ez stabilizálja az ebben a tartományban lévő atommagokat, ezért emelkedik meg ismét a felezési idő az energiavölgy mélypontjától eléggé távol.

5. feladat (kitűzte: Radnóti Katalin)

1. ) Mekkora annak a fotonnak a hullámhossza, amelyiknek energiája egyenlő az elektron nyugalmi energiájával?

   Egy ilyen foton nyugvónak tekinthető elektronnal ütközik úgy, hogy az ütközés után eredeti terjedési irányával éppen ellenkező irányban fog mozogni.

2. ) Mekkora lesz a meglökött elektron sebessége?
3. ) Hányszorosára nő az elektron tömege?

Megoldás: A feladat feltétele szerint a foton kezdeti hullámhosszára:

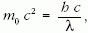
amiből

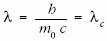
adódik. Itt λc az elektron Compton-hullámhossza. A Compton-szórt fotonok hullámhosszának megváltozására érvényes a következő összefüggés (lásd Függvénytáblázat):

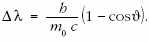
Esetünkben θ = 180°, így cosθ = –1, azaz

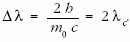
Tehát a visszaverődő foton hullámhossza háromszorosára nő, ezért frekvenciája - így energiája is - harmadára csökken. Tehát a foton energiájának 2/3-ad részét kapja meg az elektron, vagyis a teljes relativisztikus energiája,

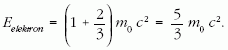
Az elektron tömege tehát 5/3-szorosára nő. Sebessége pedig:

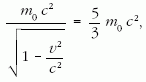
és innen

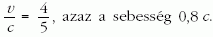
Az eredményre más gondolatmenettel is el lehetett, azaz a sebesség 0,8 c. jutni. A zsűri természetesen minden helyes levezetést maximális ponttal ismert el.

6. feladat (kitűzte: Kis Dániel)
A neutroncsillagok a legsűrűbb makroszkopikus anyagi objektumok az Univerzumban, felépítésük hasonlatos az atommagéhoz, azonban ebben az esetben - a magerők helyett a nagy tömeg miatt - a gravitáció tartja egyben az objektumot.

1. ) Számítsuk ki, mekkora az a minimális tömegszám, amelyre éppen kialakulhat kötött állapot, ha feltételezzük, hogy a neutroncsillag csak neutronból áll (Z = 0), és nagy tömegszám esetén a felületi tag elhanyagolható!
2. ) Mekkora az objektum minimális tömege?

   Útmutatás: bővítsük a Weizsäcker-féle energiaformulát egy, az objektum gravitációs energiáját figyelembe vevő taggal:

   

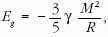
   ahol M az objektum tömege, R a sugara, és g a gravitációs állandó.

   Adatok: a neutron tömegét, a gravitációs állandó értékét, valamint a Weizsäcker-formula együtthatóit vegyük a Függvénytáblázatból!

   Megoldás: A gravitációs energiatag:

   

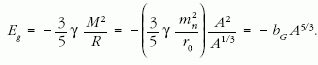
   Az ismert konstansokat beírva kapjuk: b_G ~ 9,3 · 10^–50 J. Írjuk fel a bővített Weiszäcker-formulát!

   

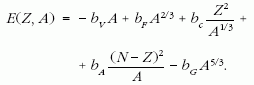
   Ha kihasználjuk az említett közelítéseket (Z = 0 és a felületi tag elhagyható), a képlet leegyszerűsödik:

   

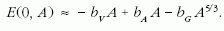
   A kötött állapot kialakulásának feltétele nyilvánvalóan E ≤ 0, ebből a tömegszámra kapunk egy összefüggést:

   

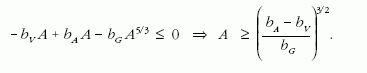
   A függvénytáblázat szerint b_A = 3,80 · 10^–12 J, b_V = 2,52 · 10^–12 J. Ezeket, valamint b_G fenti értékét beírva kapjuk: A ≥ 5,1 · 10⁵⁵. A neutroncsillag minimális tömege ennek alapján: M_N ≥ Am_n = 8,53 · 10²⁸ kg. Ez körülbelül egytizede a Nap tömegének.

   7. feladat (kitűzte: Kis Dániel)
   A speciális relativitáselmélet igazolása kapcsán gyakran hivatkoznak arra a kísérletre, hogy a Föld felszínén is mérhetőek a müonok. Az érvelés úgy szól, hogy az idődilatáció hatása nélkül a T = 2,2 · 10^–6 s felezési idejű részecskék elbomlanának mielőtt a légkörön áthaladnak, tehát nem mérhetnénk őket a felszínen. Vizsgáljuk meg az állítás helyességét! Mérések alapján (1963, Frisch és Smith) tudjuk, hogy a müonok átlagos sebessége v = 0,993 c (c = 299 793 km/s). Egy másik kísérletnél egy ballonban elhelyezett detektorral 10 000 m magasságban átlagosan 1448 müont mértek egy óra alatt.

   1. ) Mennyi müont mérhetnénk ugyanezzel a detektorral óránként a tengerszinten, ha (i) relativisztikusan, vagy (ii) nem-relativisztikusan kezeljük a problémát?
   2. ) Milyen következtetést vonhatunk le a számítási eredményekből? Hogyan kellene pontosítani a relativitáselmélet igazolására vonatkozó állítást?

   Megoldás: A relativisztikus számolások során szükségünk lesz a következőre:

   

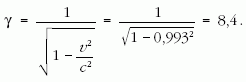
   A bomlás statisztikai folyamat, tehát a bomlási törvényből kell kiindulni:

   

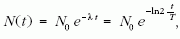
   ahol N₀ a 10 000 m magasan mért időegységenkénti (óránkénti) müonszám, és T a müon felezési ideje.

   A repülési idő Földhöz rögzített koordinátarendszerben

   

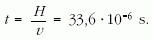
   Az (i) feladatban relativisztikusan kell számolnunk, azaz a repülési idő helyére a müon sajátidejét kell írnunk:

   

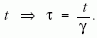
   Ebből

   

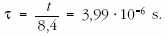
   A keresett beütésszám az adatok behelyettesítésével:

   

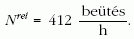
   Klasszikus számításhoz, a második esetben nem kell relativisztikus korrekció, így nem τ, hanem t behelyettesítésével kapjuk.

   

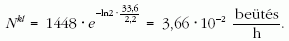
   Az eredményekből látható, abból a tényből, hogy müont detektálhatunk a tengerszinten, nem következik a relativitáselmélet igazolása. Hiszen a bomlás statisztikus jellege miatt idődilatáció nélkül is észlelhetünk müont, igaz átlagosan 27,3 óránként csak egyet! A pontos megfogalmazás az lenne, hogy a müon különböző magassági pontokban mért beütésszámai és az elméleti bomlásgörbe nem relativisztikusan számolva eltérnek egymástól, míg az idődilatációt figyelembe véve jól illeszkednek egymáshoz. Ez igazolja a relativitáselmélet helyességét.

   8. feladat (kitűzte: Radnóti Katalin)
   

   1. ) Határozzuk meg azt a küszöbenergiát, amely ahhoz szükséges, hogy egy proton-antiproton pár keletkezzen (az ütköző protonokon kívül), amikor egy felgyorsított proton álló protonba ütközik!
   2. ) Vajon, ha mindkét protont felgyorsítjuk azonos sebességre, és egymással szemben ütköznek úgy, hogy párt tudjanak kelteni, akkor a felgyorsított protonok összes energiája nagyobb, vagy kisebb kell legyen, mint az előző esetben? Indokoljuk meg állításunkat!

   Megoldás: A reakcióegyenlet a következő:

   

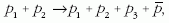
   ahol 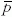az antiprotont jelöli.

   b )    Válasszunk először olyan vonatkoztatási rendszert, amelyben a tömegközéppont áll. Négy részecske van ekkor jelen. A küszöbenergiát akkor kapjuk meg, ha ezek a részecskék éppen csak létrejöttek, mozgási energiájuk nincs. Azaz a rendszer teljes energiája végállapotban E = 4m₀ c². Az energia megmaradása miatt az energiának a kezdeti állapotban is ekkorának kell lennie, csakhogy a kezdeti állapotban csupán két részecskénk van. Ebből következik, hogy mindkét részecskének m₀ c² mozgási energiával kell rendelkeznie. Egy ilyen - ütközőnyalábos - rendszerben összesen 2m₀ c² energiát kell befektetnünk.

   Kezdeti állapotban mindegyik proton teljes energiája tehát 2m₀ c², relativisztikus tömege pedig 2m₀. A protonok sebessége a

   

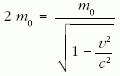
   összefüggésből:

   

   1. ) Most helyezkedjünk át a laboratóriumhoz rögzített vonatkoztatási rendszerbe! Határozzuk meg a p₁ proton sebességét abban a koordinátarendszerben, amelyben p₂ nyugalomban van!

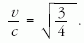
   Ez a koordinátarendszer nyilvánvalóan a p₂ proton sebességével mozog az előzőhöz képest. Ezért ebben a koordinátarendszerben - ha a Galilei-féle sebességösszeadás lenne érvényes - a p₁ proton kétszeres sebességgel kellene közeledjen az álló p₂-höz. Most azonban relativisztikus sebesség-összeadási szabályt kell használjunk, ezért:

   

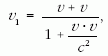
   mivel a koordinátarendszer is v sebességgel mozog, és az előző koordinátarendszerben a p₁ proton is v sebességgel mozgott. Ebből a fenti

   

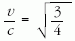
   behelyettesítéssel kapjuk:

   

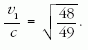
   A p₁ proton teljes energiája tehát:

   

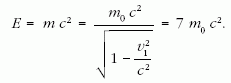
   Vagyis a proton teljes energiája 7m₀ c² lesz, azaz 6m₀ c² mozgási energiára kell felgyorsítani. Ez háromszor annyi, mint az ütköző nyalábok esetében befektetett teljes energia. Ekkor a proton a fénysebesség körülbelül 99%-ával mozog.

   9. feladat (kitűzte: Kis Dániel)
   Egy ütközőnyalábos gyorsítóban a következő reakció játszódik le: ²H+H → ³He+γ. Az ütköző részecskék teljes lendülete nulla (laboratóriumi rendszerben), összes mozgási energiájuk 0,1 MeV, a reakcióenergia pedig 5,5 MeV. Mekkora a reakcióban keletkezett hélium atommag mozgási energiája, ha a tömege m(³He) = 3,016029 m_u?

   Az m_u atomi tömegegység értékét vegyük a Függvénytáblázatból!

   Megoldás: Mivel a reakcióban a lendület megmaradó mennyiség, ezért a keletkezett részecskék teljes lendülete szintén nulla, azaz 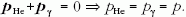. A végállapotban a termékek mozgási energiájának összege megegyezik az ütköző részecskék mozgási energiájának és a reakcióenergiának összegével, azaz E_összes = 5,6 MeV. A foton energiája E_γ = pc, a hélium atommag mozgási energiája

   

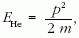
   így az energiamegmaradás:

   

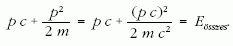
   A kapott összefüggés a pc szorzatra egy másodfokú egyenlet:

   

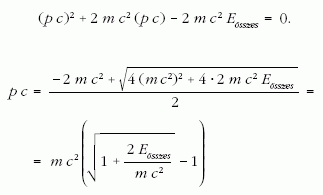
   A ³He nyugalmi energiája: mc² =2813,3141 MeV. Így már megoldható a pc-re vonatkozó egyenlet, mivel

   

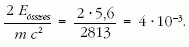
   Így kapjuk:

   

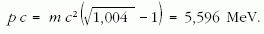
   A pc szorzat ismeretében egyszerű behelyettesítéssel megkapható a keresett mozgási energia:

   

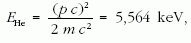
   azaz a végállapotban rendelkezésre álló energiának valamivel kevesebb, mint egy ezredrésze. Az energia legnagyobb részét a gamma-foton viszi el, mint azt vártuk is.

   10. feladat (kitűzte: Szűcs József)
   A ¹⁴C szénizotóp béta-bomlásánál 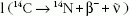a kirepülő β-részecske (elektron) energiája 0 ≤ E_β ≤ 0,155 MeV intervallumba eső értékeket vehet fel, mivel a bomlásnál felszabaduló energián a végállapotban lévő három részecske (a visszalökődő ¹⁴N mag, a kirepülő elektron és az antineutrínó) véletlenszerűen osztozik.

   1. ) Mekkora a visszalökődő ¹⁴N mag sebessége és mozgási energiája, ha a β-részecske mozgási energiája maximális?
   2. ) Mekkora sebességgel lökődik vissza a mag akkor, ha a β-részecske energiája nulla?

   Adatok: Az antineutrínó nyugalmi tömegét az elektronéhoz képest vehetjük zérusnak. Az ¹⁴N atommag tömegét vegyük kereken 14 m_u atomi tömegegységnek, a többi adatot vegyük a Függvénytáblázatból.

   Megoldás:

   1. ) Ha az elektron energiája maximális, akkor az antineutrínó sem energiát, sem lendületet nem visz el. Így a visszalökődő ¹⁴N mag lendülete, a lendület-megmaradás miatt megegyezik a nyugvónak tekintett ¹⁴C magból kirepülő elektron p_e = p_N lendületével.

      Az elektron lendületét a relativisztikus összefüggésből kaphatjuk meg:

      

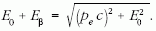
      Ebből az elektron lendülete:

      

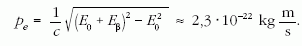
      Így a ¹⁴N mag visszalökődési sebessége:

      

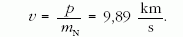
      A mag mozgási energiája pedig

      

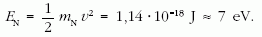
      A mag mozgási energiája körülbelül 4,5 · 10^–5-szerese az elektronénak, ezért úgy vehető, hogy a teljes bomlási energiát az elektron viszi el.

   2. ) Ha a β-rész mozgási energiája zérus, akkor lendülete is az, így jó közelítéssel a teljes felszabaduló energiát a keletkező antineutrínó viszi el és .

   Mivel a részecske nyugalmi tömegét zérusnak vehetjük, ezért az antineutrínó lendülete

   

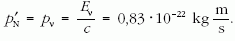
   Ebből a visszalökődő ¹⁴N mag sebessége:

   

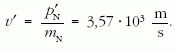
   Látható, hogy ekkor a mag sebessége körülbelül harmada az elektronon való visszalökődési sebességnek, így a mozgási energia még kisebb lesz (körülbelül 1/9-e) a korábbinak, tehát jogos volt a közelítés, hogy a teljes energia az antineutrínóra jut.

   Junior (II. Kategóriájú feladatok)

   8. feladat (kitűzte: Vastagh György)
   Tegyük fel, hogy van 5 db atomunk olyan anyagból, amelynek felezési ideje 3 perc. Mi a valószínűsége annak, hogy a következő 3 percben az 5 atom egyike sem bomlik el?

   Megoldás: A felezési idő alatt éppen 1/2 a valószínűsége annak, hogy egy atom elbomlik, és ugyancsak 1/2 a valószínűsége annak, hogy nem bomlik el. Az atomok egymástól függetlenül bomlanak (illetve nem bomlanak). Ezért annak a valószínűsége, hogy 5 atomból egy se bomoljon el:

   

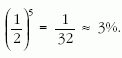
   9. feladat (kitűzte: Mester András)
   Radioaktív izotóppal gyilkolták meg 2006-ban A. Litvinyenko orosz ügynököt. Halálát (vélhetően az italával elfogyasztott) radioaktív polónium-210 okozta. Az izotóp igen aktív alfa-bomló, felezési ideje 139 nap. A földkéregben csak radioaktív bomlásból származó ²¹⁰Po van, amely az ²³⁸U bomlási sor tagja.

   1. ) Kinek a nevéhez fűződik az elem felfedezése?
   2. ) Milyen körülmények között veszélyes a , és miért mondják, hogy ellenőrzés esetén szinte lehetetlen kimutatni?
   3. ) Mennyi ²³⁸U aktivitása egyezik meg 1 milligramm ²¹⁰Po aktivitásával? (Az urán felezési ideje 4,5 · 10⁹ év.)
   4. ) Hány eV egy alfa-részecske energiája, ha 1 gramm tömegű ²¹⁰Po 140 watt teljesítményt szolgáltat?

   Megoldás:

   1. ) A polóniumot Maria Sklodowska és férje, Pierre Curie fedezték fel 1898-ban.
   2. ) Alfa-sugárzó lévén az elem csak a szervezetbe bejutva jelent veszélyt. A ²¹⁰Po a bomlási sor utolsó előtti eleme, nincsenek további radioaktív bomlástermékek. A ²¹⁰Po csak alfa-sugarakat bocsát ki, amelyek a szervezetből nem jönnek ki. Ezért sem a bomlástermékei révén, sem pedig a saját sugárzása révén nem árulja el magát, és így nagyon nehéz kimutatni.
   3. ) A ²¹⁰Po felezési ideje: T = 139 nap = 12 009 600 s. M tömegű ²¹⁰Po-ban lévő atommagok száma:

      

      

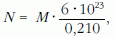
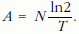
      A számadatokat behelyettesítve: A = 1,64 · 10¹¹ Bq.

      Az aktivitások egyezéséből kapjuk:

      

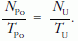
      Ebből

      

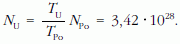
      Ennyi urán tömege:

      

   4. ) 1 gramm polónium aktivitása 1,64 · 10¹⁴ Bq, teljesítménye 140 W. Ebből egyetlen bomlásra jutó energia

      

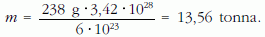
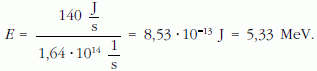
   Egy α-részecske energiája tehát körülbelül 5,33 MeV.

   10. feladat (kitűzte: Kis Dániel)
   Tekintsük a következő fúziós reakciókat: ²H+²H → n+³He és ²H+²H → p+³H, ezek röviden jelölése d(d,n)³He, illetve d(d,p)³H.

   1. ) Melyik reakció termel több energiát?
   2. ) A második reakcióban nem keletkezik radioaktivitást okozó neutron, ezért ha ezt használnánk, a termonukleáris erőmű alkatrészei nem aktiválódnának fel. Vajon mégis miért a ²H+³H → 4He+n, reakciót (D-T reakciót) kívánják az ITER-ben használni?

   Adatok: m(¹H) = 1,007825 m_u, m(²H) = 2,014102 m_u, m(³H) = 3,016049 m_u, m(³He) = 3,016029 m_u, m(n) = 1,008665 m_u, m(⁴He) = 4,0026 m_u, az m_u atomi tömegegység értékét vegyük a Függvénytáblázatból!

   Megoldás:

   1. ) A reakcióenergia a kezdeti és végállapotbeli magok nyugalmi energiakülönbségeként határozható meg: Q_He = 3,2744 MeV, illetve Q_H =4,0394 MeV. Az eredményekből következik, hogy mindkét reakció exoterm, így a nagyobb reakcióenergiájú folyamat, azaz a d(d, p)³H reakció termel több energiát.
   2. ) Két oka is van a D-T reakció használatának. Egyrészt a D-T reakció több energiát termel: Q_D-T = 17,6 MeV, másrészt pedig a d(d,p)³H reakció nem választható külön a d(d,n)³He reakciótól, mindkettő végbemenne bizonyos valószínűséggel. Tehát hiába alkalmaznánk tiszta deutériumból álló plazmát, a neutronoktól - és így az általuk létrehozott felaktiválódástól - így sem szabadulnánk meg.

   Számítógépes feladat

   A részecskegyorsítók egyik fontos típusa a lineáris részecskegyorsító. Ebben egy ionforrásból származó ionokat elektromos mezővel gyorsítjuk. A fémből készült, üreges gyorsító-elektródok (gyorsítóüregek) belsejében az elektromos térerősség nulla, a gyorsítás az elektródok közötti térben zajlik. Természetesen az egész gyorsítócsőben vákuum van, hogy a részecskék ne szóródjanak szét a levegő molekuláin. A gyorsítóüregekre periodikusan váltakozó feszültséget kapcsolunk. A gyorsítóüregek méretét, a közöttük lévő távolságot, a gyorsítófeszültség amplitúdóját és frekvenciáját úgy kell összehangolnunk, hogy az egyre gyorsuló részecskék az egymást követő gyorsítóüregek közé mindig megfelelő időpontban érkezzenek ahhoz, hogy ott tovább tudjanak gyorsulni.

   Fontos az is, hogy az ionforrásból csak a gyorsítófeszültség meghatározott időtartományában engedjünk be részecskéket a gyorsítóba. A "rossz" időpillanatokban beengedett részecskék össze-vissza bolyonganak a gyorsítóban, egyesek még visszafelé is tudnak gyorsulni.

   A lineáris gyorsítóból gyakran egy másik gyorsítóba "lövik be" a részecskéket (ez történik például a CERN-ben is). Ezért nagyon fontos, hogy az előállított részecskenyaláb energiája minél pontosabban a megadott értékű és minél kisebb szórású legyen, valamint az is, hogy a nyaláb időbeli szórása is kicsi legyen, azaz a nyalábban lévő részecskék a gyorsítási periódus jól meghatározott időpillanatában lépjenek ki a gyorsítóból.

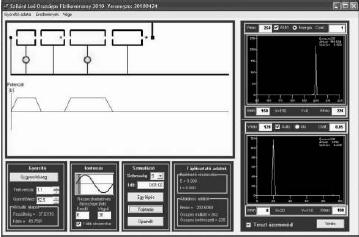
   A szimulációs feladatban egy lineáris gyorsítót kellett vizsgálni. A szimulált gyorsítón a fent említett valamennyi paramétert változtatni lehetett, és azok hatását meg lehetett figyelni. A versenyzők részletes leírást kaptak a program működéséről és használatáról.

   A feladat a következő volt: Állítsunk elő körülbelül 200 egységnyi energiájú részecskenyalábot 1 percen keresztül!

   A grafikonok alatt lévő "teszt üzemmód" kikapcsolása után indított szimuláció során már nem avatkozhatunk be a gyorsító paramétereibe. Az "Újraindítás" gomb megnyomása után a szimuláció elindul, és az 1 perc leteltével a szimuláció eredménye elmentésre kerül.

   Annál több pontot kap egy versenyző, minél

   • pontosabban megközelíti a 200 egységnyi energiát a nyaláb átlagértékével;
   • kisebb lesz a nyaláb energiájának a szórása;
   • kisebb lesz a nyaláb időbeli szórása;
   • nagyobb hányada jut a kibocsátott részecskéknek a céltárgyra;
   • több részecske érkezik a céltárgyra addig, amíg le nem jár a rendelkezésre álló idő.
   Az egyik versenyző által elért eredmény ábrája a következő oldalon látható.

   A képernyő jobb oldalán látható két grafikon mutatja a céltárgyra beérkező részecskék energia, illetve idő szerinti eloszlását. Látható, hogy a gyorsító megfelelő beállításával el lehet érni, hogy a részecskecsomagok energiájának elég kicsi legyen a szórása a kívánt érték körül, és hogy a részecskék a gyorsítófeszültség periódusidején belül egy eléggé jól meghatározott időpontban érjék el a céltárgyat (időben is lokalizálva legyenek).

   

   Kísérleti feladat

   Az elektron fajlagos töltésének meghatározása "varázsszem" (EM4 elektroncső) segítségével.

   A mérési elrendezés leírása: A méréshez használt elektroncsövet a régi, csöves rádiókban arra használták, hogy jelezze, hogy a rádió mennyire pontosan hangolódott rá egy adott állomásra.

   A varázsszem zölden világító kijelzője azt használja ki, hogy vannak olyan festékek, amelyek elektronok becsapódásakor fényt bocsátanak ki (lumineszkálnak). A gyorsan becsapódó elektronok folyamatos világítás érzetét keltik.

   A cső közepén hosszában húzódó fűtött katód szolgáltatja az elektronokat, ezeket az anódfeszültség (maximális értéke 250 V) gyorsítja. Az anód kiképzése olyan, hogy a felgyorsult elektronok egy része tovább tud haladni - immár állandó sebességgel - míg végül becsapódik az ernyőbe, ami a már említett festékkel van bevonva. Ahhoz, hogy az anód és az ernyő között ne változzon az elektronok sebessége, az ernyőnek az anóddal azonos potenciálon kell lenni.

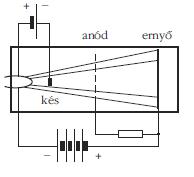   A csőben van még két eltérítő elektróda (ezeket késnek hívják), amelyek a keletkezett világító kép ("legyezők") szélességét határozzák meg. Ha az eltérítő elektródákra negatív feszültség jut, akkor taszítják a mellettük elhaladó elektronokat, megnő az árnyék területe. Ha kis feszültség kerül az eltérítő elektródákra, akkor nagy lesz a világító terület, kicsi az árnyék (a késfeszültség értéke 0 és –16 V között lehet).

   Az elektroncső "kiterített", lineárissá transzformált rajzát a mellékelt ábra mutatja.

   Az elektroncső adatai: fűtő feszültség: 6,3 V, anód feszültség: maximum 250 V, ernyő feszültség: maximum 250 V.

   Mérésünknél az elektronsugarat rá merőleges, homogén mágneses mezővel térítjük el. A mágneses mezőt 200 menetes, 3 cm hosszú, 3 cm belső átmérőjű tekerccsel állítjuk elő. Ezt a tekercset az elektroncsőre húzzuk úgy, hogy lehetőleg közös tengelyű legyen a tekercs és a cső.

   A tekercsben szabályozni és mérni tudjuk az átfolyó áramot, így a létrejött mágneses mező indukcióját meg tudjuk határozni. A mágneses mezőben az elektronsugár körpályára kényszerül. A körpálya sugarát megmérve határozhatjuk meg az elektron fajlagos töltését.

   Feladat: Mérje meg a tekercs több áramerősségénél (az áramerősség értéke ne legyen nagyobb 2 ampernél!), és többféle anódfeszültség (maximum 250 V) esetén az elektronsugár görbületét, és ebből adjon becslést az elektron fajlagos töltésére!

   Foglalja táblázatba a mért eredményeket, elemezze azokat! Térjen ki a mérési hibákra, becsülje meg azok értékét!

   Útmutatás: A méréshez használja a Program2010-et! Ezzel a webkamerát felhasználva képeket készíthet, és értékelheti a kapott képeket. Célszerű egy képet készíteni világosban az elrendezésről, ezt fel lehet használni a méretek kalibrálásához. A kalibrálás után magát a mérést feketével letakart csőről készített képeken célszerű elvégezni. Így a zavaró tükröződések kiküszöbölhetők.

   A kísérleti összeállításról készített fénykép alábbi kinagyított részletén jól látható a varázsszem elektronnyalábjának görbülete. A görbületi sugár megmérését a versenyzők számára rendelkezésre bocsátott program segítette. A program egy kört rajzolt az egérrel megadott három pontra, és a kör sugarát kijelezte pixelben. Kalibráció után a tényleges sugár ebből meghatározható volt, s ez lehetővé tette az e /m kiszámítását. A programmal azt is meg lehetett vizsgálni,

   

   hogy a webkamera mennyire merőlegesen nézett az elrendezésre, mert ellipszist is lehetett rajzoltatni négy megadott pontra. Megfelelő volt a beállítás, ha az ellipszis nagy- és kistengelyeinek hossza legfeljebb 1%-kal tért el egymástól.

   A kísérleti összeállítással az e /m arányra az irodalmi értéket 20-30%-ra megközelítő eredményt lehetett kapni.

   A verseny értékelése

   A verseny döntőjének délelőttjén a tíz elméleti feladat megoldására 3 óra, délután a számítógépes feladatra másfél óra, a kísérleti feladatra szintén másfél óra állt a versenyzők rendelkezésére. Egy-egy feladat teljes megoldása 5 pontot, a számítógépes feladat teljes megoldása 25 pontot, a kísérleti feladat teljes megoldása 25 pontot hozhatott. Maximálisan tehát 100 pontot lehetett szerezni. A legkiválóbb I. kategóriás versenyző 80 pontot ért el (tavaly 83 pont volt a legjobb eredmény). A legjobb junior versenyző fantasztikus 93 pontot ért el (tavaly 76 pont volt a legjobb). Az elméleti feladatok közül legnehezebbnek az I. kategóriás versenyzők 8. és 10. feladata bizonyult, ezekre a feladatokra 3 pont volt a legjobb eredmény. Az elméleti feladatok megoldásában Harstein Máté (Leőwey Klára Gimnázium, Pécs) I. kategóriás, valamint Szabó Attila (Leőwey Klára Gimnázium, Pécs) érték el a legjobb eredményt 38, illetve 49(!) pontot a maximális 50-ből. A Junior kategóriás Szabó Attila egyedül a II. kategóriás 9. feladaton veszített egyetlen pontot, azaz tökéletesen oldotta meg a "nagyokkal" közös feladatokat is!

   A mérési feladatra két versenyző érte el a maximális 25 pontot: Varga Ádám (SzTE Ságvári Endre Gyakorló Gimnázium, Szeged), valamint Harstein Máté. A számítógépes feladatra ebben az évben ketten kaptak maximális, 25 pontot: Havlik Tamás (Zrínyi Miklós Gimnázium, Zalaegerszeg) I. kategóriás és Farkas Martin (Vajda János Gimnázium, Keszthely) Junior kategóriás versenyző. Az összesített pontszámokban több helyen is holtverseny alakult ki. 2010-ben a következő diákok érték el a legjobb helyezéseket:

   I. kategória (11-12. osztályosok)

   I. helyezettek (80-80 ponttal): Harstein Máté, tanára Simon Péter, és Varga Ádám (80 pont), tanára Tóth Károly

   III. helyezett (70 pont): Kaposvári István, Hermann Ottó Gimnázium, Zalaegerszeg, tanárai Dezsőfi György és Dudás Imre

   "Junior" kategória:

   I. helyezett (93 pont): Szabó Attila, tanára Simon Péter

   II. helyezett (49 pont): Pölöskei Péter Zsolt, Batthyány Kázmér Gimnázium, Szigetszentmiklós, tanára Bülgözdy László

   III. helyezett (48 pont): Bolgár Dániel, Leőwey Klára Gimnázium, Pécs, tanára Simon Péter

   A záróülést és a díjátadást megtisztelte jelenlétével Süli János úr, a Paksi Atomerőmű Zrt. vezérigazgatója, Rónaky József, az Országos Atomenergia Hivatal főigazgatója, Kádár György, az Eötvös Loránd Fizikai Társulat főtitkára, Cserháti András, a Magyar Nukleáris Társaság elnökségi tagja, Horváth Miklós, az Országos Villamos Távvezeték Zrt. vezérigazgatója, Kiss István, a Paksi Atomerőmű Zrt. oktatási főosztályvezetője, valamint Radnóti Katalin főiskolai docens, a Women in Nuclear Magyarország (Magyar Nukleáris Társaság Nőtagozata) képviselője.

   Ebben az évben több különdíj átadására is sor került. A Magyar Nukleáris Társaság Nőtagozata és az Országos Atomenergia Hivatal az Országos Szilárd Leó Fizikaverseny döntője valamennyi résztvevőjének és a kísérőtanároknak ajándékul adta a Szemelvények a nukleáris tudomány történetéből című könyvet (Szerk. Vértes Attila). Az ajándékot - szimbolikusan - Rónaky József, az OAH főigazgatója adta át a résztvevőknek. Az Eötvös Loránd Fizikai Társulat egy-egy éves Fizikai Szemle előfizetést adott a két kategória első öt helyezettjének, amelyet Kádár György, az ELFT főtitkára adott át. A Magyar Nukleáris Társaság (MNT) képviseletében Cserháti András nyújtott át könyvjutalmakat a két kategória első öt helyezettjének. Az MNT egy további különdíját Kiss István a Paksi Atomerőmű Zrt. oktatási főosztályvezetője adta át Szabó Attilának az elméleti feladatok legjobb megoldásáért. Az MNT Nőtagozata (WIN) a két lányversenyzőt - különdíjként - meghívta egynapos látogatásra a Paksi Atomerőműbe. A látogatás célja az atomerőműben dolgozó, mérnöki beosztásban lévő nők munkájának megismerése volt. A különdíjat Radnóti Katalin, az MNT WIN budapesti alelnöke adta át.

   A záróülésen a tanulói díjak, különdíjak és oklevelek átadása után került sor az idei Delfin-díj átadására, amelyet minden évben a tanárok pontversenyében legjobb eredményt elért tanárnak ítél oda a versenybizottság. Ebben az évben a Delfin-díjat Pécsi István, a Verseghy Ferenc Gimnázium (Szolnok) tanára vehette át. Gratulálunk!

   A Marx György Vándordíj-at, amelyet minden évben a pontversenyben legkiválóbb eredményt elért iskolának ítél oda a Versenybizottság - idén a Leőwey Klára Gimnázium (Pécs) nyerte el. A Leőwey már 2008-ban is hazavihette egy évre a Marx György Vándordíjat. Gratulálunk!

   Az ünnepélyes eredményhirdetés végén Sükösd Csaba köszönetét fejezte ki a versenyt támogató Paksi Atomerőműnek - külön megemlítve a döntőt megelőző napon tett érdekes üzemlátogatást - és a paksi Energetikai Szakközépiskolának, valamint minden támogatónak és különdíjat felajánló szervezetnek a verseny megrendezésében nyújtott segítségükért.

   A versenyt 2011-ben is megrendezzük változatlan tematikával (lásd Fizikai Szemle 2010. decemberi szám). Ismételten bátorítjuk a határon túli magyar tannyelvu iskolák tanulóit is arra, hogy nevezzenek be az Országos Szilárd Leó Tanulmányi Versenyre. A nevezéseket a verseny http://www.szilardverseny.hu honlapjáról kiindulva lehet megtenni.

   ____________________

   1 Ezen a versenyen is, mint az elso Szilárd Versenyen (valamint 2004 óta ismét), a Junior kategória versenyfeladatai részben eltértek az I. kategória (11-12. osztályosok) feladataitól.