A VASNÁL NEHEZEBB ELEMEK KELETKEZÉSE CSILLAGOKBAN

Kiss Miklós
Berze Nagy János Gimnázium, Gyöngyös és
Debreceni Egyetem, Fizikai Tudományok Doktori Iskola

Izgalmas kérdéscsoport, hogy honnan származik a környezetünket és bennünket felépítő anyag, hol, mikor és hogyan keletkezett. Melyik elemből mennyi van, és miért pont annyi? Mai tudásunk szerint ezekre a kérdésekre meggyőző választ lehet adni: a csillagokban az energiatermelés forrása az atommagok fúziója, amelynek során könnyebb magok egyesülése révén nehezebb magok jöhetnek létre. A nehezebb magokban az egy nukleonra eső kötési energia a tömegszámmal együtt nő egészen a vasig, ezért a vasnál együttesen könnyebb két atommag összeolvadása erősebben kötött atommagot hozhat létre sugárzási energia kibocsátása mellett. Ez alapján még mindig nyitott kérdés, hogy hol és hogyan keletkeznek a vasnál nagyobb tömegszámú elemek.

Manapság már nemcsak a csillagbeli fúziós folyamatokról vannak részletes ismereteink, hanem a vason túlvezető neutronbefogásos folyamatokról is. Az ezekre alapuló elemkeletkezési modell alapjait Burbidge, Burbidge, Fowler és Hoyle (szokásos rövidítéssel B2FH) fektették le 1957-ben [1]. (Tudománytörténeti érdekesség, hogy munkájuk fő célkitűzése az állandó állapotú Világegyetemre vonatkozó elméleti modell "védelme" volt az akkoriban egyre inkább tért nyerő Ősrobbanással szemben, amiről azóta már tudjuk, hogy nem járt sikerrel.) A B²FH elképzelés lényege, hogy a vasnál nagyobb tömegszámú (vagy a szokásos, a címbeli kicsit pongyola szóhasználattal: a vasnál nehezebb) stabil elemek az úgynevezett asztrofizikai s-folyamat egyes lépéseiben keletkeznek. Az s-folyamat lényege, hogy a csillagban repkedő szabad neutronok befogásával egy stabil atommagból eggyel nagyobb tömegszámú instabil mag keletkezik, amely béta-bomlás során csakhamar eggyel nagyobb rendszámú stabil atommagba alakul át. A folyamat tehát a stabilitási völgy mentén húzódó s-úton lépked az egyre növekvő rendszámok felé. Az s betű az angol slow, azaz lassú szóra utal, ami azt jelzi, hogy a folyamat viszonylag lassan zajlik, mert a neutronok sűrűsége egy csillagban sok nagyságrenddel kisebb, mint a csillag életének végét jelző szupernóva-robbanásban, amelyet a nagy neutronsűrűség miatt a gyors neutronbefogással jellemzett r-folyamat kísér (r = rapid, azaz gyors). Az s-folyamatot elég jól értjük, segítségével a környezetünk elemgyakoriságát néhány százalékos pontossággal meg lehet jósolni. A részletekről azonban a közelmúltban is születtek meglepően új eredmények. Ilyenek például az úgynevezett aszimptotikus óriásági (Asymptotic Giant Branch, röviden AGB) csillagokban lezajló folyamatokról való új ismereteink, amelyek nemcsak a csillagok fejlődése szempontjából érdekesek, hanem az elemkeletkezés jelentős helyszínei lehetnek.

Írásunkban áttekintjük a nehéz elemek keletkezésének fizikai alapjait. A szokásos s-folyamat és r-folyamat mellett bemutatjuk saját modellünket [2] is, amely simán átvezet a két szélsőség között, bármilyen neutronsűrűség esetén alkalmazható.

Az elemek és atommagok rendszerezése

Manapság 118 elemet ismerünk, amelyek közül a Földön természetes módon 90 fordul elő. Az elem fajtáját az atommagjában található protonok száma határozza meg. Az izotóp fogalma közismert, az elemfogalomhoz kötődik. Az elemek relatív atomtömege nem egész szám, és ennek az az oka, hogy az adott elem atommagjában a Z darab proton mellett különböző mennyiségű neutron állhat. A természetben fellelhető anyag ezen izotópok keveréke. Így a relatív atomtömeg többnyire nem egész szám, mert egy elem izotópjainak keveréke, amelyek kémiai szempontból egyenértékűek. Az izotópok egy része stabil, vagy nagyon lassan bomlik. Az hidrogénnek két stabil izotópja (a prócium és a deutérium), valamint egy bomló izotópja (a trícium) közismert. Az ónnak (Z = 50) ugyanakkor tíz stabil izotópja van, míg a technéciumnak (Z = 43) és a prométiumnak (Z = 61) egy sincs. Ezért ismerünk csak kilencven természetes elemet és nem kilencvenkettőt. Az elemeket kémiai tulajdonságaik alapján Mengyelejev rendszerezte a jól ismert periódusos rendszerbe.

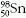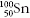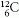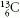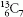Kevésbé közismert az atommagok táblázata [3]. Egy atommag Z db protonból és N db neutronból áll. Az izotóp azt jelenti, hogy Z = állandó (vízszintesen vannak egymás mellett az izotópok) például és vagy közismertebb példa és . Ha N = állandó, akkor a megfelelő magokra az izotón szót használjuk (függőlegesen egymás fölött) például és 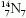. Itt a jelölést teljessé tettük a neutronok számának megadásával. Nincs stabil izotón N = 19, 35, 39, 45, 61, 71, 89 és 123 esetén. 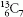Szokás még beszélni izobár magokról, ekkor a tömegszám, A = Z+N az állandó (a magok átlósan helyezkednek el) például és 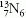. A negyedik lehetőség, amikor az N-Z mennyiség állandó (ez a másik 45°-os átló) nem kapott külön nevet, nincs különösebb jelentősége.

A magok tömegéből következtethetünk a mag kötési energiájára. A magok tömege ugyanis kisebb, mint az alkotórészek tömegének összege:

m(Z, N) = Z m_p N m_n - Δm.

A különbségből számolható a kötési energia az E = m c² összefüggést figyelembe véve, ha m helyére a tömeghiányt írjuk: E_k = Δm c².

Az egyes magokat jellemezhetjük azzal, hogy mennyi bennük az egy nukleonra (nukleon: proton, neutron) jutó kötési energia. Ehhez a kötési energiát kell osztanunk A-val, a tömegszámmal, ami éppen a nukleonok száma. Stabil magok esetére ennek nagyságát az 1. ábrán láthatjuk [4], amely mutatja, hogy mennyire kötöttek az egyes nukleonok. A maximumból látható, hogy átlagosan a vas 56-os izotópjának 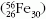nukleonjai vannak a legmélyebb energiájú állapotban. Az ábráról azt olvashatjuk, hogy könynyebb magok egyesítése energianyereséges egészen addig, amíg nem lépünk túl a vason (fúzió), illetve, hogy a nagyon nehéz magok kettébontása (maghasadás) is energianyereséges. Egy nehéz mag alkotórészeinek összes energiája csökkenhet, ha elbomlik, és így két mélyebben kötött mag jöhet létre.

Az elemek keletkezése szempontjából lényeges, hogy amíg a kötési energia negatív, addig az adott mag létezhet. Ha tehát az említett vas izotóphoz hozzáveszünk még egy neutront, akkor ott már az egy nukleonra eső kötési energia ugyan nem lesz minimális, de attól még az a mag létrejöhet. (Az ábrán a kötési energia nagysága látható, ez maximális, ha a kötési energia minimális.)

Az egyes izotópok naprendszerbeli gyakoriságát (hidrogén és hélium nélkül) a 2. ábra mutatja [4]. Az Ősrobbanáskor keletkező hidrogénből és héliumból a többi elemnél sokkal több van. A fő irány, hogy a gyakoriság a rendszámmal csökken, de az egyes elemek gyakorisága fűrészfogszerűen ingadozik, és van né- atommagok relatív gyakorisága, Si = 1 hány elem, amely kilóg a sorból. Némelyikből kevés van (lítium, berillium, bór), másokból sok (vas, platina, ólom), legalábbis az ábra fő irányát alapul véve.

Csillagfejlődés

A csillagok rendszerezhetők, ha fényességük és felszíni hőmérsékletük alapján ábrázoljuk őket. Így kapjuk a Hertzsprung-Russell-diagramot (HRD, 3. ábra), amelyben a csillagok elsődlegesen három területen helyezkednek el: a fősorozaton, felette jobbra a vörös óriások, alatta balra a fehér törpék. Egyes csillagok fényesebbek és vörösebbek, ugyanakkor hidegebbek, mások halványabbak, kékebbek és forróbbak, mint a fősorozatbeliek. A HRD egy pillanatfelvétel a csillagok állapotáról. Ha egy területen sok csillag látható, az azt jelenti, hogy adott pillanatban, ebben a fejlődési állapotban sok csillag van, vagyis ez az állapot hosszú ideig tart. Láthatóan a fősorozaton, valamint a vörös óriás állapotban van a legtöbb csillag.

Az elemek keletkezése az Ősrobbanás után kezdődik, az úgynevezett elsődleges atommag-keletkezéssel, amikor kialakul a hidrogén és a hélium, pontosabban a hélium egy része. A történet a csillagokban folytatódik. A bennük zajló energiatermelő folyamatok során felépülnek az elemek a hidrogéntől lényegében a vasig.

A csillagok fejlődése a gravitációs összehúzódással keletkező anyagmennyiség tömegén múlik. Az összehúzódó anyag főleg hidrogénból és héliumból áll, de a keletkezés időpontjában már korábbi csillagfejlődésben keletkezett anyag is bekerülhet a gázfelhőbe. A héliumnál nehezebb elemeket asztrofizikai szóhasználattal egyszerűen fémnek (metálnak) nevezzük. Hogy ezekből mennyit tartalmaz a csillag, a fémesség (metallicitás) fogalmával jellemezzük.

Az elemkeletkezéssel kapcsolatos legfontosabb csillagfejlődési lehetőségeket az 1. táblázatban fog- laljuk össze. A nehéz elemek keletkezése jellemzően a napnál nagyobb tömegű csillagokban lehetséges, ezért részletesebben csak ezekkel foglalkozunk. A csillagok fejlődési üteme tömegfüggő: minél nagyobb a tömegük, annál gyorsabbak a folyamatok. A Napnál sokkal nehezebb csillagok életideje néhány tízmillió év.

A HRD fősorozatán levő csillagok p-p ciklusának első lépésében két protonból egy deuteron keletkezik. Eközben az egyik protonnak pozitív béta-bomlással neutronná kell alakulnia, aminek valószínűsége kicsi, ezért ez a folyamat lassú. A csillagok emiatt a fősorozaton teljes élettartamukhoz képest sokáig tartózkodnak. A hidrogénégető csillagok a fősorozaton tartózkodnak egészen addig, amíg a hidrogénátalakulás a csillag magjában zajlik. Ezután a hidrogén a mag körüli héj mentén alakul át, a csillag vörös óriássá válik. A 80-as évek kutatási eredményei alapján a csillag fejlődése, ha a tömege 0,8-8M_Θ tartományba esik, a vörös óriás állapot után az aszimptotikus óriáságon (AGB) folytatódik. Az elnevezést a HRD-n való elhelyezkedésük indokolja. A 4. ábrán egy 5M tömegű csillag vándorlása látható a HRD-n [5]. (A T_eff effektív hőmérsékletet a csillagfelszín hőmérsékletének jellemzésére használják. A csillaggal megegyező sugarú és luminozitású fekete test hőmérsékletét értjük rajta.)

Az AGB csillagok magjuk héliumkészletének kimerülése után érdekes fejlődést mutatnak. A mag ekkor szénből és oxigénből áll. A csillag a mag körüli vékony héjban héliumot éget, egy külső héjon hidrogént. A rövid héliumégési szakasz (thermal pulse, TP) után a héjak közötti tartomány felkeveredik a külső hidrogénburokba (TDU = third dredge up). Ezt egy hosszabb, nyugodt hidrogénégető szakasz követi a külső héjon (IP = interpulse). A TPAGB állapot a 4. ábrán a 15. pontnál kezdődik. A hélium-, illetve hidrogénhéj-égések, a TP, TDU, IP felváltva követik egymást, a csillag tömegétől függően tízszer-százszor [4, 5].

Nyolc naptömegtől kezdve várható további fejlődés. A felmelegedő magban további fúziós folyamatok következnek be. Tizenegy naptömegtől kezdve, ha a visszamaradó mag tömege meghaladja a Chandrasekhar-határt (= 1,4 naptömeg), a magegyesülési folyamatok tovább folytatódnak: két szénből neon, nátrium, magnézium keletkezhet. E folyamatok egészen a nikkelig 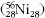vezetnek, ami vassá bomlik le 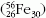. Miután a csillag fejlődése eljut eddig a pontig, megszűnik a fúziós energiatermelés további lehetősége, a csillag összeomlik, és szupernóvává válik (SN II). A robbanás következtében vasnál nehezebb elemek is létrejönnek.

A szupernóváknak másik fajtája (SN Ia) olyan fehér törpe és vörös óriás komponensekből álló kettőscsillagoknál alakul ki, ahol elegendő a fehér törpe tömege (nagyobb, mint a Chandrasekhar-határ). Ezeknél anyag áramlik át a vörös óriásról a fehér törpére, és ez vezet a robbanásszerű átalakuláshoz. Itt az elemek a vasig elmaradt fejlődést folytatják, vasnál nehezebb elemek nem jönnek létre.

Túl a vason

A vason túl fúzióval már nem keletkeznek magok (legfeljebb protonbefogással), az építkezés fő lehetősége a neutronbefogás. Fontos kiemelni, ami B²FH eredeti cikkében is szerepel, hogy a neutronbefogás könnyebb magok esetén is lehetséges folyamat, tehát már a vas előtt is. Ehhez csak az kell, hogy valamelyik neutrontermelő folyamat működésben legyen. Az egyes csillagok színképében megfigyelt technécium, amelynek nincs stabil izotópja, tehát ott keletkezik neutronbefogással.

A klasszikus megközelítés

Két mennyiség egyértelműen jellemzi a magokat: a protonok száma (Z), és a neutronok száma (N). Az s-folyamatban csak a kettő összegével, a tömegszámmal (A) jellemezzük a stabil atommagokat. A folyamat két fő lépése a neutronbefogás és a béta-bomlás.

Neutronbefogásnál eggyel nő a neutronok száma. Ha a keletkező mag stabil, újabb neutront foghat be, ha nem stabil és béta-bomlással elbomlik, akkor a rendszám eggyel növekszik. Csak neutronbefogással egyet jobbra, a két folyamattal együtt egyet felfelé léphetünk az elemek létráján (5. ábra).

Ez a két folyamatból álló lépés megismétlődhet, a folyamat folytatódhat, amíg a keletkező új elem stabil. Az s-folyamat során tehát egy adott A tömegszámú mag mennyisége (N_A) két ok miatt változik: (1) az A-1 tömegszámú atommag egy neutront befog, (2) az A tömegszámú atommag egy neutront befog (akár stabil, akár nem a neutronbefogással keletkező új mag):

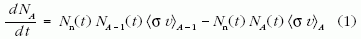
ahol N_n a neutronok sűrűsége, 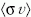a sebességre átlagolt befogási hatáskeresztmetszet. Bevezetve a λ_n = N_n 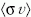jelölést, az (1) egyenlet a

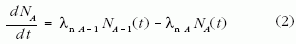
alakban írható (τn = 1/λ_n a mag keletkezésétől a neutronbefogásig eltelt átlagos idő). Az összes magot figyelembe véve (2) egy csatolt differenciálegyenlet-rendszert jelent, amelyet minden magra egyszerre kell megoldani [6].

Az s-folyamat akkor lehetséges, ha a neutronok sűrűsége nem túl nagy, és így a neutronbefogással keletkező új, béta-bomló mag újabb neutronbefogás előtt bomlik, azaz a béta-bomlás ideje sokkal kisebb a befogási időnél (2. táblázat). Ha a nagy neutronsűrűség következtében a béta-bomlást újabb többszörös neutronbefogás előzi meg, akkor a folyamat gyors, azaz r-folyamat.

Érdemes a Z-N síkon áttekinteni a folyamatokat (6. ábra). A lassú folyamat a stabil magok közelében halad - a béta stabilitás völgyében, a gyors pedig a völgytől jobbra, a neutrondús magok mentén. A távolodás csak a kis befogási hatáskeresztmetszetű magokon akad el a telített neutronhéjú magoknál, az úgynevezett mágikus számoknál: 50, 82, 126. A lassú folyamat a bizmutnál 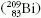véget ér. Az urán pedig csak gyors folyamatban keletkezik.

A vasnál nehezebb elemek gyakoriságának mintegy felét az s-folyamatnak köszönhetjük a Tejútrendszerben [4, 7].

Elemek keletkezésének modellezése közelítő feltevések nélkül

Az előbbi részben ismertetett B²FH-féle osztályozás érthető és célszerű, mert analitikus megoldást lehet találni. Ami meglepő, hogy ez az értelmezés nem finomult az irodalomban napjainkig (2010) [8, 9], annak ellenére, hogy a mai számítógépekkel az egyszerűsítő feltevések nélkül kapható differenciálegyenlet-rendszer is megoldható. Az s-folyamat, r-folyamat felosztás 1957-ben nagyon célszerű volt, és ma is hasznos, ha mint határesetekre tekintünk az egyes magok keletkezésével kapcsolatban.

Ha a konkrét neutronbefogási lehetőségeket tekintjük, akkor a magok nagy számából adódó egyensúlyi koncentrációt kell tekintenünk, vagyis a statisztikus megközelítést [2]. Hogy ez célszerű, arra jó példa a 3α folyamat első lépése: a szinte azonnal kettéváló berillium egyensúlyi koncentrációjának köszönhetően jöhet létre a szén . Ehhez hasonlóan a csillagokban bekövetkező neutronbefogást nem csak a stabil, vagy hosszú életű magokban követheti újabb. A magok egy része akkor is befog újabb neutront, ha a béta-bomlás gyors. A magok nagy része elbomlik, ahogy a B²FH cikkben, és azóta még sokszor leírták. Ugyanakkor valamennyi mag bármilyen rövid felezés mellett befoghat újabb neutront, és ilyen befogások meg is történnek. Ennek jelentősége mennyiségileg természetesen a csillagbeli körülményektől és az egyes magok átlagos élettartamától függően változik. A csillagbeli körülmények jellemzése szempontjából fontos tényezők a fémesség és a neutrontermelés.

A Nap összetételéről tudjuk, hogy tömegarányban 70% hidrogén, 28% hélium, és 2% fém (nehezebb elem) [9]. Az utóbbiak csak úgy kerülhettek bele, hogy életciklusukon végigjutott csillagokban keletkeztek. Erre az Ősrobbanás óta elegendő idő állt rendelkezésre. Ebből az következik, hogy a csillagok jelentős részében jelen van a vas is, és más nehezebb elemek. Így, ha a neutronforrások kinyílnak, lehetségessé válik a neutronbefogás.

A neutrontermelés a csillagok héliumégetési szaka- befogási hatáskeresztmetszet = 30 KeV-en (mb) kT szától kezdve folyamatos. A két fő neutrontermelő folyamat: 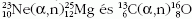. Az első folyamat nagy tömegű, héliumégető csillagoknál, illetve AGB csillagok TP-állapotánál van jelen, míg a második AGB csillagoknál a TP-t követő felkeveredés - TDU - után áll rendelkezésre.

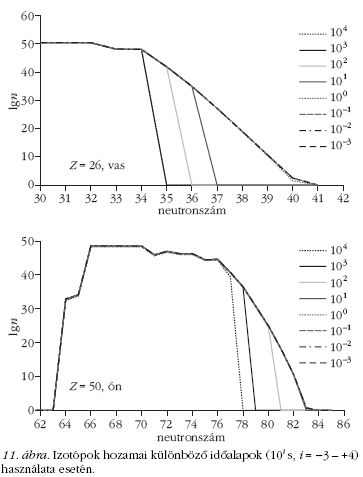
A különböző csillagokban található neutronsűrűségek [7]: vörös óriásban N_n ~ 10⁷-10⁸ cm^-3, AGB csillag termális pulzusában N_n ~ 10¹⁰-10¹⁴ cm^-3, szupernóvában N_n ~ 10²⁰-10²⁵ cm^-3. A neutronbefogási időtartamot befolyásolják még a befogási hatáskeresztmetszetek, amelyeknek a magok neutronszámától való függésének fő jellegzetességei a 7. ábrán láthatók [6].

Tekintsünk tehát minden olyan átalakulást, amely egy adott mag mennyiségét megváltoztatja: béta-bomlással érkezni is lehet egy magba, de az alfa-bomlás is növelheti és csökkentheti a magok számát. Ez a kiindulási lehetőség már Clayton alapművében benne van [10], azonban klasszikus s-folyamatokra nem használható ki. További lehetséges folyamatok: elektronbefogás, pozitív béta-bomlás, alfa-bomlás, protonkibocsátás, kettős bétabomlás (negatív vagy pozitív), spontán hasadás (8. ábra). Ezek az átalakulások többnyire jelentéktelenek, noha bizonyos magoknál jelentősek is lehetnek.

Az összes folyamatot tartalmazó teljes átalakulási egyenlet kezdete:

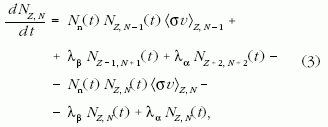
ahol a paraméterek értékei az adott (Z,N)-magra vonatkoznak. Az egyenletet még folytatni lehet a többi folyamattal. Ha pontos számítást szeretnénk, akkor minden lehetőséget figyelembe kell vennünk. Meghagyjuk a rendszernek adott körülmények között a saját fejlődés lehetőségét, azaz egy magról tetszőleges irányba lehetnek elágazások. A csatolt differenciálegyenlet- rendszer megoldása számítógéppel lehetséges. Válasszunk egy időalapot (τ). Nézzük, hogy ezalatt hány és milyen átalakulás következik be. Induljunk ki csak vasból, de kövessük az összes mag hozamának változását, és használjuk a két lépést váltakozva.

1. lépés: neutronbefogás. Egy közbülső helyen tároljuk a τ időtartam alatt átalakuló magokat, a maradékot természetesen meghagyva a helyén, majd az átalakult magokat hozzáadjuk a megfelelő új helyhez (készletezés).

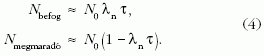
A használt elsőrendű közelítés érvényes, ha λ_n << 1, ami τ = 1 s időalapot és a csillagokban jellemző paramétereket, kT = 30 keV, σ = 100 mb feltételezve mintegy N_n = 10¹⁵ cm^-3 neutronsűrűségig jól teljesül, λ_n = 2,5 · 10^-17N_n cm³/s.

2. lépés: bomlás. Most a magokat a rájuk jellemző, τ időtartam alatt bekövetkező bomlásnak megfelelően készletezzük, megint minden magnál a rá jellemző adatokat használjuk. Először áttöltjük az átalakult magokat, megőrizve azokat, amelyek megmaradtak, azután a célhelyre mindegyiket hozzáadjuk. Ezeket a lépéseket a mag felezési ideje (T = ln2/λ) és a bomlási arányok alapján megtehetjük. Mivel véges időalappal dolgozunk, át kell gondolnunk, hogy a felezési idők hosszának megfelelően hogyan járjunk el. A használt három eset a következő. Ha a felezési idő közepes, akkor a pontos bomlási törvényt használjuk:

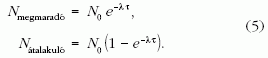
(Az alkalmazás pontos feltétele, hogy 0,01 < exp(-λτ) < 0,99, ami τ = 1 s lépésközt alkalmazva: a felezési

időre a 0,15 s < T < 69 s tartományt jelenti. Egy másodperces lépésköz esetén, ha T > 69 s, akkor az elsőrendű közelítést használjuk,

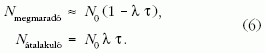
Ha pedig T < 0,15 s: feltesszük, hogy minden részecske elbomlik.

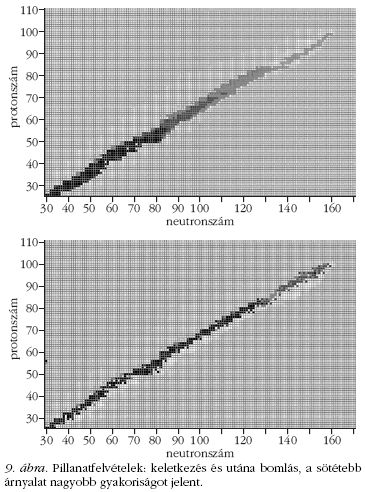
Ahhoz, hogy a számolást ténylegesen elvégezhessük, szükség van az egyes magokat jellemző neutronbefogási és bomlási adatokra. Ez elég sok adat, főként, ha figyelembe vesszük, hogy magonként legalább kettő (stabil magok esetén a stabilság jelölése és a befogási hatáskeresztmetszet, σ), de esetleg öt adat (felezési idő, egyik és másik bomlási mód, elágazási arány, σ) is szükséges lehet. A figyelembe vett 2096 magra mintegy 10 500 adatot használunk [2]. Az elemek keletkezésének követése grafikus felülettel nagyon látványos. Láthatjuk az épülést és az azt követő bomlást is (9. ábra).

Ha a bomlásnál hosszabb időt várunk, néhány elem - azok, amelyeknek nincs stabil izotópja, például a technécium - el is tűnik. (A 43. elem az s-folyamat észlelési bizonyítéka.) Ugyanakkor a folyamatokat célzottan is vizsgálhatjuk, elemezhetjük. Ezeket itt nem soroljuk fel, csak néhány tapasztalatról írunk.

1. 1090 mag keletkezik normál s-folyamatra jellemző neutronsűrűséget (N_n = 10⁸ cm^-3) alkalmazva.
2. A program időalapja jelentős hatással van a futásra. A fejlődés mindig sávos. A sáv szélességét a számítás időalapja befolyásolja. Azonban τ-nak fizikai tartalma nincs, csupán számolási paraméter. Az időalaptól függő sávok a 10. ábrán láthatók. A futások összesen ugyanannyi fizikai ideig tartottak. Látható, hogy ha nagy időalappal számolunk, keskeny sávban, szinte a béta-stabilitás völgyében halad a folyamat. Ha rövid időalapot választunk, a sáv kiszélesedik. A kép árnyalásához a 11. ábrán a vas és az ón izotópjainak gyakorisági profilját láthatjuk. A logaritmikus skála lehetővé teszi, hogy az eltérő nagyságrendek ellenére minden izotóp mennyisége láthatóan megjelenjen.

   

   Adott pillanatban bomlékony izotópokból nagyon kevés van, de hosszú idő alatt ezeken keresztül sok mag alakul át. Az ábrák pillanatfelvételek, és az egyensúlyi koncentrációkat mutatják. Például a vasnál, ha N = 38, akkor minden másodpercben mintegy 10²⁰ db 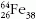izotóp van, ami nagyon kevés (10 µg). Ha a tekintett idő ezer év, tehát nagyjából 3,1 · 10¹⁰ s, akkor 1,1 · 10³⁰ db magátalakulás történik ezen az átalakulási csatornán, ami azért is érdekes, mert elvileg azt gondolnánk, hogy a 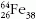nem is létezik. Nagyobb neutronsűrűség (N_n > 10⁸ cm^-3) esetén a hozzájárulás még jelentősebb.

3. A neutronsűrűség és így a neutronfluxus már fizikai körülmény. A nagy fluxus nagyon kiszélesíti a fejlődési sávot (képszerűen "erős neutronszél messze elfújja a magokat a völgyből") a nagy neutronszámú magok felé. A 12. ábrán más is látható. Bejelöltük a stabil magokat, kiemelve a hagyományos megközelítés szerinti keletkezési módjukat: s-mag, r-mag, p-mag. Például az s-mag onnan kapta nevét, hogy csak s-folyamatban keletkezik, mert egy stabil mag leárnyékolja az r-folyamatban való keletkezés elől. Az s- és az r-magok többnyire párba állíthatók, például ¹³²Te-¹³²Xe, ¹⁵²Sm-¹⁵²Gd, ¹⁹²Os-¹⁹²Pt.

4. A programmal a neutronsűrűséget változtatva vizsgálhatjuk, mennyi lesz az r-magok és az s-magok mennyiségének aránya: R. A 13. ábrán a modellben jósolt R és a Naprendszerben észlelt arány hányadosát ábrázoljuk a neutronsűrűséggel arányos neutronfluxus függvényében. A legtöbb pár gyakoriságaránya a megfigyelt értékhez viszonylag közelinek adódik N_n = 10¹⁰ cm^-3 neutronsűrűség esetén.
5. A klasszikus s-folyamat a polónium gyors alfabomlása miatt a bizmutnál véget ér (14. ábra). Ahogy a polónium keletkezik, rögtön el is bomlik, így gátat szab a további elemkeletkezésnek. Amennyiben a neutronsűrűséget egy küszöbnél nagyobbnak választjuk, N_n ≥ 10¹⁰ cm^-3, akkor a széles sáv miatt elkerülhető a polónium csapdája, ha van elég idő a fejlődésre. A fejlődésnek ebben az esetben csak a fermium spontán hasadása vet véget. Az AGB csillagokban a termális pulzusok alatt van ilyen körülmény [5, 7].
6. A fejlődés és a sávszélesség szempontjából további fontos paraméter, hogy mennyi vas áll rendelkezésre a neutronbefogási folyamat kezdetén. E paraméterre a csillagtömeg és a fémesség alapján következtethetünk.
7. A számítások nagyon függenek a befogási hatáskeresztmetszetektől, amelyek Z = 83-ig (bizmut) állnak rendelkezésre. A bizmutnál nehezebb elemek esetén csak kevés adat van. Korszerű kutatások eredményeként egyre több és pontosabb neutronbefogási hatáskeresztmetszet és atommagbomlási adat áll rendelkezésre, ezért a modellszámítás eredménye folyamatosan javítható.

Összegzés

Az itt leírtak alapján a csillagokbeli elemkeletkezés a stabilitási völgy mentén húzódó széles sávban történik, amelynek leírására egyszerű fizikai alapokon nyugvó modellt - nevezhetnénk sáv-modellnek (band-process, b-process = b-folyamat ) - javasoltunk. Modellünk alapján azt is meg tudjuk mondani, hogy a klasszikus s-folyamat akkor látható a sávmodell alapján, ha nagyon nagy az időalap (τ > 10⁴ s). Ha azonban rövid (1 s, vagy rövidebb) időalapot használunk, határozottan széles a sáv még kisebb neutronsűrűség esetén is. (A nagyon rövid időalap ára a nagyon hosszú számítási idő.) Mondhatjuk, hogy valójában az s-folyamat a b-folyamat idealizált széle.

A hagyományos megközelítés hiányossága, hogy bizonyos feltevésekkel (a felezési idő sokkal kisebb, mint a befogási idő) a magok jelentős részét kizárja a fejlődésből. Ha azonban az s-folyamaton a kis neutronsűrűség mellett bekövetkező neutronbefogási folyamatot értjük (N_n ~ 10⁷ - 10⁸ cm^-3), és r-folyamaton a nagy (N_n ~ 10²⁰-10²⁵ cm^-3) neutronsűrűség mellett bekövetkező neutronbefogási folyamatot, akkor értelmezni kell a köztes sűrűségen, N_n ~ 10¹⁰-10¹⁴ cm^-3-en lehetséges folyamatot is. Az utóbbiak jellemző helyszínei az AGB csillagok TP állapota [5].

Modellünkben, a differenciálegyenletekben az egyes magokat mind a rendszám, mind a neutronszám szerint megkülönböztetjük, nem korlátozzuk a neutronsűrűség lehetséges értékét. Az elemkeletkezést a felezési idő, a hatáskeresztmetszet, a neutronsűrűség és az adott magot szülő mag mennyisége (átlépési küszöb) határozza meg.

A modell ellenőrzésére több lehetőség van. A már említett r- és s-magpárok aránya mellett főként a gyakoriságok reprodukálása jelentheti a modell jóságát. Utóbbi azonban sok más paramétertől is függ, hiszen az elemek különböző állapotú csillagokban, eltérő körülmények között keletkeznek.

Irodalom

1. Burbidge M. E., Burbidge G. R., Fowler W. A., Hoyle F.: Synthesis of the elements in stars. Rev. Mod. Phys. 29 (1957) 547.
2. Kiss M., Trócsányi Z.: A unified model for nucleosynthesis of heavy elements in stars. Journal of Physics: Conference Series 202 (2010) 012024
3. http://ie.lbl.gov/toips/greatch.pdf/
   http://ie.lbl.gov/toi/pdf/chart.pdf/
   http://nucleardata.nuclear.lu.se/NuclearData/toi/pdf/chart.pdf
4. Jeffery C. S.: Stellar Structure and Evolution: an Introduction. In Principles and Perspectives in Cosmochemistry. Goswami A., Reddy B. E. (editors), Springer 2010.
5. Habing H. J., Olofsson H.: Asymptotic Giant Branch Stars. Springer, 2004.
6. Rolfs C. E., Rodney W. S.: Cauldrons in the Cosmos. The Univ. of Chicago Press, 1988.
7. Lugaro M., Karakas A. I., Bisterzo S.: Models and observations of the s process in AGB stars. NIC X, Mackinac Island, Michigan, USA, 2008.
8. Käpeller F., Beer H., Wisshak K.: S-process nucleosynthesis - nuclear physics and the classical model. Rep. Prog. Phys. 52 (1989) 945-1013.
9. Pagel B. E. J.: Nucleosynthesis and Chemical Evolution of Galaxies. Cambridge University Press, 2009.
10. Clayton D. D.: Principles of Stellar Evolution and Nucleosynthesis. Univ. of Chicago Press, 1968, 1983.
11. Tuli J. K.: Nuclear Wallet Cards 2005. Brookhaven National Laboratory

______________________________

Köszönöm Trócsányi Zoltánnak a cikk gondos áttanulmányozását, tartalmának és formájának kialakításához adott hasznos ötleteit, tanácsait, segítségét