Fizikai Szemle honlap |
Tartalomjegyzék |
Bokor Nándor
BME Fizika Tanszék
Ebben a cikkben olyan járművet nevezek rakétának, amely állandó ütemben, magához képest állandó u sebességgel hajtógázt bocsát ki hátrafelé, és így hajtja magát előre. Egy rakéta akkor relativisztikus, ha a sebességek - a hajtógázé vagy a rakétáé vagy mindkettőé - a fénysebességgel összemérhetőek. (A cikkben végig c = 1 egységeket használok [1]. A sebességek ennek megfelelően dimenzió nélküli számok, amelyek csak (-1) és 1 közötti értékeket vehetnek fel; a tömeg, impulzus és energia pedig ugyanabban az egységben mérendő.)
A gyorsítási folyamat során a rakéta tömege folytonos ütemben csökken (hiszen hajtógáz formájában tömeget lövell ki). Az alapprobléma: meghatározni a rakéta végsebességét adott kezdeti/végső tömegarány mellett. A probléma szokásos tárgyalásmódjában a gyorsítási folyamatot "időben visszafelé lejátszott rugalmatlan ütközések sorozataként" fogjuk fel. Minden kis "rugalmatlan ütközési" fázisban a rakéta kis sebességnövekményre tesz szert. Gondosan végzett összegzéssel - azaz integrálással - kapható meg a végsebesség [2].
Szemléltető erejénél fogva egy jó ábra gyakran sokkal jobban fejleszti fizikai intuíciónkat, mint egy hosszadalmas, tisztán algebrai számolás. Milyen szemléltetőeszközt nyújthat a rakétaprobléma tárgyalásához az ütközések elemzésénél már hasznosnak bizonyult energia-impulzus diagram [1]? Hogyan lehet a rakéta gyorsuló mozgását ábrázolni egy ilyen diagramon?
Nézzük az 1. ábrát! Az mk kezdeti tömeggel rendelkező, nyugalomban levő rakéta éppen elindul. Az első kis adag hajtógáz (amelynek energia-impulzus vektora a kis felső vektor) kilövellése által a rakéta tömege kicsit csökken (energia-impulzus vektora egy kisebb m értékű hiperbolára illeszkedik, ahogy az ábrán látható), és kis sebességnövekményre tesz szert (energia-impulzus vektora kicsit bedől az E-tengelyhez képest).
A 2. ábra a folyamat egy későbbi lépését ábrázolja. A rakéta ekkor már jóval kisebb tömegű (ezt megint abból lehet látni, hogy energia-impulzus vektora egyre kisebb m értéku hiperbolára illeszkedik), de már nagy sebességgel rendelkezik. Az ábráról le is olvasható ez a pillanatnyi sebesség:

Kérdés: Mi a 2. ábrára felvázolt szaggatott görbe V = tanα. (1) egyenlete? Azaz: milyen görbét ír le a gyorsítási folyamat közben a (csökkenő tömegű, növekvő sebességű) rakéta energia-impulzus vektorának csúcsa az E-p diagramon?
A fizikai elvek, amelyeket a kérdés megválaszolásához felhasználunk, a következők:
A 2. pontban leírtak szerint az éppen kilövellt kis hajtógázadag u = tanβ sebességét a relativisztikus sebesség-transzformációs képlet adja meg:
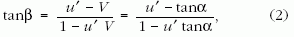
ahol u' (= konstans) a hajtógáz rakétához képest mért - másképpen: a rakétával éppen együttmozgó inerciarendszerben mért - sebessége.
(Az egyszerűbb geometriai áttekinthetőség kedvéért mind α-t, mind β-t pozitív számértékűnek választottam. Ennek megfelelően u'-t is pozitív számnak vettem. E választásnak csak annyi következménye lesz, hogy az alább szereplő (4) differenciálegyenletben megjelenik egy negatív előjel.)
A 2. ábra szaggatott görbéjére teljesül, hogy

valamint

A (3) és (4) összefüggéseket (2)-be behelyettesítve explicit alakban megkapjuk a keresett E(p) görbe differenciálegyenletét
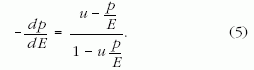
A görbe analitikus alakja az (5) differenciálegyenlet E(p =0) = mk kezdőfeltétel melletti megoldásával lenne megkapható, azonban, sajnos az (5) differenciálegyenletnek nincs analitikus megoldása.
Próbálkozzunk másképp: térjünk át (R,α) polárkoordinátákra, a 2. ábra jelölései szerint:

(A polárkoordinátákra való áttérés azért is kézenfekvő gondolat, mert a végsebesség csak az α szögtől függ.)
Két megjegyzés:
A (6) koordináta-transzformáció segítségével könnyen megkapható az (5) differenciálegyenlet polárkoordinátás alakja:
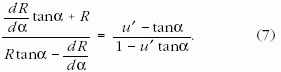
Ez egyszerű átalakítással az
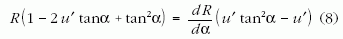
alakra hozható. A (8) differenciálegyenlet (a kezdőfeltételeket az integrálási határokba foglalva) közvetlen integrálással megoldható:
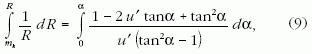
amelyből az
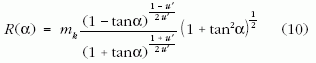
analitikus megoldást kapjuk.
A (10) egyenlettel felírt görbéket nevezhetjük "rakétagörbéknek": egy mk kezdeti tömegű rakéta energia- impulzus vektora a gyorsítási szakasz során egy-egy ilyen görbén fut végig az E-p diagramon. (Hogy melyiken, az az u? hajtógázsebességtől függ.) A 3. ábrán három ilyen rakétagörbét tüntettem fel, amelyek háromféle hajtógázsebességnek felelnek meg (u' = 0,1, 0,5, illetve 0,9).
A rakéta pillanatnyi energia-impulzus vektorát úgy kapjuk, hogy az origót összekötjük a rakétagörbe megfelelő pontjával (a 3. ábra illusztrálásképpen mutat egy ilyen energia-impulzus vektort, az u' = 0,5 esetre). A rakéta pillanatnyi sebessége ezután közvetlenül leolvasható, mint az energia-impulzus vektor (E-tengelyhez képesti) meredeksége.
Az ábrából látszik az az (intuíciónkkal is egyező) eredmény, hogy nagy rakétasebességek úgy érhetők el, ha a hajtógázsebességet nagyra választjuk, illetve ha a rakéta minél több hajtógázt bocsát ki. Az ábra azt is szemléletesen mutatja, hogy a rakéta sebessége minden körülmények között a fénysebességnél kisebb marad.
A rakéta mk kezdeti tömege a gyorsítási szakasz folyamán csökken, végső értéke mv. Mekkora az elért végsebesség? Nincs más dolgunk, mint meghatározni a rakétagörbe és az mv végső tömeghez tartozó hiperbola metszéspontját [1]: ez a pont adja meg a rakéta energia-impulzus vektorát a gyorsítási szakasz végén. A 4. ábra illusztrálja a geometriai eljárást (mv /mk = 0,7 és u' = 0,5 mellett).
Most nézzük a számolást! Az mv-hez tartozó hiperbola egyenlete:

A hiperbola egyenletét azonban szintén polárkoordinátás alakban keressük. Felhasználva a (6) koordinátatranszformációs képleteket, valamint a
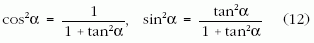
trigonometrikus azonosságokat, a hiperbola polár-koordinátás egyenletére
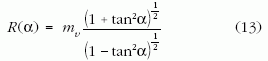
adódik. Mivel tanα éppen a rakéta V pillanatnyi sebessége, mind a rakétagörbe (10) egyenlete, mind a hiperbola (13) egyenlete közvetlenül átírható a rakétasebesség függvényére:
mk-ból induló rakétagörbe:
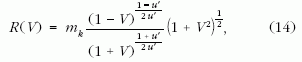
mv -hez tartozó hiperbola:
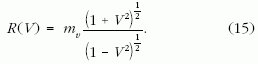
(14) és (15) jobb oldalát egyenlővé téve a következő kifejezés adódik a két görbe metszéspontjára:
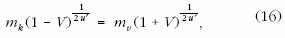
amiből a rakéta V végsebességére a jól ismert
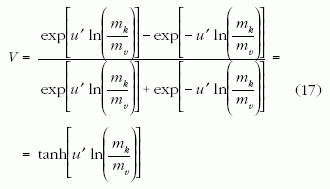
képletet kapunk.
A tangens-hiperbolikusz függvény a ±∞-ben ±1-hez tart, az ilyen (1-hez közelire választott u' és nagyra választott mk /mv tömegarány mellett megközelíthető) esetet nevezhetjük ultrarelativisztikusnak.
A jól ismert nemrelativisztikus formulát akkor kapjuk vissza, ha a tangens-hiperbolikusz argumentumában szereplő kifejezés kicsi: ilyenkor a tangens-hiperbolikusz függvény magával az argumentummal közelíthető, ezért
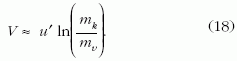
klasszikus kifejezést kapjuk.
_____________________
Köszönetemet fejezem ki Hraskó Péternek hasznos javaslataiért.