Fizikai Szemle honlap |
Tartalomjegyzék |
Fábián Margit
MTA SZFKI
A kérdés, hogy mi legyen a világszerte folyamatosan felhalmozódó radioaktívhulladék-készletekkel, óriási gondot jelent. Mostanra általánosan elfogadott műszaki megoldás az, hogy az atomhulladékot mélyen fekvő geológiai tárolóhelyeken eltemetik, vagyis elszigetelik a környezettől. Munkánk során radioaktív hulladékok tárolására alkalmas üvegösszetételt kerestünk, amely stabil, hosszú idejű tárolást tud biztosítani. Azt találtuk, hogy a több-komponensű boroszilikát üvegek alkalmasak a radioaktív magok stabil befogadására, így potenciális tárolóanyaggá válhatnak [1]. Előállításuk gazdaságos, fokozott óvatosság mellett nem igényel különleges előállítási feltételeket, nem oldódik savas, illetve lúgos kőzegben, jó termikus tulajdonságokkal rendelkezik.
Ahhoz, hogy egy több-komponensű üvegrendszerbe az UO3 beépülését meg tudjuk határozni, ismernünk kell az egyszerűbb minták lehetséges szerkezetét. Ezért mintasorozatainkat szisztematikusan, egy-egy új komponenssel kibővítve állítottuk elő. A két komponensű, egyszerű összetételekből kiindulva vizsgáltuk a három-, öt- és hatkomponensű üvegek szerkezetét. Elsőként a B2O3 és SiO2 alapoxidok szerkezetét modelleztük a fordított Monte Carlo (RMC) szimulációs módszerrel [2], hogy saját eredményekre tudjunk támaszkodni a bonyolultabb összetételek tanulmányozásakor. Még több és pontosabb információval gazdagodtunk a 70SiO2 · 30Na2O és (75-x)SiO2 · xB2O3 · 25Na2O (x = 5-15 mol%) minták szerkezeti vizsgálata során. Mintáinknál ugyanazokat az előállítási feltételeket alkalmaztuk, ugyanazokat a mérési eljárásokat használtuk és hasonló módon történt a kiértékelés is, ami nagyban hozzájárult ahhoz, hogy megfelelően tudjuk öszszehasonlítani az eredményeket, illetve értelmezni a kapott lehetséges szerkezeteket.
Legfőbb célunk a különböző radioaktív hulladékok tárolására megfelelő üvegmátrixot találni. Meghatározni a maximálisan adalékolható UO3 mennyiséget, vizsgálni az urán beépülését és az urán környezetét, valamint hatását az üveg stabilitására és a higroszkopikus tulajdonságaira.
Az atomi szerkezet meghatározására neutron- és röntgendiffrakciós méréseket végeztünk, az adatok kiértékelésére a fordított Monte Carlo szimulációs módszert használtuk [2], amely az amorf rendszerek leírására széles körben alkalmazott eljárás. Azonban egy ilyen, sok különböző atomot tartalmazó rendszer nem megszokott az RMC modellezésnél. Ezek vizsgálata kihívást jelent, az eddigi tanulmányokat tekintve nincs jól bevált séma.
Az üvegmintákat olvasztással állítottam elő, kiinduló anyagként minden esetben por oxid-keveréket használtam. Kiindulási anyagaink a SiO2, B2O3, Na2CO3, BaO, ZrO2 és UO3 voltak. A természetes bór nagy neutronabszorpciója miatt B-11 izotópban dúsított (99,6%) diborátot alkalmaztunk (Sigma-Aldrich Co.).
Az olvasztásra magas hőmérsékletű (1600 °C-ig fűthető) KOII típusú elektromos felfűtésű kályhát használtam, 1350-1450 °C hőmérséklet-tartományban. Az olvasztást platinatégelyben végeztem, az olvadék homogenitását cseppellenőrzéssel figyeltem. Természetes uránt használtunk, ami radioaktív. Mintáink aktivitása ugyan kicsi, körülbelül 2,7 kBq/g, de fokozott figyelmet igényeltek.
Jelen cikkben a mátrixüveg és az U-tartalmú mintasorozatokra kapott eredményeket mutatom be: a (65-x)SiO2 · xB2O3 · 25Na2O · 5BaO · 5ZrO2 (SiB(5-10-15)NaBaZrO rövidítést, illetve B5, B10, B15 jelölést) és a 70s%[(65-x)SiO2xB2O325Na2O5BaO5ZrO2]+30s%UO3 (SiB(5-10-15)NaBaZrUO rövidítést, illetve a UB5, UB10, UB15 jelölést alkalmazom a továbbiakban), ahol mindkét esetben x = 5, 10, 15 mol%. A diffrakciós méréseket minden esetben por mintán végeztem, ehhez a tömbi amorf mintát achátmozsárban porítottam.
A vizsgált több-komponensű mintáink könnyű és nehéz atomokat egyaránt tartalmaznak, ezért indokoltak voltak a neutron- és röntgendiffrakciós mérések. A könnyű atomok környezetére (B, O, Si) a neutrondiffrakció ad pontosabb szerkezeti információt, míg a nehéz atomokra (Ba, Zr, U) a röntgendiffrakciós mérésből nyerhetünk több információt. A neutrondiffrakciós méréseket a Budapesti 10 MW Kutatóreaktornál működő PSD elnevezésű [3] neutron-diffraktométeren végeztem. A mintán szóródó monokromatikus neutronnyaláb hullámhossza λ0 = 1,068 Å volt. A teljes szórási spektrumot Q = 0,45-9,8 Å-1 tartományban mértem, ahol Q = 4πsinΘλ, Θ a Bragg-szög, λ a hullámhossz. Mintáink egy részét megmértem a Los Alamos-i impulzus-neutronforrásnál működő NPDF berendezésen is [4]. A repülési idő technikánál a hullámhosszat változtatjuk a detektorok állandó szöghelyzete mellett. Ezek a mérések lehetővé teszik a mérési tartomány kiterjesztését nagy Q-tartományig, jellemzően 30-50 Å-1-ig. Ennek előnye, hogy a valós r-térben a g(r) atomi párkorrelációs függvények számításánál jó felbontást kapunk (Δr = 2π/Qmax)1. A budapesti PSD és a Los Alamos-i NPDF mérések adatainak összeillesztésével kiszámoltuk az S (Q) szerkezeti függvényt.2
A röntgendiffrakciós méréseket a hamburgi Desy-szinkrotronnál működő BW5 röntgen-diffraktométeren végeztem [5], ahol a monokromatikus hullámhossz λ0 = 0,113 Å volt, 109,5 keV energián. Valamennyi mintát a Q = 0,5-25 Å-1 szórási tartományban mértük. Az adatok feldolgozásánál figyelembe vettük a háttér- és abszorpciós korrekciókat. A két fajta diffrakciós mérés együttes kiértékelését az RMC szimulációs programba történő beépítéssel végeztük.
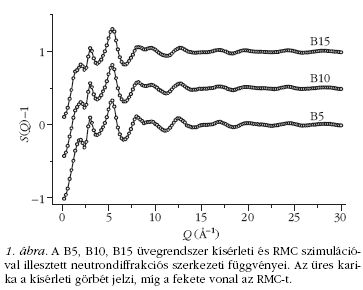
Több-komponensű minták esetén az egyes atompárokat jellemző gij (r) parciális szerkezeti függvények3 meghatározásához a fordított Monte Carlo (RMC) módszert használjuk, amely rendezetlen kondenzált rendszerek diffrakciós spektrumainak értelmezésére széles körben alkalmazott eljárás [2, 6]. Az RMC szimuláció során részecskéket mozgatunk egy szimulációs cellában, véletlenszerűen és időtől függetlenül úgy, hogy a rendszer jellemzőiből számolt szerkezeti függvény a kísérleti diffrakciós adatokkal a lehető legjobban egyezzen. A dobozban lévő részecskék háromdimenziós koordinátarendszerben való elhelyezkedéseinek összességét tekintjük a részecskekonfigurációnak. Szimulációs dobozunk minden esetben 5000 atomot tartalmazott. A szimulációs program felépítéséhez felhasználtuk a korábban lefuttatott egyszerűbb összetételű minták eredményeit [7-9]. A jó illeszkedés eléréséért kényszereket alkalmaztunk, az atomi távolságok megkötése mellett koordinációs kényszereket, ezen adatok ismerete előző munkáink eredménye [8,9]. Az 1. ábra az RMC modellezéssel illesztett neutrondiffrakciós szerkezeti függvényeket mutatja be a B5, B10, B15 mátrixüvegekre.
Az RMC program által generált szerkezeti függvények mindhárom minta esetén jó egyezést mutatnak a kísérleti spektrumokkal, ugyanakkor azt is megfigyelhetjük, hogy a minták szerkezeti függvényei hasonló jellegűek. Az RMC szimulációs módszerrel meghatároztuk az atompárok parciális eloszlásfüggvényeit és a koordinációs számeloszlásokat.4 Az alapszerkezetet felépítő Si és B üvegalkotó atomok környezetére vonatkozóan a 2. ábra a Si-O és B-O atomi parciális párkorrelációs eloszlásfüggvényeket és a koordinációs számeloszlást mutatja be.
Az rSi-O = 1,60±0,01 Å távolságra, valamint a koordinációs számokra kapott 3,9; 3,7; 3,9 értékek a SiO4 tetraéderes kialakulásának valószínűségét mutatják, amit alátámaszt a Si-Si stabilan kialakuló 3,0 Å távolsága is. Ezek az értékek az előzőleg vizsgált amorf SiO2 és 70SiO2 · 30Na2O munkáink eredményével teljes összhangban vannak [8]. A B-O elsőszomszéd-távolságra kapott két érték közül az egyik, az eddig ismert 1,40±0,01 Å távolságnak felel meg, a második 1,60±0,01 Å távolság pedig új eredményként jelenik meg, amelyre irodalmi utalást nem találtunk. A B-atom 3,5; 3,1; 3,15 koordinációs számait meghatározva és eloszlásukat figyelembe véve azt mondhatjuk, hogy trigonális BO3 ([3]B) és tetraéderes BO4 ([4]B) egységek kialakulásaira van lehetőség. A második rB-O = 1,60 Å csúcs értéke pontosan megegyezik az rSi-O = 1,60 Å távolsággal, ez alapján azt mondhatjuk, hogy négyes koordináltságú BO4 és SiO4 szerkezeti egységek kapcsolódnak össze. Az első 1,40 Å csúcsot feltehetően a [3]B koordinációjú B egységek, míg a második 1,60 Å csúcsot vegyesen [3]B és [4]B egységek alkotják. Ebből arra következtetünk, hogy a szerkezet felépítésében kevert állapot jelenik meg, ahol a szerkezetépítő egységek a [3]B-O-[4]Si és [4]B-O-[4]Si vegyes láncot alkotják. A szerkezeti egységek egymáshoz való kapcsolódása látható a 3. ábrán, mindezt - az ábrázoló program korlátai miatt - 500 atomra vonatkoztatva. A SiO4 tetraéderes egységek kialakulása mellett megfigyelhető a trigonális BO3-ra és a tetraéderes BO4-re jellemző egységek kialakulása, az így kialakuló üregek biztosítják a nagy radioaktív magok stabil beépülését.
A fent bemutatott mátrixüveg szerkezete az uránoxiddal bővül. Fontos megjegyezni, hogy az uránt tartalmazó mintasorozatunk közül egy mintánk sem volt higroszkópos, mint ahogy a mátrixsorozatunk mintái sem. Jóllehet, az előállításukat követően exikátorban tároljuk, de több hónapnyi (most már évnyi) idő elteltével sem mutattak higroszkópos jelleget. Mintáinkat félévente neutrondiffrakciós méréssel ellenőriz- zük, minden eddigi esetben amorf jellegű spektrumot kaptunk; nem kristályosodnak át, ez stabil szerkezetre utal. Az urános sorozat mintáit a PSD neutron-diffraktométeren (λ0 = 1,068 Å) és a BW5 röntgen-diffraktométeren (λ0 = 0,113 Å) mértem meg. Az urán radioaktivitása miatt adminisztrációs akadályokba ütköztünk, ezért ezt a sorozatot nem sikerült kiterjesztett Q-tartományon, az NPDF berendezésen megmérni. Az adatok feldolgozására ez esetben is az RMC szimulációs programot használtam.
A 4. ábrán a neutron- és röntgendiffrakciós szerkezeti függvények illesztését mutatom be az UB5, UB10, UB15 sorozatra.
Ha ezeket a neutrondiffrakciós szerkezeti függvényeket összevetjük a korábban tanulmányozott mátrixsorozat szerkezeti függvényeivel az azonos Q-tartományon, hasonlóság figyelhető meg a két sorozat között. Ez arra utal, hogy az UO3 bevitelével az üvegszerkezet lényeges elemei nem változnak.
Az RMC programot a mátrixsorozatnál kapott eredmények segítségével építettem fel, a mindkét mintasorozatnál jelenlevő parciális párkorrelációs függvények hasonló karakterisztikát adnak és hibán belül azonos értéknél alakítják ki a csúcsokat. A Si-O (1,60±0,01 Å) és a B-O (1,35/1,55±0,1 Å) elsőszomszéd- távolságok nagyon jó egyezést mutatnak a mátrixüvegnél kapott eredményekkel, ami azt bizonyítja, hogy a megismert alapszerkezet nem változik az UO3 bevitelével. Az 5. ábra a parciális párkorrelációs függvényeket mutatja be a három mintára. Mindhárom minta esetén az U-O parciális függvényre nagyon élesen felhasadó két csúcsot kapunk; egy kisebb távolságnál kialakuló nagyobb intenzitású maximum 1,8; 1,84; 1,75±0,1 Å értékeknél, míg a második csúcs magasabb értéknél kisebb intenzitással alakul ki, de mindhárom minta esetén hibán belül azonos távolságnál, 2,24; 2,24; 2,2±0,1 Å, az UB5, UB10, UB15 sorrendnek megfelelően. Irodalmi adatok alapján kristályos anyagokban uranil ion [UO2]2+ formálódik U-Oaxiális 1,8 Å távolsággal, ami jó egyezést mutat eredményünkkel. A második csúcs igen stabil és szimmetrikus, ami megfeleltethető az uranil ion U-Oekvatoriális távolságának, jellegzetesen 2,2-2,24 Aring; értékeknél. Az RMC-vel számolt átlagos koordinációs számokra: K.Sz.Si-O = 3,95; 3,90; 3,64; a K.Sz.B-O = 3,47; 3,45; 3,1 értékeket kapunk, ami igen jól egyezik a mátrixüvegnél kapott Si-, B-atomok koordináltságával. Ezen értékekből azt a következtetést vonjuk le, hogy az urántartalmú üvegek alapszerkezetét is [3]B és [4]B koordinációjú B-atomok vegyes trigonális és tetraéderes [3]B-O-Si és [4]B-O-Si környezetek alkotják (6.a ábra).
Az uránatom környezetére a koordinációs számokból következtethetünk. A K.Sz.U-O = 5,39; 5,55; 4,93 értékeket kaptuk. Irodalmi adatok alapján azt tudjuk, hogy az U(VI), U(V) és U(IV) koordináltsággal vesz részt vegyületeiben, a kapott eredményeink egyezőek az irodalmi adatokkal (6.b ábra). Azt mondhatjuk, hogy a rövidebb 1,84 Å távolságnál az U-atom kettő O-atomot koordinál axiális pozícióban, a magasabb értéknél kialakuló 2,24 Å távolságban három, többségben négy oxigénatomot von magához az ekvatoriális pozíció kialakításáért.
Mindhárom minta esetén erős korreláció figyelhető meg az U-atom és a Si, B üvegalkotó, a Na módosító és a Zr stabilizáló atomok között meglepően alacsony értékeknél, jellegzetesen 2,85-3,7 Å távolságoknál. A 7. ábrán a másodszomszéd-távolságoknál formálódó U-Si, U-B, U-Na és az U-Zr parciális atomi párkorrelációs függvényeket láthatjuk.
Sikerült előállítani olyan több-komponensű mátrixüveget, amely alkalmas lehet a radioaktív magok stabil befogadására. Meghatároztuk az 5-komponensű mátrixüveg szerkezetét jellemző legfontosabb atomi elsőszomszéd-távolságokat és a koordinációs-számeloszlásokat. Megállapítottuk, hogy a mátrixüveg szerkezeti felépítésében elsősorban a tetraéderes koordináltságú (SiO4)4- egységek játszanak fontos szerepet, míg a bór 3-as és 4-es koordináltságú oxigénkörnyezetekben helyezkedik el. A bór egy része beépül a Si-alapú hálószerkezetbe és [3]B-O-[4]Si, illetve [4]B-O-[4]Si vegyes láncok alakulnak ki. Előállítottuk és vizsgáltuk a 6-komponensű urántartalmú üvegsorozatot, amely az eddig ismert legnagyobb mennyiségben képes UO3-t befogadni. A neutron- és röntgendiffrakciós mérések kiértékelése során azt kapjuk, hogy nagyon stabil, amorf rendszer jön létre. Az urántartalmú minták alapszerkezetének felépítését tetraéderes SiO4 egységek és vegyes trigonális BO3 és tetraéderes BO4 egységek teszik lehetővé; a vegyes láncszerű váz kialakulása biztosítja az U-atom beépülését.
Az üveg alapszerkezete nem változik az U-atom bevitelével. Az U-O atomi parciális korrelációs függvény két elsőszomszéd-távolságnál mutat éles eloszlást. A karakterisztikus másodszomszéd-távolságok kialakulása nagyfokú szerkezeti stabilitásra utalnak, ahol az U-atom O-atomon keresztül kapcsolódik közvetlenül az üvegképző, módosító és stabilizáló Si-, B-, Na-, Zr-atomokhoz. Az U-atom átlagosan 5,6 O-atomot koordinál. Ezek az eredmények arra engednek következtetni, hogy az U az alapszerkezetbe épül be és vesz részt a szerkezetfelépítésben, így stabilizálva a rendszert. Vizsgálataink alapján feltételezhető, hogy a boroszilikát üvegek a bemutatott összetétellel radioaktív hulladékok potenciális tárolóanyagaként használhatók, jelentős gazdasági és környezeti megoldásokat kínálva a nagy aktivitású radioaktív hulladékok biztonságos tárolására.
________________________
1 Nemkristályos, azaz amorf (üveg) állapotú anyagok szerkezetének
jellemzésére a g(r) atomi párkorrelációs függvényt használjuk,
ami megadja annak valószínűségét, hogy az r = 0 helyen lévő atomtól
r távolságban lévő másik atom milyen valószínűséggel fordul
elő. Mivel izotróp rendszerekről van szó, r skaláris mennyiség. Az
alkalmazott formalizmust részletesen leírtuk több cikkünkben [9].
2 Az S(Q) szerkezeti függvény a szórt intenzitáseloszlásból számolt
koherens, rugalmas szórás normált alakja, figyelembe véve a
háttér, abszorpció és az adott mérőberendezésre jellemző egyéb
korrekciós tényezőket.
3 A gij (r) parciális párkorrelációs függvény megmutatja, hogy egy
i típusú részecskétől r távolságban a j típusú részecskék lokális sűrűsége
hogyan aránylik az j típusú részecskék átlagos sűrűségéhez.
4 A K.Sz.ij koordinációs szám megadja, hogy egy i típusú atomot
átlagosan hány j típusú atom vesz körül egy megadott távolságtartományban.