VEKTOROK PÁRHUZAMOS ELTOLÁSÁNAK SZEMLÉLTETÉSE - II. RÉSZ
A Foucault-inga és egyebek

Bokor Nándor, BME Fizika Tanszék
Laczik Bálint, BME Gyártástudomány és -technológia Tanszék

Cikkünk első részében először általánosságban vizsgáltuk a vektorok párhuzamos eltolásának kérdését. Ezután egy érdekes antik eszköz, a kínai délirányt jelző működését mutattuk be, amely a jelenséget fizikailag is illusztrálja: miközben a kordé adott felületen adott görbe mentén gurul, a ráerősített jelző kar "tartja az irányát", pontosabban: párhuzamosan tolódik el. Cikkünk második részében néhány további illusztrációt mutatunk be arra, hogy a párhuzamos eltolás jelensége hol érhető tetten a természetben.

A Foucalt-inga

A Léon Foucalt által javasolt, és először a 19. század közepén elvégzett ingakísérlet a fizika leghíresebb vizsgálatai közé tartozik. A hosszú fonálra felfüggesztett pontszerű tömeg lengési síkja elfordul a Földhöz rögzített vonatkoztatási rendszerhez képest, szemléltetve ezzel a Föld forgását.¹ Manapság is előfordul, különösen a fizikát népszerűsítő irodalomban, az a megfogalmazás, hogy a jelenség oka: a matematikai inga a Föld mozgásától függetlenül megőrzi lengési síkját a globális inerciarendszerhez, azaz az állócsillagokhoz rögzített vonatkoztatási rendszerhez képest. Ezen állítás képtelenségét egyszerű gondolatkísérlettel beláthatjuk: képzeljünk el egy ingát, amelyet az Egyenlítőnél függesztenek fel, és éjfélkor észak-dél irányban hoznak lengésbe. Ha az inga valóban megőrizné lengési síkját az állócsillagokhoz képest, akkor reggel 6-kor a kísérletet végzők feje felett, vízszintes (!) síkban kellene lengenie, ami nyilvánvalóan képtelenség. Valójában csak két olyan földrajzi hely van, ahol - a kezdeti kitérítés irányától függetlenül - az inga megőrzi lengési síkját az állócsillagokhoz képest: az Északi- és a Déli-sark.

Nem segít a helyzeten, hogy időnként még az olyan nagyszerű és precíz tankönyvek is félreérthetően fogalmaznak, mint Budó Ágoston Mechanikája: "a Föld nem lehet inerciarendszer, de (…) ilyennek tekinthető egy olyan rendszer, amelynek például a z -tengelye a Föld forgástengelye, az xy-síkot pedig a Föld középpontja és bizonyos állócsillagok határozzák meg; ebben a rendszerben ugyanis az inga lengési síkja nem fordul el" [1]. A zavarhoz - önhibáján kívül - valószínűleg maga Foucault is hozzájárult, hiszen nevezetes cikkében [2] szerepel az a félmondat, hogy "a lengési sík nem fordul el, hanem rögzített marad a térben", ha azonban figyelmesen olvassuk el a bekezdést, rögtön kiderül, hogy itt egy olyan laboratóriumi kísérletről beszél, amikor egy forgó dobra helyezett fémrúd rezgését vizsgáljuk, és a fémrúd nyugalmi helyzete egybeesik a dob forgástengelyével. Ekkor - és analóg módon akkor, amikor a Foucault-inga az Északi- vagy a Déli-sarkon leng - valóban igaz a lengési (rezgési) sík állandósága a térben. Más szélességi körökön azonban nem, hiszen az ingára teljesülnie kell azon kényszerfeltételnek, hogy a lengési sík átmenjen a Föld középpontján.²

Az adott szélességi körön felállított Foucault-inga egy nap alatti szögelfordulását az alábbiakban a www.sciencebits.com/foucault honlapon található levezetés alapján tárgyaljuk.

Vizsgáljuk a fonál végére függesztett m tömegű tömegpont mozgását a Föld érintősíkjában (a tömegpont jó közelítéssel ebben a síkban mozog), a Földhöz rögzített vonatkoztatási rendszerben, (r, θ, z) hengerkoordinátákat használva. Az r koordináta a tömegpont távolsága az egyensúlyi helyzettől, θ, ?a lengés szöghelyzete valamilyen kitüntetett irányhoz (például az északi irányhoz) képest, z pedig a függőleges (azaz a Föld középpontjától elfelé mutató) irány (1. ábra). A tömegpontra a nehézségi erő, a fonál húzóereje és a Coriolis-erő hat (a centrifugális erőt elhanyagoljuk).

A nehézségi erő és a fonálerő összetehető egy olyan rugalmas visszatérítő erővé, amely a Hooke-törvénynek engedelmeskedve a kitéréssel egyenesen arányos - ez lesz felelős a lengőmozgásért -, míg a Coriolis-erő a lengési sík oldalirányú elfordulását okozza. Newton 2. törvénye szerint:

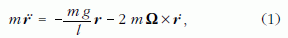
ahol r a tömegpont helyvektora, Ω pedig a Föld forgási szögsebessége. Könnyű belátni, hogy a fenti mozgásegyenletben szereplő vektorok komponensei az (r, θ, z) hengerkoordináta-rendszerben, a Föld adott λ szélességi körén:

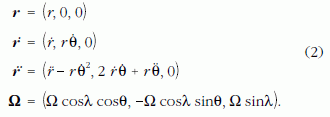
Az előbbi komponensalakokat felhasználva és az (1)-ben szereplő vektori szorzatot kibontva a mozgásegyenlet θ,-komponensére a következő egyenletet kapjuk:

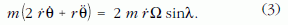
A Foucault-ingára érvényes az adiabatikus közelítés (amely egyébként valamilyen formában rendszeresen felbukkan az ilyen típusú, úgynevezett geometriai fázissal kapcsolatos jelenségeknél): Az inga ω lengési körfrekvenciája (amely tipikusan ~rad/s nagyságrendű) sokkal nagyobb, mint az a körfrekvencia, amellyel az inga felfüggesztési pontja körbehalad (ez ugyanis a Föld szögsebességével egyezik meg, azaz 2π rad/nap). Ráadásul a lengési sík körbefordulásának körfrekvenciája is, mint kísérleti tapasztalatból tudjuk, ~2π rad/nap nagyságrendjébe esik.³

Ekkor - az inga lengésének, illetve a lengési sík elfordulásának sok nagyságrenddel eltérő periódusát figyelembe véve - a következő nagyságrendi becslések végezhetők:

illetve

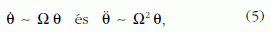
így a (3) egyenlet bal oldalán szereplő két tag arányára a következő adódik:

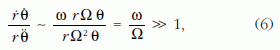
vagyis a (3) egyenletben az r θ tag elhanyagolható. A kapott közelítő egyenletből közvetlenül adódik az inga lengési síkjának elfordulási szögsebessége:

Mekkora T idő alatt fordul el a lengési sík - a Földhöz rögzített vonatkoztatási rendszerben! - éppen annyit, hogy az inga visszatérni látszik eredeti orientációjához? Ez éppen a π elfordulási szöghöz tartozó időtartam, amely (7) alapján számolható:

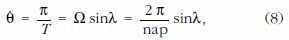
tehát

Ellenőrzés: a (9) képletből a Déli- és Északi-sarkra T = 12 óra adódik, az Egyenlítőre pedig T = ∞ (nem fordul el a lengési sík), amint azt várjuk is.

Mint már megjegyeztük, a Foucault-féle ingakísérlet eredeti célja a Föld tengelyforgásának demonstrálása volt. Egyszerű aránypár felállításával könnyű kiszámítani, hogy egy nap alatt mekkora αszöggel fordul el a lengési sík a Földhöz rögzített vonatkoztatási rendszerben:

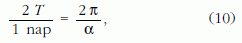
azaz (9) felhasználásával:

Ez az eredeti kísérlet helyszínén, Párizsban naponta mintegy 271°-os elfordulást eredményezett.

Több, mint gyanús, hogy a (11) eredmény tökéletesen megegyezik azzal a - Gauss-Bonnet-tételből számolható - szögelfordulással, amely egy gömb adott λ szélességi körén párhuzamosan körbevitt vektorra adódik egy teljes kör megtétele után. Valóban, mint mechanikai megfontolásokból közvetlenül is megmutatható, a Foucault-inga lengési vonala párhuzamos eltolást szenved a Föld felületén az adott szélességi kör mentén. Annak természetesen nincs jelentősége, hogy ebben az esetben a vektort képviselő objektumot fizikailag nem mi hordozzuk körbe egy álló gömb felületén - mint a kordé esetében tettük, a Földet ugyanis annál a kísérletnél álló gömbnek tekinthettük -, hanem a Föld napi forgása teszi meg nekünk ezt a szívességet.

Mivel a Foucault-ingát nem a Gauss-Bonnet-tétel kvantitatív igazolására találták ki, így nem is kérhető számon rajta, hogy erre a célra kevésbé rugalmasan használható, mint a délirányt jelző kordé. Összefoglalhatjuk, melyek a Foucault-inga hátrányai a kordéval szemben (ha a Gauss-Bonnet-tétel demonstrálására akarjuk használni mindkettőt):

• A Foucault-inga csak egy bizonyos típusú felületen (nevezetesen a Földön, mint gömbfelületen), és annak is csak nevezetes vonalai (a szélességi körök) mentén végzi a párhuzamos eltolást.
• Egy-egy kísérletező kényelmesen csak egyetlen görbén végezhet mérést (azon a szélességi körön, amelyen tartózkodik), új kísérletekhez nagy távolságokat kell utaznia.
• A Gauss-Bonnet-tétel demonstrálásához (azaz az inga zárt görbén való végigviteléhez) szükséges kísérlet egy teljes napot igénybe vesz.
• Meg kell oldani, hogy az inga lengése a kísérlet 24 órája alatt ne csillapodjon számottevően.
  Van viszont az ingának egy nagyon vonzó tulajdonsága: felépítésének végletes egyszerűsége (hasonlítsuk ezt össze a kordé bonyolult fogaskerék-rendszerével!). A fenti hátrányok közül is kiküszöbölhető néhány, mint azt az alább felsorolt szellemes javaslatok mutatják.
• A Foucault-inga csillapításmentes változata elkészíthető olyan módon, hogy a függőleges fonál végére rögzített vasgolyót egy alkalmasan beállított elektromágnes kényszeríti ingamozgásra [3]. Az ilyen állandó üzemű inga esetében nem szükséges a lengésidőt - és ezzel együtt a méretet - nagyra választani, így kompakt, hordozható Foucault-inga készíthető, amellyel folyamatos üzemmódban, akár hónapokon keresztül végezhetők a mérések.
• A Foucault-inga működésének demonstrálására kicsinyített makett is készíthető. Itt nem a Föld forgásának a bemutatása a cél, hanem annak igazolása, hogy egy forgó asztalra (ez modellezi a forgó Földet) helyezett inga lengési síkja valóban a Gauss-Bonnet-tétel szerinti mértékben fordul el. E kísérlet egyik lehetséges változata az, amikor az "ingát" nem fonál végéhez rögzített tömegpont, hanem merev rúd alkotja [4]. A gravitáció által előidézett lengőmozgás szerepét a megpendített merev rúd rugalmas rezgése veszi át. Az elrendezés nagy előnye, hogy a forgó asztalra szerelt, felső végén befogott merev rúd tetszőleges mértékben megdönthető a függőlegeshez képest, ilyen módon tetszőleges szélességi kör mentén lezajló lengőmozgás kvantitatíven modellezhető. A merev rúd szabad vége ugyanis (jó közelítéssel, ha a gravitáció által okozott meghajlástól eltekintünk) a rögzített ferde pozícióhoz képest végez rezgőmozgásokat. További előny, hogy az adiabatikus feltétel már sokkal kisebb időskálán is teljesül: a rúd rezgésének frekvenciáját 10 Hz körüli értékre állítva [4] az asztal teljes körbefordulásának idejét akár néhány másodpercnyi rövidségűre is választhatjuk. Így az egynapos normál Foucault-kísérlet néhány másodperc alatt "kicsiben" lejátszható. A megpendített rúd gyors rezgése elmosódott síknak látszik, amelynek lassú elfordulása könnyen megfigyelhető. Történeti érdekesség [2, 4], hogy e kísérleti elrendezés gondolata közvetlenül Foucault-ig nyúlik vissza: mielőtt ugyanis híres gravitációs ingakísérletét elvégezte, először egy egyik végén esztergapadba befogott merev rúd rezgésének vizsgálatával győződött meg arról, hogyan fordul el a rezgési/lengési sík egy forgó rendszerhez képest!

Parallelométer

A délirányt jelző kordén és a Foucault-ingán kívül más mechanikai eszközök is léteznek, amelyek párhuzamos eltolást valósítanak meg. Az egyik legegyszerűbb a nevében is erre a funkcióra utaló a parallelométer [5], amely nem más, mint egy talapzatra szerelt súrlódásmentes lendkerék (2. ábra).

Egy adott görbült felület vizsgálatakor gondoskodnunk kell róla, hogy a lendkerék mindenhol csak a felület érintősíkjában foroghasson el. Ezt a kényszerfeltételt úgy lehet egyszerűen kielégíteni, hogy a parallelométer talapzatát az adott felületen csúsztatva mozgatjuk (tehát nem emeljük el a felülettől), ügyelve arra, hogy a talapzathoz merőlegesen erősített forgástengely, amelyen a lendkerék elforoghat, mindvégig merőleges maradjon a felületre.⁴ A lendkereket nem hozzuk forgásba. Mivel a kiegyensúlyozott lendkerékre az eszköz eltolása közben nem hat forgatónyomaték, küllői párhuzamos eltolást szenvednek az adott felület adott görbéje mentén.

Összefoglaló megjegyzések és egyéb fizikai analógiák

A Gauss-görbület fogalma nagyszerűen bevált felületek görbültségének leírására. Szépsége, hogy a felület adott pontjában egyetlen számadattal képes kvantitatíven jellemezni a görbültség mértékét és jellegét (negatív, illetve pozitív). Hiányossága, hogy definiálásához külső nézőpont szükséges - elvégre a felületben élő laposlények világából nézve nem léteznek, csupán matematikai absztrakciók azok a merőleges síkok, amelyek a cikkünk előző részében felírt (6) egyenletben szereplő Rmin és Rmax értelmezéséhez szükségesek. Ezt a hiányosságot ellensúlyozza Gauss nevezetes tétele, a Theorema Egregium, amely kimondja, hogy a (6)-tal definiált K Gauss-görbület kiszámítása kizárólag belső mérések segítségével is elvégezhető. Más szóval, létezik K-ra egy olyan képlet, amelyben nem az R_min és R_max "elvont" fogalmai szerepelnek, hanem csupa olyan mennyiség, amelyek szemléletes jelentéssel, mérhető fizikai tartalommal bírnak a laposlények számára.⁵

Kettőnél nagyobb dimenziószámú sokaság (például háromdimenziós terünk) esetén azonban alapvetőbb nehézségekbe ütközünk. Mint kiderül, a görbület adott pontbeli jellemzésére ekkor már nem alkalmas egyetlen szám. Természetesen továbbra is kényelmetlen már a kiindulás is: ha a (6) definíció Gauss-féle filozófiáját akarnánk akár háromdimenziós terünkre általánosítani, négydimenziós nézőpontot kellene felvennünk, amire - "háromdimenziós laposlényekként" - alkatilag képtelenek vagyunk.

A megoldás kulcsát a zseniális matematikus, Riemann találta meg. Legfontosabb gondolata: a görbületet olyan mennyiséggel kell jellemezni, amelyet - ellentétben a (6) képlet "filozófiájával" - már eleve belső nézőpontból lehet definiálni. Felismerte, hogy egy adott sokaság görbülete valóban jellemezhető egy olyan (pontról pontra más-más értékeket felvehető) többkomponensű mennyiséggel, egy tenzorral, amelynek már a definíciós képletében csakis a sokaság mérhető belső adatai szerepelnek, nem kell közben magasabb dimenziójú nézőpontra váltanunk.⁶

Szemléletünk a magasabb dimenziójú sokaságok esetén így is óhatatlanul nehézségekbe ütközik. A párhuzamos eltolás fogalma például már háromdimenziós görbült tér esetén sem olyan szemléletes, mint görbült felületen volt.⁷

Görbült téridő

Elméletével Riemann nem csak a matematika új ágát indította el, hanem a fizika egyik nagy forradalmát is elősegítette: kiderült ugyanis, hogy a Riemann-geometria ideális matematikai keretet nyújt a gravitáció elméletének formába öntéséhez. Einstein általános relativitáselméletének lényege, hogy a négydimenziós téridő egy olyan görbült sokaság, amelynek (1) görbületét a tömegek (pontosabban az adott téridőtartományban levő energia és impulzus) okozzák, és amelyben (2) a szabad tömegpontok a görbült sokaság "egyenesei" (geodetikusai) mentén mozognak.

A fenti (1) pontot átfogalmazva: a téridő görbületét minden "téridőpontban" (azaz eseménynél) egy olyan Riemann-tenzor írja le, amelyet az adott téridőpontbeli energia és az impulzus határoz meg.⁸ A (2) pontnál egy kicsit hosszabban időzzünk. A kérdés ugyanis az: mit nevezünk egy négydimenziós görbült téridőben geodetikusnak?

Itt emlékeztetünk arra, hogy euklideszi síkon az egyenes definiálása kétféleképpen történhet:

• Az egyenes olyan vonal, amelynek érintővektora a vonal mentén párhuzamos eltolást szenved.
• Az egyenes olyan vonal, amely az adott két pontot összekötő vonalak között a legrövidebb.

Mindkét definíció egyszerűen átmenthető magasabb dimenziószámú, görbült terek esetére is. A görbült téridőre való általánosítás azonban nem triviális. Ráébredni, hogy a tér és az idő nem rendelkezik önálló, abszolút létezéssel, csupán egy egybefüggő rendszer különböző "irányú" vetületei, már önmagában forradalmi gondolat (amely Hermann Minkowski nevéhez fűződik, és eleinte maga Einstein is idegenkedett tőle); nem lepődhetnénk meg tehát, ha ez a fajta sokaság kicsit másképp viselkedne, mint egy olyan, ahol például az összes "irány" térszerű.

Kiderül, hogy - a fenti kétféle definíció analógiájaként - a görbült téridő geodetikusainak a definiálása is kétféleképpen történhet:

• A geodetikus olyan világvonal, amelynek a kiinduló "pontban" (a kiinduló eseménykor) meghúzva érintővektorát, és a világvonal mentén párhuzamosan eltoljuk, az végig a világvonal érintője marad9 [6].
• (Tömegpontokra) a geodetikus olyan világvonal, amelyhez az adott két eseményt összekötő világvonalak között a leghosszabb sajátidő tartozik. Más megfogalmazásban: ha adott pontból, adott időben több ikertestvért is útnak indítűnk, azután egy későbbi időpontban ismét összehozzuk őket, akkor a randevú pillanatáig az az ikertestvér öregszik a legtöbbet, aki a két esemény között geodetikuson (azaz erőmentes állapotban, "szabadon esve") mozgott. Ez az úgynevezett "maximális öregedés elve" [7].

Rövid kitérő: a relativitáselmélet egyik legnépszerűbb pedagógiai példázata az iker-paradoxon. Egyszerű megfogalmazásban: az űrállomáson maradt ikertestvér többet öregszik, mint az, aki oda-vissza utat tesz egy távoli bolygó és az űrállomás között. A fentiekből viszont következik, hogy az "oda-vissza" szóval óvatosan kell bánni. Az eredeti változatban az "egy helyben maradt" ikertestvér végig egy szabadon lebegő (és elhanyagolható tömegű!) űrállomáson tartózkodik, azaz sík téridőben, erőmentes, szabad mozgást végezve. A maximális öregedés elve egyértelmű: ő mozog geodetikuson (szabadon, erőmentesen), tehát ő öregszik többet, mint utazó testvére (akit rakétája hajtóműve fékezési és gyorsulási manőverekre kényszerít). Ha azonban egy olyan változatot tekintünk, amelyben az "egy helyben maradt" ikertestvér például végig a Föld felszínén tartózkodik, míg testvére "oda-vissza" utat tesz meg egy felfelé elhajított, majd a Föld felszínére visszaeső űrkabinban, akkor itt az utazó testvér mozog geodetikuson (szabadesésben, erőmentesen), tehát ő öregszik többet, mint a Földön maradt testvére (akit a talaj nyomóereje kényszerít a Föld felszínén maradni).

Pörgettyű és geodetikus precesszió

Mi a legtökéletesebb, legmegbízhatóbb iránytű, amely minden körülmények között a földrajzi (nem a mágneses!) északi irányba mutat? A newtoni mechanika szerint, ha egy pörgettyűre a gravitációs tér forgatónyomatékot fejt ki, a pörgettyű forgástengelye lassan elfordul (precesszál). Ha alkalmas felfüggesztéssel kiküszöböljük ezt a forgatónyomatékot, akkor a pörgettyű megőrzi forgástengelyének irányát a térben. Egy ilyen eszközt (amelyet gyro compass-nak, pörgettyűs iránytűnek neveznek) például a Sarkcsillag irányába állítva olyan iránytűhöz jutunk, amely északi irányát mindvégig megtartja. Hogyan egyeztethető ez össze a Foucault-inga síkjának elfordulásával? A kulcs az, hogy a pörgettyű azért alkalmas iránytűnek, mert "háromdimenziós objektum" [8]: miután megpörgettük, orientációjának beállására a térben nem szabunk ki kényszerfeltételt. Az eredetileg északi irányúra beállított Foucault-inga azért nem lenne alkalmas iránytűnek (hiszen pontosan erről is szól a Foucault-kísérlet!), mert lengésére kényszerfeltételt szabtunk: a lengő tömegpontnak a Föld érintősíkjában kell maradnia. Ugyanez igaz a délirányt jelző kordéra is: az irányt mutató nyíl nem fordulhat ki a Föld érintősíkjából. Félrevezető is a "délirányt jelző" elnevezés erre az egyébként zseniális találmányra: ha dél felé beállított nyíllal túl nagy területen tologatják, nem sokáig fogja tartani a helyes délirányt, a Földfelület görbültsége és a párhuzamos eltolás sajátosságai miatt (lásd korábban).10 Ebből a szempontból a Foucault-inga és a kordé is lényegileg "kétdimenziós objektumoknak" tekinthetők, amelyek a kétdimenziós Föld felület görbültségének feltérképezésére alkalmasak.

Vajon a kényszermentes pörgettyű, ez a "háromdimenziós objektum" nem alkalmas-e hasonló módon arra, hogy háromdimenziós terünk - illetve a négydimenziós téridő - görbültségére fényt derítsen? De igen: a "gyro compass"-t ugyanis csak a newtoni mechanika jósolja tökéletes iránytűnek; az általános relativitáselmélet szerint még egy szabadon lebegő, forgatónyomaték-mentes pörgettyű sem őrzi meg forgástengelyének irányát az állócsillagokhoz képest. Forgástengelye elfordulásának mértéke a pörgettyű által bejárt téridőtartomány görbültségére ad információt. A több évtizedes előkészület után néhány éve megvalósult GP-B (Gravity Probe - B) kísérlet speciálisan azt az esetet vizsgálta, milyen mértékben fordul el egy Föld körüli körpályára állított - erőmentesen, azaz geodetikuson mozgó - pörgettyű forgástengelyének iránya, a téridőnek a Föld által okozott görbültsége miatt. A jelenség neve geodetikus precesszió, hiszen a pörgettyű tömegközéppontja mindvégig geodetikuson mozog. Az elfordulás mértéke nagyon kicsi, a GP-B kísérletben választott 642 km-es keringési magasság esetén egy év alatt ~6,6 szögmásodperc¹¹ [9].

Érdemes kicsit tovább elidőzni a geodetikus precessziónál. A pörgettyű tömegközéppontja zárt görbét fut be a térben, egy teljes körbefordulás után mégsem ugyanabba az irányba mutat (az állócsillagokhoz képest). Vajon nem mond-e ez ellent a geodetikus tulajdonságairól korábban mondottaknak? Hiszen a pörgettyű tömegközéppontjának világvonala geodetikus vonal a téridőben; márpedig egy geodetikuson párhuzamosan végigvitt vektor mindvégig megőrzi irányát a geodetikushoz képest. Sőt, tovább sarkíthatjuk a problémát: cikkünk előző részének 4. ábrája azt mutatja, hogy ha zárt geodetikus görbén párhuzamos eltolással visszaviszünk egy vektort a kiinduló pontba, akkor pontosan fedésbe kerül a kiindulási vektorral. Miért nem ez történik (látszólag) a pörgettyű forgástengelyével? A választ a következő két megfontolás adja meg:

• A pörgettyű pályája ugyan zárt görbe a térben, de világvonala nem zárt görbe a téridőben. Nem várhatjuk automatikusan, hogy a (térbeli) kiindulási helyére visszatért pörgettyű forgástengelye a kiindulási helyzettel fedésbe kerüljön, hiszen a pörgettyű a téridőben nem tért vissza a kiindulási ponthoz, a visszatérési esemény és a kiindulási esemény nem "fedi egymást" a téridőben.
• A forgástengely a pörgettyű geodetikus világvonalához képest valóban megőrzi orientációját a téridőben. A pörgettyűt szállító, erőmentesen mozgó űrhajó utasa nem tapasztalna semmi rendelleneset: a forgástengely az erőmentesen lebegő űrhajó - mint térben lokalizált inerciarendszer - falának mindig ugyanarra a pontjára mutatna. Az űrhajó azonban nem erőmentesen mozog; szimmetriatengelyét egy alkalmas elektronika folytonosan abba az irányba kényszeríti, amelyben az űrhajóra rögzített távcső a referenciaként szolgáló távoli állócsillagot mutatja. Ez az a referenciairány, amelyhez képest a forgástengely nem őrzi meg orientációját. A dolog kulcsa tehát, hogy maga a referenciairány - azaz az űrhajó szimmetriatengelye - nem párhuzamosan tolódik el a geodetikus világvonal mentén.

  Egyéb példák

  A természetben még sok olyan jelenség van, amelyek értelmezésére a vektorok párhuzamos eltolásáról leírtak nagyszerű keretet szolgáltatnak. Ezek közül itt csak néhányat említünk meg, részletesebb levezetések nélkül.

  Nem csak görbült téridőben, hanem még sík téridőben is elfordul egy pörgettyű forgástengelye, feltéve hogy görbevonalú pályán visszük vissza a kiindulási helyre. Ez a newtoni mechanikában nem magyarázható jelenség - amelynek neve Thomas-precesszió, és alapvetően az idődilatációval hozható kapcsolatba - nem tévesztendő össze a fent tárgyalt geodetikus precesszióval, hiszen itt (1) sík téridőben mozog a pörgettyű tömegközéppontja, és (2) nem geodetikus (erőmentes) világvonalon, hanem gyorsulva. A Thomas-precesszió egyik nevezetes megnyilvánulása az atommag körül keringő elektron spintengelyének lassú elfordulása, amelynek mértéke a speciális relativitáselmélet matematikai apparátusával könnyen kiszámolható¹² [10]. Részletezés nélkül megemlítjük, hogy a Thomas-precesszió a Foucault-ingához teljesen hasonló módon tárgyalható, csak a pörgettyűt leíró perdületvektor gömbfelület helyett forgási hiperboloid felületén mozog, a négyessebesség-térben [11].

  Végül még egy példa, ezúttal az optika területéről. Tegyük fel, hogy egy üvegszálba lineárisan polarizált fényt csatolunk, és a szálat valamilyen módon elcsavarjuk, feltekerjük a térben, ügyelve arra, hogy a szálból kilépő fény a belépő fénnyel párhuzamos irányban haladjon tovább. Ekkor a kilépő fény polarizációs iránya nem lesz ugyanaz, mint a bemenő felületen becsatolt fény polarizációja [12]. A szögelfordulás mértéke a következő megfontolásokból számolható: nincs semmilyen külső hatás, amely az üvegszálban haladó fénysugár polarizációs irányát megváltoztatná. A fény azonban transzverzális hullám, így a polarizációvektornak ki kell elégítenie azt a kényszerfeltételt, hogy iránya minden pontban merőleges a sebességvektorra. A fénysugár sebességvektora mindvégig az üvegszál tengelye irányába mutat, nagysága pedig állandó. Összefoglalva: ahogy a szál csavarodik, a sebességtérben a sebességvektor végpontja egy gömbfelületen mozog, és a kezdő- és végállapot párhuzamossága miatt zárt görbét ír le. Eközben a polarizációvektor mindvégig érintője ennek a gömbfelületnek, és párhuzamosan tolódik el ugyanezen zárt görbe mentén. Ha tehát pontosan ismerjük a szál csavarodását, a sebességvektor pályája nyomon követhető a sebességtérben, a polarizáció teljes szögelfordulása pedig a Gauss-Bonnet-tételből közvetlenül kiadódik.

  Irodalom

  1. Budó Á: Mechanika. Tankönyvkiadó, Budapest, 1965.
  2. L. Foucault: Démonstration physique du mouvement de rotation de la Terre au moyen du pendule. Compt. Rend. 32 (1851) 135.
  3. H. Kruglak, L. Oppliger, R. Pitet, S. Steele: A short Foucault pendulum for a hallway exhibit. Am. J. Phys. 46/4 (1978) 438.
  4. F. W. Sears: Working model of a Foucault pendulum at intermediate latitudes. Am. J. Phys. 37/11 (1969) 1126.
  5. A. G. Rojo, D. Garfinkle: The parallelometer: a mechanical device to stűdy curvature. Can. J. Phys. 87 (2009) 615.
  6. http://www.hrasko.com/peter/full3.pdf
  7. E. F. Taylor, J. A. Wheeler: Exploring Black Holes. Addison Wesley Longman, Inc., 2000.
  8. D. E. Liebscher: Einstein's relativity and the geometries of the plane. Wiley-VCH, 1999.
  9. http://einstein.stanford.edu/
  10. E. F. Taylor, J. A. Wheeler: Téridőfizika. Typotex, Budapest, 2006.
  11. C. Criado, N. Alamo: Thomas rotation and Foucault pendulum under a simple unifying geometrical point of view. Int. J. Non- Lin. Mech. 44 (2009) 923.
  12. A. Tomita, R. Chiao: Observation of Berry's topological phase by use of an optical fiber. Phys. Rev. Lett. 57 (1986) 937.

  ________________________

  1. Ha az ingakísérlettel célunk kifejezetten a Föld forgásának bizonyítása, akkor ne az Egyenlítőn állítsuk fel a kísérleti apparátust: ott ugyanis - mint látni fogjuk - az inga lengési síkja a mi nézőpontunkból, azaz a Földhöz rögzített vonatkoztatási rendszerben nem fordul el.
  2. Másképpen: az egyensúlyi helyzet - az elhanyagolható centrifugális erőtől eltekintve - függőleges legyen.
  3. Más megfogalmazásban: az inga lengési síkja annyira lassan változik, hogy egy lengésen belül a tömegpont jó közelítéssel ugyanabban a síkban marad.
  4. Ez analóg azzal a kényszerfeltétellel, hogy a Foucault-inga egyensúlyi helyzete mindenhol merőleges a Föld felületére.
  5. A számítás meglehetősen bonyolult receptjét, azaz magát a Theorema Egregiumot itt nem részletezzük.
  6. A Riemann-féle elmélet felülről kompatibilis Gauss törekvéseivel: a görbületet leíró Riemann-tenzor ugyanis 2D felületek esetén egykomponensű mennyiséggé, skalárrá redukálódik, amelynek számértéke - konstans faktortól eltekintve - megegyezik a K Gauss-görbülettel.
  7. Itt csak annyit jegyzünk meg, hogy a párhuzamos eltolás definíciója magasabb dimenziójú esetekben legegyszerűbben egy algebrai egyenletrendszerrel adható meg, amelyben az úgynevezett Christoffel-szimbólumok szerepelnek.
  8. Hogy hogyan, arról az elmélet alapegyenlete, az (itt nem részletezett) Einstein-egyenlet ad számot.
  9. Ez esetben tehát nem eredményként kapjuk meg, hogy geodetikus mentén eltolva egy vektor megtartja az irányát, hanem fordítva, a geodetikust így definiáljuk.
  10. Egy példa a nagyságrend érzékeltetésére: a Földet sima gömbnek tekintve, a kordét a mai Kína határán körbetolva a kiindulási pontba, a nyíl teljes elfordulása a Gauss-Bonnet-tétel szerint δ = (Kína területe)/(a Föld sugara)² ≈ 13°.
  11. A számadatból tehát látható, hogy a "gyro compass" minden gyakorlati célra nyugodtan tekinthető tökéletes iránytűnek.
  12. A Thomas-precesszió a Foucault-inga elfordulásához is ad járulékot, ez azonban kimutathatatlanul kicsi, egy nap alatt mintegy 10^-6 szögmásodperc.