BÉKÉSY GYÖRGY FIZIKA EMLÉKVERSENY

Härtlein Károly
BME Fizikai Intézet

A verseny kiemelt témái a névadó munkásságából adódóan az akusztika, a fénytan és a villamosságtan. A verseny elméleti és kísérleti részből áll. A méréseknek kiemelt szerepet szánunk, ezért az első napon elméleti előadást és kísérleti bemutatót is tartunk. A versenyre elsősorban a téma iránt érdeklődő tanulók jelentkezését várjuk, a 9., 10. és 11. évfolyamokról.

A középiskolai tanulók 11. évfolyama számára 12. alkalommal meghirdetett Békésy György Fizika Emlékverseny ebben az évben is a megszokott feszes, de nem barátságtalan rend szerint zajlott le a meghirdetett és betartott alábbi program szerint.

Péntek május 20.

• 14 óra érkezés a Puskás Technikumba, regisztráció
• 14 óra 30 írásbeli feladatrész
• 17 óra 30 írásbeli vége
• 17 óra 30 és 18 óra között indulás a szálláshelyre (Táncsics kollégium)

Szombat május 21.

• 8 óra Puskás Technikumban az írásbeli eredmények ismertetése és a kísérlet megkezdése,
• 8 és 10 óra között a döntőbe nem jutottak számára Tóth Pál, a Fizibusz vezető tanára tartott előadást
• 10 óra gyakorlati feladatok védése
• 12 óra szünet
• 13 óra eredményhirdetés, feladatmegoldások ismertetése

Az írásbeli feladatok

1. feladat kitűző: Nagy Márton, Sopron
Egy mechanikai hullám egyik közegből a másik közegbe lép át. Melyek változnak meg az alábbi, hullámmozgást jellemző fizikai mennyiségek közül?

2. feladat kitűző: Wiedemann László, Budapest
Adott egy U = 2000 V feszültségre feltöltött, elszigetelt síkkondenzátor. Egyik lemeze rögzített, a másik vízszintes irányban, önmagával párhuzamosan és az első lemezre merőlegesen elmozdulhat. Ehhez vízszintesen egy D direkciós erejű finom rugó csatlakozik, amelynek másik vége rögzített. A lemez elmozdulása a rugó hosszának változását eredményezi. Kezdetben a rugó feszítetlen, a lemezek távolsága d, egy lemez felülete A és tömege m. Minden súrlódástól eltekintünk.

1. A rugóval kapcsolt lemez rögzítését feloldva mekkora lesz a lemezek maximális távolsága, ha feltöltés után a feszültségforrást a kondenzátorról lekapcsoljuk?
2. Milyen mozgást végez a szabad lemez?
3. Mennyi idő alatt következik be a mozgó lemez maximális elmozdulása?

A lemezek között működő merőleges vonzóerő:

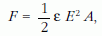
ahol ε = 8,86 · 10^-12 As/Vm, E a lemezek közti homogén elektromos tér térerőssége, A egy lemez felülete.

Adatok: d = 1 cm, A= 100 cm², D = 0,1 N/m, a mozgó lemez tömege m = 10 g.

3. feladat kitűző: Kotek László, Pécs
Nem hullámzó, mély tóban egy pontszerű fényforrás halad függőlegesen lefelé v = 0,8 m/s sebességgel. A víz törésmutatója n = 4/3. Mekkora sebességgel mozog vízszintes irányba a víz felszínén lévő fényfolt határa?

4. feladat kitűző: Härtlein Károly, Budapest
Az európai szabvány szerint működő videokamerák másodpercenként 25 képet rögzítenek. Milyen fordulatszámoknál látszik állónak annak a fúrógépnek a tokmánya, amelyik három pofával szorítja meg a befogott csigafúrót?

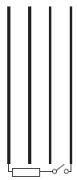
5. feladat kitűző: Kotek László, Pécs

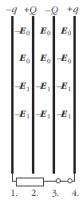
Négy darab azonos felületű, egymással szemben lévő, párhuzamos fémlemezt az ábrán látható módon elhelyeztünk, a középső fémlemezeknek +Q és -Q töltést adtunk, a szélső fémlemezek pedig töltetlenek. A lemezek azonos távolságra vannak egymástól, ez a távolság a lemezek méreteihez képest kicsi. a) Mennyi töltés halad át a fogyasztón, ha a kapcsolót zárjuk? b) Mekkora hő fejlődött a fogyasztón, ha ismert, hogy két szomszédos fémlemezből kialakított síkkondenzátor kapacitása C?

Ami nem állt a diákok rendelkezésére

Ami a versenyen nem állt a diákok rendelkezésére, itt egy-egy lehetséges megoldás is megtekinthető.

A 2. feladat megoldása
A lemezek vonzása következtében a rugóval kapcsolt lemez elmozdul. Mivel a kondenzátor töltése változatlan marad, azért bármely helyzetben az E térerősség változatlan. Ez három összefüggésből következik:

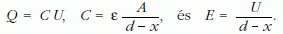
Ezekből

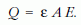
Tehát az E térerősség a pillanatnyi lemeztávolságtól független állandó. Mivel a lemez elmozdulásával a kondenzátor kapacitása növekszik (csökken a lemezek távolsága), a kondenzátor energiája a

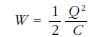
képlet alapján csökken, ezért a lemezek között működő vonzóerő munkája a kondenzátor energiájából táplálkozik:

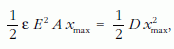
tehát

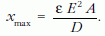
A mozgásra nézve azt állítjuk, hogy a lemez harmonikus rezgőmozgást végez. Ennek belátására írjuk fel bármely t időre nézve a mozgásegyenletet:

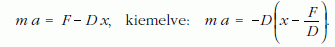
Bevezetve az

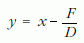
új változót, az előbbi mozgásegyenlet y-ban harmonikus rezgőmozgást ír le eltolt egyensúlyi helyzettel:

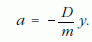
Ezek szerint

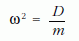
körfrekvenciájú harmonikus rezgést végez a rugóhoz kötött lemez. A legnagyobb kitérést fél periódus alatt éri el a lemez az indulástól számítva.

A képletekbe való behelyettesítés után a legnagyobb kitérés x_max = 3,5 cm, ω = 10 s^-1, T/2 = 0,314 s.

A legnagyobb kitérés úgy is számítható, hogy felírjuk a munkatételt, vagy az energiamegmaradás törvényét a rugóból és a mozgó lemezből álló rendszerre.

Más megfontolás: mozgás közben a térerő munkája által folyton cserélődik az energia a rugó potenciális és a kondenzátor elektrosztatikai energiája között.

A 3. feladat megoldása
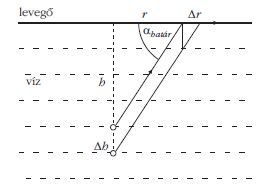
Legyen a fényforrás h távolságra a víz felszínétől! Ebben a pillanatban a víz felszínén egy kör alakú fényfolt van. A kör r sugarát a teljes visszaverődés α_határ határszögének ismeretében határozhatjuk meg.

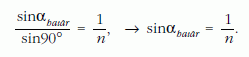
Innen a kör sugara

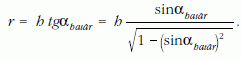
Az α_határ szögre kapott kifejezést behelyettesítve:

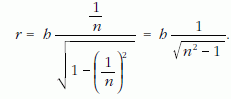
Legyen a fényfolt határának sebessége u! Tegyük fel, hogy a fényforrás Δt idő alatt Δh-val mozdul el, azaz v sebességére igaz, hogy v = Δh/Δt. Eközben a kör sugara r -ről r+Δr értékre növekszik. A háromszögek hasonlóságából:

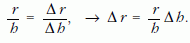
A keresett u sebesség:

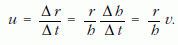
A kör r sugarára kapott kifejezést behelyettesítve:

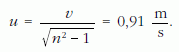
A 4. feladat megoldása
A megoldáshoz ismerni kell a stroboszkopikus hatást, megoldásként nem egy fordulatszámot kapunk, hanem egy sorozatot. A legalacsonyabb fordulatszám, amelynél állónak látszik a fúrógép tokmánya:

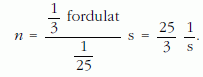
E fordulat egész számú többszörösei is megoldások.

Az 5. feladat megoldása
a) 1. megoldás. A kapcsoló zárása után legyen az 1. számú lemez töltése -q, ekkor a 4. számú lemez töltése +q, és q töltés halad át a fogyasztón a kapcsoló zárása után. A q töltés abból a feltételből határozható meg, hogy az 1. számú lemez és 4. számú lemez között a potenciálkülönbség zérus. Határozzuk meg az egyes töltött lemezek által létrehozott térerősségeket! Legyen a Q töltésű lemez által keltett mezőt jellemző térerősség E0, a q töltésű által keltetté pedig E₁, ahol:

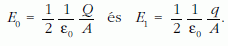
Kihasználva, hogy az 1. számú lemez és 4. számú lemez között a potenciálkülönbség zérus:

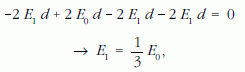
innen és a térerősségek kifejezéséből:

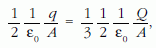
amiből a fogyasztón áthaladó töltés:

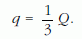
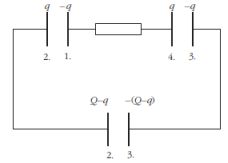
a) 2. megoldás. Rajzoljuk át a kapcsolást, figyelemq be véve, hogy a 2. számú lemez és 3. számú lemez két kondenzátor alkotásában vesz részt!

Használjuk fel a töltésmegmaradást, továbbá azt, hogy zárt hurokban a feszültségek előjeles összege zérus, azaz

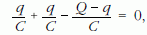
amiből a keresett töltés:

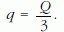
b) A ΔW fejlődő hőt a rendszer kezdeti W₁ és végállapotbeli W₂ energiáinak különbsége adja.

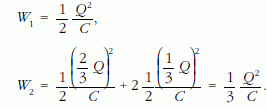
A fejlődő hő:

Kísérleti feladat

kitűző: Härtlein Károly, Budapest Az asztalon található rudak segítségével határozd meg a longitudinálisan terjedő hullám terjedési sebességét alumíniumban!

Eszközök:

A pálcák több féle módon hozhatók rezgésbe. Ennek megfelelően álló hullámok keletkeznek, amelyek frekvenciája függ a rúd geometriai méretétől, és az anyagminőségtől. Más és más hangon fog megszólalni ugyanaz a pálca, ha longitudinális vagy transzverzális, esetleg csavarási állóhullámot gerjesztünk. A számítógépen futtatható egy program (SpectraLab), amely segítségével hangfrekvenciás tartományban lehet frekvenciát mérni. A spektrumanalizáló szoftver valós idejű hanganalízist, frekvencia- és intenzitásmérést tesz lehetővé. Elindításakor az alapbeállítások segítségével a függőleges tengelyen a hang erősségét, a vízszintes tengelyen a frekvenciát lehet leolvasni.

Ezen kívül a számítógép desktopján (asztal) található egy film, amelyben megtekintheted az alumínium pálca „énekeltetésének” módját. Itt leírásokat is találhatsz a pálcákon kialakuló állóhullámokról.

Az egyik kézzel hüvelyk- és mutatóujj-jal kell tartani a pálcát. A másik kéz mutató- és hüvelykujját kell gyantaporral bekenni. Ezzel a kézzel – hosszanti irányban dörzsölve – kell rezgésbe hozni a pálcát.

A rendelkezésre álló idő 1 óra 50 perc. A mérés elvégzése után a zsűri, a kísérőtanárok és a döntőbe nem jutott diákok előtt, kiselőadás formájában kell ismertetni a mérést!

A mérés során bármilyen könyv és számológép használható! Jó munkát!

Megoldás

A mérés elvégzéséhez a versenyen szokásos módon segítségként további információkat találhattak a versenyzők. Filmeket, amelyek a megszólaltatást mutatták be, és mivel nem törzsanyag a pálcák rezgései és a rajtuk kialakuló állóhullám, erről leírást. (http://jedlik.phy.bme.hu/bekesy2011)

Egy 500 és egy 750 mm hosszú pálca állt rendelkezésre. A pálca rezgésbe hozásával hallható hangot gerjesztünk, amelynek frekvenciáját kell megmérni. Ezen kívül meg kell mérni a pálca hosszát, így már csak a jól ismert

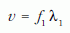
képletbe – f₁ a mért frekvencia, λ₁ az állóhullám hullámhossza – kell a mért adatokat behelyettesíteni.

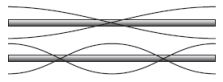
A pálca megszólaltatása akkor lesz sikeres, ha tartó kezünkkel a csomópontot fogjuk, és gerjesztő kezünkkel a duzzadó helyet gerjesztjük. Mindkét pálcán az alapmóduson kívül az első felharmonikust is meg lehetett szólaltatni.

<>

Az eredményhirdetésnél kiderült, hogy az első helyet Broda Balázs, a miskolci Földes Ferenc Gimnázium tanulója, Gregánné Hursán Zsuzsanna és Zámborszky Ferenc tanítványa szerezte meg, míg Sápi András, a hódmezővásárhelyi Bethlen Gábor Református Gimnázium tanulója, Nagy Tibor tanítványa lett a második és Pölöskei Péter Zsolt, a szigetszentmiklósi Batthyány Kázmér Gimnázium tanulója, Juhász Róbert tanítványa a harmadik helyet érdemelte ki.