Fizikai Szemle honlap |
Tartalomjegyzék |
Gombkötő Balázs, Kornis János
BME Fizikai Intézet, Fizika Tanszék
A Fizikai Szemle többször is foglalkozott már hasábjain a holográfiával. Először maga Gábor Dénes írt cikket (1966/10), majd mások mutatták be a holográfia körébe tartozó kutatásaikat (például 1968/2), többek között a röntgen-holográfiát is két alkalommal (1997/7 és 2005/3). 2000 júniusában Gábor Dénes születésének 100. évfordulóján külön is foglalkozott a Szemle a témával (2000/6), ekkor jelent meg a Nobel-díj átadáson tartott beszéd, illetve előadás is. Mindezidáig azonban nem jelent meg cikk a holográfia digitális és számítógépes változatáról, holott ez az ág is hamar követte a lézerek megjelenését, és 1994 óta a digitális CCD-kamerák elterjedésével, valamint az informatika addig és azóta bekövetkezett fejlődése révén a reneszánszát éli.
Elsőként röviden áttekintjük a holográfia történetét és lényeges elemeit, hogy látható legyen a digitális világba vezető út. Amint azt Gábor Dénes is leírta, két hullám interferenciamezője, azaz az intenzitáseloszlás, képes tárolni egy tárgyról szóródott hullám valamilyen értelemben "teljes" információtartalmát, ha a másik referenciahullám egyszerű és reprodukálható, például sík vagy gömbhullám, és ha monokromatikus, kellően koherens hullámokat alkalmazunk. Ezt már Gábor elődei is tudták, azonban arra nem gondoltak, hogy ez a mintázat diffrakciós elemként használva létre is hozhatja a tárgyhullámot, illetve annak eléggé pontos mását. 1947–48 táján a kor lehetőségeit alkalmazva kísérletileg demonstrálták is az elv helyességét, majd a lézerek megjelenésével, kihasználva annak nagyfokú koherenciáját, Lieth, Upatnieks és Denisyuk révén új erőre kapott a holográfia.
Ekkor már nagyobb fényintenzitás állt rendelkezésre, ténylegesen különválasztható lett a tárgy- és referencianyaláb, nagyobb méretű tárgyakról is lehetett hologramot készíteni, egy lemezre akár többről is, előtérbe kerülhettek a diffúz felületű tárgyak, szó szerint látványos eredmények születtek, és a rövidebb expozíciós idők révén a méréstechnika és az elektronikus detektálás felé is lehetett nyitni.
A jelenből visszatekintve érdemes megjegyezni, hogy a holográfia egyetemi oktatásában még ma is a Gábor Dénes 1966-os cikkében is fellelhető egyszerű egyenletek és szemléltető ábrák használatosak: a néhány sorban megadható komplex algebrai alapegyenletek a felvételről és a rekonstrukcióról, valamint az egyetlen pontforrás síkreferenciával készült hologramján megjelenő Fresnel-zónarendszer, illetve a rajta végbemenő fényszóródás. Szintén fontos, hogy Gábor már a kezdetektől hangsúlyozta a holográfia információtárolási módját és jelentőségét, amelyet befogadva a ma közembere számára is érthető lehet az őt leginkább foglalkoztató kérdés egy szép hologram láttán, nevezetesen "mi van akkor, ha eltörik".
Az elvek után essék szó a gyakorlatról is! Hologramot készíteni macerás: rezgésmentes környezet kell, lehetőleg erősebb lézer, jó felbontású fotoemulzió vagy másfajta rögzítő anyag, a nedves kidolgozáshoz kevésbé barátságos vegyszerek, végül türelem és technológiai fegyelem. Ma már persze házi "laborokban" is készíthetők jó hologramok, az internet ebben is eligazítja az érdeklődőt. Ha magát a hologramlemezt tekintjük, transzmissziós hologramok és néhány centiméteres tárgyak esetén a felbontóképességükkel szembeni elvárás nem igazán nagy. Ha a tárgyat a méretéhez képest jelentősen eltávolítjuk a lemeztől, valamint a referencia is kis szög alatt – majdnem "inline" – érkezik a lemezhez, akár 5-10 mikron méretű fényérzékelő elemek is megengedhetők, azaz a fényképezésnél is használatos fekete-fehér negatívok vagy diapozitív filmek is megfelelőek lehetnek – ezt használta Gábor is első kísérleteiben.
Még szélsőségesebb esetben még nagyobb pixelméretű eszköz is alkalmazható lett volna, mint a hatvanas- hetvenes évek TV kamerái (például vidicon cső). Érdekes módon az első "digitalizált hologramot" 1967-ben J. W. Goodman és munkatársai [1] mégsem így készítették, hanem egy kidolgozott, kész amplitúdóhologram kinagyított részét végigszkennelték egyetlen fényérzékelővel, azaz utólagos analóg-digitális konverzióval. A felvett adathalmazt egy PDP-6 típusú, 160 kB-nak megfelelő memóriával rendelkező számítógéppel képesek voltak digitálisan rekonstruálni, azaz a tárgy-, képsíkba Fouriertranszformálni. Egy 1980-as cikkben még mindig a szkennelős eljárást látni, noha 1974-ben az elektronikus szemcsekép interferometriában – amit másképp a hasonlóságok okán TV holográfiának is neveztek – már használtak TV/video kamerákat, és az első CCD érzékelő-mátrix is ekkortájt jelent meg laboratóriumi szinten. Ilyen kamerák kereskedelmi forgalomba 1987 táján kerültek, ezt követően 1994- ben bukkant fel először a holografikus rács direkt kamerás felvétele [2].
A digitális holográfia másik vonulata szintén 1967- ben jelent meg [3]. Számítógépes forrásból származó adatokkal oszcilloszkóp képernyőjén jelenítettek meg holografikus rácsozatot, amelyet filmre fényképezve kész volt a számítógéppel generált hologram, akár egy elképzelt tárgyról is. Mind hologram generálásánál, mind digitalizált hologram számítógépes rekonstrukciójánál megjelent a számítási kapacitás kérdése. Már 1976-ban 256× pixeles adatokat lehetett diszkrét Fourier-transzformálni nagygépeken, a "CCD-forradalom" idején pedig ez a kapacitás már PC-ken is elérhető volt. A digitális hologramok készítésének és alkalmazásának célja már a kezdetektől is az volt, hogy kihasználják jelentős információtartalmát. Vonzó lehetőség volt háromdimenziós modellek valós térbeli megjelenítése számítógéppel generált hologramok révén (ez nem terjedt el), illetve adatok utólagos kinyerése akár mérési céllal digitalizált hologramokból. A generált hologramok megjelenítésénél nagy áttörés volt a kis méretű térbeli fénymodulátorok (SLM, lásd digitális projektorokban) megjelenése, mivel tisztán elektronikus eszközként itt is nélkülözni lehet a filmek nedves kidolgozását, ráadásul valós időben változtatható a megjelenített hologram.
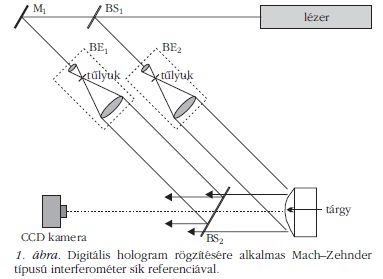
Az 1. ábra egy tipikus optikai elrendezést mutat digitális hologramok felvételére centiméteres tárgyak esetén. A Mach–Zehnder típusú interferométerben két kitágított és kollimált síkhullám terjed, és a BS2 nyalábegyesítő után közel azonos irányból érik el a kamerát. A 2. ábra egy digitális hologram intenzitáseloszlását mutatja, amit a csupasz kamera "lát". Ezen a példán emberi szemmel könnyen észrevehetők a kissé ferde és ívelt interferenciacsíkok a rajtuk ülő véletlen szemcsés fázissal, amely a diffúz felületű 2-3 cm-es tárgy nyalábjának köszönhető. Ez az immár digitális holografikus rácsozat az elsődleges információhordozónk a továbbiakban. A szintén digitális rekonstrukcióhoz ezt az eloszlást immár amplitúdóeloszlásnak tekintve és megszorozva a referencia gömbhullám fáziseloszlásával (vagy jelen esetben sík referenciahullám esetén gyakorlatilag azzal sem) elindíthatjuk a fény terjedését/diffrakcióját szimuláló számítást. Az 1. ábra geometriája mellett Fresnel-diffrakcióra, azaz diszkrét Fresnel-transzformációra van szükség, amelyet a gyors Fourier-transzformáció (FFT) alkalmazásával pillanatok alatt el lehet végezni. Ha a fényterjesztést a kamera-tárgy távolságban lévő síkdarabkára végezzük, a két konjugált elsőrendű diffrakciós folt közül az egyik éles vetített képet fog adni a kérdéses tárgyról, ahogy az a 3. ábrán látható. Középen az intenzív áthaladó nyaláb, annak túloldalán pedig egy virtuális képnek megfelelő első rendű nyaláb látható. Ellenkező előjelű távolságba diffraktáltatva a fényt a két első rendű nyaláb szerepet cserél.
A 3. ábrán látható valós vetített kép az első rendű elhajlásban elsőre semmilyen térbeliséget nem mutat. A rekonstrukció távolságát változtatva azonban a képélesség változik, azaz a tárolt fázisinformáció révén fókuszálható a kép! Ha tehát több, a kamerától különböző távolságban elhelyezett tárgyról készítünk egyetlen digitális hologramot, a rekonstrukcióban egyszerre csak egy tárgy lesz éles, a többinek szükségszerűen életlen képét látjuk. Ezt használják ki a digitális holografikus mikroszkópiában, ahol egy pár köbmilliméteres térfogatról készül egyetlen digitális hologram az 1. ábráétól eltérő, még egyszerűbb elrendezésben, majd a digitális rekonstrukció "végigpásztázza" a térfogat síkmetszeteit, kiemelve az ott tartózkodó szóró objektumokat, például szennyező szemcséket, mikroorganizmusokat. Áramló folyadék térfogatáról időben kissé eltolva több felvétel is készíthető, így a benne lebegő szemcsék elmozdulása egyenként követhető az egész térfogatban, és a folyadék áramlása feltérképezhető három dimenzióban.
A fenti példákban a fókuszálhatóságot, a mérés utáni (!) pásztázás lehetőségét használják ki, azonban dacára annak, hogy a kamerával rögzített digitális hologram egy valós adatmátrix, a digitális rekonstrukció eredménye mindig komplex értékű, azaz a 3. ábrán látható intenzitáshoz fázis is tartozik. Ennek önmagában a numerikus számítás sajátságai miatt általában nincs érdekes képe, azonban a digitális holográfia másik népszerűbb ipari alkalmazása, az interferometria épp e fázisnak köszönheti létét. Ha egy terhelhető tárgyról a terhelés előtt és után is készítünk egy-egy digitális hologramot, vagy a mozdulatlan tárgyról kissé eltérő körülmények között készítünk digitális hologramokat (például eltérő hullámhosszon vagy eltérő referenciairánnyal), akkor ezek rekonstruált képét összeadva vagy kivonva (digitálisan interferáltatva) máris szerephez jut a fázis. A két komplex amplitúdó eloszlás különbségének intenzitását és fázisát mutatja a 4.a és b ábra. Ez utóbbi direkt fáziskép a hagyományos analóg holográfiában nem látható, itt azonban közvetlenül hozzáférhető, és látványos tartalommal bír. Míg a hagyományos holografikus interferometriában az interferogramoknak csak az intenzitása hozzáférhető, így az alak vagy alakváltozás iránya/előjele nem látható egyértelműen, a direkt fázisképen látható a fázisváltozás iránya is. Megjegyezzük, hogy a fázis ilyen egyértelmű jelentéséhez az is kell, hogy a három diffrakciós rend a rekonstruált képen szétváljon, azaz ne fedjenek át. Teljesen in-line elrendezésben ez a zavaró hatás már nem elhanyagolható, és a holografikus mikroszkópiában is külön foglalkozni kell az ikerkép hatásával vagy kiküszöbölésével.
Szót kell még ejtsünk egy izgalmas részterületről, digitális hologramok optikai rekonstrukciójáról térbeli fénymodulátor (SLM, Spatial Light Modulator) segítségével. Kamerával felvett vagy számítógéppel generált digitális hologramok egyaránt készíthetők, illetve átalakíthatók amplitúdót vagy fázist moduláló eszköz részére. Folyadékkristályos vagy mikrotükrös SLM-ek is alkalmasak lehetnek erre a célra, ám eltérő karakterisztikájukat (például nem a digitális jellel arányos fázistolás) többnyire kompenzálni kell. Megfelelő beállítások mellett az SLM-re adott digitális hologram miatt az SLM a valós lézernyaláb számára holografikus rácsként fog viselkedni, és a továbbterjedő fényben létrejönnek az ilyenkor megszokott elhajlási rendek. Ideális esetben az ikerkép akár ki is küszöbölhető, a "rendes" kép pedig a digitális hologramtól függően lehet valós vagy akár virtuális is. Ily módon az első esetben mód van egy tárgy holografikus megvilágítására, a másik esetben pedig a hagyományoshoz hasonló 3D látvány előállítására. Az előbbire mutat példát az 5. ábra. Jobb oldalon a megvilágított tárgy látható, bal oldalon pedig a megvilágító első rendű nyaláb ikerképe egy hasonló négyzetes tárgyról. (Jelen esetben az első rendű képek mindketten fókuszált valós képek, mivel a digitális hologram Fourier-típusú, azaz "végtelenben" lévő tárgy szintén "végtelenben" lévő ikerképpel.) A képen látható megvilágításhoz már nem szükséges azon tárgy jelenléte, amelyről a digitális hologram készült. Akár adathordozón, akár az interneten hordozhatóvá válik a digitális hologramban tárolt rengeteg információ, így akár hasonló tárgyak összehasonlító távmérése is lehetséges.
Az előbb bemutatott előnyök mellett természetesen további előnyei és hátrányai is vannak a digitális holográfiának. A digitális kamerák a detektált intenzitást nagyfokú linearitással alakítják elektromos jellé, az expozíciós idők másodperc alattiak, az exponálás paraméterei jól megválaszthatók az optimális eredmény érdekében, azonban könnyen találkozhatunk elektronikus zajokkal, továbbá egyetlen akár 10 megapixeles digitális hologram információtartalma is eltörpül egy jó analóg holograméhoz képest. A két technika összeházasításával is találkozhatunk a holografikus adattárolásban, ahol a hologramokat ugyan (utólagos kémiai kezelést nem igénylő) fényérzékeny tárolóanyagba rögzítik, azonban a beíráshoz SLM-et, a kiolvasáshoz digitális kamerát használnak, és e digitalizálás számos előnyét ki is használják. Végezetül digitális holográfiával sokkal "fájdalommentesebben" demonstrálható, hogy mi történik, ha egy hologramot eltörünk. Ha digitális adatunk csak egy kis részterületét rekonstruáljuk, természetesen az egész tárgy képét visszakapjuk, csak kisebb felbontásban, kevésbé részletesen.
Összegezve, a digitális holográfia a maga egyszerűségével és képességeivel mára megtalálta a neki való alkalmazási területeket, és biztosak lehetünk benne, hogy a jövőben is hallani lehet majd róla.