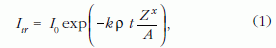
Fizikai Szemle honlap |
Tartalomjegyzék |
Pozsgai Imre
Richter Gedeon R.T.
A Fizikai Szemle 2011/6 számában Bencze Gyula Rutherford tevékenységét méltatta abból az alkalomból, hogy Rutherford száz évvel ezelőtt fedezte fel az atommagot. E kimagasló tudós tevékenysége Szalay Sándoron keresztül közvetlenül és gyorsan hatott a magyarországi magfizikai kutatásokra. Ennek részleteire és Rutherford aktualitására Berényi Dénes világított rá a Fizikai Szemle ugyanennek a számában közölt második cikkben. Bár az első írásban meglepően sok Rutherford- tanítvány nevét olvashatjuk, a másodikban azt írja Berényi Dénes Szalay Sándorról: "Nem túlzunk, akkor, ha azt állítjuk, hogy munkatársairól, együttműködő partnereiről nem sokkal rövidebb névsort lehetne összeállítani, mint Rutherford esetében."
A debreceni fizikusképzésről már egyszer megemlékeztem a Fizikai Szemlében Berényi Dénes tevékenysége kapcsán [1], de most újra megteszem, mert mély nyomokat hagyott bennem és valamennyi évfolyamtársamban. Szalay Sándor radioaktivitást és atomfizikát oktatott nekünk fizikushallgatóknak a Debreceni Egyetem Kísérleti Fizikai Intézetében. Ezen túlmenően Raics Péterrel tudományos diákköri munkát is végeztem nála.
Az alább ismertetendő elektronszórási mérések [2-4] szolgáljanak annak bizonyítékául, hogy a debreceni oktatás mennyire befolyásolta gondolkodásmódomat a későbbi, külső körülmények ellenére is.
Az egyetem elvégzése után az MTA Műszaki Fizikai Kutatóintézetében kezdtem dolgozni. Ott a transzmissziós elektronmikroszkópot használhattam volna "rendeltetésszerűen", azaz képek előállítására, de engem sokkal jobban érdekeltek azok az atomfizikai folyamatok, amelyekhez előképzettségemet Debrecenben szereztem meg. Így került látókörömbe az elektronszórás, elektronsugaras röntgen mikroanalízis és elektronenergia veszteségi analízis a transzmissziós elektronmikroszkópban, továbbá a mikro-röntgen fluoreszcens analízis a pásztázó elektronmikroszkópban. Bár vékony minták lokális tömegvastagságának meghatározásáról fogok írni, de ennek hátterében az elektronszórás rendszámfüggése, illetve a rendszámfüggés feszültségfüggése áll.
Azt a feladatot tűztem magam elé, hogy vákuumpárologtatott vékonyrétegek lokális tömegvastagságát (sűrűség és lineáris vastagság szorzata) határozzam meg a transzmissziós elektronmikroszkópban (TEM) a besugárzó elektronnyaláb vékony mintában fellépő abszorpciójának mérésével. Az exponenciális sugárgyengülésre számos példát láttam az atomfizikában. De az irodalomban talált adatok alapján [5] a központi nyaláb intenzitásának közvetlen mérése Faraday-kalickával az elektronmikroszkóp képernyőjének síkjában számos kristályos rétegen (Sb, Ag, Au, Bi, Cu stb.) az exponenciálistól eltérő, anomális sugárgyengülést mutatott. Az ok a minták kristályos szerkezete miatt fellépő Bragg-reflexiók, amelyek többszörös szórás révén erősen megváltoztatták a központi elektronnyaláb intenzitását.
Az elektronok szóródása nemcsak a minta vastagságától függ, hanem a szóró atomok rendszámától is. Ez utóbbiról csak annyit lehetett tudni, hogy 60 kV-nál kisebb gyorsító feszültségeknél és kis szórási szögtartomány (α < 4 · 10–3 rad) esetén lineárisan függ a rendszámtól (Lenz-közelítés [6]), majd magasabb gyorsító feszültségeknél a rendszám kitevője 4/3 (Moliere-közelítés [7]), végül nagy gyorsító feszültségeknél és nagy szórásiszög-tartományban a szóró atomok rendszámának négyzetével arányos Rutherford-közelítéssel írható le.
A kérdés az volt, hogy a rendelkezésemre álló maximális 100 kV-os gyorsító feszültségen érvényes-e a Rutherford-közelítés, vagy ha nem, akkor hogyan határozzam meg a kitevő pontos értékét. A maximális gyorsító feszültség használatát a kedvező leképezési lehetőségek tették szükségessé.
Egy tudományosan érdektelen, de gyakorlatilag fontos peremfeltétel az volt, hogy az elektronmikroszkópon csak olyan változtatásokat volt szabad végeznem, amelyek rövid idő alatt helyreállíthatók voltak és a sok felhasználós mikroszkóp működését nem korlátozták.
A Columbo-filmekhez hasonlóan az elején "lelövöm a poént": az első 100 kV-os transzmissziós elektronmikroszkóppal még nem, de a másodikkal, amelyen már 200 kV-os gyorsító feszültséget lehetett beállítani, elértem azt a pontot, amikor a Rutherford-közelítést alkalmazni lehetett. Ennél a pontnál az elektronoknak olyan nagy a kinetikus energiájuk, hogy az atommagot árnyékoló elektronburok átlátszóvá válik számukra, a mag hatása teljesen érvényre jut és a négyzetes rendszámfüggés jó közelítésnek bizonyul. Mint később látni fogjuk, ennek gyakorlati jelentősége abban áll, hogy a több anyagon végzendő rendszám-kalibrációt el lehet hagyni és a feladat egyetlen anyagon végzendő tömegvastagság- kalibrációra redukálódik.
A Bragg-reflexiók zavaró hatásának elkerülésére nem a központi nyaláb mérését választottam, hanem olyan nagy szögtartományban integráltam a transzmittált elektronintenzitást (Itr), amely már a Bragg-reflexiókat is tartalmazta. Ez az integrált intenzitás már exponenciális gyengülést mutatott a rétegvastagság függvényében. A fentiek összefoglalhatók a következő egyenletben [8]:
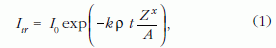
ahol Itr a mintán átmenő, nagy szögtartományban integrált elektronnyaláb intenzitása; I0 a mintát besugárzó elektronnyaláb intenzitása; k arányossági tényező; ρ sűrűség; t lineáris mintavastagság; ρt tömegvastagság; Z rendszám; A atomsúly; x a rendszám ismeretlen kitevője.
A kalibráló rétegeket vékony (10-20 nm) szénhártyára vittem fel volfrám szálról vagy csónakból vákuumpárologtatással 5 · 10–6 mbar nyomáson. A rétegek tömegvastagságát rezgőkvarcos vastagságmérővel monitoroztam. A vastagságokat Noran gyártmányú energiadiszperzív röntgenspektrométerrel is ellenőriztem és csak azokat a rétegeket használtam fel kontrasztmérésre, amelyekre a röntgenintenzitás lineáris függést mutatott a vastagsággal. Az elektronmikroszkópiában kontraszt alatt a
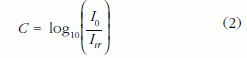
kifejezést értik.
A kontrasztméréshez a nagy szórásszöget úgy biztosítottam, hogy az objektív blendét visszahúztam a sugármenetből.
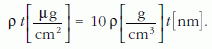
A minták tömegvastagsága és lineáris vastagsága között a következő összefüggés áll fenn:
A rétegek közül a Ti, Ag és Au polikristályosak, a Ge amorf volt. A 100 kV-os JEOL 100U transzmissziós elektronmikroszkópon végzett méréseknél még Al, Fe, Sb és Bi is szerepelt a kalibráló minták sorában, de az ottani méréseredmények meggyőztek arról, hogy a 200 kV-os mikroszkópon végzett rendszámkalibrációhoz négy anyag is elegendő lesz.
A transzmittált elektronintenzitást nem lehetett olyan műszerrel mérni, amelyet széles szögtartományban mozgatok az integráláshoz, erre az elektronmikroszkóp nem ad lehetőséget. A JEOL 100U és a 200 kV-os Philips CM20 transzmissziós elektronmikroszkópok nagyon különböző megoldásokat kívántak meg az elektronáram szög szerinti integrálására. Ezek részletes ismertetése túlmegy e cikk keretein, viszont az idézett cikkekben megtalálható [2, 3]. Mindössze a 200 kV-os mikroszkópon alkalmazott megoldás sémáját mutatom az 1. ábrán.
Az ábrán S -sel jelzett kis ernyő eredetileg az automatikus expozíció céljait szolgálta, különösen olyan esetekben, amikor a V-vel jelzett nagy képernyőn az intenzitáseloszlás nagyon inhomogén, például diffrakciós képek felvételekor. Az eredeti konstrukciót az ábrán szaggatott vonal mutatja: a kis ernyőről lefolyó áram egy logaritmikus erősítőn keresztül a fénymérő (E) irányába folyt. Az eredeti csatlakozást elvágtuk, BNC-csatlakozót szereltünk fel, és a kis ernyőt egy előfeszítő tápforráson keresztül Keithley 601C típusú elektrométerhez (A) kötöttük. A tápforrás +63 V-os feszültsége arra szolgál, hogy a kis ernyőből kilépő szekunder elektronokat visszatartsa. A mérések befejezésével a kis képernyőnek a logaritmikus erősítővel és a fénymérővel való eredeti kapcsolatát BNC-csatlakozó segítségével állítottuk helyre.
A kontraszt lineáris vastagságtól vagy a tömegvastagságtól való mért függését a 2. ábra mutatja négy elemre. Meghatározva a 2. ábrán látható egyenesek S meredekségét
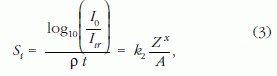
ahol k2 = k log10 e = 0,43429 k, a következő értékeket kaptam:
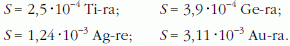
A (3) egyenlet logaritmálásával kapjuk, hogy
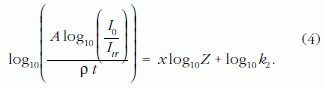
A (4) egyenlet bal oldalát a log10Z függvényében ábrázoltam (3. ábra), hogy a rendszám kitevőjét megkapjam.
A legkisebb négyzetek elve alapján történt illesztésből a következő numerikus értékekhez jutottam:
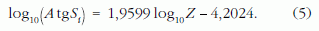
A (4) és az (5) összehasonlításából következik, hogy a k2 = 6,3 · 10–5, így k = 1,44 · 10–4. Ezért az (1) egyenlet a következő alakban írható fel:
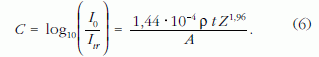
A (6) egyenlet csak egykomponensű rétegek vastagságának meghatározását teszi lehetővé, amelynek gyakorlati jelentősége viszonylag kicsi. Többkomponensű rétegek esetén a transzmittált elektronintenzitás függeni fog a vizsgált terep kémiai összetételétől is. Mint korábban megmutattam, a ci koncentrációk segítségével a következő átlagolás végezhető el [2]:
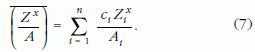
A (7) formula segítségével az egykomponensű rétegekre nyert (6) formula általánosítható többkomponensű rétegekre is:
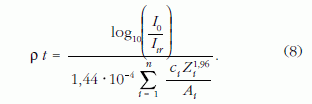
A (8) formula szerint egy minta ρt tömegvastagsága meghatározható kontrasztmérés segítségével, amennyiben a vizsgált pont kémiai összetétele (ci ) ismert. Az esetleg ismeretlen kémiai összetétel meghatározható az elektronmikroszkóphoz csatolt röntgen- vagy elektron-spektrométer segítségével.
A (8) formulában a rendszámnak 1,96-os kitevője kísérleti hibán belül megegyezik a Rutherford-közelítés 2-es exponensével. Ez lehetőséget ad arra, hogy egyszerűsítsük a tömegvastagság meghatározását a TEMben azáltal, hogy a kitevőt 2-nek választjuk a rendszámfüggésre a (6) egyenletben és a rendszám-kalibrációt elhagyjuk. Egyetlen arányossági tényezőt (k2 a (3) egyenletben) kell csak meghatároznunk 4-5 ismert vastagságú rétegen. Tételezzük fel, hogy az integrált transzmittált elektronintenzitást (Itr) germánium rétegeken (vagy más közepes rendszámú elemen, például Fe, Co, Ni, Cu, Zn) mérjük a 20-100 µg/cm2 tömegvastagság tartományban.
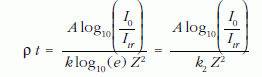
összefüggés miatt k2-re a következőket kapjuk:
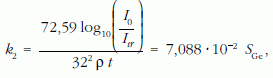
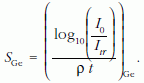
Így a (6)-nak megfelelő formula germánium rétegekkel való kalibráció esetén
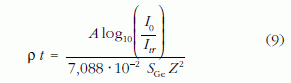
alakot ölt egykomponensű rétegekre.
Többkomponensű rétegekre a (9) formula a következőképpen általánosítható:
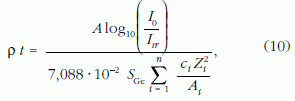
ahol ci, Zi és Ai a többkomponensű réteg komponenseinek koncentrációja, rendszáma, illetve atomsúlya.
A (9) formula helyességét ellenőriztem a 2. ábrán látható Ti, Ag és Au rétegek adatain. A Z1,96 ((6) formula) és a Z2-tel számolt tömegvastagságok ((9) formula) különbsége Ti rétegekre 1,5%, Ag rétegekre 1,52% és Au rétegekre 3,5% volt.
A (6) formula szerint az elektronszórás rendszámfüggésének kitevőjére 200 kV-os gyorsítófeszültségen kapott érték (1,96) nagyon közel áll a Rutherford-közelítés által adott 2 értékhez. Korábbi, 100 kV-os gyorsítófeszültségen végzett, más típusú mérésekben a szórás rendszámfüggésének kitevőjére 1,8-et kaptam [2]. Ez késztetett annak elemzésére, hogy mivel magyarázható a rendszám kitevőjének feszültségfüggése.
Induljunk ki az (1) alapegyenletből és hasonlítsuk össze a (11) egyenlettel, amely a jelenség egy másik oldalról való megközelítéséből adódik:
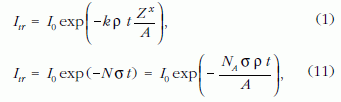
ahol N az egységnyi térfogatban lévő atomok száma, NA az Avogadro-szám, σ a teljes szórási hatáskeresztmetszet.
Az (1) és (11) összehasonlításából látható, hogy Zx viselkedését a teljes szórási hatáskeresztmetszet, σ határozza meg. A teljes szórási hatáskeresztmetszet a rugalmas (σe) és rugalmatlan (σi) szórási hatáskeresztmetszetek összegeként adódik:
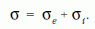
Vizsgáljuk meg külön a rugalmas és a rugalmatlan tagot! A rugalmas szórás differenciális hatáskeresztmetszete [9]:
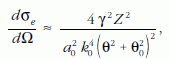
ahol 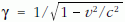 relativisztikus korrekció, a0 a
Bohr-sugár, k0 = 2π/λ a hullámszámvektor, θ a szórási
szög,
relativisztikus korrekció, a0 a
Bohr-sugár, k0 = 2π/λ a hullámszámvektor, θ a szórási
szög,
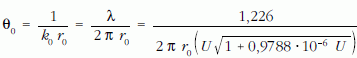
árnyékolási tényező, r0 az árnyékolási sugár és U a gyorsító feszültség.
A rugalmas szórási hatáskeresztmetszet a θ0 árnyékolási tényezőn keresztül függ a gyorsító feszültségtől. Ha θ0 = 0, akkor elhanyagoljuk az elektronburoknak az atommagra gyakorolt árnyékoló hatását és (12)-ből a Rutherford-közelítéshez jutunk el, amelyben a szórás Z2-es függést mutat. A Rutherford-közelítés nagy θ szórási szögekre jobban teljesül, mert az árnyékolásért felelős θ0 (12)-ben elhanyagolhatóvá válik.
Amikor a gyorsítófeszültség nem olyan nagy, hogy az árnyékolási tényező elhanyagolható lenne, akkor az árnyékolási sugár a Thomas-Fermi-modell szerint:
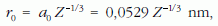
és (12)-ben a rugalmas szórási hatáskeresztmetszet Z4/3-os rendszámfüggést mutat (lásd a bevezetőben említett Moliere-közelítést). A k0 hullámszámvektor fontos szerepet játszik az árnyékolásban, ezért σe függ az elektronok λ hullámhosszától, következésképpen a gyorsítófeszültségtől is.
A rugalmatlan szórás függését a gyorsítófeszültségtől hasonlóképpen mutathatjuk meg. A rugalmatlan szórás differenciális hatáskeresztmetszete [10]:
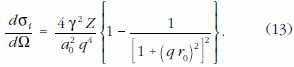
Itt 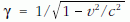 relativisztikus korrekció,
q a szórásvektor,
relativisztikus korrekció,
q a szórásvektor, 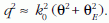
A (13) egyenlet közvetlenül is tartalmazza az r0 árnyékolási sugarat és implicite a k0 hullámszámvektort, ahogy a (12) egyenlet is. Így semmi kétség nincs afelől, hogy a σi rugalmatlan szórási hatáskeresztmetszet is függ a gyorsító feszültségtől. A diszkussziót azzal kezdtem, hogy a Zx viselkedését a σ határozza meg, így a σ feszültségfüggésének bizonyításával azt bizonyítottam (amit kísérletileg is kaptam), hogy az elektronszórás rendszámfüggésének x kitevője függ a gyorsítófeszültségtől.
Röviden és szemléletesen úgy összegezhetjük a fenti magyarázatot, hogy egyre növekvő gyorsítófeszültségnél egyre kevésbé árnyékolják le az atommagokat saját elektronjaik.
A vékonyrétegek elektronsugaras röntgen mikroanalízisében nagy jelentősége van a tömegvastgaság ismeretének, ugyanis a vékony mintákban elektronbesugárzással kiváltott röntgensugárzás intenzitása (Irtg,i ) lineárisan függ a minta tömegvastagságától. Egy n-komponensű mintára:
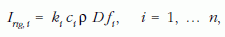
ahol ki arányosági tényező, amely ismert vastagságú, egykomponensű rétegek segítségével meghatározható, ci az i -edik elem koncentrációja, ρ a minta sűrűsége, D a minta lineáris vastagsága, ρD a minta tömegvastagsága, fi korrekciós tényező, amely a röntgensugárzás mintában való abszorpcióját és fluoreszcenciáját veszi figyelembe, értéke vékony rétegekre 1.
Egy n-komponensensű mintánkra n darab egyenletünk van, de az ismeretlenek száma n+1 (a minta tömegvastagsága ρt az (n+1)-edik ismeretlen). Ha nem ismerjük a tömegvastagságot, akkor a koncentrációk 100%-ra való normálására kényszerülünk, ami sok pontatlanságot okozhat kis koncentrációjú komponenseknél a nem mért vagy pontatlanul mérhető könnyű elemek miatt. Végső soron az együttes röntgenmérés és elektronintenzitás-mérés azt eredményezi, hogy az ismeretlenek és a rendelkezésre álló egyenletek száma megegyezik. A koncentrációk öszszegének 100%-tól való eltérése jól használható a mérések pontosságának jellemzésére, továbbá felhívhatja a figyelmet a vékonyréteg kritériumtól való eltérésre ( fi ≠ 1) és szükség esetén a röntgensugárzás mintában történt abszorpciójának a korrekciójára.
Összefoglalva elmondhatjuk, hogy 200 kV-on vagy ennél nagyobb gyorsítófeszültségeken az elektronok szórására teljesül a Rutherford-közelítés, azaz a Z2-es rendszámfüggés. Ezt a tényt jól lehet hasznosítani a transzmissziós elektronmikroszkópban végrehajtott tömegvastagság-mérésben és kvantitatív elektronsugaras mikroanalízisben.