
Fizikai Szemle honlap |
Tartalomjegyzék |
Stonawski Tamás
Báthori István Református Gimnázium
és Kollégium, Nagyecsed
A gyerekszobában a valóság kicsinyített modelljeit fedezhetjük fel: a mackó, a babaszoba, a kisautó, a kisvasút mind a valóságtól eltérő, apró méretűek. Amikor a gyermek egy játékautóval játszik, óriásnak érzi magát, akár Gulliver a mesebeli Liliputban, és könnyedén emelgeti játékautóit. Vajon, ha tényleg ilyen nagyra nőnénk, és valóságos autókkal játszanánk, akkor a valódi autók a játék során hasonlóan viselkednének-e, mint a modell-társaik (1. ábra)? Vajon könnyebbnek éreznénk-e a felemelt valódi gépkocsikat, mint a modell-autókat, és esetleg össze is tudnánk azokat roppantani?
Hogy a feltett kérdésekre válaszolhassunk, kiválasztottunk egy Volvo C70 típusú modellautót, és kikerestük a Volvo katalógusából (2. ábra) a gépkocsi gyári adatait. A játékautó szélességét, hosszúságát és lemezvastagságát tolómérővel, a tömegét digitális mérleggel (3. ábra) mértük meg (1. táblázat).
A lemezvastagságon kívül a geometriai arányok rendre megegyeztek: 1:43, ami elterjedt arány a kisautók körében. Ezt az arányt a gyártó is feltüntette az "alvázon" (4. ábra). Ettől az aránytól a visszapillantó tükör felfogatásánál tértek el a könnyebb önthetőség érdekében.
Az autók oldallemezeinek vastagságára vonatkozó arány viszont jóval eltér a 43-tól, 1-nél kisebb értéket vesz fel. Ha kiszámoljuk a λ = 43-ra vonatkozó lemezvastagságot a kiskocsi esetére, akkor 0,02 mm-t kapunk, ami egy háztartási alufólia vastagságának felel meg. Tehát az óriásoknak nagyon óvatosan kellene emelgetni a személyautóinkat! Egy gyermek körülbelül 1–6 N erővel szorítja meg a kiskocsit, ami az óriás esetében λ3-szörös lenne: 79 507–477 042 N, ami megfelel annak, mintha egy tank menne keresztül a járművön (10. ábra).
 |
 |
Természetesen érthető, hogy a játékgyárak a használati igénybevételek miatt a geometriai arányoktól eltérő, jóval nagyobb lemezvastagságot választják.
A megnövekedett lemezvastagság is magyarázza a tömegek arányának λ3-től való eltérését:
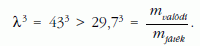
A kiskocsi tömegét pusztán a geometriai arányok figyelembevételével 20,8 grammosra várjuk, ami harmada a mért értéknek.
A valóságos autók ütközéseit rengeteg körülmény befolyásolja: a fékezés, a kerekek és a talaj közötti súrlódási együttható különbözősége (ami a gépjármű forgását, pörgését okozhatja), az ütközési sebesség, az autó gyártmánya, tömege, műszaki állapota, de az sem mellékes, hogy mivel ütközik.
Az autógyártás első évtizedeiben az autóipar vezetői nem nagyon figyeltek fel a rengeteg halálos áldozatot is követelő közúti balesetekre. Az 1950-es években került sor az első töréstesztre, amit a magyar származású Barényi Béla (1907–1997) végzett el. Az ő nevéhez fűződik a nem deformálódó utastér, a nyugalmi állapotban rejtett ablaktörlő és a biztonsági kormányoszlop feltalálása, de a gyűrődési zóna megfelelő kialakítása is [2].
A valóságos autók ütközése nem kizárólagosan rugalmatlan vagy rugalmas, az ütközési folyamatokban mindkét típusú ütközést felfedezhetjük.
A személygépkocsik lemezvastagsága sem azonos, a karosszéria kiemelt helyein vastagabb és merevítőkkel van ellátva. A kiskocsi lemezvastagsága sem egyenletes, az öntési eljárásnak megfelelően helyfüggő lehet.
Az összehasonlítandó autók anyagai is különbözőek: a valódi autó hengerelt, mélyhúzott acéllemezből készül, míg a vizsgált játékautó anyaga spiáteröntvény (más néven zamak), cink-alumínium ötvözet, így azonos jellegű erőhatásokra akár teljesen eltérően reagálhatnak.
A valóságos és a modellautó ütközéseinek összehasonlítása céljából törésteszteket végeztünk a kiskocsikon (5. ábra), majd összehasonlítottuk a valódi autók töréstesztjével.
A 6. ábrán egy személyautó 64,4 km/h-val történő frontális ütközését láthatjuk [3]. Ezt a sebességet az állandó nagyságú nehézségi erő által létrehozott gyorsítással is elérhetjük abban az esetben, ha 16,2 méter magasságból vastag betonra ejtjük az autót (egy képzeletbeli speciális ejtőcsőben, hogy forgás nélkül essen, frontálisan ütközzön és a visszapattanás után ne végezzen tranziens mozgásokat):
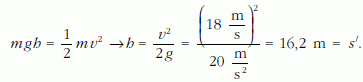
Ha a kiskocsival is szeretnénk hasonló ütközési kísérleteket végezni, az ejtési magasság:
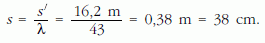
Ejtési kísérletek 38 cm magasságból
Az ejtési kísérletet egy szobában végeztük el, ahol kerámia-járólapra ejtettük a kiskocsit, a vonalzóval előre bejelölt 38 centiméteres magasságból. A kísérletet egy 120 frame/s időbeli felbontású kamerával vettük fel. Az ütközés után az autó többször megpördült, és majdnem annyi időt töltött a levegőben, mint a zuhanáskor. A kísérlet után az öntvényanyagban deformációt nem tapasztaltunk, csak a jobb első lámpa alatt sérült meg a festékréteg (7. ábra).
Ütközési kísérletek vízszintes talajon
A töréstesztet vízszintes mozgásnál is elvégeztük. Nagy sebességgel nekilöktük a kiskocsit a kerámialapnak, amiről videofelvételt is készítettünk, majd a mozgást kielemeztük egy ingyenes video-analizáló programmal [4]. A szoftver segítségével meg tudtuk határozni a kiskocsi sebességét az ütközés pillanatában. Ez a sebesség 75 cm/s volt, ami a valóságos autónál 116,1 km/h-nak felel meg. Ismét megvizsgáltuk a kiskocsit, méreteiben nem változott, deformációt nem tapasztaltunk, csak a festékréteg sérült meg a bal alsó lámpa alatt (8. ábra).
Konklúziók
Ahogy a kísérletek is mutatták, a játékautók nem roncsolódnak össze még nagyobb sebességű ütközések során sem. A valódi autók pedig már kisebb sebességű ütközések esetén is hajlamosak a deformációkra.
Bár a vizsgált kiskocsi és a valóságos autó mozgását geometriai hasonlóságuk miatt (ugyanabban az aerodinamikai közegben) jól le lehet írni, a komplex mechanikai rendszerek ütközéseinél önmagában a geometriai arány az ütközések kimenetelének leírásához már nem bizonyult elegendőnek. Nem véletlen, hogy az autóipar, költséget nem kímélve, valóságos méretű autókkal végzi el az ütközési kísérleteit.
Óriás lett a matchboxom!
De mi történne, ha egy reggelen nem csak Gulliver nőne óriássá, hanem modellautónk is? Vajon ez a monstrum milyen paraméterekkel rendelkezne? Hogyan nézhetne ki egy olyan gépjármű, aminek nemcsak a méretei, hanem lemezvastagsága is követné a modellautónk geometriai arányait? Számítsuk ki a lemezvastagságot:
λ · 1,3 mm = 43 · 1,3 mm = 55,9 mm.
Számítsuk ki a tömeget:
λ3 · 63 g ≈ 5 t.
Ezek az adatok nagyon közelítik egy harckocsi adatait (9. ábra):
Vessük össze a kiskocsi adatait a harckocsi "gyári" adataival (2. táblázat)!
A geometriai hasonlósági arány szinte minden vizsgált paraméternél megegyezik, így az óriássá nőtt kisautó ütközései is sokkal jobban közelítenék a harckocsik ütközéseit. Persze a tankok egymással való ütközéseinél az utasok biztonsága nem kiemelten fontos tényező, a harckocsik szinte egyetlen nem deformálódó "utastérből" állnak.
Ha tehát a valóságban találkozik egy "felnagyított" modellautó és egy valódi személyautó, az megfelel egy tank és egy személykocsi végzetes találkozásának (10. ábra).
<>
A modellautók mért adatainak a valóságos autók paramétereivel való összehasonlítása és kiértékelése mindenképpen hasznosak lehetnek a fizikaoktatásban és a gépjárművezetésben is. A 11. osztályos tanulók többsége a jogosítvány megszerzése előtt áll (a vizsgált osztályban a tanulók 30%-a KRESZ-tanfolyamra járt), ezért a tanulók motiváltsága igen kedvező a gépjárművekkel kapcsolatos problémák megoldásában. A kísérletek során könnyen lehetett mozgósítani a közepes képességű diákokat is, a felhasznált digitális környezet szintén motiváló erőként hatott a diákokra. Az autóvezetés és a fizika kapcsolatát maguk a tanulók fedezték fel, és az előbbieken kívül sokkal több összefüggést is észrevettek a munka során (a gépkocsi tömege és fogyasztása közötti kapcsolat, miért nem lehet 100 km/h a tankok sebessége … stb.). A tanulók többsége már rutinszerűen alkalmazta a kinematika és a dinamika összefüggéseit, a grafikonelemzés is sikeres volt, a hasonlóságot, mint matematikai fogalmat már korábbról ismerték, a tömegekre alkalmazott arányosság pedig átvezette őket a fizika tantárgy témakörébe. A kísérletben részt vevő tanulók remélhetőleg körültekintő gépjárművezetők lesznek, és a fizika sem csak az utakon jut majd az eszükbe.