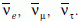NEUTRÍNÓOSZCILLÁCIÓ, LEPTOGENEZIS, NEUTRÍNÓGYÁRAK

Fényes Tibor
MTA ATOMKI, Debrecen

A neutrínók a leptonok közé tartozó, elektromosan semleges elemi részecskék. Mindhárom leptoncsaládnak megvan a maga neutrínója, így vannak elektronneutrínók (υ_e), müonneutrínók (υ_µ) és tauneutrínók (υ_τ), valamint létezik mindegyiknek antineutrínó párja is: 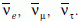Ha a Z a sebesség irányát jelenti, a neutrínókra a spin Z komponense J_Z = -1/2 (balkezes), az antineutrínókra J_Z = +1/2 (jobbkezes).

A neutrínók sajátságai sok tekintetben egyediek. Rendkívül kicsi a tömegük, kisebb mint bármelyik más lepton vagy kvark elemi részecskéé. Például az elektronneutrínó tömege < 2 eV, míg az elektroné 0,511 MeV. A neutrínók kölcsönhatása anyaggal rendkívül kicsi. A reaktorból származó antineutrínók közepes szabad úthossza kondenzált anyagban ~10¹⁶ km (~1000 fényév), aminek az az alapvető oka, hogy sem az erős, sem az elektromágneses kölcsönhatásban nem vesznek részt. Ugyanakkor a neutrínók az általunk ismert Világegyetem leggyakoribb anyagi részecskéi, csak a fotonok száma nagyobb náluk.

A neutrínófizika fejlődése során számos meglepetéssel szolgált és alapvetően megtermékenyítette a magfizikát és részecskefizikát. Nem sokkal azután, hogy Pauli 1931-ben feltételezte a neutrínók létét, Fermi 1933–34-ben megalkotta a β-bomlás elméletét, amelynek szerves részét képezik a neutrínók. Mindmáig ez a β-bomlás alapvető elmélete. A neutrínófizikai eredmények igen lényeges szerepet játszottak a gyenge kölcsönhatás vektor-axiálvektor jellegének felderítésében, a gyenge semleges áram felfedezésében (abban, hogy a gyenge kölcsönhatást nem csak az elektromosan töltött W ^±-bozonok, hanem a semleges Z-bozon is közvetíti), az egyesített elektrogyenge-elmélet kidolgozásában, a nukleonszerkezet tanulmányozásában. A neutrínófizikának újabban már gyakorlati alkalmazása is van, detektáltak geoneutrínókat, távoli szupernóva-robbanásból származó neutrínókat, szerepük van a kozmikus sugárzás eredetének felkutatásában.

A neutrínófizika egyik legutóbbi, lényeges felismerése a neutrínóoszcilláció volt. Ez azt jelenti, hogy a neutrínóknak repülésük során változik az "ízük", azaz az elektron-, müon- és tauneutrínó összetételük. Az oszcilláció alapvető oka az, hogy a neutrínóknak kicsi, de különböző tömegük van és a különböző ízű neutrínók a neutrínók tömegsajátértékeinek különböző keverékeiként állnak elő. Az ízváltozást mára már mind a nap- és reaktorneutrínós, mind az atmoszférikus és gyorsítós neutrínóvizsgálatok egyértelműen mutatják (Gonzalez-Garcia, Maltoni [1], Mohapatra és mts. [2], Particle Data Group [3, 4], Fényes [5]).

A jelen közlemény első része vázlatosan ismerteti a neutrínóoszcilláció elméleti értelmezését, valamint összegzi a neutrínóoszcilláció kutatásában elért legfontosabb eredményeket és a még nyitott kérdéseket. A második rész a fejlődési irányokat tárgyalja, az első generációs szupernyaláb és reaktorneutrínó kísérleteket, valamint a második generációs szupernyaláb, β-nyaláb és neutrínógyár terveket.

A neutrínóoszcilláció kvantummechanikai elmélete

A neutrínók oszcillációja elméletileg is értelmezhető. A feltevés szerint a neutrínók különböző fajtái ízsajátállapotban 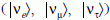állnak elő, illetve semmisülnek meg, de ezek tömeg-sajátállapotok 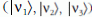szuperpozíciói.

A kapcsolat mátrix alakban kifejezve:

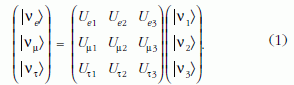
Az U-mátrixot Pontecorvo (1957, 1958), illetve Maki–Nakagawa–Sakata (1962) ismerte fel először, így róluk nevezték el.

Ha minden neutrínó tömeg nélküli lenne, a tömeg- és ízsajátállapotok egybeesnének és nem lenne neutrínóátalakulás sem. Az (1) összefüggés feltételezi, hogy a neutrínóknak van tömege.

Ha a neutrínóknak van tömege, a υ₁, υ₂, υ₃ tömegállapotokban lévő neutrínók – mint később látni fogjuk – eltérő frekvenciával haladhatnak. Így fáziskülönbség alakulhat ki közöttük a megtett távolság függvényében, ami neutrínó-ízváltozáshoz (oszcillációhoz) vezethet.

Az (1) mátrix analóg a kvarkkeveredési mátrixszal, ahol a kísérleti adatok egyértelműen mutatják a mátrix unitér jellegét [4]. (Unitér egy U-mátrix akkor, ha U†U = 1 és UU† = 1, ahol 1 egységmátrixot jelöl. Az U† mátrix úgy képezhető U-ból, hogy a sorokat és oszlopokat megcseréljük és minden elem komplex konjugáltját képezzük.) Az unitér mátrix elemei parametrizálhatók három keveredési szöggel: θ₁₂, θ₁₃, θ₂₃ és egy δ fázissal. (Ha a neutrínók Majorana-részecskék, további két fázis lehet.) A θ szögek rotációs transzformációnak felelnek meg az 1. ábra szerint. A keveredési mátrix parametrizált alakja a következő:

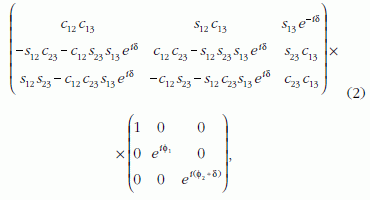
ahol c_ij ≡ cosθ_ij és s_ij ≡ sinθ_ij. Dirac-neutrínók esetében a (2) kifejezésnek csak az első mátrixa veendő figyelembe, Majorana-neutrínóknál mind a kettő. A δ-t Dirac-fázisnak, a φ₁-t és φ₂-t Majorana-fázisnak nevezik. Dirac-neutrínóknál a balkezes neutrínó és a jobbkezes antineutrínó két különböző részecske. A Majorana-neutrínóknál a neutrínó azonos az antirészecskéjével 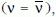azaz csak egy 1/2 spinű neutrínó van, de két különböző alállapot: υ_bal és υ_jobb. Jelenleg még nem eldöntött kérdés, hogy melyik elképzelés valósul meg a természetben.

A tárgyalás egyszerűsítése érdekében tekintsünk csak két ízsajátállapotot (υ_e, υ_µ) és két tömeg-sajátállapotot (υ₁, υ₂). Ekkor az U mátrix a következőképpen alakul:

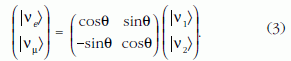
Az unitér transzformáció csak egy szabad paramétert tartalmaz, a θ keveredési szöget.

Ha az elektronneutrínó t = 0 időben keletkezett p impulzussal, az időtől függő hullámegyenlet megoldása szerint síkhullámként terjed és t idő múlva az állapota a következő lesz:

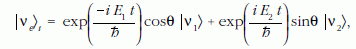
ahol

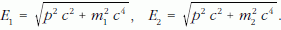
Itt nem részletezett levezetés alapján közel fénysebességgel terjedő neutrínónyalábra a következő kifejezés nyerhető:

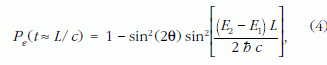
ahol

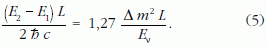
Itt P_e (t=L /c ) annak a valószínűsége, hogy a neutrínónyaláb t idő múlva elektronneutrínó lesz, P_e(t)+P_µ(t) = 1; Δm² = 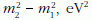egységben; L a neutrínónyaláb forrásától mért távolság méterben; E_υ ≈ pc MeV-ben; ħ a redukált Planck-állandó, c a fénysebesség vákuumban.

Bevezethető az oszcilláció hossza: L_oszc, e távolságon áthaladva P_µ ugyanazt az értéket veszi fel:

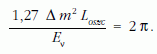
A P(υ_e → υ_e) és P(υ_e → υ_µ) valószínűségek változását az L/L_oszc függvényében a 2. ábra mutatja. A (4) és (5) összefüggések lehetőséget adnak a Δm² tömegnégyzet-különbség és a θ keveredési szög meghatározására.

A neutrínóoszcilláció meggyőző bizonyítást nyert a KamLAND reaktor-antineutrínó kísérletekben. A 3.b ábra az elektron-antineutrínó hozzájárulást mutatja a reaktorneutrínók fluxusához az L/E_υ függvényében.

Az eddigiekben a neutrínóoszcillációt vákuumban tárgyaltuk. Ha a neutrínók anyagban haladnak, más fáziskülönbségek alakulnak ki (Mikheyev–Smirnov–Wolfenstein-effektus). Anyag jelenlétében a υ_e → υ_µ oszcilláció valószínűsége erősen megnő, míg a υ_µ ↔ υ_τ oszcilláció a Föld és Nap anyagában gyakorlatilag úgy zajlik le, mint vákuumban. (Részletesebben lásd például az [1] és [4] közleményekben.)

A neutrínóoszcillációra vonatkozó eredmények összegzése

Összegezve a neutrínókra vonatkozó kísérleti és elméleti eredményeket, a következők szűrhetők le.

A Napból és reaktorból (L ~ 180 km) származó neutrínók, valamint az atmoszférikus neutrínók vizsgálata is meggyőzően mutatja a neutrínók ízváltozását. Továbbá erős érv szól a mellett, hogy gyorsítóknál (L ~ 250 és 735 km) is fellép a jelenség (L a neutrínók megtett útja).

A keveredési mátrix elemei és tömegnégyzet-különbségek (Gonzalez-Garcia, Maltoni [1]).

A neutrínókeveredési mátrix elemei (3σ szinten) a következők:

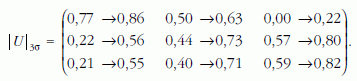
Ellentétben a kvarkokkal, a neutrínóknál erős keveredés lép fel.

Ha az unitér keveredési mátrix szögeit θ_ij-vel, a neutrínó tömegnégyzet-különbségeket 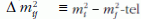-tel jelöljük, 3σ szinten a kísérletek által megengedett tartományok a következők:

A neutrínók tömegnégyzet-spektruma a 4. ábrán szemléltethető. Ha csak három neutrínó létezik, akkor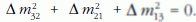

Mivel a neutrínóoszcillációs kísérletek csak a tömegnégyzet különbségekre érzékenyek, a neutrínók tömegeire többféle elrendezés lehetséges.

Normál hierarchiánál (m₁ < m₂ << m₃) 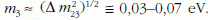A legkönnyebb neutrínó tömege nincs meghatározva. Ha m₁ << m₂, akkor m₂ 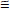0,009 eV. Fordított hierarchiában (ahol m₁ 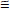m₂ >> m₃) 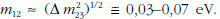Ekkor az m₃-ról csak azt tudjuk, hogy jóval kisebb, mint m₁ és m₂.

Kvázidegenerált neutrínók esetén (amikor mindhárom m² körülbelül egyenlő) a neutrínótömegek jóval nagyobbak a tömegkülönbségeknél.

A három könnyű neutrínó tömege a legkönnyebb tömeg függvényében az 5. ábrán látható.

CP-invariancia sérülése. A kvarkok esete. A három kvarkcsalád keveredési mátrixában jelentkezik egy δ fázisparaméter, ami a CP-invariancia sérülését eredményezi (C töltéskonjugációra, P paritásra utal.) Ez annak a következménye, hogy az exp(iδ) fázistényező megjelenik a hullámfüggvényben exp(iωt+iδ) alakban. Ez nem invariáns az időmegfordításra, ha δ ≠ 0 és δ ≠ π. Mivel a CPT-invariancia fennáll, ezért ha a T- (idő-) invariancia sérül, a CP-nek is sérülni kell. A CP-invariancia ilyen sérülésének felismeréséért Kobayashi és Maskawa elnyerte a (megosztott) 2008-as Nobel-díjat. A δ fázis felelős minden CP-sérülési jelenségért a standard modell ízváltozási folyamataiban. A CP-invariancia sérülését a kísérletek a semleges K- és B-mezonok bomlásában egyértelműen mutatják. Minden CP-invariancia sérülése konzisztens a Kobayashi–Maskawa-mechanizmus előrejelzésével [4]. Világegyetemünk döntő részben anyagból és nem antianyagból áll, noha az Ősrobbanásban ezek egyensúlyban voltak. A CP-sértés felismerése hozzájárul az anyag-antianyag aszimmetria megértéséhez (bariogenezis), még ha nem is elég a teljes magyarázathoz [3–5].

A neutrínók esete. A kvarkkeveredési mátrixhoz nagyon hasonló (2) neutrínókeveredési mátrix szintén tartalmaz egy δ Dirac-fázist. (További φ₁, φ₂ CP-sértő fázisok jelenléte a (2) mátrixban a Majorana-részecskék speciális sajátságainak következménye.) A CP-megmaradást sértő fázisok jelenleg nem ismertek. A leptonoknál fellépő CP-invarianciasérülés felderítése hozzájárulhat a világunk anyag-antianyag aszimmetriájának megértéséhez (leptogenezis). Ez a jövőbeni neutrínókutatások egyik legfontosabb célkitűzése.

A Dirac-, illetve Majorana-fázisokra információ szerezhető úgy, hogy a neutrínók és antineutrínók túlélési valószínűségét mérik nagy távolságban a forrásoktól, ehhez azonban nagy intenzitású "neutrínógyárak" szükségesek.

Nyitott kérdések

A biztató eredmények ellenére a terület még távolról sem tekinthető lezártnak. A következő kérdések megválaszolása a jövő feladata.

A neutrínók Majorana- vagy Dirac-részecskék? Ezt alapvetően fontos lenne tudni mind a leptonoknál fellépő CP-invarinaciasérülés, mind a neutrínótömegek eredetének megértése szempontjából. A neutrínóoszcillációs vizsgálatok erre sajnos nem adnak választ. E kérdés eldöntésére legjobb esélye a neutrínó nélküli kettős β-bomlás vizsgálatának van [4].

Milyen numerikus értékei vannak a Pontecorvo–Maki– Nakagawa–Sakata-mátrix elemeinek, továbbá a neutrínók tömegsajátértékeinek (υ₁, υ₂, υ₃)? Különösen fontos lenne tudni, hogy mennyi a θ₁₃ értéke, ami jelenleg igen nagy hibával ismert. A (2) neutrínókeveredési mátrixban a sinθ₁₃ együtt szerepel az e^-iδ fázistényezővel, így hatással van a CP-sértő effektusok nagyságára.

Szükséges lenne meghatározni a 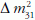előjelét és eldönteni, hogy normál vagy fordított hierarchia valósul meg a természetben (4. ábra).

Valószínű, hogy – a neutrínókon kívül – a CP-invariancia sérülése a töltött leptonoknál is jelentkezik. Vizsgálandó, hogy létre jönnek-e a természetben a µ⁺ → e⁺ γ és hasonló folyamatok, sérül-e a leptoncsaládszám megmaradása.

Létezik-e "steril" neutrínó, ami nem vesz részt a Standard modell gyenge kölcsönhatásában, nem csatolódik a Z-bozonhoz? A Los Alamosban elvégzett LSND (Liquid Scintillator Neutrino Detektor) kísérletben 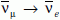oszcillációra 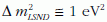értéket nyertek, ami nem illik a három neutrínócsalád képbe. Értelmezéséhez új, "steril" neutrínót kellene bevezetni. A kérdés tisztázására a Fermi-laboratóriumban MiniBooNE néven kísérleteket végeztek, amelyek alapján csökkent a steril neutrínó létezésének valószínűsége.

Fejlődési irányok

Annak érdekében, hogy választ kaphassunk a neutrínóoszcilláció legfontosabb nyitott kérdéseire, meg kell határozni a neutrínókeveredési mátrixban a θ₁₃ keveredési szög pontos értékét, a 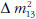tömegnégyzet-különbség előjelét és a neutrínókeveredés δ, φ₁, φ₂ fázisszögeit (a leptonoknál fellépő CP-invariancia esetleges sérülését). Ehhez nagyon intenzív neutrínónyalábok, erőteljes háttérlenyomás és nagy neutrínó repülési távolságok szükségesek. A CP-sérülés vizsgálatához a neutrínók és antineutrínók oszcillációjának összehasonlító analízisére is szükség van.

A nagy repülési távolságú neutrínókísérletekről az 1. táblázat ad áttekintést. A táblázat külön tárgyalja az első generációs szupernyaláb- és reaktorkísérleteket, valamint a második generációs szupernyaláb-, β-nyaláb- és a neutrínógyár-terveket.

Az első generációs szupernyaláb berendezések hagyományos módszerekkel főleg pionbomlásból eredő müonneutrínókat állítanak elő, de a protongyorsító teljesítménye nagyobb. A hagyományos módszerre példa a CERN-i berendezés a 6. ábrán. Ez viszonylag jól ismert technológia. A pionokat előállító protonnyaláb teljesítményét a második generációs szupernyaláboknál még tovább, 2–5 MW-ra kívánják növelni.

β-nyaláb berendezések. Vonzónak tűnik radioaktív β-bomló atommagok [például ⁶He (T_1/2 = 0,8 s, β^-) és ¹⁸Ne (T_1/2 = 1,7 s, β⁺)] gyorsítása ~150 GeV/nukleon energiáig, majd ezek tárolása tárológyűrűben. Így olyan elektronantineutrínó és -neutrínó nyalábokat nyerhetnénk, amelyek jól definiált ízzel rendelkeznek, energiaspektrumuk jól ismert és kollimáltságuk is kitűnő.

Neutrínógyárak. Nagy intenzitású neutrínóforrások előállítására müongyorsító építését is javasolták. Ebben nagy energiájú és intenzitású protonokkal nagy rendszámú céltárgyat bombáznak. Az elsődleges reakciótermékek zöme pion, amelyek gyorsan bomlanak müonokba. A müonok viszonylag hosszú ideig élnek (~2 µs), így fel lehet gyorsítani őket és tárolni egy olyan tárológyűrűben, amelyben hosszú egyenes szakasz van a detektor irányában. A tárolt például pozitív töltésű müonok 50%-ban elektronneutrínókat és 50%-ban müon-antineutrínókat szolgáltatnak, jól definiált energiaspektrummal.

A következőkben röviden ismertetjük az első és második generációs neutrínóberendezések főbb jellemzőit, amelyekről részletes információ található például Bandyopadhyay és mts. [9] munkájában. Ez egy nemzetközi munkacsoport vizsgálatának végeredményét tartalmazza.

Első generációs szupernyaláb kísérletek

A japán T2K (Tokai-to-Kamioka) kísérletben a J-PARC 30 GeV-es szinkrotronának nagy intenzitású protonnyalábját használják müonneutrínók előállítására. A neutrínók 295 km utat tesznek meg az 50 kilotonnás Szuper-Kamiokande föld alatti víz Cserenkov-detektorig. A T2K körülbelül két nagyságrenddel intenzívebb müonneutrínó "szupernyalábot" szolgáltat, mint a korábbi K2K. A müonneutrínó eltűnési vizsgálatokban pontosan meg akarják határozni a sin²(2θ₂₃) és 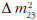értékeket. Vizsgálják továbbá a υ_µ → υ_e átalakulást, ami közvetve lehetőséget ad a θ₁₃ keveredési szög meghatározására is. 2010-ben már észlelték az első T2K neutrínók megjelenését a detektorban. A T2K kísérlet részletes leírása Wark [10] közleményében található.

Kísérletek reaktorneutrínókkal

A D-CHOOZ (Double-CHOOZ, Franciaország) programban két 4250 MW teljesítményű reaktorból származó elektron-antineutrínók eltűnését vizsgálják. A kísérlethez felhasznált két közepes méretű (0,011 kt) szcintillátor detektorból az egyik a reaktor mellett van, a másik ~1 km távolságban tőle. Három év alatt ~50 000, néhány MeV átlagenergiájú antineutrínót kívánnak detektálni.

A Daya Bay (Kína, Hong Kongtól 55 km-re északkeletre) program 3×2 reaktorra van alapozva, ami egyike a világviszonylatban legnagyobb teljesítményű nukleáris erőműkomplexeknek. Az antirészecskéket nyolc, lényegében azonos 20 kilotonnás szcintillációs detektorral regisztrálják föld alatti laboratóriumokban. A detektorok egyik része közeli (≤ 0,5 km), másik része távoli (2 km) telepítésű. A kísérlet elsőrendű célja a θ₁₃ keveredési szög meghatározása az eddigieknél nagyságrendileg jobb érzékenységgel. Ez megnyithatja az utat a későbbi leptonikus CP-invarianciasértési vizsgálatokhoz.

A Daya Bay kísérlet eltűnési kísérlet. A közeli detektorok a reaktorok -fluxusát mérik, a távoli detektorok a várt fluxustól való eltérést. A detektorok mélyen a hegy alatt vannak, így a kozmikus sugárzás okozta háttér kicsi. A detektorokat vízzel töltött tartály veszi körül, ami lehetőséget ad a környező sziklákból eredő radioaktivitás kiszűrésére. Két-három éves mérésidő után remélhetőleg elérnek 10^-1 érzékenységet a sin²2θ₁₃ meghatározásában (90%-os konfidenciahatárral). A legközelebbi detektorrendszer már működik, a távoli 2012-ben kezdi meg működését.

A jövőbeli neutrínóoszcillációs vizsgálatok egyik leglényegesebb eleme a jelenleg kevéssé ismert θ₁₃ keveredési szög és a Dirac- (δ), illetve Majorana- (φ₁, φ₂) fázisok meghatározása. A 7. ábra a sin²2θ₁₃ értékekre várható érzékenységi határokat mutatja az idő függvényében különböző neutrínókísérletekre. A (2) mátrix mutatja, hogy a δ hatása a neutrínókeveredésre szorosan összefügg a θ₁₃ értékével.

Második generációs szupernyaláb-tervek

A T2HK kísérlet a T2K továbbfejlesztett változata. A J-PARC-ban a protonnyaláb energiáját 50 GeV-re, teljesítményét 4 MW-ra kívánják növelni. Ez a Hiper-Kamikande-detektorral (ami 0,45 – 1 megatonnás víz Cserenkov-detektor lesz) elegendő eseményt fog szolgáltatni ahhoz, hogy versenyképes legyen a β-nyaláb vagy neutrínógyár berendezésekkel. Vizsgálják annak a lehetőségét is, hogy a J-PARC neutrínókat Dél-Koreában is detektálják víz Cserenkov-detektorral, ami a repülési távolságot L = 1000 km-re növelné. A υ_µ → υ_e,µ vizsgálatok tervbe vett ideje ~2 év, míg az antineutrínókra 8 év.

SNuMI-OA, NOυA. A Chicago melletti Fermi-laboratórium MINOS (Main Injector Neutrino Oscillation Search) programjának első változatában υ_µ-neutrínókat lőttek át a 725 km-re lévő Soudan (Minnesota) föld alatti laboratóriumba. A NOυA kísérletben a υ_µ → υ_e oszcillációban elérhető érzékenységet tízszeresen javítani akarják a MINOS első mérésekhez képest. Az SNuMI-OA változat 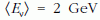átlagos neutrínóenergiát adna.

A Fermi-laboratórium Project-X tervében egy multimegawattos folytonos nyalábú protongyorsító létrehozása szerepel, ami rendkívül intenzív müonneutrínó-nyaláb létrehozását tenné lehetővé. A neutrínókat Dél-Dakotában lévő detektorhoz kívánják küldeni L ≈ 1300 km távolságba (CERN Courier, 2011. október, 54. o.). A nagy repülési távolság lehetővé teszi a abszolút értékének meghatározását.

BNL. A Brookhaveni Nemzeti Laboratóriumban lévő változó gradiensű szinkrotron 28 GeV-es protonnyalábjának teljesítményét 1 MW-ra kívánják növelni. A berendezéssel 0–6 GeV energiatartományban lévő neutrínókat lehetne előállítani, amiket a 2540 km-re lévő Homstake (Dél Dakota) bányában kívánnak regisztrálni 500 kilotonnás víz Cserenkov-detektorral. A υ_µ → υ_e,µ vizsgálatok tervezett mérésideje ~5-5 év neutrínókra és antineutrínókra. A berendezéssel például CP-sértő hatást lehetne tanulmányozni kisebb neutrínóenergiáknál.

CERN SPL. A CERN-ben tervbe vették egy szupravezető proton lineáris gyorsító (superconducting proton l inac, SPL) építését, ami >2,2 GeV-re gyorsítana protonokat 4 MW teljesítménnyel. A fejlesztés célja a CERN nagyenergiájú gyorsítóinál (protonszinkrotron, szuper protonszinkrotron, nagy hadronütköztető) a paraméterek javítása, valamint az eddigieknél kedvezőbb körülmények között radioaktív ionnyalábok és neutrínók előállítása. A berendezéssel hagyományos módon intenzív müonneutrínó és müon-antineutrínó nyalábokat lehetne előállítani. A neutrínókat ~400 kt tömegű víz Cserenkov-detektorral tervezik detektálni 130 km-re a CERN-től a Fréjus Modane-laboratóriumban. Az elérhető müonneutrínófluxus ~3,6 · 10¹¹ év^-1m^-2 lenne. Az újabb fejlemények azt mutatják, hogy ha az SPL protonok energiáját 3,5 GeV-re lehetne növelni, több másodlagos π/K mezont nyernének és ezek fókuszálásán is lehetne még javítani. Így összességében a neutrínófluxust ~3-szorosára lehetne növelni a 2,2 GeV-es konfigurációhoz képest. A mérésidő ~2 év lenne neutrínókra és nyolc év antineutrínókra.

β-nyaláb

Neutrínónyalábok előállítására egyik lehetőség radioaktív β- (és neutrínó-) bomlást mutató atommagok gyorsítása, majd tárolása tárológyűrűben (8. ábra). Így tiszta υ_e vagy 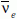nyalábok nyerhetők, amelyek energiaspektruma ismert és kollimáltságuk is kitűnő. A berendezéssel υ_e → υ_e eltűnési és υ_e → υ_µ, υ_e → υ_τ megjelenési neutrínó-ízváltozásokat lehetne vizsgálni, valamint hasonlókat elektron-antineutrínókkal.

A kísérlet legfontosabb sajátságait főleg három tényező befolyásolja.

• A gyorsított ion típusa és a β-bomlás energiája (E₀).
• A relativisztikus teljes energia per nyugalmi energia, a Lorentz-faktor (γ).
• A neutrínók repülési távolsága (L).

A gyorsított izotópnak elég hosszú ideig kell élnie, hogy a gyorsító fázisban le ne bomoljon, ugyanakkor – nagy neutrínófluxus elérése érdekében – ne legyen túl nagy az élettartama sem. Másodperc rendű élettartamok ésszerű kompromisszumnak látszanak. Több izotóp vizsgálata is számításba jöhet:

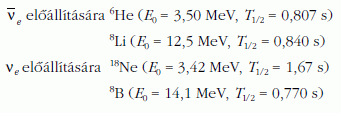
Ugyanolyan γ/L értéknél a neutrínónyalábok 3-4-szer nagyobb energiájúak Li/B ionoknál, mint He/Ne esetén. A részletes analízis azt mutatja, hogy kívánatos minél nagyobb γ-faktor elérése. Aszerint, hogy a berendezést hol valósítják meg, a következő γ-értékeket lehetne elérni a jelenleg létező infrastruktúrákkal:

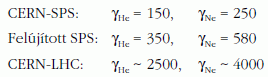
A neutrínók detektálására föld alatti laboratórium kívánatos a kozmikus sugárzás által keltett háttér csökkentésére.

Ha a β-nyaláb berendezést a CERN-ben hoznák létre és a ⁶He és ¹⁸Ne neutrínókat Fréjusban detektálnák (L = 130 km) 440 kilotonnás víz Cserenkov-detektorral, γ = 100 értéknél a szükséges mérésidő ~5 év lenne.

Az évenkénti töltött áramú események száma kilotonnás detektorban 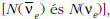, valamint az átlagos neutrínóenergiák 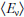a következőképpen alakulnak különböző ionokra, γ és L értékekre (oszcilláció nélküli esetre):

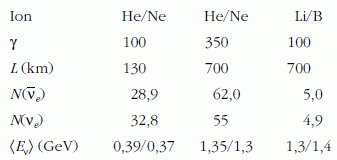
A β-bomló izotópok gyorsításával elérhető neutrínónyalábok lehetőségeit részletesen vizsgálja Lindroos, Mezetto [11] könyve, valamint Bandyopadhyay és mts. [9] és Gonzalez-Garcia, Maltoni [1] összefoglaló munkái.

Neutrínógyár

A neutrínógyár működési elve a következő (9. ábra). Egy nagy intezitású 5 < Ep<, 10 GeV energiájú protonnyalábot nagy rendszámú céltárgyra (például Hg-sugárra) ejtenek, ami nagyszámú piont kelt. A töltött pionokat kiválasztják a reakciótermékekből és fókuszálják. A töltött pionok közepes élettartama 2,60 · 10^-8 s, amelyek 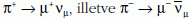bomlással bomlanak közel 100%-ban. A töltött müonok közepes élettartama 2,197 · 10^-6 s. Ez elegendően hosszú idő arra, hogy a müonokat néhányszor 10 GeV energiára lehessen gyorsítani. A gyorsított müonokat olyan tárológyűrűbe vezetik, amelyben a távoli detektor irányába mutató hosszú egyenes szakasz van. A müonok 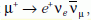, illetve 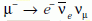bomlással bomlanak, így például a µ⁺ nyalábból 50%-ban υ_e, 50%-ban 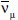neutrínók lépnek µ ki. A neutrínók energiaspektruma és fluxusa jól ismert. A neutrínógyár segítségével a következő oszcillációs folyamatok tanulmányozhatók:

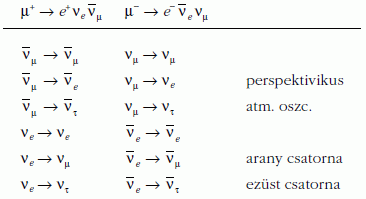
Ha nincs oszcilláció a ?e töltött áramú kölcsönhatása e^--t, míg a 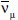töltött áramú kölcsönhatása µ⁺-ot hoz létre a detektorban, azaz az előállt lepton töltése nyomon követi a kezdeti neutrínó vagy antineutrínó ízét. Ha υ_e → υ_µ oszcilláció van, a υ_µ töltött áramú kölcsönhatása negatív müonokat kelt (azaz ellenkező előjelű müonokat). Ez nagyon tiszta kísérleti jelet ad az oszcillációra, ha szegmentált mágnesezett vas szcintillátor kalorimétert alkalmaznak a detektálásra, ami érzékeny az előállt lepton töltésére.

A neutrínógyárral elérhető neutrínódetektálási hozamokra a 2. táblázat ad információt, a tárolt müonok energiája (Eυ), valamint a neutrínók repülési távolsága (L) függvényében, 50 kilotonnás detektorra vonatkozóan. Különösen figyelemre méltó, hogy még 7300 km forrás-detektor távnál is a várható események száma elegendő ahhoz, hogy a neutrínók ízváltozási valószínűségét nagy érzékenységgel lehessen mérni.

A protonnyaláb és céltárgy megválasztásánál a következő szempontokat célszerű érvényesíteni (Geer [12]):

• A proton energiáját célszerű 5 < E_p< 10 GeV között megválasztani, hogy a töltött pionok hozama maximális legyen rögzített nyalábteljesítménynél.
• A csomósított protonnyaláb hossza < 3 ns legyen, ami a további gyorsítási fokozatok miatt szükséges.
• A szükséges nyalábteljesítmény 4 MW, ami remélhetőleg elérhető.
• Céltárgynak célszerű folyékony Hg-nyalábot használni. Egy 20 T-s szolenoiddal radiálisan össze lehet nyomni minden céltárgyból kilépő töltött piont.

Bandyopadhyay és mts. [9] (International Scoping Study, ISS) összehasonlító analízist végeztek különböző másodgenerációs neutrínóberendezések képességeire vonatkozóan. Elsősorban a θ₁₃ keveredési szög, a neutrínó tömeghierarchia és a δ_CP neutrínókeveredési fázis meghatározására koncentráltak. Az összehasonlításokat konzervatív és optimalizált paraméterek mellett végezték, amelyek a következők:

konzervatív paraméterek

• 50 GeV-es tárolt müonnyaláb
• 10²¹ hasznos müonbomlás évenként
• a kísérleti idő 4 év pozitív töltésű müonokra és 4 év negatív töltésűekre
• a detektor 50 kilotonnás szegmentált vas szcintillátor kaloriméter, MINOS típusú
• a neutrínó repülési hossza 4000 km

optimalizált paraméterek

• 20 GeV-es tárolt müonnyaláb
• 10²¹ hasznos müonbomlás évenként
• a kísérlet ideje 5 év a pozitív töltésű és 5 év a negatív töltésű müonokra
• a detektor: 50 kilotonnás, MINOS típusú, de továbbfejlesztett
• A neutrínók repülési hossza 4000 és 7500 km

A sin²2θ₁₃-ra vonatkozó felfedezési esélyek a különböző másodgenerációs neutrínóberendezésekre a 10. ábrán láthatók. Összehasonlításul: a jelenlegi kísérleti határ a sin²2θ₁₃-ra 10^-1, míg a reaktor és hagyományos nyaláb kísérletekből 10^-2 várható. A szupernyalábokkal ~10^-3, a neutrínógyárral 10^-5 rendű kísérleti határ lesz elérhető.

Bandyopadhyay és mts. [9] közleményében az 10. ábrához hasonló ábrák láthatók a neutrínótömeghierarchia és a δ CP-megmaradást sértő fázis felfedezési lehetőségeire vonatkozóan is. Összefoglalóan az várható, hogy legjobb esélye mindhárom mennyiség meghatározására a neutrínógyárnak van. Második helyen a T2HK kísérlet áll (a θ₁₃ és tömeghierarchia meghatározására), valamint a β-nyaláb (a CP-sértő fázisnál). Annak lehetőségét, hogy a CP-megmaradás sérülését észleljék – a lepton szektorban Majorana-fázisokon keresztül – sokan vizsgálták és reményteljesnek tartják (lásd [9]-ben).

Megjegyzendő, hogy hamis következtetések elkerülése érdekében sokféle információt kell begyűjteni a neutrínógyár-kísérleteknél. Célszerű a méréseket mind pozitív töltésű, mind negatív töltésű müonokkal elvégezni, és mérni kell a hozamokat és neutrínó-energiaspektrumokat is, lehetőleg minél több eltűnési és megjelenési neutrínóoszcillációra vonatkozóan (összesen 12-féle lehet).

A neutrínógyár létesítése mellett szól továbbá az is, hogy a müon-tárológyűrű egyúttal lehetőséget ad sokféle müonfizikai mérés elvégzésére. Az új (kisenergiájú) müonforrás intenzitása 3-4 nagyságrenddel nagyobb lenne, mint a jelenleg elérhetőké. Ez lehetőséget adna nagyon ritka, a müoncsaládszám megmaradását sértő folyamatok vizsgálatára (például µ⁺ → e⁺ γ, µ⁺ → e+ e^- e⁺), valamint a müon esetleges elektromos dipólnyomatékának mérésére. A neutrínóoszcilláció felfedezése óta valószínű, hogy a leptoncsaládszám megmaradása sérül. A jelenlegi kísérleti felső határ a µ → e γ folyamatra 10^-11 rendű. A leptoncsaládszám megmaradásának sérülése töltött lepton folyamatokban annak függvénye, hogy a neutrínótömeget milyen folyamat generálja. A leptoncsaládszám sérülése nagy lehet, ha új részecskék vagy kölcsönhatások léteznek a ≥TeV-es tartományban. Így e vizsgálatok a neutrínótömeg eredetére is fontos információt szolgáltathatnak.

A neutrínófizikai vizsgálatokat a háttérsugárzás csökkentése érdekében célszerű föld alatti laboratóriumokban végezni. A mélyen föld alatti laboratóriumokról, bennük a neutrínófizikai és kettős β-bomlási vizsgálatokról Spooner [13] közölt összefoglalót.

Összefoglalás

A neutrínófizika az 1930-as évektől kezdve hatalmas fejlődésen ment keresztül. Egyik legutóbbi, áttörő felfedezése a neutrínóoszcilláció volt, ami az első kísérleti alapon nyugvó bizonyítéka a Standard modellen túlmutató fizikának. A jelenleg folyó első generációs szupernyaláb- és reaktorneutrínós kísérletek, továbbá a neutrínógyár-tervek reális lehetőséget nyújtanak a neutrínókeveredés még gyakorlatilag ismeretlen paramétereinek (θ₁₃, δ_CP, …) meghatározására. Ez elősegítheti a leptogenezis megértését és hozzájárulhat egészen alapvető fontosságú rejtélyek megfejtéséhez; például hogy az ismert Világegyetemünk miért lényegében csak anyagból (és nem antianyagból) áll, vagy hogy miért olyan kicsi a neutrínók tömege a töltött leptonok tömegéhez képest [2].

Irodalom

1. M. C. Gonzalez-Garcia, M. Maltoni: Phenomenology with massive neutrinos. Phys. Rep. 460 (2008) 1.
2. R. N. Mohapatra et al.: Theory of neutrinos: a white paper. Rep. Prog. Phys. 70 (2007) 1757.
3. Particle Data Group, Review of particle physics, Phys. Lett. 667 (2008) 1.
4. Particle Data Group, Review of particle physics, J. Phys. G 37 (2010) 075 021.
5. T. Fényes: Részecskék és kölcsönhatásaik. 2. korszerűsített kiadás, Debreceni Egyetemi Kiadó, 2012. Közlés alatt.
6. T. Araki et al., Phys. Rev. Lett. 94 (2005) 081 801.
7. J. Lesgourgues, S. Pastor, Phys. Rep. 429 (2006) 307.
8. K. Elsener, Ch. Sutton, CERN Courier (2004/October) 27.
9. A. Bandyopadhyay et al.: Physics at a future neutrino factory and super-beam facility. Rep. Prog. Phys. 72 (2009) 106 201.
10. D. Wark: The T2K experiment. Nucl. Phys. News 19/4 (2009) 26.
11. M. Lindroos, M. Mezzetto: Beta beams: neutrino beams. Imperial College Press; Annu. Rev. Nucl. Part. Sci. 60 (2010) 299.
12. S. Geer: Muon colliders and neutrino factories. Annu. Rev. Nucl. Part. Sci. 59 (2009) 347.
13. N. Spooner, Nucl. Phys. News 18/4 (2008) 13.