
Fizikai Szemle honlap |
Tartalomjegyzék |
Pákó Gyula
ELTE Apáczai Csere János Gyakorlógimnázium
A 2011. évi Eötvös-versenyt október 14-én rendezték meg, az ünnepélyes eredményhirdetésre november 25-én 15 órakor került sor az ELTE TTK Lóczy Lajos termében.
A megjelenteket Radnai Gyula, a versenybizottság elnöke köszöntötte. Az ünnepség első részében az utóbbi évek hagyományának megfelelően kivetítette és felolvasta az 50, illetve 25 évvel ezelőtti feladatokat, ismertette a versenyek helyezettjeit, akiket igyekezett felkutatni és meghívni, végül bemutatta a jelenlévő egykori díjazottakat.

1. feladat
1 m hosszú, 0,25 g/cm3 sűrűségű vékony fapálcát
víz felszíne felett lógatunk úgy, hogy alsó vége 2 m-re
van a víz színe felett. A pálcát elengedjük.
Vízbe esve milyen mélyre süllyed le a pálca a vízben? Mi történik, ha a pálcát 0,5 m magasról ejtjük le? Mi történik, ha a pálcát a víz színe alól indítjuk el úgy, hogy felső vége indításkor 10 cm-re van a víz szintje alatt? Mi történik, ha ezt 0,75 g/cm3 sűrűségű pálcával tesszük meg?
Minden súrlódás és közegellenállás elhanyagolandó.
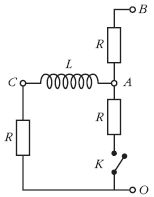
2. feladat (Károlyházy Frigyes)
Kapcsolásunkban a föld és B
pont közé hosszabb idő óta 300
V egyenfeszültség van kapcsolva.
Az R ellenállások mindegyike
100 ω-os és az L tekercs önindukciója
10 H. A K kapcsolót
hirtelen kikapcsoljuk.
Mennyivel ugrik az A pont feszültsége közvetlenül a kapcsoló megszakítása után (például ezredmásodpercen belül)?
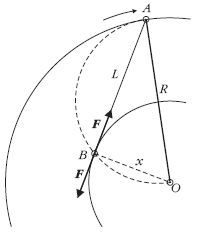 3. feladat (Károlyházy Frigyes)
3. feladat (Károlyházy Frigyes)
Ostornyél egyik végére vékony cérnaszálon elenyésző
tömegű tollpihét kötünk, és körbe forgatjuk.
Milyen pályán mozog a pihe?
A megoldásokat és a díjazottak névsorát a Versenybizottság akkori elnöke, Vermes Miklós ismertette a Középiskolai Matematikai Lapok 1962. évi 1-2. számában.
Radnai tanár úr bemutatta a 3. feladat Vermes Miklós által közölt tömör, ötletes megoldását.
A pihére jellemző, hogy nincs tömege, súlya, és csak a közegellenállási erő hat rá. Az R = AO hosszúságú pálca végére L = AB hosszúságú fonálra kötött pihére az F közegellenállási erő a sebesség irányával ellentétesen hat, tehát a A fonál iránya a pihe pályakörének érintője. A bot vége R = AO sugarú kört ír le. A pihe pályakörének x sugarát Thalész-körrel kapjuk meg: x = (R2-L2)1/2. Ha a cérna hosszabb, mint a pálca, akkor nincs stabil pálya.
Az 50 évvel ezelőtti verseny I. helyezettje Zakariás László a budapesti Piarista Gimnázium tanulója, tanára Kovács Mihály. II. díjat kapott Fritz József a mosonmagyaróvári Kossuth Lajos Gimnázium tanulója, tanára Németh Béláné. Dicséretben négyen részesültek: Bollobás Béla a budapesti Apáczai Csere János Gyakorlógimnáziumban Csernák Emil tanítványa, Molnár Emil a győri Révai Gimnáziumban Bőnyi Mihály tanítványa, Perjés Zoltán a budapesti Piarista Gimnáziumban Kovács Mihály tanítványa és Sólyom István a budapesti Vörösmarty Gimnáziumban Óhegyi Ernő tanítványa.
Az 1961. évi verseny díjazottjai közül jelen volt Zakariás László, Fritz József és Molnár Emil.

Elsőként Zakariás László olvasta fel visszaemlékezését. Gondosan megfogalmazott mondatokban hálával és szeretettel emlékezett meg volt iskolájáról a budapesti Piarista Gimnáziumról, Kovács Mihály tanár úrról, aki nemcsak fizikatanára, hanem osztályfőnöke is volt.
"… Az első hónapok nagyon keservesen teltek: egyre-másra vittem haza a rossz jegyeket. Az, hogy nem hagytam ott akkor az iskolát, és négy év múlva kitűnően érettségiztem, majd részt vettem az Eötvös-versenyen, jórészt Kovács tanár úrnak köszönhető. Az útmutatása egyszerű volt: »Fiam, dolgozni kell. Az eredmények majd megjönnek.« Hát dolgoztam. És a jegyeim egyre jobbak lettek. Hozzászoktunk a követelményekhez. Az iskola nem szigorú volt, hanem igényes. Ez az igényesség - lassan-lassan - számunkra is természetessé vált.…
A kedvenc tantárgyam természetesen a fizika volt. Kovács tanár úr minden eszköz nélkül is nagyon szemléletesen tudott magyarázni. Kezével a levegőbe rajzolta a kísérletet: »Én már látom, már a vak is látja, no ki látja még?« És láttuk. Értettük. Persze ennek ellenére, mindig sokat dolgozott azon, hogy érdekes kísérletekkel támassza alá a magyarázatát. Ha kellett, maga készített eszközöket a szemléltetéshez. …
Gondolkodását a lényeglátás jellemezte. Minket is erre nevelt. Megkülönböztetni a probléma szempontjából fontos és lényegtelen dolgokat, az utóbbiakkal nem foglalkozni: ezek csak elvonják a figyelmet a lényeges összefüggések fölismerésétől. …
A műszaki egyetemre első próbálkozásra nem vettek föl. Ősszel kihirdették az Eötvös-verseny eredményét. Első díjat nyert Zakariás László, az Elektronikus Mérőkészülékek Gyárának dolgozója. »Te miért nem akarsz egyetemre menni?« kérdezte egy társam. Csak mosolyogtam. A műszaki egyetemre második próbálkozásra sem vettek föl. Fellebbeztünk. A fellebbezést elutasították. A minisztériumi fellebbezéshez csatoltuk az Eötvös-verseny eredményét. Szeptember végén, a születésnapomon, levél érkezett a minisztériumból. Örömmel értesítjük, hogy felvételt nyert a Budapesti Műszaki Egyetem Villamosmérnöki Karára. Én voltam a világ legboldogabb embere.”
Fritz József jelenleg a Budapesti Műszaki Egyetem Differenciálegyenletek Tanszékének egyetemi tanára, akadémikus. Visszaemlékezésében elmondta, hogy a középiskolában kezdetben a matematika iránt érdeklődött, de főleg tanárának köszönhetően IV. osztályos korára megszerette a fizikát. Egyetemi tanulmányait az ELTE TTK fizikus szakán kezdte, majd két tanév után matematikusként folytatta. Úgy gondolta ugyanis, hogy a fizika megértéséhez a matematikán keresztül vezet az út. Jelenleg a hidrodinamika mikroszkopikus elméletével foglalkozik, ami akár a fizika fejezete is lehetne. Ebből kiindulva a továbbiakban a fizika és a matematika kapcsolatáról beszélt Galileitől napjainkig.
Molnár Emil matematika-fizika-ábrázoló geometria szakot végzett, ma a Budapesti Műszaki Egyetem Geometria Tanszékének professzora. Ő is megemlékezett egykori tanárairól. Matematikára édesapja tanította, fizikatanára Bőnyi Mihály volt, de nagyon sokat köszönhet a Középiskolai Matematikai Lapok akkoriban indult fizika pontversenyének is. Központilag szervezett szakkörük meghívott előadói voltak többek között Vermes Miklós és Abonyi Iván. A verseny második feladatát nem tudta megoldani, a harmadikra viszont Vermes tanár úréval egyenértékű megoldást adott.
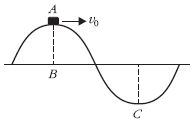 1. feladat (Vermes Miklós)
1. feladat (Vermes Miklós)
Egy 15 kg tömegű test A
súrlódásmentesen csúszik v0
végig egy szinusz alakú
lejtőn. Amikor A-ban van,
akkor sebessége v0 = 6
m/s, és ekkor éppen nem
nyomja a lejtőt.
Mekkora erővel nyomja a lejtőt, amikor C-ben van? AB = 1,4 m, g = 10 m/s2.
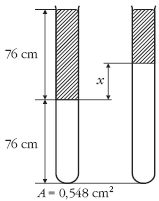 2. feladat (Szegedi Ervin)
2. feladat (Szegedi Ervin)
Egy A = 0,548 cm2 keresztmetszet területű, alul zárt,
felül nyitott, 152 cm hosszú cső alsó felében 304 K
hőmérsékletű levegő, felette
higany van. Az elzárt levegő
hőmérsékletét lassan emeljük.
A külső levegő nyomása 76 cm magas higanyoszlop nyomásával tart egyensúlyt. Ezen a nyomáson, 304 K hőmérsékleten a levegő sűrűsége 1,2 g/dm3. A levegő fajhője állandó térfogaton cv = 0,75 J/gK. A higany és az üveg hőtágulásától eltekintünk.
 3. feladat (Vermes Miklós)
3. feladat (Vermes Miklós)Mekkora a kondenzátor kapacitása?
A megoldásokat és a díjazottak névsorát Vermes Miklós ismertette a Középiskolai Matematikai Lapok 1987. évi 2. számában.
Az 1986. évi versenyen I. díjat ketten kaptak egyenlő helyezésben, Kaiser András és Kohári Zsolt. Mindketten a Budapesti Műszaki Egyetem Villamosmérnöki Karának hallgatói, a budapesti Fazekas Mihály Gyakorló Gimnáziumban érettségiztek, mint Horváth Gábor tanítványai.
II. díjat kapott Drasny Gábor, a budapesti Fazekas Mihály Gyakorló Gimnázium III. osztályos tanulója, tanára Horváth Gábor.
III. díjat öten kaptak. Jakovác Antal honvéd, aki a budapesti Apáczai Csere János Gyakorlógimnáziumban érettségizett, mint Kelemen László tanítványa. Ligeti Zoltán és Montágh Balázs, az Eötvös Loránd Tudományegyetem Természettudományi Karának fizikus, illetve matematikus hallgatói, mindketten a budapesti Fazekas Mihály Gyakorló Gimnáziumban érettségiztek, mint Horváth Gábor tanítványai. Cynolter Gábor és Gyuris Viktor, a budapesti Fazekas Mihály Gyakorló Gimnázium IV. osztályos tanulói, tanáruk Horváth Gábor.
Dicséretet ketten kaptak egyenlő helyezésben. Benczúr András a budapesti Fazekas Mihály Gyakorló Gimnázium IV. osztályos tanulója, tanára Horváth Gábor; és Török Balázs a budapesti I. István Gimnázium végzős tanulója, tanára Moór Ágnes.
A bizottság dicsérőleg állapította meg, hogy a 2. feladatra kiemelkedően szép megoldást adott Majoros László, a budapesti Fazekas Mihály Gyakorló Gimnázium IV. osztályos tanulója, tanára Horváth Gábor.
Radnai tanár úr a KöMaL arcképcsarnokából kigyűjtötte és kivetítette a díjazottak egykori fényképeit.
A 25 évvel ezelőtti verseny mindkét I. helyezettje megjelent.
Kohári Zsolt gimnáziumi fizikatanára, a teremben is jelenlévő Horváth Gábor szerepét emelte ki abban, hogy sikeres lehetett az Eötvös-versenyen. A Budapesti Műszaki Egyetem Villamosmérnöki Karán végzett, ma ott oktató, informatikát tanít. Reméli, hogy abból a szemléletből, amit volt tanáraitól kapott, oktatóként minél többet sikerül továbbadnia.
Kaiser András köszönetet mondott egykori tanárainak és osztálytársainak, akiknek jelentős szerepük volt az eredmények elérésében. További sikereket kívánt a mai diákoknak, illetve arra kérte őket, hogy fordítsanak figyelmet a politika, a gazdaság és a pénzügyek világára is, mert az országnak jelenlegi helyzetében szüksége van jól felkészült, függetlenül gondolkozó, okos emberekre.

Drasny Gábor az ELTE TTK matematikus szakán végzett, tizenkét éve él az Amerikai Egyesült Államokban, az IBM-nél chipek tervezését és ellenőrzését segítő szoftvereket tervez. Ő levélben köszöntötte a versenyzőket. "Nagy volt az örömöm, amikor kiderült, hogy második díjat kaptam. Tovább növelte a boldogságot, hogy a tíz díjazottból 8 iskolatársam volt, sőt mindnyájan Horváth Gábor tanár úr tanítványai voltunk, akinek sokat köszönhetünk. Azt hiszem, ennek a 25 évvel ezelőtti versenynek az igazi nyertese ő volt.”
A szintén Amerikában tartózkodó Gyuris Viktor is levélben szólt a versenyzőkhöz. "Huszonöt éve magam is közöttetek ültem. A fizika és a matematika töltötte ki az iskolai és szabadidőm nagy részét. Tanáraimtól - Horváth Gábortól, Honyek Gyulától és Gnädig Pétertől (ismerősek a nevek?) olyan lelkesedést kaptam, ami teljesen magával ragadott. A tárgy oly végtelen egyszerűnek tűnt. Oly átlátható és tiszta….” Ma ő is szoftverkészítéssel foglalkozik.

A leveleket Honyek Gyula és Vigh Máté, a Versenybizottság tagjai olvasták fel.
Cynolter Gábor elméleti fizikusként az ELTE-n dolgozik, azokban a napokban egy szemináriumon Bécsben tartózkodott.
Az 50, illetve a 25 évvel korábbi versenyek felidézése után az ünnepség rendhagyó módon, az I. díj átadásával folytatódott. Radnai tanár úr köszöntötte Kroó Norbertet, az Eötvös Loránd Fizikai Társulat elnökét és megkérte, hogy adja át az I. díjat. Mielőtt ez megtörtént volna, Kroó Norbert röviden szólt a megjelentekhez.
"Miközben hallottam a dicsérő mondatokat, egy olyan mondás jutott eszembe, amely most mind a tanárkollégáknak, mind a fiataloknak szól. Annak idején Newton a következőt mondta: ha netán az történt, hogy én messzebbre láttam, mint a kortársaim, az azért volt, mert óriások vállán állhattam. Azok a sikerek, amelyeket a fiatal kollégák példamegoldásban elértek azt jelentik, hogy szerencsére Magyarországon is vannak még óriások. Ezt különösen akkor fontos hangsúlyozni, ha azt látjuk, hogy például a Debreceni Egyetemre ketten jelentkeztek fizikatanárnak. Tudjuk, hogy százas nagyságrendű fizikatanár vonul nyugdíjba évente. Vészharangot kell kongatni, és a vészharang akkor szól a leghangosabban, ha azt egyre többen kongatják."
A fiatalokhoz szólva idézte kedvenc tanárát. "Ha nagyon pontosan tudod, hogy mit akarsz, és azt elég erősen akarod, akkor azt el is fogod érni. Ez persze nem megy magától. Senki se felejtse el, hogy munka nélkül nincs eredmény."
A körülmények ma zavarosabbak, mint korábban voltak, ebben helyesen tájékozódni legalább olyan fontos, mint fizikafeladatokat jól megoldani. A továbbiakra mindenkinek sok sikert és örömöt kívánt.
Kroó professzor mellett Csernik Kornél a MOL képviseletében és Kürti Jenő, Társulatunk főtitkára adta át a díjat.
A 2011. évi verseny I. helyezettje Budai Ádám a Budapesti Műszaki Egyetem BSc hallgatója, aki a miskolci Földes Ferenc Gimnáziumban érettségizett, mint Bíró István és Zámborszky Ferenc tanítványa.
Radnai tanár úr bejelentette, hogy az első helyezett 30 000 Ft pénzjutalomban is részesül. A MOL által nyújtott támogatásból a díjazott versenyzők tanárai 20 000 Ft-os kedvezménnyel vehetnek részt a 2012. évi fizikatanári ankéton. A jelenlévő tanárok továbbá választhatnak a kiállított könyvekből, melyek a Typotex és a Vince Kiadó adományai.
Kroó Norbert köszönetet mondott a MOL nagyvonalú anyagi támogatásáért.
A továbbiakban a szokásos módon folytatódott a rendezvény. Radnai tanár úr egyesével haladva kivetítette és felolvasta a feladatokat, majd részletesen ismertette a megoldásokat. A harmadik feladat eredményeit kísérletben is megvizsgáltuk.
1. feladat
Pályafutásuk végén a sorsukra hagyott műholdak a
sebesség négyzetével arányos légellenállási erő hatására
fokozatosan veszítenek mechanikai energiájukból,
és végül a légkör sűrűbb rétegeibe érve elégnek.
Belátható, hogy az eredetileg körpályákon keringő
műholdak a Föld felszínéhez közeledve mindvégig
közelítőleg körpályákon haladnak, miközben a "körpályák"
sugara lassan csökken.
Tegyük fel, hogy egy m0 = 500 kg tömegű műholdat, amely az Egyenlítő síkjában, h = 400 km-es magasságban körpályán kering, magára hagynak! A műholdra ható légellenállási erőt az Flég = Kρ v2 alakban adhatjuk meg, ahol K = 0,23 m2, ρ a levegő sűrűsége a műhold magasságában, v pedig a műhold sebessége.
A megoldáshoz szükséges további adatokat táblázatokból vehetjük.
2. feladat
Egy függőlegesen álló, henger alakú zárt tartály
magassága legyen 20 cm! Tegyük fel, hogy a tartály
falának és belső tartalmának hőmérséklete huzamos
ideje T = 1 °C! A tartalom pedig egy, a tartály alaplapját
borító papírvékonyságú vízréteg és fölötte ennek a
telített gőze, más semmi. Az oldalfalat hőszigetelőnek
tekinthetjük, az alap- és fedőlap azonban igen jó hővezető
vékony fémlemez, amelyek hőmérsékletét
kívülről szabályozhatjuk.
A lehetőséggel élve emeljük a fedőlap hőmérsékletét Tf = 100 °C-ra, miközben az alaplap hőmérsékletét T = 1 °C-on tartjuk, és gondoskodjunk róla, hogy ezek az értékek elég sokáig így maradjanak! Várjuk meg, amíg az edényben kialakul a víz, illetve a gőz új stacionárius állapota, amely már nem változik tovább!
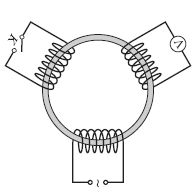 Egy toroid (úszógumi)
alakú "sovány" vasmagra
szimmetrikus elrendezésben
három egyforma
"kövér" elektromágneses
tekercs van felfűzve az
itt látható ábra szerint.
Az első tekercsre váltóáramú
feszültségforrást
kapcsolunk, a második
tekercs kivezetéseit szabadon hagyjuk, a harmadik
tekercs csatlakozóira pedig voltmérőt kötünk. Ekkor a
voltmérő a feszültségforrás effektív értékének felét
mutatja.
Egy toroid (úszógumi)
alakú "sovány" vasmagra
szimmetrikus elrendezésben
három egyforma
"kövér" elektromágneses
tekercs van felfűzve az
itt látható ábra szerint.
Az első tekercsre váltóáramú
feszültségforrást
kapcsolunk, a második
tekercs kivezetéseit szabadon hagyjuk, a harmadik
tekercs csatlakozóira pedig voltmérőt kötünk. Ekkor a
voltmérő a feszültségforrás effektív értékének felét
mutatja.
Ezután a második tekercs kivezetéseit a K kapcsolóval rövidre zárjuk. Mit mutat ebben az esetben a voltmérő?
Útmutatás: A tekercsek ohmos ellenállása elhanyagolható, a feszültségforrást és a voltmérőt ideálisnak tekinthetjük. A vasmag mágneses permeabilitása nem függ a mágneses fluxustól.

Az első feladathoz Honyek Gyula és Kürti Jenő fűzött megjegyzést. Honyek tanár úr utalt a feladat véletlen aktualitására, a NASA Felső Légköri Kutató Műholdjának (UARS) közelmúltbeli, Csendes-óceánba való lezuhanására.
A harmadik feladat egy lehetséges másik megoldását vázolta hozzászólásában Zakariás László.
A 2011. évi feladatsor megoldása várhatóan a Középiskolai Matematikai Lapok 2012. évi 3. számában jelenik meg.
A megoldások ismertetése után, a megkezdett sorrendben folytatódott az eredményhirdetés. A díjakat a továbbiakban Kürti Jenő és Csernik Kornél adta át.

II. helyezést hárman értek el: Jéhn Zoltán, a Budapesti Műszaki Egyetem fizika szakos BSc hallgatója, aki a pécsi Babits Mihály Gyakorlógimnáziumban érettségizett, mint Koncz Károly és Kotek László tanítványa.
Kalina Kende, az Eötvös Loránd Tudományegyetem Természettudományi Karának matematika szakos BSc hallgatója, aki a budapesti Fazekas Mihály Gyakorló Gimnáziumban érettségizett, tanárai voltak Horváth Gábor, Csefkó Zoltán és Szokolai Tibor.
Szabó Attila a pécsi Leőwey Klára Gimnázium 11. évfolyamos tanulója, felkészítő tanárai Simon Péter és Kotek László.
III. díjat ketten vehettek át: Bolgár Dániel a pécsi Leőwey Klára Gimnázium 12. évfolyamos tanulója, felkészítő tanárai Almási László és Simon Péter.
Kovács Péter az ELTE Apáczai Csere János Gyakorlógimnázium 12. évfolyamos tanulója, tanára Pákó Gyula.
Dicséretben hárman részesültek: Batki Bálint, a Budapesti Műszaki Egyetem fizika szakos BSc hallgatója, aki az ELTE Apáczai Csere János Gyakorlógimnáziumban érettségizett, mint Zsigri Ferenc tanítványa. Forman Ferenc, az ELTE Radnóti Miklós Gyakorlógimnázium 10. évfolyamos tanulója, felkészítő tanára Honyek Gyula. Jenei Márk, a budapesti Fazekas Mihály Gyakorló Gimnázium 11. évfolyamos tanulója, Dvorák Cecilia és Csefkó Zoltán tanítványa.
A II. és III. helyezést elért versenyzők pénzjutalomban, a dicséretet kapott tanulók könyvjutalomban részesültek, továbbá valamennyi díjazott átvehette a Nemzeti Tankönyvkiadó Ember a Holdon című kiadványát.
Az ünnepség végén Radnai tanár úr köszönetet mondott a támogatóknak és meghívta a résztvevőket az állófogadásra, amelynek anyagi hátterét a Ramasoft Zrt. biztosította. Elkészült a szokásos csoportkép is a 2011. évi verseny díjazottjairól.