A LORENTZ-INGA

Hraskó Péter
PTE Elméleti Fizika Tanszék

Lorentz kérdése az I. Solvay-konferencia résztvevőihez

1863-ban a 25 éves Ernst Solvay belga vegyész kidolgozta az ipari szódagyártás technológiáját és hatalmas vagyonra tett szert. De nem csak a szóda érdekelte. Lorentz szerint "Belgiumnak ez a legnemeslelkűbb állampolgára mélyen meg volt róla győződve, hogy a természet és a társadalom törvényszerűségeinek alaposabb megismerése az emberiség boldogulását segíti elő". Solvay jelentős összegeket áldozott a tudományra. Többek között pszichológiai, szociológiai, kémiai intézeteket alapított. 1911-ben W. H. Nernst javaslatára Brüsszelben összehívta az I. Nemzetközi Solvay-konferenciát, amelyen a kor legnevesebb 22 fizikusa (közöttük H. Poincaré, M. Planck, W. Wien, A. Sommerfeld, E. Rutherford, A. Einstein) vett részt, és a további Solvay-kongresszusok szervezését 1 millió frank alaptőkével létrehozott Nemzetközi Fizikai Intézetre bízta.

1911 arra az időszakra esett, amikor a fizika mélységes – de mint később kiderült, rendkívül termékeny – válságban volt. Lorentz, a konferencia elnöke, bevezetőjében azt mondta, hogy "ma messze vagyunk a szellemi kielégültségnek attól az állapotától, amelyet a fizikai elmélet húsz, vagy akár csak tíz évvel ezelőtt nyújtani tudott. Nem szabadulhatunk attól a gondolattól, hogy zsákutcába kerültünk: a régi elméletek egyre kevésbé képesek eloszlatni a homályt, amely minden oldalról körülvesz." Majd így folytatta: "Planck esszéje az energiakvantumokról »valóságos fénysugár« ebben a ködben, és most az a feladat, hogy olyan mechanikát dolgozzunk ki, amelyből Planck felfedezése következményként adódik." Mint jól tudjuk, Planck úgy tudta megmagyarázni a fekete sugárzás spektrumát, ha feltételezte, hogy a harmonikus lineáris oszcillátor energiája csak a hν = ħω kvantum egész számú többszöröse lehet.¹

A lineáris harmonikus oszcillátor egyik legegyszerűbb példája a matematikai inga. Lorentznek ez szöget ütött a fejébe és a következő kérdéssel fordult a konferencia résztvevőihez: A matematikai inga körfrekvenciája

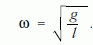
Planck szerint az energiája csak ħω egész számú többszöröse lehet, vagyis E = n ħω-val egyenlő n = 0, 1, 2… mellett. Mármost, ha az inga fonalát a két ujjunkkal összecsippentve az inga hosszát folyamatosan csökkentjük, akkor az ω körfrekvencia folyamatosan nő. Hogyan képzelhető el, hogy eközben az energiája állandóan ħ ω egész számú többszöröse marad?

Einstein, aki ismerte P. Ehrenfest idevágó munkáit, kapásból válaszolt Lorentz kérdésére: a mechanika törvényei szerint a hossz lassú növelésével vagy csökkentésével az energia úgy változik, hogy az E/ω hányados közben állandó maradjon; a folyamat során tehát Planck képlete folyamatosan érvényes lesz ugyanazzal az n értékkel. Lorentz ezekkel a szavakkal nyugtázta Einstein magyarázatát: "Ez a rendkívül meglepő eredmény megoldja az általam felvetett problémát. Általában is az energiakvantumok hipotézise érdekes kérdésekhez vezet minden olyan esetben, amikor a frekvencia önkényesen változtatható."

A konferencia jegyzőkönyve szerint senki sem vetette fel, mi van akkor, ha ω-t gyorsan változtatjuk: mindenkit lenyűgözött az a tény, hogy a klasszikus mechanika a lassú változás esetében ilyen csodálatos harmóniában van az energiakvantum-hipotézissel.

Mai ismereteink fényében Einstein válasza a kvantummechanika ma is érvényes fontos tételének első megfogalmazása: amikor egy fizikai rendszer határozott kvantumállapotban van és közben lassan változtatjuk egy vagy több paraméterét, a rendszer folyamatosan megmarad az ugyanazokkal a kvantumszámokkal jellemzett állapotában. Ha a paraméterek az eredeti értékükre állnak vissza, a rendszer is visszakerül eredeti állapotába: a körfolyamat során nincs munkavégzés.

Amikor azonban a változás gyors, a rendszer közben gerjed. Ha például eredetileg alapállapotban volt, akkor hiába állítjuk vissza a paraméterek korábbi értékét, bizonyos valószínűséggel gerjesztett állapotban marad vissza.

Az E/ω állandóságának igazolása

Az E/ω állandóságának igazolásához azt kell megmutatnunk, hogy ezen arány időderiváltja nullával egyenlő. Az olyan mechanikai rendszerek esetében, amelyek E energiája a K kinetikus és az U potenciális energia összegével egyenlő, és csak U tartalmazza a változó paramétert, az E időderiváltja az

képlet alapján számítható ki. A bal oldalon teljes derivált áll, mert számításba kell venni minden okot – a koordináták és a sebességek megváltozását csakúgy, mint a külső körülményekét – ami az energia értékét megváltoztathatja. A teljes időderiváltat a szokásoknak megfelelően gyakran fogjuk ponttal jelölni. A jobb oldalon a parciális időderivált jelzi, hogy itt csak az explicit időfüggés (vagyis a körülmények időbeli változása) veendő figyelembe. Az (1) magában foglalja az energiamegmaradás tételét, amely azt mondja ki, hogy amikor a körülmények időben állandók, a rendszer energiája nem változik.

Egy szabadsági fok esetében, amikor

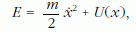
az (1) igazolása különösen egyszerű:

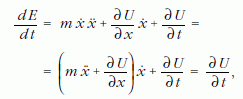
mert

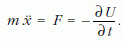
Lineáris harmonikus oszcillátorra

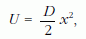
ezért

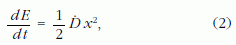
ahol D a direkciós "állandó", amely most függ az időtől. Ha ez a függés olyan gyenge, hogy a rezgés T periódusa alatt a D megváltozása elhanyagolhatóan kicsi, akkor a (2) egyenletet a t időpont körül átlagolhatjuk az éppen aktuális T(t) periódusidőre. Az x² ezalatt egy teljes periódust változik, és a négyzetének az átlaga a mozgás t-beli A(t) amplitúdó négyzetének felével egyenlő:

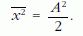
Az átlagolás után ezért (2) a

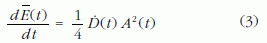
képletbe megy át, amelyben 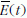az energia átlaga a t pillanat körüli egy periódusnyi időintervallumra. Mikor a D változása olyan lassú, hogy egy periódus alatt eltekinthetünk tőle, 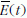ugyanúgy függ A(t)-től, mint amikor a D konstans:

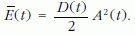
Mivel D = mω², ezért konstans m-nél a körfrekvencia is gyengén függ az időtől, és így 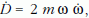valamint

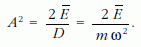
Ezt a két képletet (3)-ba írva az

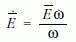
összefüggésre jutunk, amely az 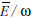arány időbeli állandóságát kifejező

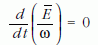
képlettel ekvivalens. Az 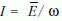arányt Ehrenfest – Einstein javaslatára – adiabatikus invariánsnak nevezte el. Ezt a terminológiát (és az I jelölést) használjuk általában a dinamikai mennyiségekből képzett olyan kifejezésekre, amelyek a rendszer paramétereinek lassú változtatásakor megtartják állandó értéküket.

A matematikai ingára áttérve azt látjuk, hogy az inga

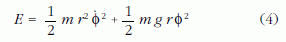
lengési energiájának mindkét tagja függ az inga r hosszától, amely a feladat lassan változó paramétere, és így

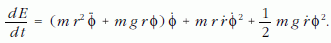
A mozgásegyenlet most 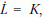ahol L = m r² φ a perdület (impulzusnyomaték), K = - m g r sinφ ≈ m g r φ pedig a forgatónyomaték. A φ-t szorzó zárójelre a mozgásegyenletből most nem nullát, hanem az

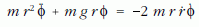
képletet kapjuk. Ennek következtében

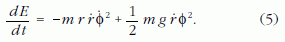
A gondolatmenet további része ugyanolyan, mint a lineáris harmonikus oszcillátoré. Ha a lengés amplitúdója Φ, akkor az energiája

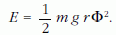
Az egy periódusra történő átlagolás eredménye pedig

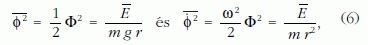
mert, mint tudjuk,

Mindezt behelyettesítve az átlagolt (5) formulába, azű

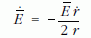
képletre jutunk, amely

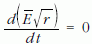
alakba írható át és az 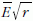szorzat adiabatikus invarianciáját fejezi ki. A (7) alapján az 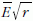adiabatikus állandósága azonban egyenértékű az 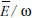hányados adiabatikus invarianciájával. Ezt kellett igazolnunk.

Az adiabatikus invariáns és az energiamegmaradás

Képzeljünk el egy fonálingát, amely a mennyezetről lóg le, és a szál egy lyukon keresztül felmegy a padlásra, ahol egy ember tartja. Tegyük fel, hogy az ember elkezdi nagyon lassan felfelé húzni (vagy lefelé engedni) az ingát. Mekkora ΔW munkát végez, miközben az inga fonálhossza r₁-ről r₂-re változik?

Amikor az inga hossza r-ről (r+dr)-re változik, az ember által végzett munka

-rel egyenlő. Az F_k a kötélerő nagysága, pozitív szám. Mivel az inga lengésben van, a kötélerőhöz az mgcosφ súlyerőn kívül az m rφ² centrifugális erő is járulékot ad:

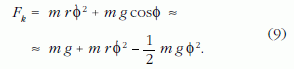
A feltevés szerint az ember olyan lassan húzza (vagy engedi) a kötelet, hogy teljesül az adiabatikusság feltétele: az inga egy lengési periódusa alatt a kötélhossz változása elhanyagolhatóan kicsi. A kötélerő egy periódusra történő átlagolását (9) alapján könnyen elvégezhetjük, mert a jobb oldalon fellépő átlagokat a (6)-ban már kiszámítottuk. Eszerint

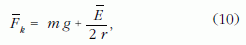
következésképpen

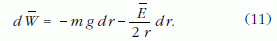
A ΔW kiszámításához ezt a képletet kell integrálni r₁-től r₂-ig. A lengés 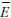egy periódusra átlagolt energiája azonban függ r-től, ezért az integráláshoz ismernünk kell az 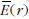függvényt.

Adiabatikus esetben az 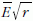szorzat állandósága az integrálást valójában triviálissá teszi. A (11) ekkor ugyanis

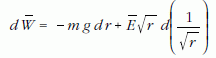
alakban írható, amelynek integrálja

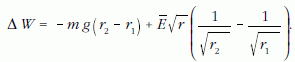
Az 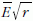a folyamat során nem változik, ezért helyettesíthetjük akár

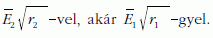
Amikor 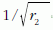-vel szorzódik az első, amikor pedig 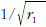-gyel, a második lehetőséget választjuk. Így

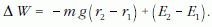
Ez a képlet biztosan korrekt, mert az energiamegmaradást fejezi ki az ingából és a kötelet húzó emberből álló rendszerre a Föld nehézségi erőterében. Ezzel demonstráltuk, hogy a matematikai ingánál 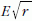adiabatikus invarianciája összhangban van ezzel a tétellel.

A csigainga²

A csigainga olyan állócsiga, amelynek kötélvégei fonálingává vannak kiképezve (1. ábra). Ez egy három szabadsági fokú rendszer, amelynek a helyzetét a két inga α₁, α₂ kitérése, valamint a csiga φ elfordulási szöge jellemzi. Ez utóbbi helyett azonban célszerűbb a

változó használata, amellyel r₁, r₂ így fejezhető ki:

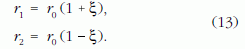
Az r₀ az r₁ és az r₂ félösszege, amely állandó érték. A φ és a ξ között a

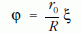
képlet adja meg a kapcsolatot, amely a nyilvánvaló dr₁ = -dr₂ = Rdφ következménye. A rendszer nem integrálható, egyetlen mozgásintegrálja az energia, ezért arra kell számítanunk, hogy a mozgása kaotikus. Csak annyit lehet róla mondani, hogy a nyugalmi állapota közömbös egyensúlyi helyzet: a legkisebb lökésre a kötél leszalad a csigáról.

Tegyük fel azonban, hogy bizonyos kezdőfeltételekhez tartozó mozgás során a csiga forgása olyan lassú (ξ olyan kicsi), az ingák lengése pedig olyan gyors, hogy az r₁, r₂ fonálhosszak változása adiabatikusnak tekinthető. Ebben az esetben a ξ ingadozni fog egy minimális és maximális érték között. Ez abból következik, hogy az

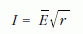
adiabatikus invariáns állandósága miatt (6) következtében a centrifugális erő annál kisebb, minél hosszabb a szál:

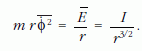
Amikor például r₁ nő, akkor az 1. ingára ható centrifugális erő csökken, a 2. ingára ható pedig nő, és ez a tendencia a csiga forgásirányának megfordulásához vezethet. Ekkor az ingák lengése stabilizálja a rendszert.

Amikor az adiabatikusság teljesül, a rendszer integrálhatóvá válik. Ez az energiaképlet alapján látható be. A csigainga energiája három tagot tartalmaz: a két inga lengése, valamint az ingadozás energiáját (a potenciális energiával nem kell törődnünk, mert konstans: mg(r₁+r₂) = 2mgr₀):

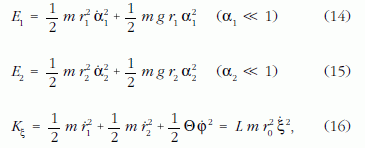
ahol Θ a csiga tehetetlenségi nyomatéka, és

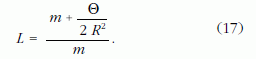
Adiabatikus közelítésben azonban

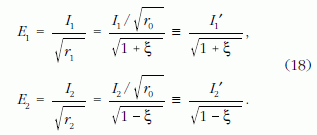
Ezekben a képletekben az I₁', I₂' mennyiségek konstansok, amelyeket a kezdőfeltételek határoznak meg. A rendszer energiájára ebben a közelítésben tehát az E = K_ξ+U_eff (ξ) képletet nyerjük, amely egy 1-szabadsági fokú objektum mozgását írja le az

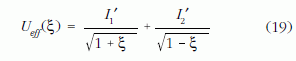
effektív potenciálban (2. ábra).

Az ilyen típusú feladatok mindig megoldhatók. A függőleges tengely E pontján keresztül párhuzamost rajzolunk a vízszintes tengellyel. Ez a ξ_min és a ξ_max pontokban metszi az U_eff (ξ) görbét. Ennek következtében az adott E energián az ingadozás a ξ_min ≤ ξ ≤ ξ_max tartományban fog történni. Az ingadozás periódusidejének felét úgy számíthatjuk ki, hogy az

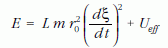
képletet megoldjuk dt -re és integráljuk az ingadozás tartományára:

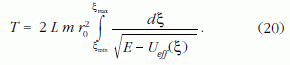
Mint látjuk, az ingadozás annál "lomhább", minél nagyobb az L paraméter, amelyet emiatt a rendszer lomhaságának nevezhetünk. Az adiabatikus közelítés annál jobb, minél lassúbb az ingadozás, vagyis minél nagyobb az L.

A lengések körfrekvenciája az ingadozás következtében folyamatosan nő és csökken valamilyen konstans ω1 és ω2 érték körül. Ezeket az értékeket is a kezdőfeltételek határozzák meg. Az adiabatikussághoz az kell, hogy ezek sokkal nagyobbak legyenek, mint az ingadozás

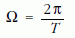
körfrekvenciája.

Amikor az adiabatikusság feltételei teljesülnek, az inga valóban periodikus ingadozásokat végez a (20) által meghatározott periódusidővel. A 3. ábrán3 a folytonos görbe a pontos mozgásegyenlet alapján történő számítás eredménye, amelyre szorosan illeszkednek az adiabatikus közelítés pontjai. A vízszintes tengelyen s = ω₀t a dimenziótlanított idő (ω₀ = (g / r₀)^1/2) Mint látható, az ingadozás tényleg periodikus és a periódus megegyezik a (20)-ból számítható értékkel. A görbe csipkézettsége az ingák lengésének következménye. Az adiabatikus közelítés ezt kisimítja. Azt várnánk, hogy az ingadozás szigorú periodikussága, amely egy közelítő eljárás, az adiabatikus approximáció következménye, az idő előrehaladtával fokozatosan elromlik, de a pontos mozgásegyenletek numerikus megoldásában ennek semmi jele.

Választhatók azonban olyan kezdőfeltételek, amelyeknél szintén elvárható volna az adiabatikusság teljesülése, a pontos mozgásegyenletek megoldása mégsem periodikus. Ilyen esetre vonatkozik a 4. ábra, amelyen szintén a folytonos görbe a pontos megoldás, a pontok pedig az adiabatikus közelítés. A magyarázat valószínűleg az ω₂/ω₁ arányban keresendő. A 4. ábra esetében ez az arány 1-gyel egyenlő és ez azt sugallja, hogy rezonáns kölcsönhatás léphet fel a két inga között, amely elrontja az ingák I₁, I₂ adiabatikus invariánsainak időbeli állandóságát. A részletesebb analízis azt bizonyítja, hogy ebben az esetben az ingadozásnak megfelelő időskálán lassú "lebegés" jön létre a két invariáns között (lásd az 5. ábrát, amelyek dimenziótlanított invariánsokra vonatkoznak). Amikor ω₂/ω₁ = 2, az ingák kölcsönhatása – úgy látszik – nem vezet az adiabatikus invariánsok szisztematikus változásához.

Összefoglalva megállapíthatjuk, hogy az inga mozgása, az előzetes várakozással ellentétben, nem mindig kaotikus, mert adott paraméterek mellett a kezdőfeltételek bizonyos tartományában a két adiabatikus invariáns két új mozgásállandó szerepét tölti be az energia mellett. Noha ezek bizonyos értelemben csak közelítően mozgásállandók, ezt a funkciójukat a várhatónál sokkal sikeresebben teljesítik. Érdekes lenne meghatározni e tartomány határait a fázistérben.

_______________

1. Planck a Kirchhoff-tételnek abból a következményéből indult ki, hogy a hőmérsékleti sugárzás spektruma független az üreg falának anyagi minőségétől, ezért – legegyszerűbb lehetőségként – a falat minden frekvencián egy-egy elektromosan töltött harmonikus oszcillátorral helyettesítette.
2. A csigainga részletes matematikai elmélete a Kettős adiabatikus inga című dolgozatomban található meg a honlapomon (hrasko. com/peter). Korábban ezt az érdekes objektumot tudomásom szerint még nem tanulmányozták.