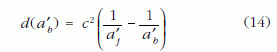
Fizikai Szemle honlap |
Tartalomjegyzék |
Bokor Nándor
BME Fizika Tanszék
Rövid kitérő a nyugalmi hossz fogalmáról és arról, mit értettünk eddig a sajáthossz fogalma alatt. Az olvasónak feltűnhetett, hogy a cikkben eddig kizárólag a "sajáthossz" kifejezést használtam az elterjedtebb "nyugalmi hossz" helyett. Szigorúan véve csak akkor van értelme egy adott tárgy (esetünkben például a cérna) nyugalmi hosszáról beszélni, ha a tárgy pontjai egymáshoz képest nyugalomban vannak (másképpen megfogalmazva: ha mindig létezik olyan inerciarendszer, amelyben a cérna összes pontja éppen áll). Ha a cérna végei például a 8. ábra b* és j jelű görbéi szerint mozognak, akkor ez nem teljesül (ezért szakad el a cérna), tehát a nyugalmi hossz fogalma ilyenkor nem értelmezhető.
A "sajáthossz" elnevezésre való áttérés önmagában a fogalmi nehézséget természetesen nem oldaná meg, mégis a sajáthossz definíciója értelmesen kiterjeszthető az olyan esetekre is, mint a 8. ábra b* és j jelű görbéi. Az új definíció szerint például sajáthossz alatt érthetjük mindig azt a cérnahosszt, amelyet a jobb oldali cérnavég pillanatnyi nyugalmi inerciarendszerében mérünk. Ebben az inerciarendszerben a jobb oldali cérnavég áll, a bal oldali pedig akár éppen távolodhat is tőle (ekkor a cérna egyre jobban megfeszül), vagy közeledhet hozzá (és a cérna meglazul). Ez a kibővített definíció természetesen magában foglalja a nyugalmi hossz fogalmát is (amikor az értelmezhető).
A kritikus sajátgyorsulásra vonatkozó számoláshoz hasonló módon, a (11) egyenletből kapható meg egy objektum nyugalmi hosszára vonatkozó elvi felső limit. Az egyenletből d-t kifejezve, mint a'b függvényét, a
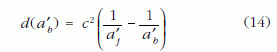
összefüggéshez jutunk. (Itt tehát a jobb oldali cérnavég a'j sajátgyorsulását adott konstans értékűnek feltételezzük.) A függvény menetét a 11. ábra mutatja. Az ábráról leolvasható, hogy a bal oldali vég adott gyorsulása mellett mekkora konstans d sajáthosszúsággal rendelkezhet a cérna. Ahogy a bal oldali cérnavég sajátgyorsulása végtelenhez közelít, a még éppen állandó megfeszítettségi állapotban tartható cérna sajáthossza véges értékhez, c2/a'j-hez tart.
Ilyenkor, amikor a a sajáthossz konstans, jogos a nyugalmi hossz megnevezés, hiszen mindig található olyan inerciarendszer, amelyben a teljes cérna éppen áll. A

tehát a nyugalmi hosszra vonatkozó felső korlátot adja meg. Csak ennél kisebb nyugalmi hosszal rendelkezhet egy olyan, jobb felé mozgó objektum, amelynek a jobb oldali vége adott a'j sajátgyorsulással mozog [2]. Ha az objektum kezdeti hossza dmax-ot eléri vagy annál nagyobb, akkor – a jobb oldali vég a'j gyorsulású mozgása esetén – a bal oldali végnek még végtelen sajátgyorsulás sem elég ahhoz, hogy az objektum sajáthosszát változatlan értéken tartsa. Ezzel a cikk elején említett 2. gondolatkísérlet eredménye is érthetővé válik. (A számadatok ellenőrzését ismét az olvasóra bízom.)
Első hallásra nagyon meglepő, hogy egyáltalán létezik ilyenfajta felső korlát egy objektum nyugalmi hosszára. Megnyugtatásul még egy érv: ha nem létezne ez a felső korlát, akkor az alábbi, úgynevezett Warnick-paradoxonra [2] jutnánk: Warnick-paradoxon: egy L hosszúságú űrhajó nyugalomból mozgásba lendül. Az űrhajó orra állandó gyorsulással – x0 távolságon, t0 idő alatt – akkora sebességre gyorsul, hogy az űrhajó mozgási hossza a Lorentz-kontrakció révén – mondjuk – éppen felére csökken. A laboratóriumi rendszerből mérve az űrhajó hátuljának tehát összesen x0+L/2 távolságot kellett megtennie t0 idő alatt. Az űrhajó végének
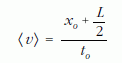
átlagsebessége – mivel az űrhajó L hosszát nem korlátozza semmi – tetszolegesen nagy lehet, például a fénysebességet is meghaladhatja. (Ez – mint ismert – súlyos logikai ellentmondásokhoz vezetne, például ilyen űrhajók hátulján ülve időutazást tehetnénk a múltba, és meggátolhatnánk saját születésünket.)
A Warnick-paradoxon megoldása a fentiek szerint világos: az űrhajó hosszára igenis létezik felső korlát, L nem lehet tetszőlegesen nagy. (Természetesen azt semmi sem gátolja meg, hogy az űrhajót a gyárban tetszőlegesen hosszúra építsék; arról van csak szó, hogy nem érdemes bizonyos űrhajóhossznál nagyobbat építeni, mert a hátulja nem fogja tudni követni az elejét – nem technológiai, hanem téridő-geometriai okokból! – és az űrhajó szétszakad.)
Az állandó sajáthosszúságú cérna bal oldali és jobb oldali vége eltérő alakú világvonalat követ (9. ábra), és ez azt sejteti, hogy a cérna két vége eltérő ütemben öregedik. Az alábbi részletes számolás megerősíti ezt a sejtést.
Mint láttuk, egy a' sajátgyorsulással mozgó tömegpont világvonala az
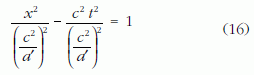
hiperbola. A sík téridő jól ismert
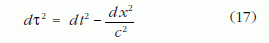
metrikus egyenlete ugyanakkor általánosan megad- ja, hogy két esemény között – amelyek (Minkowski-koordinátákban kifejezve) kis dt időbeli és dx térbeli távolságra történnek – mekkora dτ sajátidő telik el, azaz mekkora időtartamot mér a két esemény között egy olyan megfigyelő, aki mindkét eseménynél jelen volt.
A (16) és (17) egyenletekből könnyen levezethető a t koordinátaidő és az x térbeli koordináta τ sajátidőtől való függése a (16) világvonal mentén:
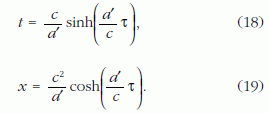
A 12. ábra Egy rúd három pontjának – például a cikk elején szerepelt 3. gondolatkísérletben fényévrudat szállító űrhajók közül háromnak – világvonalát ábrázolja, miközben a rúd nyugalmi hossza állandó marad. A világvonalakon a (18) és (19) összefüggéseknek megfelelően jelöltem be, és számoztam meg az egyes űrhajósok karóráján mutatott egyenlő időközöket. Az ábrán az egyes pontok szürkeárnyalatai az adott fényévrúd-darabka aktuális színét is jelzik – mindegyik azonos (sajátidő-)ütemben változik fehérről feketére. A 12. ábrából érthetővé válik a 3. gondolatkísérlet eredménye. Az űrhajósok öregedése "balról jobbra gyorsul": az űrhajók egy adott pillanatnyi nyugalmi inerciarendszerében mindig a bal oldali űrhajós órája mutatja a legkevesebbet (ő a legfiatalabb, a hozzá közel eső rúddarab a legvilágosabb), és a jobb oldali űrhajós órája mutatja a legtöbbet (ő a legidősebb, a hozzá közel eső rúddarab a legsötétebb).
A 8. ábra három lehetséges mozgást is felvázol a bal oldali cérnavég számára. Mindhárom felvázolt mozgás álló helyzetből indul – csakúgy, mint a jobb oldali cérnavégé –, de gyorsulásuk eltérő. Kérdés: közeledik-e a bal oldali cérnavég a jobb oldalihoz, ha a b** világvonalat követi?
A végig nyugvó, laboratóriumi inerciarendszer megfigyelője számára – az ő nézőpontját mutatja a 8. ábra – úgy tűnik, a b** és j cérnavégek egyértelműen közelednek egymáshoz. Ezt – amellett, hogy "az ábrából látszik" – két, mérésen alapuló érvvel is alá tudja támasztani:
Láttuk ugyanakkor, hogy a cérna sajáthossza akkor változatlan, ha a végek a b és j világvonalakat követik. Kicsit körülményesebb megfogalmazásban: a jobb oldali cérnavég mindig a pillanatnyi nyugvó inerciarendszereiben méri magától a bal oldali cérnavég távolságát, és ezek a távolságmérések akkor szolgáltatnak állandó értéket, ha a bal oldali vég a b világvonalon halad. Ha a bal oldali vég ehelyett a lomhább b** világvonalat követi, akkor a cérnavégek távolsága a jobb oldali vég τ sajátidejének függvényében monoton nő, azaz a cérnavégek egyre távolodnak.
Hogyan lehetséges, hogy két tömegpont folyamatosan közeledik is egymáshoz, meg folyamatosan távolodik is egymástól (nézőponttól függően)? Lehet-e mindkét állítás helyes? Esetleg tudjuk-e úgy definiálni a közeledés/távolodás fogalmát, hogy megszűnjön ez az értelmezésbeli kettősség?
Vannak ehhez hasonló jelenségek a relativitáselméletben, ilyen például két esemény sorrendje. Ha az események elég messze vannak egymástól térben, és elég közel időben (azaz, ha úgynevezett térszerű intervallum választja el őket), akkor sorrendjük nem invariáns; előfordul, hogy különböző inerciarendszerek eltérő választ adnak a két esemény sorrendjét firtató kérdésre.
Legitim megoldás, ha a közeledés/távolodás fogalmát is a relativitáselmélet nem invariáns fogalmai közé soroljuk. Nem kell azonban feltétlenül elsietnünk ezt a következtetést, legalábbis abban az egyszerű esetben – mint amilyenek a föntiek is – amikor a közeledés/távolodás "monoton" (például egyik mozgás sem oszcilláló).
Először is: van, ami a közeledéssel/távolodással kapcsolatban abszolút értelemben eldönthető. Ha például a két tömegpont mozgását ábrázoló világvonalak metszik egymást (vagyis a tömegpontok összeütköznek), akkor nem lehet igaza annak, aki azt állítja, hogy a tömegpontok folyamatosan távolodnak egymástól. A 8. ábra ugyan nem ilyen esetet mutat (ott a b** és j világvonalak nem metszik egymást, csak – a nyugvó inerciarendszer szerint – aszimptotikusan tartanak egymáshoz), de ott is van egy segítségünk: maga a cérna. A két tömegpontot ugyanis mindig öszszeköthetjük – legalább képzeletben – egy olyan cérnával (vagy rúddal), amelynek hosszát úgy választjuk meg, hogy a kezdő időpillanatban – amikor mind a két tömegpont állt a nyugvó inerciarendszerben – éppen megfeszüljön (rúd esetén se nyomó-, se húzófeszültség ne ébredjen benne). Ezek után a közeledést, illetve távolodást így definiálhatjuk: a két tömegpont közeledik egymáshoz, ha a cérna meglazul (ha a rúdban nyomó feszültség ébred), és távolodik, ha a cérna megfeszül, majd elszakad (ha a rúd megfeszül, majd széttörik). E definíció előnye, hogy nem igényel globális nézőpontot; nem kell, hogy a két távoli tömegpont mozgását egyszerre nyomon kövessük (hiszen az eredeti bonyodalom éppen az "egyszerre" szó abszolút módon értelmezhetetlen jellegéből származott), hanem csak lokális megfigyelésre van szükség: a cérna/rúd egy darabkájának a viselkedését kell megfigyelni. Ilyen módon a közeledés/távolodás fogalma valóban invariánssá válik: abban nincsen vita a különböző megfigyelők között, hogy a cérna elszakadt-e vagy sem. A fenti definíciót használva a 8. ábra nyugvó megfigyelője is kénytelen azt a következtetést levonni, hogy a b** és a j világvonalakon haladó tömegpontok távolodnak egymástól, hiszen a két tömegpontot összekötő cérna viselkedéséből számára is ez következik.
Sokszor segít a relativitáselmélet meglepő jelenségeinek megértésében, ha intuíciónk számára sokkal ismerősebb terepre vonulunk, és megpróbáljuk megkeresni a jelenség analógiáját az euklideszi síkon.
A nyugalmi hossz és a sajátgyorsulás fent levezetett – és szemléletünk számára meglepő – elvi korlátjára a következő euklideszi analógia kínálkozik:
Sík terepen egy kerékpár rj sugarú (Gj = 1/rj görbületű) körpályán gurul. A kerékpár pályáját a 13. ábra szemlélteti. A kerékpáros a pályára merőlegesen balra kinyújt egy d hosszúságú rudat. Egy másik kerékpáros feladata az, hogy úgy tartsa a rúd másik végét, hogy a rúd orientációja mindig az első kerékpáros pályájára merőleges maradjon. Az is követelmény, hogy a két kerékpáros azonos irányba nézzen
Ismételjük el a fenti mondatok megfelelőit a cikkben tárgyalt relativisztikus jelenség leírására:
Sík téridőben egy űrhajó aj sajátgyorsulással jobbra indul. Az űrhajóhoz rögzítjük egy d hosszúságú rúd jobb oldali végét. (A rúd hosszát az űrhajós, aki pillanatnyi nyugalmi inerciarendszerének időtengelye mentén mozog, ezen inerciarendszer x tengelye mentén, az időtengelyre "merőlegesen" méri.) Egy másik űrhajónak az a feladata, hogy tartsa a rúd bal oldali végét, de közben a rúdban se húzó-, se nyomófeszültség ne ébredjen. A két űrhajó természetesen a téridőnek "azonos irányába néz" – a múltból a jövő felé.
A 2. gondolatkísérlet tárgyalásakor, valamint magában a Dewan–Beran gondolatkísérletben – a szerzőkhöz hasonlóan – hallgatólagosan figyelmen kívül hagytam a cérna vagy rúd belső állapotváltozásait (például a gyorsulási szakaszok alatt történő rugalmas vagy rugalmatlan alakváltozásokat, a mechanikai hullámok kialakulását stb.). Csak ezen egyszerűsítő és erősen idealizáló feltevés elfogadásával állíthatjuk, hogy a bal oldali vég és a jobb oldali vég egymáshoz képesti nyugalmi helyzete egyben a nyugalmi hossz változatlanságát is jelenti, hiszen egy tárgy nyugalmi hossza függ a tárgy belső állapotától.