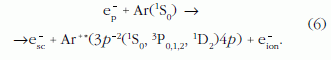Fizikai Szemle 2012/12. 411.o.
ATOMI BELSŐHÉJ-FOLYAMATOK VIZSGÁLATA
KOINCIDENCIA ELEKTRONSPEKTROMETRIÁVAL - II. RÉSZ
Paripás Béla, Palásthy Béla
Miskolci Egyetem, Fizikai Tanszék
A Fizikai Szemle 2012. novemberi számában megjelent
első részben az elméleti bevezetés és a mérőrendszer
bemutatása olvasható.
Néhány kísérleti eredmény
PCI-mérések
A PCI rövidítés az ütközés utáni kölcsönhatás angol
nevéből (post-collision interaction) képzett mozaikszó,
a vizsgált Auger-folyamat (1) különböző lépései során
keletkezett töltött részecskék Coulomb-kölcsönhatását
jelenti. Ebben a folyamatban a PCI energiacserét jelent
az első lépésben keletkezett ionizációs 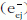 és szórt elektronok
és szórt elektronok 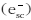 ,
valamint a második lépésben keletkezett
Auger-elektronok
,
valamint a második lépésben keletkezett
Auger-elektronok 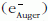 között
(1. ábra). Ez az
energiacsere az Auger-csúcsok alakjának torzulására és
maximumainak eltolódására vezet. Ez kísérletileg jól
mérhető, és a PCI-t leíró félklasszikus modell keretében
az úgynevezett aszimmetria-paraméter bevezetésével
kvantitatív módon is vizsgálható [2].
között
(1. ábra). Ez az
energiacsere az Auger-csúcsok alakjának torzulására és
maximumainak eltolódására vezet. Ez kísérletileg jól
mérhető, és a PCI-t leíró félklasszikus modell keretében
az úgynevezett aszimmetria-paraméter bevezetésével
kvantitatív módon is vizsgálható [2].
A PCI különösen erős a kis energiás ionizációs elektronokra,
ezeket "utoléri" a később keletkezett Auger-elektron.
Ez akkor következik be, ha az atomnak átadott
energia alig haladja meg az ionizációs energiát (5. ábra).
A modell szerint ilyenkor az aszimmetria-paraméter
lényegében csak az ionizációs elektron sebességének
nagyságától függ. Azaz végeredményben a PCI-t
a megmért elektronenergiák szinte teljesen meghatározzák,
a jórészt megméretlenül maradt sebességi irányok
alig befolyásolják. Az a) "ablakban" végzett mérés
során tehát a PCI lényegében irányfüggetlen, mértéke
kiszámítható, a kísérlettel jól összevethető. Ez az összevetés
azért is izgalmas, mert a nagyon lassú elektronok
félklasszikus leírása - a nagy hullámhosszuk miatt -
már ugyancsak kérdőjeles.
Az argon L2,3-M2,3M2,3 Auger-elektron spektrumát
500 eV nominális lövedékelektron-energiánál vettük
fel [3]. Ennél a primer energiánál az L3 és L2 belső
héjak ionizációs potenciálja fölötti többletenergia
251,4 eV, illetve 249,2 eV érték. Ez a többletenergia a
szórt lövedék és az ionizációs elektron között oszlik
szét. Az Auger-elektronok spektrumát a 248 eV energiájú
szórt elektronokkal koincidenciában vettük fel,
tehát az L3 és L2 belső héjak ionizációja során kibocsátott
elektronoknak névlegesen csak 3,4 eV, illetve 1,2
eV kinetikus energia marad. Ezek jelentősen különböző
értékek, a koincidencia-spektrumban a PCI a két
alhéjra tehát jelentősen eltér. A 6. ábrán az összegzett
teljes (nem koincidencia) és a koincidenciában mért
elektronspektrumok láthatók, amelyeknél a körülbelül
20%-os véletlen koincidenciát már levontuk. A
spektrum körülbelül 109 nagyságrendű beütést tartalmaz,
amelyet 15-25 nap alatt vettünk fel.
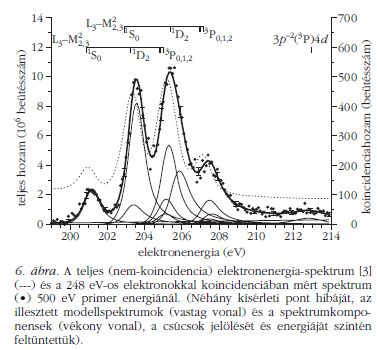
Az illesztés során a kvadratikus háttér levonása
után a PCI torzított csúcsalakot konvoláltuk a kísérleti
spektrométer átviteli függvénnyel. Először mindig a
teljes energiaspektrumot illesztettük. A modellspektrumban
a 10 diagram Auger-vonal intenzitásai és
energiái illesztendő paraméterek voltak, kivéve a tripletteket,
ahol az intenzitásarányokat és az energiakülönbségeket
az irodalomból [4] vettük. A teljes spektrum
10 csúcsának közös aszimmetria-paramétere is
egy illesztendő paraméter. A teljes spektrumok igen
jó statisztikája lehetővé tette a közel 20 független
paraméter egyidejű illesztését. A későbbiekben a kísérleti
érték alatt az illesztés eredményét értjük. A
koincidencia-spektrumok statisztikája azonban nem volt túl
jó, ezért az illesztendő paraméterek számát minimalizálnunk
kellett. Csak a két alhéj intenzitásait és
aszimmetria-paramétereit, a spektrométer átviteli függvény
szélességét és a háttér paramétereit illesztettük, a többi
paraméter értékét rögzítettük a teljes spektrum
illesztésénél kapott értéken.
A koincidencia-spektrum nagyenergiás végén
(212-214 eV) nem belső héj eredetű kis csúcs(ok)
figyelhető(k) meg. Az átadott energia és a kis csúcs(
ok) energiájának különbsége körülbelül 38-40 eV,
ami megfelelhet az Ar+*3p-2(1D
vagy 3P)3d vagy 4d
külső héj gerjesztett szatellitállapotoknak. Az ábrán a
212,7 eV-nál látható csúcs minden bizonnyal az
Ar+*3p-2(3P)4d 2D és 2P
csoportnak felel meg.
A két alhéjra számított átlagos aszimmetriaparaméter-
érték ennél az energiakombinációnál (figyelembe
véve a kibocsátott elektronok (5) szórású Gauss-eloszlását
is) -2,6, illetve -5,4. A kísérleti spektrumra legjobban
illeszkedő modellspektrum aszimmetria-paramétere
(amit kísérleti aszimmetria-paraméternek tekinthetünk)
a két alhéjra -2,0 (±0,1), illetve -4,12 (±0,4). Az
egyezés elég jó, különösen ha azt is figyelembe veszszük,
hogy az illesztett spektrum aszimmetria-paraméterének
nagysága szükségszerűen az átlagérték alatt
van [3]. Ezen eredményünk szerint a néhány eV-os
elektronok PCI-kölcsönhatásának félklasszikus leírása
még nem mond ellent a kísérleti adatoknak. A még
kisebb energiájúaké (Eej < 1 eV) azonban már igen,
ahogy ezt egy későbbi kísérletünkben [5] igazoltuk.
Elektronütközéses rezonáns Auger-mérések
Az elektronütközéses rezonáns Auger-folyamat az
elektronnal gerjesztett belső héj vakanciás atomi rezonancia
Auger-szerű elbomlását jelenti ((2), illetve 1. ábra
alsó része). Régebbi, nem-koincidencia méréseinkben
az argon belső héj ionizációjához tartozó igen kis
intenzitású szatellitvonalait egy speciális kiértékelési
folyamattal igyekeztünk a diagramvonalakról leválasztani
[6]. Ez részben sikerült is, megfigyeltük - többek
között - a 2p-1(2P3/2)4s
és 4p gerjesztéseket követő legvalószínűbb
(azaz 1D) átmeneteket az összes vizsgált
primer energián. Szelektív módszerekkel - ilyen az
(e,2e) módszer is - a kis intenzitású szatellitvonalak
kiemelhetők a spektrumból, lényegében felnagyíthatók.
Ezt a folyamatot azonban - a nyilvánvaló méréstechnikai
nehézségek miatt - ezzel a módszerrel se nagyon
szeretik vizsgálni a kísérleti fizikusok. Az elektronütközéses
adatok hiánya azért is szembeötlő, mert a
megfelelő fotongerjesztéses folyamatoknak (például
2p-1(2P3/2)4s)
könyvtárnyi az irodalma. A dipól tiltott
gerjesztések ráadásul fotonnal nem is valósíthatók meg,
így ezek rezonáns Auger-spektrumaira nincs is mérési
adat (a miénket kivéve). Jelen cikkben ez utóbbi kategóriából
mutatjuk be az argon 2p-1(2P3/2)4p
elektronütközéses rezonáns Auger-spektrumát [7].
Méréseinket az 5. ábra b) átadott energia "ablakában"
végeztük, amelyben Etr = 245,7 eV, ami a 344,9
eV primer energia és a 99,2 eV koincidencia-feltétel
különbségeként adódik. (Megjegyezzük, hogy a (b)
ablak közepe egy kicsit alatta van a 2p-1(2P3/2)4p
gerjesztési
energiának, hogy a 2p-1(2P1/2)4s gerjesztést
mindenképpen elkerüljük.) Mielőtt azonban a kapott
koincidencia-spektrumot bemutatnánk, szólnunk kell
ezen mérés legnagyobb nehézségéről, a koincidenciaspektrum
direkt ionizációs hátteréről.
A (2) képlettel leírt rezonáns Auger-folyamat végállapotai
egyetlen lépésben, direkt módon is létre jöhetnek,
ezt semmiféle fizikai törvény nem tiltja:
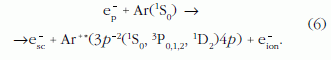
Ez a folyamat egy egyszeres direkt ionizáció, így a
második elektront most ionizációs elektronnak nevezzük.
Az egyszeres ionizáció nagy valószínűségű folyamat
(még ilyen különleges ion esetén is), így ezzel
mindenképpen számolnunk kell. Lényeges különbséget
jelenthetne az a tény, hogy most a végállapot kontinuumállapot
folytonos elektronenergia-spektrumokkal
(mert a végállapotbeli három részecske a többletenergián végtelen sokféleképpen osztozhat).
Koincidencia-mérésben
azonban rögzítjük az egyik elektron
energiáját, ami - az energia megmaradása és az ion
kis mozgási energiája miatt - vonalassá teszi a másik
elektron spektrumát is.
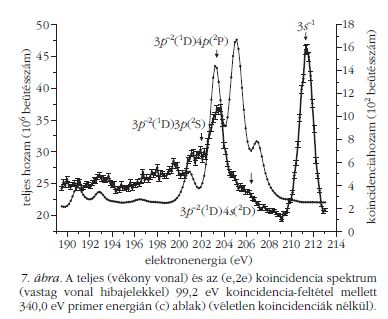
A másik lényeges különbség az, hogy a direkt folyamat
valószínűségének energiafüggése sokkal lassúbb,
mint a rezonancia-szerű kétlépéses folyamaté.
Különösen igaz ez a mi mérési körülményeink között,
amikor a primer energia egy nagyságrenddel meghaladja
az ionállapotét. Az 5. ábrán szereplő c) ablakban
mérve tehát ugyanazt a direkt spektrumot kell
kapnunk, mint a néhány eV távolságra lévő b) ablakban.
A mért spektrumok eltérései kizárólag az indirekt
folyamattól származhatnak. Másképpen fogalmazva a
c) ablakban mért spektrum a b) ablakban
mért rezonáns Auger-spektrum direkt ionizációs hátterét
jelenti, ami így levonható. Itt meg kell jegyeznünk
egyrészt azt, hogy a háttér levonása általános
gyakorlat, a direkt ionizációs hátteret egyszerű (nem
koincidencia) Auger-spektrum mérésekben is le szokás
vonni, ott azonban a háttér folytonos (általában
egyenessel közelíthető). Másrészt azt, hogy ez nem
mindig tehető meg, mert a direkt és indirekt folyamatoktól
származó elektronhozamok nem föltétlenül
additívak. Ugyanis az ugyanarra a végállapotra vezető
folyamatok között kvantummechanikai interferencia
is lehetséges. Ráadásul ez az interferencia akár jelentős
is lehet, mert a direkt és indirekt folyamatoktól
származó elektronhozamok közel egyenlők, ez esetleg
megkérdőjelezheti a háttér levonásának fenti
módszerét.
A direkt ionizációs háttér a 7. ábrán látható, legintenzívebb
vonalait beazonosítottuk.
Az elektronütközéssel gerjesztett Ar*(2p-1(2P3/2)4p
állapot lebomlása közben kibocsátott elektronok
spektrumát (8. ábra) tehát úgy kaphatjuk meg, hogy
a b) ablakban felvett koincidencia-spektrumból kivonjuk
a c) ablakban mért (és a 7. ábrán bemutatott)
direkt ionizációs hátteret. A kivonás előtt a koincidencia-
hozamokat természetesen normáltuk (itt most a
99,2 eV-os elektronok hozamára), a direkt ionizációs
hátteret pedig eltoltuk a primer energiák különbségével,
azaz 4,9 eV-tal.
A spektrumban a korábbi nem-koincidenciaméréseinkben
[6] talált vonal (az ábrán vastagon szedve) is
jól látható, az a spektrum domináns vonala. A bejelölt
1D végállapotú vonalak fölött 1,6 eV-tal a megfelelő 3P
vonalaknak is jelen kell lenniük. Az ábrákon ezek a
csúcsok látszanak is 210,2 eV környékén.
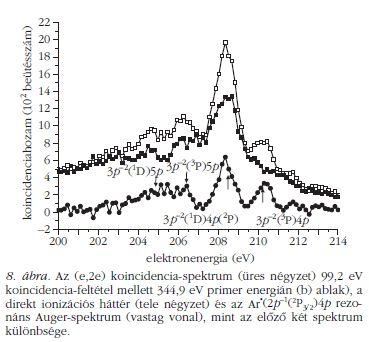
Korábban utaltunk rá, hogy a rezonáns Auger-folyamatban
a shake-up jelenséggel gyakran számolni
kell. Az ábrán 204,4 eV és 206 eV energiánál megjelenő
csúcsokról nagy bizonyossággal állíthatjuk, hogy a
2p → 4p gerjesztést követő rezonáns Auger-bomlás
(3p-2(1D2)5p) és
(3p-2(3P1)5p) végállapotaihoz tartoznak.
Számításaink azonban azt mutatják [8], hogy a
shake-up jelenségnek kisebbnek kellene lennie. Ez
fölveti annak lehetőségét is, hogy a 204-206,5 eV közötti
magas beütésszám részben a direkt és indirekt
folyamatok közötti kvantummechanikai interferencia
következményei. E kérdés tisztázására jelenleg is folynak
a méréseink.
Irodalom
- M. Yu. Kuchiev, S. A. Sheinermann: Resonant scattering with
low-velocity outgoing charged particles. J. Phys. B: At. Mol. Opt.
Phys.21 (1988) 2027 .
- B. Paripás, B. Palásthy, G. Vitéz, Z. Berényi: Post-collision interaction
measured by coincidence spectrometry in electron
impact Auger process. J. Phys. B: At. Mol. Opt. Phys. 41 (2008)
035201.
- Gy. Víkor, L. Tóth, S. Ricz, Á. Kövér, J. Végh, B. Sulik: Transition
energies and relative intensities of the Ar L2,3-MM diagram Auger
lines: a high-resolution study. Journal of Electr. Spectr. Rel.
Phen. 83 (1997) 235.
- B. Paripás, B. Palásthy: Post-collision interaction after electron
impact measured by (e,2e) coincidence technique. Nucl. Instr.
Meth. B 267 (2009) 275.
- B. Paripás, Gy. Víkor, S. Ricz: Observation of Electron Impact
Inner-Shell Excitation of Argon by means of Satellite Auger
Spectra. J. Phys. B: At. Mol. Opt. Phys. 30 (1997) 403.
- B. Paripás, B. Palásthy, M. Zitnik, K. Tőkési: Experimental (e,2e)
study of resonant Auger states of Ar. Nucl. Instr. Meth. B 279
(2012) 66.
- B. Paripás, B. Palásthy, M. Stuhec, M. Zitnik: Resonant Auger
decay of Ar 2p-1
3/24s and 2p-1
3/24p states excited by electron impact.
Phys. Rev. A 82 (2010) 032508-1-10.
____________________________
A kutatás a TÁMOP-4.2.1.B-10/2/KONV-2010-0001 jelű projekt részeként,
az Európai Unió támogatásával, az Európai Szociális Alap
társfinanszírozásával valósul meg.
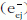 és szórt elektronok
és szórt elektronok 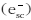 ,
valamint a második lépésben keletkezett
Auger-elektronok
,
valamint a második lépésben keletkezett
Auger-elektronok 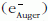 között
(1. ábra). Ez az
energiacsere az Auger-csúcsok alakjának torzulására és
maximumainak eltolódására vezet. Ez kísérletileg jól
mérhető, és a PCI-t leíró félklasszikus modell keretében
az úgynevezett aszimmetria-paraméter bevezetésével
kvantitatív módon is vizsgálható [2].
között
(1. ábra). Ez az
energiacsere az Auger-csúcsok alakjának torzulására és
maximumainak eltolódására vezet. Ez kísérletileg jól
mérhető, és a PCI-t leíró félklasszikus modell keretében
az úgynevezett aszimmetria-paraméter bevezetésével
kvantitatív módon is vizsgálható [2].