A 2012. ÉVI EÖTVÖS-VERSENY ÜNNEPÉLYES EREDMÉNYHIRDETÉSE

Tichy-Rács Ádám
BME OMIKK

A 2012. évi Eötvös-versenyt október 12-én rendezték, az eredményhirdetésre november 16-án délután került sor az ELTE konferenciatermében.

Radnai Gyula, a Versenybizottság elnöke letette fehér köpenyét és köszöntötte a megjelenteket. Megemlékezett az 50 éve elhunyt Nagy L. József piarista tanárról, aki igen sokat tett a korabeli KöMaL, valamint a Fizikai és Kémiai Didaktikai Lapok megalapításáért, tankönyveket írt. A KöMaL novemberi számában is megemlékeztek róla. A már több éves gyakorlatnak megfelelően - a részletes eredmények izgatottan várt ismertetését megelőzve - az 50, illetve a 25 év előtti Eötvös-versenyről való megemlékezésre került sor.

Eötvös-verseny, 1962

1. feladat (Bártfai Tamás)
Három darab R = 5 cm rádiuszú, Q = 1 kp súlyú golyó lóg egy-egy l = 7,5 cm hosszú fonálon. Mindhárom fonál közös pontban van felfüggesztve. A három egymásnak támaszkodó golyóra középen r = 2,5 cm rádiuszú golyót helyezünk. Legfeljebb mennyi lehet e golyó q súlya, hogy át ne essen a három lógó golyó között? Súrlódás nincs.

2. feladat (Károlyházy Frigyes)
Egyenletes vastagságú, azonos anyagú bádoglemezből három üres, egyenes körhenger készült. Az első átmérője 5 cm, magassága 5 cm; a második átmérője 10 cm, magassága 5 cm, a harmadik átmérője 5 cm, magassága 7,5 cm. Megvizsgáljuk a hengerek elektromos ellenállását olyan módon, hogy a mérőműszer huzalvégeit a hengerek alap és fedő körlapjainak középpontjaihoz érintjük. Melyik henger ellenállása a legnagyobb, és melyiké a legkisebb?

3. feladat (Vermes Miklós)
Tőlünk 400 méterre 1 méter átmérőjű kör alakú üvegablak van, amely a róla visszaverődő napsugaraktól megcsillan. Legfeljebb meddig tart ez a jelenség?

Radnai Gyula felidézte, hogy az első feladat szerinti elrendezést Vermes Miklós elkészítette, és a modell ma is megtekinthető a csepeli Jedlik Gimnáziumban.

1962-ben csak érettségizettek vehettek részt a versenyen, amin 51 budapesti és 41 vidéki tanuló indult. Közülük összevont I. és II. díjat nyert Nagy Dénes Lajos és Szegi András, a budapesti II. Rákóczi Ferenc Gimnázium tanulói, Lantossy Károly tanítványai. III. díjat nyert Máté Eörs, a szegedi Radnóti Miklós Gimnázium tanulója, Bábiczkiné Gremsperger Katalin tanítványa. Első dicséretet kapott Góth László a budapesti Könyves Kálmán Gimnázium tanulója, Turtóczki László tanítványa, második dicséretet kapott Simonovits Miklós, a budapesti Radnóti Miklós Gimnázium tanulója, Borszéki Erzsébet tanítványa.

Az ötvenedik évfordulón mind az öten megjelentek, közösen emlékeztek a versenyre, a több évet végigkísérő versengésre, de ami még fontosabb, a barátságra, ami a mai napig megmaradt. Simonovits Miklós arról beszélt, hogy mennyiben térnek el a középiskolai és egyetemi feladatok, és milyen minőségi változást jelentenek a felnőtt életpálya problémái. "Az ember a gimnáziumi versenyeken nagyon sok pozitívumot kap, nagyon sok mindent megtanul, nagyon jól motivált. Ezeknél a versenyeknél mindig jön egy jó tanár, odateszi a feladatot, amit meg kell oldanunk, ez valami. Az egyetemen azt lehetett látni, hogy a gimnáziumban kialakult sorrendek átalakulnak. Sokkal fontosabb, hogy az ember megtanulja kiválasztani, hogy őt mi érdekli, és milyen irányba megy. Az életben ez másképpen megy. Amikor befejeztük az egyetemet, akkor még egy váltás volt." Szegi András röviden bemutatta a második versenyfeladatban ismertetett probléma "hivatalos" megoldását, és a tényleges mérés elvégzésének problémáját. Végül Nagy Dénes Lajos köszönetet mondott az első fizikaszakkört vezető, és a teremben most is ott ülő tanárának, Holics Lászlónak.

A versenybizottság figyelmét Máté Eörs hívta fel egy hiányosságra, amikor felidézte a korabeli eredményhirdetést: "(A versenyek után) soha nem kaptam visszajelzést arról, hogy mit rontottam el… »Úgy tűnik, hogy mindhárom feladatot jól megoldotta Máté Eörs. Harmadik díj.« Nem tudom, mi volt rossz. Azóta eltelt ötven év."

A huszonöt évvel ezelőtti Eötvös-verseny feladatai az alábbiak voltak:

Eötvös-verseny, 1987

1. feladat (Vermes Miklós)
Különböző hajlásszögű lejtőkről golyót gurítunk le. A lejtők magassága egyenlő. A csúszó súrlódási együttható µ = 0,1. Mekkora hajlásszögű lejtőnél fejlődik a legtöbb meleg?

2. feladat (Károlyházy Frigyes)
Egy henger terét egy dugattyú választja ketté. Minden alkatrész jó hővezető és a hőmérséklet 100 °C. A bal oldali 1 köbdeciméteres részben hélium van. A jobb oldali 1 köbdeciméteres részben vízgőz és 0,588 gramm folyékony víz van. A nyomás 1 atmoszféra. Ezután változtatjuk a hőmérsékletet a lehető legalacsonyabbtól a legmagasabbig. Vizsgáljuk meg, hogyan függ a dugattyú helyzete a hőmérséklettől!

3. feladat (Károlyházy Frigyes)
Egy kartonhengertől meghatározott távolságra, vékony fonálra egy lágyvasdarabkát függesztünk. A hengerre huzalból tekercset csévélünk, és erre egy meghatározott váltófeszültséget kapcsolunk. A vasdarabka kissé elmozdul. Hogy a hatást megnöveljük, a hengerre kétszer annyi menetet csévélünk. Mit fogunk tapasztalni?

Az 1987-es versenyen Budapesten 121, vidéken 146 versenyző vett részt. Nem volt olyan versenyző, aki mind a három feladatot hibátlanul megoldotta, így első díjat nem adtak ki. Második díjat nyert Gyuris Viktor honvéd (Fazekas Mihály Gimnázium, Budapest; tanára Horváth Gábor), Nagy Gergely, a BME hallgatója (József Attila Gimnázium, Budapest, Sarkadi Ildikó) és Páczelt Ferenc tanuló (Móricz Zsigmond Gimnázium, Budapest, Sikó Attiláné ). Harmadik díjat nyert Cynolter Gábor honvéd, (Fazekas Mihály Gimnázium, Budapest, Horváth Gábor), Fucskár Attila tanuló (Kaffka Margit Gimnázium, Budapest, Jánosi Ilona), Jakab Péter tanuló (Verseghy Ferenc Gimnázium, Szolnok, Sebestyén István ), Kégl Balázs tanuló (Apáczai Csere János Gimnázium, Budapest, Zsigri Ferenc), Kiss Tamás tanuló (József Attila Gimnázium, Budapest, Tóth Eszter ). Dicséretet kaptak Derényi Imre tanuló (Révay Miklós Gimnázium, Győr, Székely László), Lang András tanuló (Révay Miklós Gimnázium, Győr, Székely László, Bőnyi Mihály, Jagodits György). Elismerést kapott továbbá Balogh Péter ELTE TTK (I. László Gimnázium, Mezőkövesd, Rácz György), Szokoly Gyula honvéd (Fazekas Mihály Gimnázium, Budapest, Horváth Gábor).

Kiss Tamás arról mesélt, hogy Wigner Jenő az eredményhirdetés után nem sokkal ellátogatott a József Attila Gimnáziumba. Megemlékezett Békésy György Nobel-díjasról, aki a második világháború alatt saját kezűleg mentette a fizika tanszék műszereit.

Fucskár Attila elmondta, hogy ő a versenyeket valójában intelligenciatesztként tudja értelmezni. Az Eötvös-versenyen 1987-ben és 1988-ban szerepelt kiválóan. Szerette, hogy ez egy rövid verseny, három példát tartalmaz, amelyek nem evidens dolgok, valamit ki kell találni megoldáshoz. Ezzel ellentétben áll az OKTV sok feladata, ahol viszont mindig elszámolt valamit, és nem jutott döntőbe.

Derényi Imre fizikatanárára, osztályfőnökére és osztálytársaira, valamint pályaválasztására emlékezett. Cynolter Gábor a versenyek élményét elevenítette fel. Mesélt az előfelvételis honvédként Lentiben eltöltött időről, és arról, hogyan értek haza a versenyre. Szokoly Gyula a diákolimpiai szakkör vezetőjét, Honyek Gyulát említette, aki viszont felidézte, hogy az ő négy oldalon levezetett megoldása helyett Cynolter Gábor egyetlen sorban oldott meg egy feladatot. A visszaemlékezések után Radnai Gyula ismertette az idei Eötvös-verseny feladatait:

Eötvös-verseny, 2012

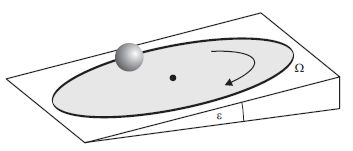
1. feladat (Vigh Máté)
Egy sík, érdes felületű, a vízszinteshez képest ? szögben döntött korong egyenletesen, Ω szögsebességgel forog. Egy bűvész a forgó korong közepére egy R sugarú, tömör gumilabdát helyez, majd megfelelő irányban elgurítja. A közönség legnagyobb ámulatára a labda középpontja ezután egyenes vonalú, egyenletes mozgást végez, amit mindaddig folytat, amíg a labda a forgó korong peremére ér. (A labda mindvégig tisztán gördül, a korong szögsebessége nem változik.) Adjunk fizikai magyarázatot a furcsa jelenségre! Milyen irányban és milyen kezdőfeltételekkel kell indítania a bűvésznek a labdát, hogy a mutatvány sikerüljön?

2. feladat (Radnai Gyula)
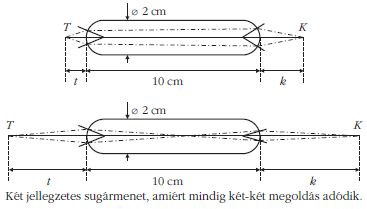
Egy 10 cm hosszú és 2 cm vastag, hengeres üvegrúd mindkét domború vége egy-egy félgömb. A rúd tengelye mentén, egyik végétől mekkora távolságra helyezzünk el egy pontszerű fényforrást a levegőben, ha azt akarjuk, hogy a rúd másik végétől a) ugyanakkora, b) kétszer akkora távolságra találkozzanak az onnan kilépő, a tengellyel kis szöget bezáró fénysugarak? Az üveg levegőre vonatkoztatott törésmutatója 1,5.

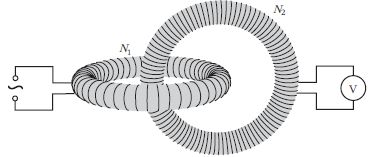
3. feladat (Vigh Máté)
Két ugyanolyan méretű, csak a menetszámukban különböző, egyenletes tekercselésű, N1 és N2 (> N1) menetes toroid tekercs egymásba van fűzve az ábra szerint. (A középkörök síkjai merőlegesek egymásra.)

1. ) Melyik tekercs kivezetései között indukálódik nagyobb feszültség, ha a másik tekercsben adott effektív áramerősségű és frekvenciájú váltakozó áram folyik?
2. ) Az N1 menetes tekercsre U effektív értékű, hálózati váltakozó feszültséget kapcsolunk, a másik (N2 menetes) tekercs kivezetéseire pedig ideálisnak tekinthető voltmérőt kötünk. Mekkora effektív feszültséget jelez a műszer? Legyen, mondjuk N1 = 100, N2 =900, U = 230 V!

A feladatok megoldását a Versenybizottság elnöke ismertette. (Ezek majd a Középiskolai Matematikai és Fizikai Lapokban jelennek meg.) Vigh Máté, a zsűri tagja bemutatta az első feladat ötletét adó, internetről levett felvételeket. A harmadik feladathoz Vankó Péter (BME TTK Fizika Tanszék) és Vigh Máté (ELTE TTK Komplex Rendszerek Fizikája Tanszék) mutatott be kísérletet.

Néhány gondolat a feladatok megoldásával kapcsolatban. Az első feladatban először azt kell belátni, hogy a golyót a forgó asztal középpontjából kell elindítani úgy, hogy éppen vízszintes síkban induljon el. Minden más esetben lesz oldalirányú gyorsulása, azaz nem egyenes vonalú pályán fog gördülni. Így viszont elérhető, hogy a forgatóerő éppen a lejtő irányú erővel egyezzen meg, vagyis a golyó egyenes vonalú egyenletes mozgást fog végezni, miközben egyre gyorsabban forog a saját vízszintes tengelye körül is. Ha már ezt beláttuk, akkor viszonylag egyszerűen felírhatjuk a legfontosabb összefüggésegeket, amelyekből a forgó tányér szögsebessége és dőlésszöge függvényében kifejezhető az elgurítás sebessége.

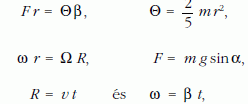
amiből

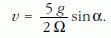
A második feladatban viszonylag egyszerű a két oldalra külön-külön felírható leképezési törvény meghatározása - kis szögek esetén érvényes közelítésben.

Az első leképezésnél

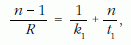
a második leképezésnél pedig

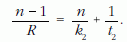
Továbbá az első leképezés képtávolságának és a második leképezés tárgytávolságának összege az üvegrúd hossza, azaz

t1+k2 = 10 cm.

A második tárgytávolság és az első képtávolság hányadosa a tárgytávolság függvényében a következő ábrán látható.

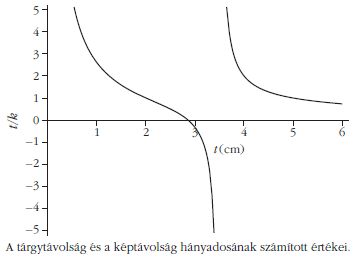
Érdekes volt hallgatni az "öregek" megjegyzéseit, különösen a második és a harmadik feladat megoldásával kapcsolatban. Izgalmas volt azon lehetőség felvetése, hogy az optikai feladat két-két megoldása mellett lehetséges-e további olyan megoldás, amelyben a fény az üvegrúd felületéről - kétszer, vagy akár többször is - visszaverődik.

A harmadik feladatnál a kölcsönös indukciós együtthatót kellett (volna) meghatározni. Ennek két komponense van:

1. ) a gerjesztő toroid "középvonalában" folyó áram feszültséget indukál a második toroidra csévélt menetekben, ennek értéke N2-vel arányos, valamint
2. ) a gerjesztő toroid menetei feszültséget indukálnak a második toroid "középvonalába" képzelt vezetékben, aminek értéke N1-gyel lesz arányos.

   Az alaktényezők a két esetben a szimmetria miatt azonosak. A teljes indukált feszültség a két hatás összege vagy különbsége a tekercselés irányától függően.

   A 2012. évi Eötvös-versenyen összesen 111 dolgozat született, ezek közül 56-ot írtak Budapesten, 55-öt vidéki (összesen 14) helyszínen.

   Első díjat a versenybizottság (elnöke Radnai Gyula, tagjai Honyek Gyula és Vigh Máté) nem adott ki, mert a verseny hagyományai szerint csak az a versenyző kaphat első díjat, aki mindhárom feladatot jól megoldja.

   II. díjat ketten értek el: Janzer Barnabás, a Budapest Fazekas Mihály Gimnázium, 10. osztályos tanulója, felkészítő tanára Horváth Gábor. Szabó Attila, a pécsi Leőwey Klára Gimnázium 12. osztályos tanulója, felkészítő tanárai Simon Péter és Kotek László.

   III. díjat hárman vehettek át: Csősz Gábor, a kecskeméti Református Gimnázium 12. osztályos tanulója, felkészítő tanára Galambos Péter. Juhász Péter, a budapesti Piarista Gimnázium 11. osztályos tanulója, felkészítő tanára Urbán János. Laczkó Zoltán, az ELTE hallgatója, aki a szegedi Ságvári Endre Gimnáziumban érettségizett, mint Győri István tanítványa.

   

   Dicséretben heten részesültek: Béres Bertold (BME, budapesti Puskás Tivadar Távközlési Technikum, Beregszászi Zoltán, Alapiné Ecseri Éva); Fehér Zsombor (budapesti Fazekas Mihály Gimnázium 10. osztály, Horváth Gábor); Homonnay Bálint (budapesti Fazekas Mihály Gimnázium 11. osztály, Horváth Gábor); Kovács Péter (BME, budapesti Apáczai Csere János Gimnázium, Pákó Gyula); Olosz Balázs (pécsi Babits Mihály Gimnázium 10. osztály, Koncz Károly ); Öreg Botond (budapesti Fazekas Mihály Gimnázium 10. osztály, Horváth Gábor) és Szigeti Bertalan György (veszprémi Lovassy László Gimnázium 12. osztály, Varga Vince ).

   

   A díjakat Kroó Norbert, az Eötvös Loránd Fizikai Társulat elnöke adta át. A díjazottaknak gratulált Kürti Jenő, a Társulat főtitkára.

   A verseny díjazottjait külön-külön szólították. A tanulók értékes könyveket kaptak az Eötvös Loránd Fizikai Társulat és az Akadémiai Kiadó (Simonyi Károly: A fizika kultúrtörténete), a Typotex Kiadó (Bronstejn-Musiol-Mühlig-Szemengyajev: Matematikai kézikönyv, illetve J. D. Jackson: Klasszikus elektrodinamika), valamint a Nemzeti Tankönyvkiadó (Juhász Árpád: Gleccserek) jóvoltából. Tanáraik a Matfund Alapítvány szakmai és a Vince Kiadó művészeti könyvei közül válogathattak. A kiadóknak a felajánlott könyvekért, valamint a MOL-nak az anyagi támogatásért a Versenybizottság elnöke mondott köszönetet.

   Az esemény utáni beszélgetéshez a Ramasoft Zrt. biztosította a jóízű szendvicseket és az alkoholmentes italokat.

   Mindegyik díjazott korábban is ért már el sikereket különféle hazai vagy nemzetközi tanulmányi versenyeken. Szabó Attila említette, hogy az idei Eötvös-verseny még a Nemzetközi Diákolimpiánál is nehezebbnek bizonyult, hiszen itt nem tudta megoldani mindegyik feladatot. A harmadik feladat mindenkinek nehéznek bizonyult, így talán nem meglepő, hogy a díjazottak fele 10-11. évfolyamos tanuló.

   Az eredményhirdetés végén többen is megemlékeztek Károlyházy Frigyesről, és dicsérték az általa készített versenyfeladatokat. Károlyházy Frigyesről több írás is szól a Fizikai Szemle korábbi számaiban.