MÉRÉSI EREDMÉNYEK KIÉRTÉKELÉSE JÁNOSSY LAJOS SZERINT

Szatmáry Zoltán
BME Nukleáris Technikai Intézet

Jánossy Lajos szerteágazó tudományos tevékenységében fontos terület a mérési eredmények kiértékelése. Erről szól egyik kézikönyve [1], amelyet már megjelenésének évében lefordítottak oroszra. Később megjelent a magyar kiadása is némileg szűkített, némileg bővített tartalommal. A könyvet számos ország kutatói forgatták és alkalmazták saját méréseik kiértékelésére – többnyire eredményesen. Emlékezetes számomra, amikor egy reaktorfizikai tárgyú, nemzetközi nyári iskola kávészünetében jugoszláv résztvevők a szememre hányták, hogy beprogramozták Jánossy képleteit, de az iteráció sehogyan sem "akart" konvergálni. Ez egy évvel a könyv megjelenése után, tehát 1966-ban történt. A magyar valószínűségelméleti iskola hírneve alapján a beszélgetés résztvevői természetesnek vették, hogy egy magyarnak betéve kellene ismernie nemcsak Jánossy könyvét, hanem a többi világhírű matematikus (Rényi, Prékopa stb.) munkásságát is. Akkor még túlságosan fiatal voltam ahhoz, hogy erre a szemrehányásra megadjam a "helyes" választ. Én ugyanis azt válaszoltam, hogy feltehetően rosszul programozták be a képleteket, ami igaz lehetett, de ma úgy látom: másról volt szó. Később ugyanis felismertem, hogy helyesen beprogramozott helyes képletek még nem feltétlenül elégségesek nagy tömegű mérési eredmény kezelésére. A számítógépi alkalmazásoknak saját problémáik vannak, amelyek megoldásához szintén sajátos módszerekre van szükség. Nem sokkal halála előtt tapasztaltam, hogy maga Jánossy is ráérzett minderre: 1978-ban a KFKI egyik igazgatótanácsi ülésén rosszkedvűen megjegyezte, hogy az ő könyve éppen akkor jelent meg, amikor a számítógépek elterjedtek, így ő már nem terjeszthette ki munkásságát a számítógépek használatára. Az igazgatótanács akkori elnöke (Pál Lénárd) megnyugtatta, hogy a "Jánossy-iskola" létezik és éppen ebbe az irányba fejlődik, nézze meg például az én dolgozataimat. Örömmel adtam át a reaktorfizikában általánosan használt RFIT program elméletéről akkor már létező dolgozataimat. Azután csak egyszer találkoztam vele, amikor jelezte, hogy olvasásukkal még nem végzett, de rövidesen jelentkezik. Nem sokkal később sajnos elhunyt, és csak remélhetem, hogy munkámat támogatta volna, ha tudtunk volna eszmét cserélni róla.

Ez után a kissé személyes bevezető után nézzük meg tartalmilag, melyek voltak Jánossy legfontosabb gondolatai és eredményei, illetve ezek hogyan élnek tovább napjainkban. A legfontosabb gondolat magától értetődőnek tűnik: a mérések eredményeit a matematikai statisztika tételeinek szabatos alkalmazásával kell kiértékelni, ami elsősorban a konfidenciatartomány megszerkesztésére (köznapi nevén: a hibaszámításra) vonatkozik. Sok laboratóriumot ismerek, ahol ugyanezt a Jánossy által elvárt korrektséggel végzik, de jártam egy világszinten is vezetőnek számító laboratóriumban, ahol így gondolkodtak: "a mérési hibán belül nem egyeznek meg a számított és mért adatok, ezért minden mért adat hibáját megnöveljük 1%-kal". Így azután egyezés lett, de akkor minek mértünk? – ezt már én teszem hozzá. Sajnos a mérési adatok kiértékelése olyannak tűnik, mint a labdarúgás vagy a gyermeknevelés: sokan azt képzelik, hogy eleve értenek hozzá. Jánossy könyve ennek csattanós cáfolata: minden, általa vizsgált probléma esetében kellő figyelmet fordít a szórások, illetve a kovarianciamátrix becslésére.

Az ismeretlen paraméterek becslésére konzekvensen a maximum likelihood módszert alkalmazta. Maga a módszer hosszú fejlődés eredménye. A témakörben kevéssé járatos olvasóink számára talán nem lesz haszontalan, ha röviden összefoglaljuk a történelmi fejlődést. Abban az értelemben, ahogy azt ma értjük, a 18. század végén merültek fel méréskiértékelési problémák. Nevezetes P. S. Laplace számítása (1786), amellyel a Föld alakját meghatározta. Már akkor tudták, hogy a Föld nem gömb alakú, hanem egy forgási ellipszoiddal közelíthető. Az ellipszoid paramétereit méréssel határozták meg. Tekintsük az 1. ábrát! A Föld keresztmetszetét mutatja (erősen torzítva), amely a feltevés szerint ellipszis. Különböző földrajzi helyeken megmérték a délkör 1° középponti szöghöz tartozó darabjának M hosszát. A mérés helyét az l szélességi körrel jellemezték. Geometriai megfontolásokkal levezette, hogy M és l között a

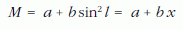
összefüggés áll fenn, ahol a és b az ellipszis alakjától függő ismeretlen állandók. (a és b nem az ellipszis féltengelyeinek a hossza, de azokkal ismert összefüggésben áll. Ha tehát meghatározzuk a-t és b-t, a féltengelyeket is kiszámítjuk.)

A mérési eredmények az 1. táblázatban találhatók. Az eredeti jelöléseket és egységeket az érdekesség kedvéért hagytuk meg: a hosszúságot "dupla öl" egységekben, a szögeket olyan fokban mérték, amely szerint a teljes szög 400°. Laplace a következőképpen okoskodott. Tekintve, hogy nem lehet a és b értékét úgy megválasztani, hogy a képlet minden mérésre pontosan érvényes legyen, a képlet hibáját a lehető legkisebb értékre próbálta leszorítani. Adott a és b mellett meghatározta az

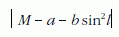
hibatagok maximumát, majd megkereste a és b olyan értékeit, amelyek mellett ez a maximum a legkisebb. A modern terminológia szerint ezt minimax becslésnek nevezzük. Laplace eredménye a következő volt:

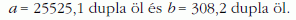
Laplace-nak még ad hoc módszereket kellett alkalmaznia, de Neumann János játékelméletében napjainkra már közismert módszereket dolgoztak ki a minimax problémák megoldására.

Eredetileg A. M. Legendre javasolta a legkisebb négyzetek módszerét (1806). Javaslatát az 1. táblázatban szereplő adatokra vonatkozóan fogalmazzuk meg. Ha az egyes mérések megkülönböztetésére bevezetjük az i indexet, akkor szerinte a

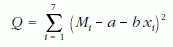
négyzetösszeg minimumát kell keresni. C. F. Gauss – többek között – csillagászati és geodéziai megfigyelések kiértékelésével foglalkozott. 1809-ben ő vetette meg a legkisebb négyzetek módszerének az alapjait. A mai napig használjuk az általa bevezetett fogalmakat és jelöléseket.

A 19. század végén már alkalmazták az úgynevezett L₁-normában vett minimális eltérések módszerét, amely szerint a

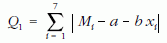
összeg minimumát keressük az a és b paraméterek függvényében. A felmerülő matematikai nehézségek miatt a legkisebb négyzetek módszere, de főleg a maximum likelihood módszer (lásd alább) háttérbe szorította ezt a módszert. Időközben a gazdasági optimalizálás céljaira kifejlődött a lineáris programozás (szimplex módszer), amelyre matematikai szempontból visszavezethető az L₁-norma minimalizálása. Miután erre közhasznú programok jelentek meg, a matematikusok újra ajánlják ennek használatát is, ugyanis a módszernek jelentős előnyei vannak.

Döntő áttörést eredményezett A. Fisher munkássága a 20. század tízes éveiben. Az ő nevéhez fűződik a ma általánosan alkalmazott maximum likelihood módszer. Eszerint a keresett paraméterek becsült értékét úgy választjuk meg, hogy azok mellett a kapott kísérleti eredmények a legvalószínűbbek legyenek. A módszer előnye, hogy matematikailag jól kezelhető formulákra vezet, továbbá hogy a becslésnek kedvező matematikai statisztikai tulajdonságai vannak. Legfontosabb tulajdonságát a paraméterek becslésében alapvető Cramér–Rao-egyenlőtlenség segítségével tudjuk megvilágítani: reguláris becslési problémák (lásd alább) esetében a becsült paraméterek szórása nem lehet egy alsó határnál kisebb, bármilyen módszert használunk is a becslési probléma megoldására. Nos, bebizonyították, hogy a maximum likelihood becslések szórása az alsó határhoz tart, amikor a mérési adatok száma minden határon túl nő. Vannak esetek, amelyekben a szórások már véges számú adatok esetén is minimálisak.

Ezen a ponton visszatérünk Jánossyhoz. Mivel sokat foglalkozott kozmikus sugárzással és elemi részekkel, könyvének példái ilyen jellegűek: a részecskéknek fotoemulzió segítségével való megfigyelésével és a részecskeszámlálással kapcsolatosak. Ha a mérési eredmények Gauss-eloszlásúak, a maximum likelihood módszer átmegy a legkisebb négyzetek Gauss óta bevett módszerébe, de az említett mérések esetében inkább a Poisson-eloszlás az érvényes, tehát nem volt más választása, mint a maximum likelihood módszer.¹ A dolgot egy konkrét mérés példáján mutatjuk be részletesen. Tegyük fel, hogy egy részecskedetektorral egy radioaktív anyagban történő bomlások számát mérjük a t idő függvényében. A t_i időpontban T_i idő alatt mért beütésszám legyen N_i, amelynek várható értéke

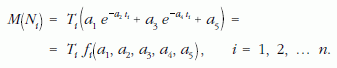
Itt feltettük, hogy a vizsgált anyag két radioaktív izotópot tartalmaz, amelyek bomlási állandója a₂ és a₄; az egyes izotópok mennyisége az a₁ és a₃ paraméterekkel arányos; végül az a₅ paraméter a mérőlaboratórium háttere. Az f_i függvényt illesztőfüggvénynek nevezzük, és az időegységre vonatkozó beütésszám várható értékét adja meg a t_i időpontban. A maximum likelihood módszer szerint fel kell írnunk annak valószínűségét, hogy ebben a mérésben az N₁, N₂, … N_n beütésszám-együttest kapjuk eredményül. A Poisson-eloszlás szerint az i-edik mérésben

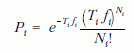
valószínűséggel kapjuk az N_i beütésszámot. Mivel az egyes mérések egymástól függetlenek, az együttes valószínűség ezek szorzata:

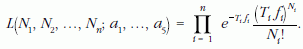
Ezt a függvényt likelihood-függvénynek nevezzük (erre utal az L jelölés). A maximum likelihood módszer értelmében az ismeretlen paramétereket úgy kell megválasztani, hogy L maximális legyen. Matematikailag ez azt jelenti, hogy meg kell oldani a

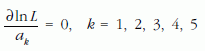
egyenletrendszert.

Mivel transzcendens egyenleteket kaptunk, megoldásuk csak numerikus módszerekkel képzelhető el. Mint a legtöbb kísérleti fizikus, Jánossy is többször írt fel ehhez hasonló egyenletrendszereket (persze más illesztőfüggvényekkel), sőt megoldásukra javasolt iterációs eljárásokat is. Mivel itt már csak számítógépek használata képzelhető el, az iterációk hatékonyságát – mint már megbeszéltük – nem tudta vizsgálni. A fent választott ötparaméteres illesztőfüggvény olyasmi lehet, amellyel fent említett jugoszláv kollégáim próbálkoztak. Nos, az ehhez hasonló függvények a kísérleti fizikusok rémálmai közé tartoznak. Ez különösen akkor igaz, amikor az a₂ és a₄ paraméterek alig különböznek egymástól. Ilyenkor ugyanis a konvergenciát csak nagyon szerencsésen megválasztott kezdőértékkel sikerül elérni. Miután az iteráció konvergált, becslést kapunk a keresett paraméterekre, de ezzel párhuzamosan becsülnünk kell a kapott paraméterbecslések szórását is, mivel ez határozza meg a végeredmény statisztikai bizonytalanságát.

A kezdőértékek megválasztása csak az egyik numerikus probléma, a számítógépi programban tanácsos az iterációt stabilizálni. A számítógépek használatának vannak más következményei is. Ha ugyanis számítógépet használunk, jelentősen megnő a kiértékelhető adatok mennyisége – különösen a korszerű számítógépek teljesítménye mellett. Például a nehéz atommagok ütközésekor egyetlen esemény mintegy 20 Mbyte adatot eredményez, amelyeket µs-ok alatt kell eltárolni. Ilyen feltételek mellett a kísérletező általában nem is látja a primer adatokat, legfeljebb a kiértékelés végeredményét ismeri meg. Ha elég körültekintő, készíttet a szoftverével néhány grafikont, de ez nem változtat azon, hogy a fizikai alapfeltevések (például az illesztőfüggvény) helyességének vizsgálata, a kiszóró adatok kiszűrése és hasonló feladatok fejlett statisztikai módszerek kidolgozását igénylik. Jánossy idejében ezek másképpen merültek fel, mint manapság.

A paraméterek becslésének szabatos végrehajtásán túlmenően Jánossy egy további kérdéssel is foglalkozott. Bár a maximum likelihood módszer önmagában biztosítja, hogy a becsült paraméterek szórása a lehető legkisebb legyen, jogos felvetni azt a kérdést, lehet- e a mérések körülményeinek alkalmas megválasztásával a Cramér–Rao szerinti alsó határt csökkenteni. Ez a kísérletek tervezésének problémája, amellyel Jánossyn kívül számos szerző foglalkozik. Ennek ellenére ezen a területen átütő eredményről még nem sikerült olvasnom.

Befejezésül még két példát hozunk, amelyek jól illusztrálják Jánossy gondolkodását. Az egyik az [1] kézikönyv magyar változatában található, a másikat személyesen tőle hallottam. A részecskeszámlálásban óhatatlan fellép a holtidő: egy részecske megszámlálása után a számlálóberendezés egy τ ideig nem tud további részecskéket megszámlálni. A holtidő hatását az alábbi példával világítjuk meg. Ha T_i idő alatt N_i részecskét regisztráltunk, akkor a számlálóberendezés N_iτ ideig "halott" volt, tehát az effektív számlálási idő

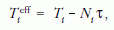
vagyis holtidő nélkül

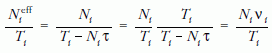
részecskét számláltunk volna meg időegység alatt. Az itt szereplő υi tényező a holtidő-korrekciós tényező, amelyet gyakran alkalmazunk a nukleáris mérések gyakorlatában.² Nem triviális, de be lehet látni, hogy sem N_i, sem 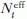nem követi a Poisson-eloszlást, ha i nem eloszlásuk valami más. Amíg tehát nem számítjuk ki ezt az eloszlást, nem alkalmazhatjuk a maximum likelihood módszert, legfeljebb a legkisebb négyzetek módszerének valamilyen közelítő változatára vagyunk utalva. Jánossy vezette le, hogy N_i eloszlása

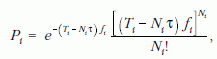
ami lehetővé teszi a maximum likelihood módszer korrekt alkalmazását. A tapasztalat mutatja, hogy a holtidő okozta számlálási veszteségek drámaian tudják befolyásolni az a₂ és a₄ paraméterek becsült értékét – ha a fenti példa mellett maradunk. Nem mindegy tehát, hogyan vesszük figyelembe ezeket a veszteségeket: a Jánossy szerinti korrekt módon vagy a holtidő-korrekciós tényező alapján valamilyen heurisztikus módszerrel.

A másik példánk az elemi részek megfigyelésére vonatkozik. Tegyük fel, hogy valamilyen részecske impulzusát szeretnénk megmérni, de a detektorban (fotoemulzióban, ködkamrában stb.) kapott nyomnak csak egy síkra való vetületét tudjuk megfigyelni.³ Mivel a részecske impulzusának irány szerinti eloszlása izotróp, az i-edik megfigyelt részecske p_i vetülete egyenletes eloszlású a [0, p] intervallumban, ahol p a részecske keresett impulzusa. Mindenek előtt tisztázzuk, hogy ezen mérés kiértékelése nem reguláris becslési probléma. Regulárisnak ugyanis azokat a méréseket nevezzük, amelyek likelihood-függvénye a mért mennyiségeknek olyan halmazán különbözik zérustól, amely független a becsült paraméterektől. Az adott esetben a p_i vetület likelihood-függvénye csak a [0, p] intervallumban különbözik zérustól, azon kívül viszont zérus. Mivel itt éppen a p mennyiséget kívánjuk becsülni, a probléma nem reguláris. Ha ezt figyelmen kívül hagyjuk, p becslésére a reguláris problémáknál megszokott átlagot használjuk:

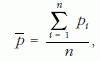
ami reguláris becslések esetében fel szokott merülni. Segítségével a 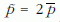becslést kapjuk, amelynek várható értéke p. Meg lehet mutatni, hogy szórása p(3n)^-1/2. Itt visszakaptuk a reguláris becsléseknél megszokott eredményt: a becsült paraméter szórása n^-1/2 rendben tart zérushoz. Mivel azonban a probléma nem reguláris, esetleg ennél lényegesen jobb becslést is lehet találni. Vegyük ezért a mért vetületek közül a legnagyobbat: p_max. Meg lehet mutatni, hogy várható értéke

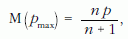
vagyis

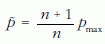
a p mennyiség torzítatlan becslése.

Szórására a

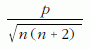
eredményt kapjuk. Elég nagy n-re tehát a szórás 1/n rendben tart zérushoz, ami lényegesen gyorsabb, mint az átlagon alapuló becslés esetében.

Levonhatjuk tehát azt a következtetést, hogy nem árt a likelihood-függvény természetét alaposan megvizsgálni, mielőtt mérési eredményeink kiértékelésébe fognánk.

Irodalom

____________________

1. Csak mellékesen jegyezzük meg, hogy ebben az esetben a maximum likelihood módszer egyenletei matematikailag ugyanolyan alakúak, mint a legkisebb négyzetek módszerének egyenletei, tehát mindkét módszer esetében ugyanazt a számítógépi programot alkalmazhatjuk. Mindez persze nem kisebbíti Jánossy érdemeit, aki – mint már említettük – nem ment el a számítógépi megvalósításig.
2. τ értéke Jánossy idejében 100 µs nagyságrendű volt, ami korunkban a µs-os tartományba csökkent. Így vagy úgy, de a kísérleti fizikusok hajlamosak túlfeszíteni a húrt: υ_i jellegzetes értéke 1,05–1,10.
3. A modern kísérleti technikával az impulzus mindhárom komponensét meg tudjuk mérni. Így az alábbiaknak csak módszertani jelentőségük van.