Fizikai Szemle honlap |
Tartalomjegyzék |
Völgyesi Lajos
BME Általános- és Felsőgeodézia Tanszék
A Föld bonyolult forgási jelenségeinek megismeréséhez pontos fizikai alapismeretek szükségesek. A fogalmak nem egységes és hibás használata, valamint a precesszió és a nutáció jelenségének összekeveredése szükségessé teszi az alapfogalmak tisztázását [1]. A súlyos és az erőmentes pörgettyűk precessziós és nutációs mozgásának áttekintését követően a Föld forgásának részletes tanulmányozásával foglalkozunk, és javasoljuk a szaknyelvben széleskörűen elterjedt hibás elnevezések helyett újak, például a csillagászati nutáció helyett a precessziózavar fogalmának használatát. Ebben az írásban a Föld precessziós mozgásával, a rákövetkezőben pedig a pólusmozgással, vagyis a Föld nutációs mozgásával foglalkozunk.
A Föld saját tengelye körüli forgását az ω forgási szögsebességvektora jellemzi, ezért forgásának leírásához ismernünk kell a szögsebességvektor térbeli irányát és nagyságát, valamint a forgástengely és a Föld tömegének relatív helyzetét, mint az idő függvényét.
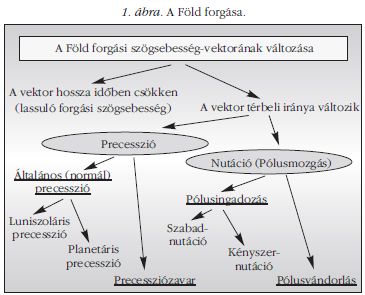
A tengelykörüli forgás során a szögsebességvektor térbeli iránya és nagysága is állandóan változik. A változásokat az 1. ábrán összefoglalva láthatjuk. A szögsebességvektor abszolút értékének (illetve a napok hosszának) változásaival most nem foglalkoztunk; csupán megjegyezzük, hogy a forgási szögsebesség szekuláris lassulása elsősorban a Hold és a Nap által okozott úgynevezett dagálysúrlódás következménye, az évszakos változást alapvetően felszíni (meteorológiai) tényezők, a rendszertelen változásokat pedig a Föld tömegátrendeződései okozzák.
A szögsebességvektor térbeli irányának változásai két csoportra oszthatók: a precessziós és a nutációs mozgásra. A nutációs mozgást a földtudományokban célszerűbben pólusmozgásnak nevezik.
Pörgettyűnek nevezzük minden olyan tetszőleges alakú és tömegeloszlású merev testet, amely egyetlen rögzített pontja körül szabadon foroghat. Általánosabban pörgettyűnek nevezzük a rögzített pont nélküli testet akkor is, ha a tömegközéppontja körüli forgása a tömegközéppont mozgásától függetlenül tárgyalható. Két alapvetően fontos fajtája a 2. ábrán látható úgynevezett súlyos és az erőmentes pörgettyű. A súlyos pörgettyű a súlypontjára ható forgatónyomaték hatására megfelelő ω forgási szögsebesség esetén precessziós mozgást végez, azaz a forgástengely a testtel együtt kúppalást mentén ωpr >> ω szögsebességgel körbevándorol. Az erőmentes pörgettyű ettől abban különbözik, hogy a külső erőknek a súlypontjára vonatkozó forgatónyomatéka zérus (ilyen például a súlypontjában alátámasztott pörgettyű). Az erőmentes pörgettyű nutációs mozgást végez, amennyiben a test nem pontosan a szimmetriatengelye körül forog. Ekkor a test forgástengelye folyamatosan változtatja a testhez viszonyított helyzetét: a forgástengely a test szimmetriatengelye körül kúppalást mentén körbevándorol. Az erőmentes pörgettyű értelemszerűen precessziós mozgást nem tud végezni, viszont a súlyos pörgettyű a precessziós mozgása mellett nutációs mozgást is végezhet, amennyiben nem pontosan a szimmetriatengelye körül forog.
A súlyos és az erőmentes pörgettyűk különböző fajtái léteznek a tömegeloszlásuk, azaz a tehetetlenséginyomaték-tenzoruk főátlójában lévő A, B és C főtehetetlenségi nyomatékok függvényében. Például az A= B ≠ C (homogén forgásszimmetrikus testek) esetén szimmetrikus pörgettyűről beszélünk.
Minden merev test forgása során a forgási tehetetlensége miatt igyekszik megtartani forgási állapotát, más szóval az impulzusnyomaték megmaradási törvénye értelmében bármely zárt rendszer N impulzusnyomatéka állandó, tehát dN/dt időbeli változása zérus.
Ha a forgó merev testre külső erők hatnak, akkor az impulzusnyomaték megváltozása a külső erők M forgatónyomatékával egyenlő:

A forgatónyomaték vektora az F erő és az r erőkar vektoriális szorzata:

az impulzusnyomaték pedig:

ahol I a merev test tehetetlenséginyomaték-tenzora, ω pedig a forgási szögsebesség vektora. Behelyettesítve a (2) és a (3) összefüggést az (1)-be:
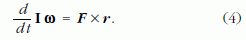
Mivel merev test esetén I állandó, ezért az I kiemelhető a differenciálási jel elé, tehát (4) az
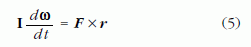
formában is írható. Ebből viszont már közvetlenül látható, hogy külső forgatónyomaték hatására a nehézségi erőtérben megfelelően gyorsan forgó merev testek (az úgynevezett súlyos pörgettyűk) ω szögsebességvektorának térbeli iránya folyamatosan változik; az ω vektor mindenkor az F és az r irányára merőleges irányban mozdul el. Ennek megfelelően a 3. ábrán látható ferde tengelyű, gyorsan forgó pörgettyű (például a mindenki által jól ismert játék: a búgócsiga) nem dől el, hanem forgástengelye a test tömegével együtt függőleges tengelyű körkúp palástja mentén állandó ωpr >> ω precessziós szögsebességgel lassan körbevándorol. A pörgettyű forgástengelyének ezt a mozgását precessziós mozgásnak nevezzük.
Ettől teljesen független az erőmentes (forgatónyomaték nélküli, súlypontjában alátámasztott) szimmetrikus pörgettyűk nutációs mozgása. A precesszióval ellentétben a nutáció során a test forgástengelye a szimmetriatengely körüli kúppalást mentén egyenletes sebességgel körbevándorol, amennyiben a forgás- és a szimmetriatengely nem esik egybe [2, 3].
Földünk forgástengelye a külső erők hatására a fentiekben tárgyalt súlyos pörgettyű mozgásához teljesen hasonló mozgást végez, a különbség mindössze annyi, hogy a Föld esetében az ωpr vektor iránya (a forgástengely körbevándorlásának iránya) ellentétes. Ennek oka az, hogy a 3. ábrán látható pörgettyűre olyan irányú forgatónyomaték hat, ami a forgástengelyét fekvő helyzetbe igyekszik hozni; a Föld esetében viszont a Nap és a Hold egyenlítői tömegtöbbletre gyakorolt vonzása olyan erőpárt hoz létre, amely a Föld forgástengelyének irányát az ekliptika síkjára merőlegesen felállítani igyekszik.
Vizsgáljuk meg részletesebben a Föld precessziós mozgását és ennek okát. A Föld jó közelítéssel forgási ellipszoid alakú, amelynek egyenlítői sugara (fél nagytengelyének hossza) mintegy 21 km-rel nagyobb a sarkok felé mérhető távolságnál (a fél kistengelyének hosszánál). Ugyanakkor a Föld egyenlítői síkja mintegy 23,5 fokkal hajlik a Föld keringési síkjához (az ekliptika síkjához), amelyben a Nap, és amelynek közelében a Hold és a bolygók találhatók. Az egyszerűség kedvéért egyelőre csupán a Nap tömegvonzásából adódó forgatónyomaték hatását vizsgáljuk meg. A Föld lényegében a Nap tömegvonzási erőterében végzi keringését és dinamikus egyensúlyban van; vagyis a Nap Föld tömegközéppontjára ható F0 tömegvonzásával a Föld Nap körüli keringéséből származó (az F0 erővel egyenlő nagyságú, de ellentétes irányú) -FK keringési centrifugális erő tart egyensúlyt. Ez a keringési centrifugális erő a Nap-Föld közös tömegközéppontja körüli excentermozgás következtében a Föld minden pontjában azonos irányú és egyenlő nagyságú [4].
A gömbszimmetrikus tömegeloszlástól tapasztalható eltérés miatt osszuk a Földet a 4. ábrán látható belső gömbszimmetrikus tömegtartományra és az egyenlítő menti gyűrűszerű tömegtöbbletre! Legyen a Naphoz közelebb eső gyűrűrész tömegközéppontja P1, a távolabbi részé pedig P2. A Nap Föld gömbszimmetrikus tömegtartományára ható tömegvonzását úgy értelmezhetjük, mintha ez csak a gömb 0 tömegközéppontjában lépne fel. A gyűrűrészekre ható vonzóerőt viszont a P1 és a P2 tömegközéppontban ható vonzóerőkkel helyettesíthetjük. A Newton tömegvonzási törvényének megfelelően a P1-ben nagyobb, a P2-ben pedig kisebb vonzóerő hat, mint a 0 tömegközéppontban. A keringési centrifugális erő viszont mindhárom pontban ugyanakkora [4], ezért a P1-ben és a P2-ben a kétfajta erő nincs egymással egyensúlyban; a P1-ben a vonzóerő, a P2-ben a keringési centrifugális erő a nagyobb. A két erő eredője a P1 pontban: F = F1-FK, a P2 pontban pedig F = FK-F2. Ez a két egyenlő nagyságú, de ellentétes irányú erő a 4. ábra síkjából merőlegesen kifelé mutató M forgatónyomaték- vektort eredményez. A Naphoz hasonlóan a Hold is forgatónyomatékot fejt ki a Földre, sőt a Hold által keltett forgatónyomaték a Hold közelsége miatt jóval nagyobb. Az ily módon keletkező forgatónyomatékok együttes hatásának eredménye a Föld 4. ábrán bemutatott precessziós mozgása: az úgynevezett luniszoláris precesszió.
A luniszoláris precesszió során a Föld forgástengelye, az ekliptika és az égi egyenlítő síkja 23,5°-os hajlásszögének megfelelően, 2×23,5° = 47°-os nyílásszögű kúp palástja mentén mozog úgy, hogy egy teljes körüljárást közel 25 730 év alatt végez. Ez a 4. ábra tanúsága szerint azt jelenti, hogy a Föld forgástengelyének északi iránya körülbelül 5000 évvel ezelőtt az Alfa Draconis csillag közelébe mutatott, az égi pólus jelenleg az Alfa Ursa Minoris (Polaris) közelében van és körülbelül 5000 év múlva az Alfa Cephei közelében lesz. Így a jelenleg élő generációknak csupán véletlen szerencséje, hogy az égi északi pólus helyéhez közel viszonylag fényes csillag, a Sarkcsillag található.
Mivel a Naprendszer bolygói nem az ekliptika síkjában keringenek a Nap körül, ezért tömegvonzási hatásukra a Föld keringési síkja állandóan lassú ingadozásban van a bolygók közepes pályasíkjához képest. Emiatt az ekliptika síkjának és az égi egyenlítő síkjának hajlásszöge közel 40 000 éves periódussal körülbelül 22° és 24,5° között ingadozik, vagyis az ekliptika normálisa közel 40 000 éves periódussal körbevándorol egy körülbelül 2,5 fokos nyílásszögű körkúp palástja mentén (5. ábra). Mivel így folyamatosan változik az ekliptika pólusának helyzete, az égi pólus mozgását ehhez viszonyítva, az ekliptika pólusának mozgását is a forgástengely precessziós mozgásaként észleljük. A jelenséget planetáris precessziónak nevezzük.
A planetáris precessziót tehát az ekliptika síkjának billegése okozza. Az ekliptika pólusának ezzel a mozgásával 40 000 éves periódussal hol kissé szétnyílik, hol kissé összezáródik a precessziós kúp nyílásszöge, ily módon a luniszoláris precessziós kúp nyílásszöge nem stabilan 47 fok, hanem közel 40 000 éves periódussal körülbelül 2×22°= 44° és 2×24,5° = 49° között ingadozik.
Valójában az történik, hogy az ekliptika síkjának mozgása miatt 40 000 éves periódussal folyamatosan más-más irányban látható a Földről a Nap és a Hold, és így az 5. ábra tanúsága szerint változik a P1 és a P2 rész-tömegközéppontok távolsága az ekliptika síkjától. Ezzel pedig - mivel változik az erő karja - folyamatosan változik (ingadozik) a precessziós mozgást előidéző forgatónyomaték
A luniszoláris és a planetáris precessziós mozgás eredője az általános precesszió, más néven a normálprecesszió. A normálprecessziós mozgás során az ekliptika pólusának változása miatt az égi pólus nem pontosan a 4. ábra felső részén látható körpálya mentén mozdul el, hanem az állócsillagokhoz viszonyítva a körpályát közelítő, de valójában önmagában nem záródó görbe mentén vándorol, és egy teljes körüljárás ideje is kissé megnő, közel 25 786 évre.
A Hold, a Nap és a bolygók Földhöz viszonyított relatív helyzetváltozásai következtében a Földre időben változó forgatónyomaték hat, ezért a normálprecessziós mozgásra különböző rövidebb periódusú ingadozások rakódnak. A forgástengely precessziós mozgásának ezen rövidperiódusú változásait sokan helytelenül csillagászati nutációnak nevezik. Valójában ennek semmi köze a nutációhoz, csupán formailag megtévesztően hasonlít egy nutációs mozgás rövidebb hullámaihoz. Célszerű ezért ezt a jelenséget inkább precessziózavarnak nevezni.
A precessziózavar több különböző periódusú és amplitúdójú mozgásból tevődik össze és rakódik rá a hosszúperiódusú (szekuláris) precessziós mozgásra. A Nap és a Föld egymáshoz viszonyított helyzetváltozásai miatt két fontosabb periódusa van. A Nap által a Föld egyenlítői tömegtöbbletére kifejtett forgatónyomaték nagysága a Nap deklinációjának szögétől (a Föld egyenlítő síkja feletti magasságától) függ. A 4. ábra például a téli napforduló helyzetében ábrázolja a Földet, amikor δ = -23,5°. Ekkor és a nyári napforduló napján (amikor δ = +23,5°) a Nap maximális forgatónyomatékot fejt ki a Földre. A két helyzet között csökken, illetve növekszik a forgatónyomaték. A tavaszi és az őszi napéjegyenlőség pillanatában a Föld két egyenlítői tömegtöbbletének 4. ábrán értelmezett P1 és P2 súlypontja azonos távolságra van a Naptól, ekkor tehát a precessziót okozó forgatónyomaték nulla. Ennek megfelelően, a Nap deklinációjának változása miatt, fél éves periódussal változik a Föld precessziós mozgása. Ehhez egy éves periódusú precessziós változás is járul, ami annak következménye, hogy a Föld ellipszis alakú pályán kering a Nap körül és ezáltal egy éves periódussal változik a Naptól mért távolsága, illetve ennek megfelelően a forgatónyomaték.
Többek között teljesen hasonló jellegű, de rövidebb periódusú és nagyobb amplitúdójú változásokat okoz a Hold a Föld körüli keringése során. A Hold a Föld körüli pályáját közel 28 nap alatt futja be, ezért a Hold deklinációjának változása miatt adódó precessziós periódus körülbelül 14 napos, az ellipszispályán történő keringés miatti változó Föld-Hold-távolságból származó periódus pedig 28 napos.
A Hold mozgásának azonban ezeknél jóval markánsabb hatása is van. Ez annak a következménye, hogy a Hold más síkban kering a Föld körül, mint amelyben a Föld kering a Nap körül. A Hold pályasíkja közel 5° 09' szöget zár be az ekliptika síkjával, a Hold pályasíkjának az ekliptika síkjával alkotott metszésvonala (a holdpálya csomóvonala) pedig az ekliptika síkjában 18,6 éves periódussal hátráló irányban körbevándorol. Ennek következménye a precesszió szempontjából jól látható a 6. ábrán.
Ennek hatása nagyon hasonlít a planetáris precesszió 5. ábrán bemutatott hatásához. Valójában itt is az történik, hogy a holdpálya síkjának mozgása miatt 18,6 éves periódussal folyamatosan más-más irányban látható a Földről a Hold, és ezzel a 6. ábra tanúsága szerint folyamatosan változik a P1 és a P2 rész-tömegközéppontok távolsága a holdpálya síkjától. Ezzel pedig, mivel folyamatosan változik az erő karja, folyamatosan változik (ingadozik) a precessziós mozgást előidéző forgatónyomaték.
A precessziózavar holdpálya csomóvonala mozgásából származó tagja sokszorosan nagyobb, mint a precessziót alkotó összes többi ingadozás együttesen, ezért ezt a precessziózavar lunáris főtagjának nevezzük.
A Föld forgási szögsebességvektora tehát az ekliptika síkjának a Föld tömegközéppontján átmenő normálisa körül jelenleg körülbelül 47°-os közepes csúcsszöggel a 6. ábrán látható hullámos kúppalást mentén közel 26 000 éves periódussal vándorol körbe. Ennek megfelelően az égi pólusok (az északi és a déli pólus) az ekliptika pólusaitól 23,5° közepes pólustávolságban hullámos körpálya mentén mozognak. A hullámok közül kiemelkedően legnagyobb a precessziózavar lunáris főtagjának 18,6 éves periódusú hulláma. Az ekliptika pólusa körül az égi pólusok által leírt precessziós körön a precessziózavar lunáris főtagjának mintegy 26 000/18,6 ≈ 1400 hulláma van. E hullámok amplitúdója körülbelül 9" (ennyi a forgástengely hajlásának ingadozása: az úgynevezett ferdeségi tag), hullámhossza pedig közel 15,6'.
A precessziós mozgást a precessziózavar főtagjával együttesen szokás a 7. ábrán látható úgynevezett precessziós ellipszissel is szemléltetni. (Nem szerencsés a gyakorlatban eddig elterjedt nutációs ellipszis elnevezés, hiszen ennek a nutációhoz szintén semmi köze.) Eszerint a precessziós ellipszis középpontja az ekliptika pólusa körül 23,5° pólustávolságban egyenletes sebességgel vándorol és tesz meg egy teljes kört közel 26 000 év alatt, miközben a valódi - a pillanatnyi - égi pólus a precessziós ellipszis mentén mozog 18,6 éves periódussal. A precessziós ellipszis 9" távolságú fél nagytengelye mindig az ekliptika pólusa irányába mutat, a 7" távolságú fél kistengelye pedig erre merőleges.
A fentiek alapján világosan látható, hogy a csillagászati nutáció helytelen elnevezés, egyrészt mert nem csillagászati, másrészt pedig nem is nutáció. Elvileg persze bármit bárminek elnevezhetünk, azonban szabadságunk mégsem teljes, mert egyaránt nem szerencsés, például egy kislányt Ádámnak, vagy a precessziót nutációnak nevezni. A Hold, a Nap és a bolygók Földhöz viszonyított relatív helyzetváltozásai miatt az időben változó forgatónyomaték következtében kialakuló rövidebb periódusú ingadozások nem nevezhetők fizikai értelemben nutációnak. Az érintett égitestek bonyolult mozgása miatt ugyanis a precessziót előidéző forgatónyomaték változik, ami következtében a Föld tömege a hozzá képest rögzített helyzetű forgástengelyével együtt végzi a változó precessziós mozgását. Ezzel szemben a nutációs mozgás során a Föld forgástengelye nem együtt mozog a Föld tömegével, hanem bármiféle forgatónyomaték hatásától függetlenül, a Föld tömege, illetve szimmetriatengelye különválva a forgástengelytől végzi a bonyolult sajátmozgását (ami pusztán abból adódik, hogy a forgás nem pontosan a szimmetriatengely körül történik). Egyszerűbben fogalmazva a precessziós mozgásért a Földön kívüli tömegek forgatónyomatéka felelős, a nutációs mozgásban viszont kizárólag a Föld saját tömegének (tömegeloszlásának) a forgástengelyéhez viszonyított helyzete játszik szerepet.
A Föld precessziós mozgása a csillagászati megfigyelések szempontjából abban nyilvánul meg, hogy az égi pólus (a Föld forgástengelye és az éggömb metszéspontja) az ekliptika pólusa körül lassan körbevándorol (8. ábra). Az égi egyenlítő síkja merőleges a Föld forgástengelyére, ezért a forgástengely irányának elmozdulása az égi egyenlítő síkjának elfordulásával is jár. Tehát az ekliptika és az égi egyenlítő síkjának metszésvonalában levő γ tavaszpont is elmozdul az ekliptika mentén, ami viszont a csillagászatban használatos ekvatoriális (égi egyenlítői) koordinátarendszer kiinduló iránya. Így a normálprecesszió és a precessziózavar az égitestek égi egyenlítői koordinátáinak (α rektaszcenziójának és δ deklinációjának) folyamatos változását okozzák.
A Föld tömege a forgástengelyével együtt végzi a leírt precessziós mozgásokat, ezért a földfelszíni pontok forgástengelyhez viszonyított földrajzi koordinátái a precessziós mozgástól függetlenek. Így a földi koordináták, a szintfelületi földrajzi szélesség- és hosszúságértékek a normálprecesszió és a precessziózavar hatására nem változnak.
A Föld nutációs mozgásával (a pólusmozgással) a következő cikkben foglalkozunk.