
Fizikai Szemle honlap |
Tartalomjegyzék |
Völgyesi Lajos
BME Általános- és Felsogeodéziai Tanszék
Földünk tengely körüli forgása nehezen átlátható, meglehetősen bonyolult folyamat. Az előző [1] cikkben áttekintettük a legfontosabb fizikai alapfogalmakat, a súlyos és az erőmentes pörgettyű precessziós és nutációs mozgását és részletesen foglalkoztunk a Föld precessziós mozgásával. Ebben az írásban a Föld nutációs mozgásával (pólusmozgás, pólusingadozás, pólusvándorlás, szabadnutáció, kényszernutáció jelenségeivel) foglalkozunk.
Ha forgó merev testre külső erők hatnak, akkor az impulzusnyomaték megváltozása a külső erők M forgatónyomatékával egyenlő, így az ω szögsebességgel forgó merev test kinetikai egyensúlyának feltétele külső (a testtel nem együttforgó) K'(x', y ',z ') inerciarendszerből szemlélve:

Térjünk át az 1. ábrán látható K'(x', y ',z ') inerciarendszerről a merev testtel együtt forgó K(x, y,z) koordináta-rendszerre. Ha a forgó K koordináta-rendszeren belül az N vektor nem változna, akkor a K' inerciarendszerből szemlélve az N vektor változása csak a forgásból állna:
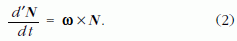
Ha N a K rendszerből szemlélve is változik, akkor:
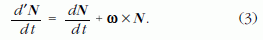
A (3) vektor-transzformációból az (1) felhasználásával:
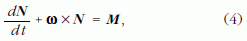
ami a merev testtel együtt forgó megfigyelő számára a forgási egyensúly feltétele (az Euler-féle egyenlet vektoralakban).
Kifejtve a (4) összefüggésben szereplő vektoriális szorzatot az x, y, z koordináta-irányokban az alábbi skaláregyenletekre jutunk:
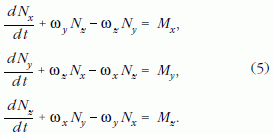
Ha a K koordináta-rendszert a test tömegközéppontjában úgy vesszük fel, hogy az x, y, z tengelye egybeessen a test tehetetlenségi főirányaival, akkor a főátlón kívüli centrifugális nyomatékok zérusok, és a tehetetlenségi nyomaték tenzora
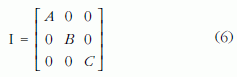
formában írható. Ekkor:
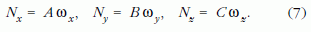
Behelyettesítve az impulzusnyomaték (7) szerinti összetevőit az (5) egyenletekbe, a merev testek forgását leíró Euler-féle mozgásegyenleteket (az úgynevezett pörgettyűegyenleteket) kapjuk, a merev testtel együtt forgó K koordináta-rendszerben:
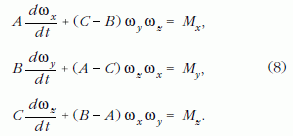
A (8) Euler-féle pörgettyű egyenletek integrálásával meghatározható a forgó testek mozgása, vagyis az ω forgási szögsebességvektor összetevőinek ωx (t), ωy (t ), ωx (t) időbeli változása a testtel együtt forgó koordináta-rendszerben.
További feladat külső szemlélő számára a vizsgált forgó test térbeli helyzetének meghatározása az idő függvényében. Azaz, meg kell adni a merev testtel együtt forgó K(x, y,z) koordináta-rendszer helyzetét a térben rögzített K'(x',y',z') inerciarendszerhez viszonyítva.
A K rendszer K'-höz viszonyított helyzete legegyszerűbben az 1. ábrán szemléltetett θ, Ψ, Φ Euler-féle szögekkel adható meg [2, 3]. A testtel együtt forgó K koordináta-rendszerben az ω szögsebességvektor összetevői az Euler-féle szögekkel a
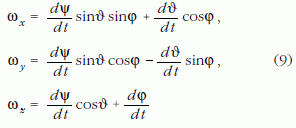
összefüggéssekkel fejezhetők ki [4]. Amennyiben a (8) Euler-féle egyenletekből ismertek az ωx (t ), ωy (t ), ωz (t ) megoldások, akkor a (9) elsőrendű differenciálegyenletekből meghatározhatók a θ(t), Ψ(t), Φ(t) Euler-féle szögek időbeli változásai. A θ, Ψ, Φ szögekre közvetlenül is nyerhető megoldás ha a (9) összefüggéseket a (8) Euler-féle egyenletekbe írjuk. Ekkor három másodrendű differenciálegyenlet adódik, amiből a θ, Ψ, Φ szögek közvetlenül meghatározhatók.
Amennyiben a (8) Euler-féle egyenleteket erőmentes szimmetrikus pörgettyűnek feltételezett merev Földre alkalmazzuk, az alábbi egyszerűsítő feltevéseket tehetjük:
Ezekkel a feltevésekkel a (8) Euler-féle mozgásegyenletek az
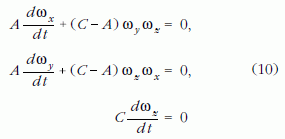
alakra egyszerűsödnek.
Mivel C ≠ 0, a harmadik egyenlet megoldása:

tehát a z tengely körüli forgás szögsebessége állandó, vagyis az ω szögsebességvektor szimmetriatengelyre eső vetülete nem változik. A további megoldásához osszuk el az (10) első két egyenletét A-val, írjuk be ezekbe a (11) megoldást, és vezessük be a

jelöléssel a dinamikai lapultság fogalmát. Ekkor a (10) első két egyenlete
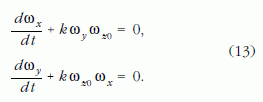
Differenciáljuk a (13) első egyenletét t szerint és helyettesítsük be az így keletkező dωy /dt differenciálhányados kifejezését a (13) második egyenletébe. A rendezés után:
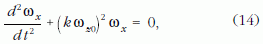
amely másodrendű differenciálegyenletnek az ωx = 0 triviális megoldása mellett az
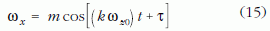
is megoldása, amelyben m és τ integrálási állandók (a harmonikus rezgőmozgás differenciálegyenletének megoldásához hasonlóan m a legnagyobb kitérést, τ pedig a kezdőfázist jelöli).
Hasonlóképpen kapjuk meg az ωy értékét:
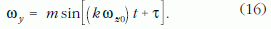
Legyenek a t = 0 időpontban ωx = m és ωy = 0 kezdeti feltételek (vagyis a kezdő időpontnak azt választjuk, amikor az ω vektor éppen az xz síkban fekszik). Ekkor a (15) és a (16) szerint τ = 0.
Bevezetve az

jelölést, a (11), (15) és a (16) alapján az ω forgási szögsebességvektor összetevői:
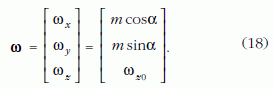
A kapott eredményeket a 2. ábrán szemléltetjük. Eszerint az ω vektor összetevőiben szereplő α nem más, mint a z koordinátatengely és az ω vektor által meghatározott síknak az xz síkkal bezárt szöge. Mivel az α a (17) szerint a t időnek lineáris függvénye, ezért
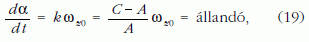
tehát az ω vektor állandó szögsebességgel járja körül a test tömegéhez rögzített koordináta-rendszer z tengelyét.
Az ω (18) összetevőit megvizsgálva látható, hogy az ω vektor végpontja a z tengely körül a (19) szerint állandó szögsebességgel
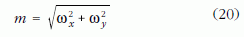
sugarú kört ír le, így maga a forgási szögsebességvektor, vagyis a Föld forgástengelye
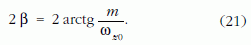
nyílásszögű körkúp palástja mentén mozog a tehetetlenségi főtengellyel azonos z koordináta-tengely körül.
A Föld forgása tehát nem a C szimmetriatengely körül (azaz nem a Föld tömegéhez kötött állandó helyzetű z tengely), hanem mindig a pillanatnyi forgástengely körül történik. A Föld felszínén az ω vektor végpontja által leírt kör (a pillanatnyi forgástengely földfelszíni nyomvonala) a merev Föld póluspályája, vagy pollódiuma.
Határozzuk meg ezek után a pillanatnyi forgástengely egy teljes körülvándorlásának idejét. Jelölje TE azt az időt, amely alatt a forgástengely egyszer körüljárja a z tengelyt. Ekkor a (17) alapján:
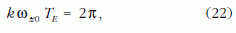
amiből:
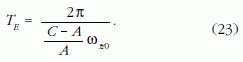
Mivel a forgás jó közelítéssel a z tengely körül történik, ezért ωz0 ≈ |ω| , azaz
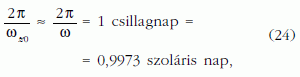
tehát:

Csillagászati megfigyelések szerint:
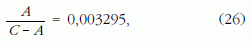
így tehát

Mivel a mozgásegyenletek fenti levezetése Eulertől származik, a forgástengely állandó szögsebességű körbevándorlásának 303 napos periódusát Euler-féle periódusnak (gyakran Euler-féle szabadnutációs periódusnak) nevezzük. Az elnevezésben a "szabad" jelző arra utal, hogy a jelenség külső erőhatásoktól teljesen független és a kialakult mozgás periódusidejét kizárólag a merev test (esetünkben a Föld) tömegeloszlása (lapultsága) határozza meg.
Mindezekből az következik, hogy ha valamely merev test tengelykörüli forgása nem a C fő tehetetlenségi nyomaték tengelye körül indult meg, akkor ez a mozgási állapot megmarad, tehát a forgástengely nem billen vissza olyan állapotba, hogy a fő tehetetlenségi tengellyel egybeessék. Így a pillanatnyi forgástengely állandó szögtávolságra, egyenletes sebességgel járja körül a fő tehetetlenségi tengelyt. Amikor a forgástengely pontosan egybeesik a szimmetriatengellyel (β = 0), vagy az A = B = C esetén a mozgás ugyanolyan, mint egy rögzített tengely körüli állandó szögsebességű forgás, azaz nutáció nem lép fel.
Mindez, amit eddig tárgyaltunk, a Földdel együtt forgó K koordináta-rendszerből szemlélve látható. A következő feladat az Euler-szögek meghatározása, ami lehetővé teszi az erőmentes szimmetrikus pörgettyű nutációs mozgásának leírását külső inerciarendszerből szemlélve.
Induljunk ki a (9) differenciálegyenletekből! Ezeknek elegendő egy partikuláris megoldása, mivel az általános megoldásban szereplő három integrációs állandót a K' koordináta-rendszer szabad választásával automatikusan megadjuk [2]. Vegyük fel a térhez rögzített K' koordináta-rendszerünk z tengelyét az 1. ábrán szemléltetett módon úgy, hogy iránya megegyezzen az (1) miatt a térben állandó helyzetű N impulzusnyomaték-vektor irányával, továbbá tételezzük fel, hogy a z' és a z irányok közötti υ szög az időben nem változik, tehát:
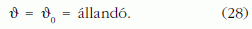
Ekkor behelyettesítve a (9) differenciálegyenletekbe a (11), (15) és a (16) megoldásokat:
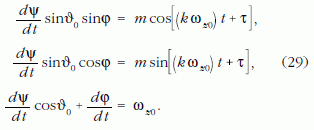
Az első két egyenletből a koordináták 1. ábrán látható értelmezése mellett az alábbi két összefüggés adódik:
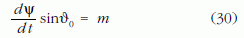
és
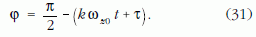
Beírva ezeket a (29) harmadik egyenletébe, kiszámítható a υ0 értéke:
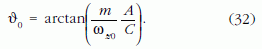
Összefoglalva végül az Euler-szögekre kapott megoldás:
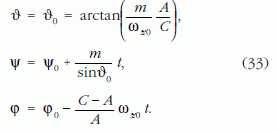
A (33) első két összefüggése azt mutatja, hogy külső inerciarendszerből szemlélve az erőmentes pörgettyű C szimmetriatengelye a térben állandó helyzetű N impulzusnyomaték-vektor körül 2υ0 nyílásszögű úgynevezett nutációs kúp palástja mentén állandó m/sinυ0 szögsebességgel mozog körbe, miközben a harmadik egyenlet szerint ehhez még hozzájön egy további forgás a C szimmetriatengely körül. Az N vektor C szimmetriatengellyel bezárt υ0 szögét a (33) első összefüggése, míg a C szimmetriatengely ω pillanatnyi forgástengellyel bezárt β szögét pedig a (21) összefüggés adja. Ebből viszont az ω pillanatnyi forgástengely N vektorral bezárt γ szöge is meghatározható.
Két alapeset lehetséges: a C > A esetben γ = β - υ0, míg a C < A esetben γ = υ0 - β.
Összefoglalva a fentieket: szabadnutáció esetén a külső térben rögzített K' inerciarendszerben mind a Föld forgástengelyének, mind a Föld C szimmetriatengelyének iránya folyamatosan változik, csupán az N impulzusnyomaték-tengely iránya változatlan, az impulzusnyomaték- megmaradási törvény értelmében. A mozgást legegyszerűbben a 3. ábra alapján érthetjük meg - ami egyébként az erőmentes pörgettyű szabadnutációs mozgását mutatja a külső térben rögzített inerciarendszerből szemlélve. A Föld pillanatnyi forgástengelye (C > A esetén) a kisebb nyílásszögű, úgynevezett herpolhodia kúp palástja mentén, a C szimmetriatengely (a Föld tehetetlenségi főiránya) pedig a nagyobb nyílásszögű úgynevezett nutációs kúp palástja mentén kerüli meg az N impulzusnyomaték-vektort. Eközben az ω vektor az úgynevezett polhodia kúp palástja mentén a C tengely körül is vándorol. A mozgás során az ω, az N és a C mindig egy síkban van, miközben a Föld tömegéhez rögzített helyzetű polhodia kúp és az inerciarendszerben rögzített helyzetű herpolhodia kúp palástja állandóan az ω vektor iránya mentén érintkezve csúszásmentesen gördül egymáson.
A valódi Föld pillanatnyi forgástengelyének fő tehetetlenségi irányát jól közelítő (megállapodással definiált) tengelyéhez viszonyított (mérésekkel meghatározható) mozgását pólusingadozásnak nevezzük. Az eddigi feltevések (például merev és forgásszimmetrikus Föld esete) a valóságban nem érvényesek, ezért a megfigyelt pólusingadozás jelentősen eltér az eddigi megfontolások eredményeitől.
Ha mérésekkel meghatározzuk a valódi póluspályát (a forgástengely mozgásának földfelszíni nyomvonalát) a pollódiumot, akkor folyamatosan a 4. ábra felső részén látható görbékhez hasonló képet kapunk. A 4. ábrán az 1967 és 1979 közötti póluspálya látható olyan koordináta-rendszerben, amelynek +x tengelye a greenwichi kezdőmeridián irányába, +y tengelye pedig erre merőlegesen, nyugat felé mutat, a kezdőpontja pedig az 1900 és 1905 közötti időtartamra meghatározott közepes pólushely: a CIO (Conventional International Origin). Látható, hogy a pólus valóban periodikus mozgást végez, a pólus elmozdulása körülbelül 0,5" ≈ 10 m sugarú körön belül marad, de az amplitúdó nem állandó és a periódus sem egyenlő az Euler-féle 303 napos periódussal, hanem ennél lényegesen hosszabb: 405 és 457 nap között ingadozik - átlagosan mintegy 435 nap.
A pólusmozgás felfedezése utáni években Chandler amerikai csillagász kimutatta, hogy a pólusingadozás két domináns periódusból, egy 12 és egy 14 hónapos periódusból tevődik össze. Az utóbbit tiszteletére Chandler-periódusnak nevezték el. Néhány hónappal Chandler felfedezése után Newcomb már elméleti magyarázattal is szolgált: a 14 hónapos összetevő a Föld szabadnutációja, míg a 12 hónapos összetevő az úgynevezett kényszernutáció, amely az azonos periódusú globális meteorológiai jelenségek (tömegátrendeződések, például légtömegmozgások, hó- és jégtömegek olvadása és újraképződése stb.) következménye.
A 4. ábrán látható, hogy a pólus az óramutató járásával ellentétes irányban többé-kevésbé szabályos spirális pályán mozog. Ezek a spirális pályák körülbelül hat évenként hasonló jellegűek, a két frekvencia összeadódásából kialakuló lebegés következtében. Jól látható ez a lebegés a 4. ábra alsó részén, a pólusingadozás 1967 és 1979 közötti időszakra vonatkozó háromdimenziós képén. Ugyancsak ezt szemlélteti az 5. és a 6. ábra is, ahol a felső görbe a pólusmozgás x, illetve y irányú összetevője, alatta pedig a szétválasztott 14 hónapos, 12 hónapos és a maradék összetevők láthatók. Megállapítható, hogy a szabadnutáció és a kényszernutáció külön-külön is meglehetősen bonyolult folyamat. A Chandler-összetevőn például felismerhető egy fél évszázad körüli periódus, amely több más földfizikai folyamatban is jelentkezik, pontos okát azonban egyelőre nem ismerjük.
Az átlagosan 427 napos Chandler-periódus és a 303 napos Euler-periódus közötti különbség oka a Föld rugalmas viselkedése. Ha ugyanis a Föld nem merev - mint ahogyan az Euler-féle pörgettyűegyenletek megoldásakor feltételeztük - akkor a forgástengely elmozdulásának megfelelően a megváltozó centrifugális erő hatására tömege úgy deformálódik, hogy a tehetetlenségi főtengelye közeledik a forgástengelyhez. (Szélső esetben, ha a Föld folyadékszerűen viselkedne, akkor a tehetetlenségi főtengelye teljes mértékben követné a forgástengely elmozdulását - tehát a periódus végtelen nagy lenne, és így pólusingadozásról nem is lehetne beszélni.)
Ennek megfelelően a TE Euler-féle, és a TC Chandler-periódus hányadosa kapcsolatba hozható a Föld rugalmasságát jellemző Love-féle k számmal:
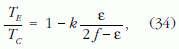
ahol f a Föld geometriai lapultsága, ε pedig a centrifugális és a nehézségi gyorsulás egyenlítői értékének hányadosa [5]. Az 1. táblázatban a (34) összefüggés alapján kiszámított, néhány szóba jöhető k értékhez tartozó Chandler-periódus hosszát tüntettük fel. A táblázatból látható, hogy a szabadnutáció Chandler-periódusa annál hosszabb, minél kevésbé merev a Föld. Az árapályjelenségek megfigyeléséből származó 0,29 és 0,31 közötti k értéknek 440 és 454 nap közötti periódus felel meg, viszont a pólusmozgás megfigyeléséből a 428-440 nap közötti Chandler-periódus tűnik a legvalószínűbbnek, amihez a táblázat adatai szerint k = 0,27-0,29 érték tartozik.
Ha meghatározzuk egy-egy teljes periódushoz a 4. ábrán látható póluspályák közepes pólushelyzeteit, akkor azt tapasztaljuk, hogy ezek a közepes pólushelyek az idő függvényében folyamatosan eltolódnak. A jelenséget szekuláris pólusmozgásnak, vagy pólusvándorlásnak nevezzük. A 7. ábrán látható, hogy az 1890 és 2000 közötti póluspálya már teljes egészében az 1900 és 1905 között meghatározott CIO középpóluson kívül halad. Az is látható, hogy a közepes pólus 110 év alatt több mint 10 m távolsággal vándorolt el Kanada irányában.
A megfigyelések szerint a pólusvándorlás mértéke viszonylag csekély - évente legfeljebb néhány dm (néhány ezred szögmásodperc) nagyságrendű -, a földtörténeti időskálán azonban ez az elmozdulás jelentős (több 10°) mértékű is lehet. Ezért a pólusvándorlás problémája a geológia és a geofizika sokat tárgyalt kérdése; különösen a paleoklimatológiai és újabban néhány globális tektonikai kérdés megválaszolása szempontjából igen fontos.
Kizárólag a pólusmozgás hatását figyelembe véve az ω forgási szögsebességvektor állócsillagokhoz viszonyított helyzetét gyakorlatilag állandónak tekinthetjük. Ekkor viszont állandó az égi egyenlítő síkjának helyzete is, tehát a csillagok saját mozgásától eltekintve, ezek égi egyenlítői (ekvatoriális) koordinátái az időben változatlanok. Ugyanakkor a Föld felszínén fekvő valamennyi pont helyzete (például a pontok szintfelületi földrajzi koordinátái) a forgástengelyhez rögzített geodéziai koordináta-rendszerekben a Föld tömegének a forgástengelyhez viszonyított elmozdulása miatt folyamatosan változik.
A pörgettyűmozgás elmélete szerint a szabad tengely körül forgó merev testek helyzete akkor stabil, ha a forgás megindulásakor a test forgástengelye megegyezik a tehetetlenségi főtengelyével. Ellenkező esetben, vagyis ha a forgás nem a tehetetlenségi főtengely körül indul meg, akkor a forgó test helyzete - erőmentes térben is - állandóan változik, azaz a test szabadnutációs mozgást végez. Így, ha valamely merev bolygó esetében valamikor kialakult a szabadnutációs mozgás, akkor ennek fenntartásához semmiféle mechanizmusra nincs szükség.
Mivel a Föld nem merev test, rá ez a megállapítás nem érvényes. A Föld esetében a minimális mozgási energiájú állapot a tehetetlenségi főtengely körüli forgás. Ettől eltérő helyzetű forgástengely esetén olyan belső tömegátrendeződések lépnek fel, amelyek a két tengely közeledését, illetve egybeesését igyekeznek előidézni. A Chandler-összetevő vizsgálata alapján az a csillapítási idő, amely alatt a mozgás amplitúdója e-ed részére csökken körülbelül 10-30 év közötti értékre becsülhető [2]. Az ennél jóval hosszabb idejű megfigyelések azt bizonyítják, hogy léteznie kell valamilyen gerjesztő folyamatnak, amely a pólusmozgás ismeretlen módon elnyelődő energiáját valamilyen formában pótolja.
A lehetséges disszipációs és gerjesztési folyamatok napjainkban még nagyrészt tisztázatlanok, mivel az eddig felmerült lehetőségek általában más módon nehezen ellenőrizhetők és a számítások igen bonyolultak.
A fentiek szerint nyilvánvaló, hogy a Föld nutációs mozgásának oka a Föld bonyolult belső tömegeloszlása és a tömegek állandó mozgása, áthelyeződése. A Földön kívüli tömegek eloszlásának, a különböző égitesteknek a pólusmozgásra semmilyen hatása nincs.