
Fizikai Szemle honlap |
Tartalomjegyzék |
Nagy Mária, Radnóti Katalin
ELTE TTK Fizikai Intézet
A statisztikus fizika témakörének feldolgozása kikerült a középiskolai tananyagból, pedig szemléletesen, analógiákkal tárgyalva sok diák fantáziáját megmozgathatná. A téma feldolgozása azért is ajánlható, mert kapcsolatot teremt a fizika és a kémia világa között. Jelen írásunkban arra teszünk javaslatot, hogy bizonyos elemek miként kerülhetnek sorra a statisztikus fizika témaköréből például a fakultációs órákon, tehetséggondozás keretében. A tanulók ekkorra már a középiskolai fizika és kémiai kötelező tanulmányaik végére értek. A feldolgozásra ajánlott témakörök a különböző tantárgyakban megtanult ismeretek szintetizálásban is segítik a tanulókat.
Tanulmányunkban bemutatunk egy változatot arra, hogy a Boltzmann-eloszlás témakörébe tartozó problémák tanulmányozása miként lehetséges középiskolások számára megfelelő mélységben, amelyet iskolai környezetben ténylegesen ki is próbáltunk.
A fizikát emelt szinten tanuló, illetve reáltagozatos tanulók esetében a fizikai fogalmak kialakításánál használhatunk a tanterven kívül eső matematikát (esetünkben az exponenciális függvények ismeretét), így segítve a mélyebb megértést. A számolással kapcsolatos tevékenység a reál beállítottságú diákokat olyan világba engedi be, ahol hamarosan otthonosan mozognak. E módszer fontos eredménye, hogy így megadhatjuk diákjainknak a kellő alapozást az eredményes egyetemi szerepeléshez. Javasolt témánk feldolgozásán keresztül a diákok tanulási folyamatát elősegítve igyekszünk áthidalni a középiskola és az egyetem közti nagy szintkülönbséget, hogy az egyetemre bekerülve minél kevesebb problémájuk legyen.
Jelen feldolgozási javaslatunkban azt tartjuk a legfontosabbnak, hogy példákat mutatunk a mérési eredmények kiértékelési lehetőségeire. Írásunkban a következő témákat érintjük, amelyek differenciált csoportmunkában dolgozhatók fel:
A mérés célja, hogy megvizsgáljuk miként változik a légnyomás a h magasság függvényében, és méréssel alátámasszuk a barometrikus magasságformulára a szakirodalomból ismert exponenciális alakú összefüggést:
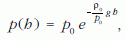
ahol p0 a légnyomás, ρ0 a levegő sűrűsége a választott nulla szinten.
Eszközök: a légnyomás magasságtól való függésének mérése magasabb házban (esetünkben az ELTE TTK épületében) könnyen megvalósítható egy manométer (1. ábra bal oldala) és egy hosszúságmérő eszköz (például vonalzó) segítségével.
Mi is gyárthatunk nyomásmérőt, ha boltokban megvásárolható termoszpalackot kétfuratos gumidugóval látunk el, és a két furat egyikébe U alakú folyadékmanométer- csövet, a másikba szelepet teszünk. A manométercsőbe (színezett) vizet töltünk. Ez fogja jelölni a nyomást úgy, hogy egyik vége a palack légterébe nyílik, a másik a levegőbe. Amikor a szelep nyitott állapotban van, a két vízoszlop magassága megegyezik az U alakú cső két szárában. Amikor a szelep zárt, a termoszban uralkodó és a külső légnyomás különbsége a manométerrel mérhető.
A mérés menete: ki kell választani egy referenciaszintet – erre az épület legalacsonyabb pontja ajánlott –, ahol eszközünkben a 2 vízoszlop egyenlő magasságánál a szelepet elzárjuk. Majd menjünk fel az épület legmagasabb szintjéig! Ekkor a folyadékszintek változni fognak. Minden szinten jelöljük vagy írjuk fel a 2 folyadékoszlop magasságának Δx = x1-x2 különbségét (1. ábra jobb oldala)!
Határozzuk meg az egyes emeletek referenciaszinttől mért Δh magasságát (például egy lépcső magasságát megmérjük, és a lépcsőket számoljuk)!
Kiértékelés, görbeillesztés: mért adatainkat vezessük táblázatba, ahol az emeletek függvényében szerepelnek a folyadékszint-különbségek, a referenciaszinttől mért távolság és a nyomáskülönbség. Az ELTE TTK-n mért adatok az 1. táblázatban láthatók, a 3. emeleti kiugró értéket a továbbiakban nem vesszük figyelembe. A kapott nyomásadatokra exponenciális görbét – például Origin programmal – illesztve a 2. ábrán látható görbét kapjuk.
Az exponenciális magasságformula kis magasságkülönbségek esetén lineáris összefüggéssel is jól közelíthető. Illesszünk a pontokra egyenest is (3. ábra)! Valóban, az egyenes szépen illeszkedik a mérési pontokra, meredeksége pedig a magasságformulában szereplő exponens értékére utal.
A Fizikai Szemle 2013. évi első számában Gallai Ditta írásában gimnáziumi tanulók a János-hegyen végeztek hasonló méréssorozatot. Abban az esetben is közel lineáris függvény adódott a nyomásértékek magasságfüggésére, hiszen hasonlóan kicsik voltak a magasságkülönbségek.
A mérés célja, hogy megvizsgáljuk a reakciósebességi állandó értékének függését a hőmérséklet nagyságától, illetve alátámasszuk az Arrhenius-összefüggésként ismert exponenciális kapcsolatot. A kiértékelés részeként számítsuk ki a kémiai reakció aktiválási energiáját!
Felhasznált eszközök: 7×2 = 14 db kémcső, kémcsőállvány, mérőhenger, cseppentő, 7×3 cm3 reagens sósavoldat (HCl vizes oldata), 7×5 cm3 0,1 M-os fixírsóoldat (Na2S2O3 vizes oldata), desztillált víz, digitális hőmérő, Teklin-égő, kémcsőfogó, főzőpohár, jég és videókamera a kísérlet archiválásához.
A mérés menete: Végezzük el a következő kísérletet! Öntsünk össze szobahőmérsékletű vízfürdőben (T1 = 285,45 K) fixírsó vizes oldatát (nátrium-tioszulfát vizes oldata) sósavoldattal (hidrogén-klorid vizes oldata), és írjuk fel a reakció végbemeneteléhez szükséges időt! A reakcióegyenlet:
Na2S2O3+2HCl = 2NaCl+H2O+SO2+ S.
A reakció során csapadék képződik: kén válik ki, az oldat megsárgul (4. ábra). A mérés során azt az időkülönbséget jegyezzük fel, ami az oldatok összeöntése és az opálosodás között telik el!
Ismételjük meg a kísérletet magasabb, T2 = 330,35 K hőmérsékletű vízfürdőben, és ekkor is írjuk fel a reakció idejét!
Végezzük el a fenti méréseket különböző hőmérsékleteken (jeges, illetve melegített vízfürdőben elérhető hőmérsékleteken), közben ügyeljünk arra, hogy mindig ugyanolyan mennyiségű oldatokat öntsünk össze. E miatt használunk kétszer 7 darab kémcsövet, így tudjuk előkészíteni a kiindulási anyagmennyiségében végig állandó elegyet. A reakció végeredménye minden mérésnél ugyanaz, ezért a kén végső koncentrációja, azaz a koncentrációváltozás is állandó lesz. Most is jegyezzük fel a hőmérsékletekhez tartozó reakcióidőket! Referenciamérésként valamelyik hőmérsékleten mérjünk többször!1
Megfigyelhetjük, hogy magasabb hőmérsékleten sokkal gyorsabb a reakció, oldatunk sokkal hamarabb besárgul.
Elméleti magyarázat: Ismert, hogy az aktiválási energia elérése szükséges a kémiai reakciók végbemeneteléhez, azaz a molekulaszerkezet megbolygatásához ezt az értéket elérő, elegendően nagy energiával kell ütközniük a molekuláknak.
Az aktiválási energia elérésére magasabb hőmérsékleten lényegesen több részecske képes, így a hőmérséklet emelkedésével erőteljesen megnő a reakció sebessége.
A k reakciósebességet, a T abszolút hőmérséklet és az egy részecskére jutó Ea aktiválási energia függvényében az Arrhenius-egyenlet adja meg:
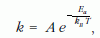
ahol kB = 1,38 · 10-23 J/K, a Boltzmann-állandó, A a koncentrációra jellemző állandó. Ez az Arrhenius-egyenlet fizikai értelemben vett (egy részecskére jutó) energiát tartalmazó alakja.
Az Arrhenius-egyenlet moláris aktiválási energiát tartalmazó – kémikusok által használt – formája pedig:
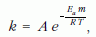
ahol R = 8,314 J/molK, az egyetemes gázállandó, m az Avogadro-szám, Eam pedig az egy mólnyi mennyiségre vonatkoztatott aktiválási energia.
Kiértékelés, görbeillesztés: Mért adatainkat vezessük táblázatba, ahol szerepelnek a mért abszolút hőmérsékletek (T) és reciproka (1/T), reakcióidők (t) és a reakcióidők másodpercben kifejezett számértéke reciprokának természetes alapú logaritmusa (ln(1/t ))! E két, reciprokot tartalmazó kifejezés értelmére majd az Arrhenius-egyenlet linearizálásakor derül fény.
A T abszolút hőmérséklet – t reakcióidő adatpárokat (2. táblázat) ábrázoljuk Descartes-koordinátarendszerben (5. ábra)! Látható, hogy a pontokra közelítően egy exponenciális függvény illeszthető. Tegyük meg ezt az illesztést például Origin programmal! Ahhoz, hogy az Arrhenius-egyenletből aktiválási energiát is számíthassunk, egyenesre – mint legkönnyebben illeszthető függvényre – van szükségünk, a kérdéses energia az egyenes meredekségéből számítható. Az Arrhenius-egyenlet mindkét oldalának vegyük a logaritmusát, ekkor a fizikusok által kedvelt egyrészecskés egyenletből a
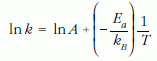
lnk és 1/T közötti lineáris kifejezésre, míg a moláris aktiválási energiát tartalmazó – vegyészek által használt – egyenletből a
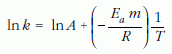
szintén lineáris összefüggésre jutunk. Mivel k a reakciósebesség, azaz arányos 1/t-vel, ezért a reakcióidő másodpercben kifejezett számértéke reciprokának természetes alapú logaritmusa (ln(1/t )) és 1/T között is lineáris lesz a kapcsolat. Ezt ábrázoltuk a 6. ábrán.
Megjegyzés: Magát a k-t csak kémiai számítások árán kapnánk meg, ami nem anyaga egy fizika fakultációnak, de minket csak a reakciósebességi állandó hőmérséklettel való kapcsolata érdekel, így – egy egyszerűbb kémiai összefüggés és matematikai eszközök segítségével – elkerülhetjük a kémia tananyag mélyebb felhasználását.
A kapott egyenes – Origin program kiértékelése szerinti -b = -5405±182 meredekségéből az egyetlen részecske aktiválási energiája, felhasználva a b = -Ea/kB összefüggést:
A moláris aktiválási energia pedig:
Diszkusszió: Az 5. ábrán látható grafikon, valamint a linearizált 6. ábra alátámasztja, hogy a reakciósebességi együttható értéke az abszolút hőmérséklet szerint exponenciális függést mutat. Ezzel a megállapítással és az aktiválási energia értékének megadásával numerikusan ismerkedtünk meg az Arrhenius-egyenlettel.
A tényleges kémiai számításokat elvégezve, azaz a koncentrációval és egyéb kémiai mennyiségekkel számolva az egyenes meredekségére -5407-et kapunk. Tehát jól számoltunk a mélyebb kémiai ismeretek kikerülésével is. Mindkét meredekség számításakor éltünk azzal a feltétellel, hogy az elvégzett kísérlet nem egy pontos reakciókinetikai mérés, mivel csak vizuálisan észlelhető ponthoz tartozó időt tudjuk mérni, amelynek a következő hibái vannak:
Továbbá meg kell jegyezni:
Ezekkel a hibákkal viszont nincs probléma, hiszen a demonstrációs kísérletnek nem kell kinetikai vizsgálat szempontjából korrektnek lennie.
Ez a módszer az aktiválási energia számítására csak akkor alkalmas, ha a reakció egyszerű és termikus aktiválású.
A víz gőznyomása függ a hőmérséklettől, a gőznyomás változása a hőmérséklet függvényében szintén exponenciális, Boltzmann-eloszlást követ.
Az eddigi példákhoz hasonlóan most ezt az állítást fogjuk alátámasztani mérési eredmények kiértékelésével. Továbbá becslést adunk a víz párolgáshőjére az Arrhenius-egyenletnél számolt aktiválási energiához analóg módon.
A következőkben az interneten található mérési adatokat fogunk elemezni. Ez több szempontból fontos és előnyös. Egyrészt a tanulók élvezik, ha a világhálóhoz kapcsolódik a tanulás folyamata. Másrészt egyetemi tanulmányaik során gyakorta kényszerülnek hasonló eljárásra. Előnyös, ha már középiskolában lehetőségük van megtanulni és megszokni a procedúrát.
Az adattáblázat internetes elérhetősége: http://hu.wikipedia.org/wiki/Víz_(adattáblázat)
A víz tenzióját folyékony víz felett elemezzük. Az elektronikus táblázatban szereplő összetartozó abszolút hőmérséklet-nyomás (T-p ) adatpárokat ábrázolhatjuk (7. ábra). Illesszünk exponenciális görbét – például Origin programmal –, mert az a függvény láthatóan jól közelíti a pontpárokat!
Az Arrhenius-egyenlethez hasonlóan:
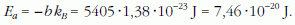
csak most a p gőznyomás szerepel a reakciósebesség és Lf forráshő az aktiválási energia helyett. Hasonló a moláris mennyiségre vonatkozó egyenlet is:
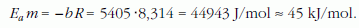
Most is linearizáljuk a görbét, mint az előző fejezetben:
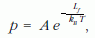
illetve
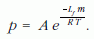
Ábrázoljuk a gőznyomás pascalban kifejezett számértékének természetes alapú logaritmusát az abszolút hőmérséklet reciprokának függvényében, majd a pontokra illesszünk egyenest (8. ábra)!
Az egyenes b meredeksége az Origin programmal való illesztés szerint: -5520±8,5. E meredekségből az Arrhenius-egyenlethez hasonlóan kiszámítható egy molekula "párolgáshője":
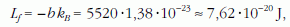
illetve a moláris párolgáshő:
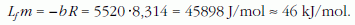
A táblázatokban szereplő vízre, amelynek minden kg-ja 55,5 mol, vonatkoztatott párolgáshő pedig:
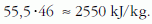
E két mennyiség irodalmi értéke: Lfm = 40,8 kJ/mol, illetve 2256,4 kJ/kg.
Diszkusszió: A 7. ábrán látható grafikon megfelel a víz gőznyomása korábban ismertetett exponenciális hőmérsékletfüggésének.
Továbbá sikeresen kiszámítottuk a víz párolgáshőjét (látens hő) az Arrhenius-egyenletnél számolt aktiválási energiával analóg módon. Az irodalmi értékektől való kis eltéréseket az okozza, hogy a párolgáshő valójában függ a hőmérséklettől, valamint az interneten található mérési eredményeknek van mérési hibája.
A fentiekhez hasonlóan még sok példa található a Boltzmann-eloszlással leírható jelenségekre.
Jelen írásunkban a Boltzmann-eloszlásra vonatkozó problémamegoldásokat mutattuk be. Kísérleti eredmények kiértékelésére, megvitatására és értelmezésére tettünk ajánlásokat, nem pedig hagyományos középiskolai fizika példatárakban szereplő feladatok megoldására. Az egyetemi laboratóriumi mérésekhez hasonlítható feladatokat állítottunk a tanulók elé.
Fakultációs órán történt tényleges kipróbálás tapasztalatai alapján kijelenthetjük, hogy a diákok képesek követni az újszerű feldolgozási módot, aktív részesei tudnak lenni az ilyen szemléletű tanóráknak.
A módszer segítségével a diákok bevezetést kapnak egy, a megszokott középiskolai szemlélettől eltérő felfogás elsajátításához. A tárgyalt témakör kapcsán olyan ismeretekre tesznek szert, amit egyébként az egyetemen teljesen újként, önállóan kellene megszerezniük.
Munkánk fontos célja volt az is, hogy a középiskolai és az egyetemi szint közötti különbség áthidalására tegyünk kísérletet az ajánlott feldolgozási folyamat segítségével. Azt szeretnénk elérni, hogy az egyetemek természettudományi karaira kerülő hallgatók fizika-, kémia-, környezettan- és földtudományszakon ne ütközzenek a szükséges szakmai alapok hiánya miatt tanulmányi problémákba. Úgy gondoljuk, hogy azok a tanulók, akik részesei voltak a cikkünkben leírt szemléletű oktatásnak, könnyebben sajátítják el olyan kurzusok tananyagát, amelyről valamilyen mélységben az egyetemi szemléletnek megfelelően már tanultak.
________________________
1 A mérések elvégzésében nyújtott segítségért köszönetet mondunk Róka András főiskolai docensnek.