
Fizikai Szemle honlap |
Tartalomjegyzék |
Szeidemann Ákos
Eötvös József Gimnázium, Tata
A címbeli kérdés kétértelmű, nem véletlenül. Egyrészt: szabad-e tanítanunk a tehetetlenségi erőket fizikaórán? Másrészről pedig felmerül: meg lehet-e tanítani a Coriolis-erőt mondjuk 9. évfolyamon? Elsőre egyáltalán nem egyértelmű a pozitív válasz. Korábban én is úgy gondolkoztam – ismerve az akkori tankönyvek szokásos gondolatmenetét a gyorsuló vonatkoztatási rendszerek témakörében –, hogy egyszerűbb ismeretek is nehezen adhatók át a diákoknak. Sokáig gondot okozott számomra az inerciarendszer fogalmának tanítása, illetve használata. Mindig úgy éreztem, többet kellene magyaráznom diákjaimnak a pontos megértéshez. Ma már tudom, hogy nem mindig szükséges a teljes precizitás, hiszen a diákok világképe hosszú idő alatt formálódik, de persze fontos rávilágítunk a nehézségekre.
A Newton-törvények megértése az egyik sarkalatos pontja a fizika tanításának. Az arisztotelészi kép erősen működik a gyerekekben, amit sokszor a dinamika tanulása közben sem lehet kellő szinten helyrerakni. Ez a jelenség elsősorban a tapasztalatoknak a nem adekvát fogalomrendszerrel való magyarázatára vezethető vissza. Az utóbbi években például egyre gyakrabban tapasztalom a kinematika tanítása közben, hogy a diákok "nagyszerűen" megtanulják az egyenletes mozgás út-idő összefüggését, de nem vesznek tudomást más típusú mozgásokról. Hosszú gyakorlás eredményeként lehet csak elérni, hogy változó mozgások esetén ne számoljanak az s = v · t képlettel [1].
A tehetetlenség törvényének értelmezése – látszólag – nem jelent gondot, hiszen az egyenes vonalú egyenletes mozgás jelenik meg benne, de a dinamika alaptörvényét csak mint begyakorolt matematikai formulát kezeli a legtöbb diák. A mennyiségek közötti logikai kapcsolat már nem tisztul le bennük, és zavaros számukra a vonatkoztatási rendszer szerepe is. Ezt nehezíti még az a tény, hogy a newtoni dinamika fogalomrendszerének "megszilárdulása" előtt más tantárgyból – alkalmazás szintjén – előkerülnek a forgó Földön tapasztalt áramlási jelenségek. A földrajz szaknyelve nem használja a vonatkoztatási rendszer és a gyorsulás fogalmát sem, így ott nem nyer értelmezést az erő és a sebességváltozás közötti szoros kapcsolat. Ezt tetézi az a – módszeres megfigyelések nélküli magyarázaton alapuló – tévképzet is, miszerint a fürdőszobai lefolyóban tapasztalt forgómozgást is a Föld forgása okozza.
Tehát arra a kérdésre, hogy szabad-e tanítanunk a tehetetlenségi erőket, határozottan az a válaszom, hogy igen, sőt megkockáztatom: kell tanítanunk ezt a témát, hiszen így nyernek a fogalmak igazi értelmet, és ezáltal segítjük a természetföldrajz tanítását is. Nem pusztán arról van szó, hogy a földrajzórán hallottakat megerősítjük, magyarázzuk, hanem olyan módszert választunk, amely a fizikatanítás sajátja, és termékenyen hathat más tárgyak, jelen esetben a földrajz tanulására. Az ilyen értelemben vett komplex, egymásra épülő természettudományos oktatásnak látom értelmét. Ez is az oka, hogy – véleményem szerint – nem járna sikerrel egy komplex természettudományi tárgy bevezetése (a természettudományi érettségi már működik, ami persze nem mond ellent állításomnak). Rögtön adódik a kérdés: megvalósítható-e az integrált természettudományos szemlélet, ha például fizikaórán a tantermi fizikára korlátozódunk és megmaradunk a klasszikus kísérletek szintjén.
A magyarországi oktatási gyakorlat erőteljesen épít a tankönyvre, mint tanulást segítő eszközre [2], ezért érdemes áttekintenünk a vonatkozó tartalmakat. A természetföldrajz témáit tárgyaló tankönyvek több fejezetben is foglalkoznak a Coriolis-erő komoly ismeretét feltételező tartalommal. Három forgalomban lévő, 9. évfolyamnak íródott földrajz tankönyvet vizsgáltam a Coriolis-erő fogalmának megjelenése szempontjából. Makádi Mariann és Taraczközi Attila [3] nem használják könyvükben a Coriolis-erő kifejezést, hanem a következőképpen fogalmaznak: "A ciklonokban a levegő kívülről befelé áramlik, mert a közepén alacsonyabb a légnyomás, mint a környezetében. Ám az áramló levegő súrlódik a felszínnel, és a Föld forgásából származó tehetetlenségi erő eltéríti eredeti irányából. Ezért a felszín közelében a levegő befelé, az északi félgömbön az óramutató járásával ellentétes irányban áramlik."
Nemerkényi Antal és Sárfalvi Béla [4] talán fölismerték azt a hiátust, amely a két tárgy tanítása közben fellép, ezért külön kiemelt részben foglalkoznak a Coriolis-erővel. A megértést segíti egy ábra is. Fontos azonban megjegyeznünk, hogy a kiemelt magyarázat is pusztán azt a szokásos gondolatmenetet használja, amely szerint az északi féltekén az É–D, illetve D–É irányú mozgást végző légtömegek "lemaradnak", illetve "megelőzik" a Földet, vagyis jobbra térülnek el. Ebben persze rejtve benne van, hogy a forgó rendszerben mozgó test esetén kell figyelembe venni ezt a hatást, de mi történne például egy K–NY irányú áramlás esetén?
Arday István, Rózsa Endre és Ütőné Visi Judit tankönyvírók is említést tesznek a Föld forgásából származó hatásokról a légkörben és a vízburokban is, de a részleteket nem fejtik ki. A légnyomás és a szél – Ciklonok, anticiklonok című leckében [5] a következőt olvashatjuk: "A szél mozgása a valóságban nem egyenes irányú, azaz a levegő nem pontosan az alacsony légnyomású területek irányába mozog, ugyanis ezt a légmozgást több tényező is befolyásolja. Ilyen a Föld forgásából származó kitérítő- (Coriolis-) erő, az ugyancsak ebből eredő centrifugális hatás és a földfelszín közelében ható súrlódás, amely a magasabb légrétegekben már elhanyagolható. A szél a valóságban az említett erők közös eredőjének irányába mozog."
Láthatjuk, hogy a tankönyvírók mennyire különbözőképpen próbálják megoldani a problémát. Nincsenek könnyű helyzetben: szerintem nem az ő feladatuk a Coriolis-hatás bevezetése. Azt a szemléletet, amely szükséges lenne a megértéshez, mindenképpen fizikaórán kellene elsajátítani. A diákok számára zavaró lehet, hogy fizikából gimnáziumban nem tanulnak hidrosztatikát és a tehetetlenségi erők sem részei a törzsanyagnak. Nagyobb gondot okozhat viszont az, hogy a fizikában az erő fogalma a mechanikai kölcsönhatáshoz kapcsolódik. Ahogy már a centripetális erő is fogalmi zavarokhoz vezethet [1], úgy a tehetetlenségi erők bevezetés nélküli használata akadályozza a fogalomrendszer letisztulását.
Ha az elmúlt évek feladatsorait alapul véve megvizsgáljuk a földrajz érettségi követelményeit, akkor megállapíthatjuk, hogy majd minden évben van olyan megoldandó feladat, amely épít ezekre az ismeretekre. Példaként említem a 2012. év egyik középszintű [6] feladatát, amely egy meteorológiai térképen látható légköri képződményhez kapcsolódóan tesz föl kérdéseket többek között a levegő vízszintes és függőleges mozgásáról. Egy 2010. májusi emelt szintű feladatsor [7] pedig konkrétan a Coriolis-erő hatásaival foglalkozik. Sajnos nincs olyan adatbázis, amely az érettségi feladatonkénti megoldottságát magában foglalná, de érdekes lenne megvizsgálni, hiszen pontosabb képet kaphatnánk arról, hogy a fizikai ismereteket is igénylő feladatokat (napsugárzás hatásai, környezeti áramlások) vajon milyen szinten tudják a fiatalok megoldani, összevetve a teljes feladatsorban mutatott teljesítménnyel.
A tatai Eötvös gimnáziumban négy éve működő Környezetfizikai szakkörön lehetőségem volt olyan tananyagokkal foglalkozni, amelyek mind tartalmi, mind módszertani szempontból fejlesztették tanári munkámat. A környezeti áramlások témája kapcsán foglalkoztunk Foucault-inga modellel, ciklonok modellezésével, frontok laboratóriumi vizsgálatával is. Az itt szerzett tapasztalataim alapján a Coriolis-hatás bevezetésének legjobb és legegyszerűbb módszere a következő fizikai logikai gondolatmeneten alapul.
Vizsgáljunk egy egyenletes egydimenziós mozgást, amelyet egy papírlapra húzott szakasz fog reprezentálni! A papírlapot egyenletesen forgatva egyszerűen bemutathatjuk a Coriolis-hatást. Ehhez vegyünk két A4-es papírlapot (1. ábra). Az egyiket vágjuk be a hosszabbik oldalának felezőpontjától a rövidebbik oldallal párhuzamosan a papírlap közepéig. A másik lapon is végezzük el a műveletet úgy, hogy a rövidebbik oldal felezőpontjából indulunk ki. A demonstráció első lépéseként illesszük össze a két papírlapot a vágások mentén úgy, hogy középpontjuk összeérjen. Ezután húzzunk vonalat az alsó papírlapra a másik papírlap vágott éle, mint vonalzó mentén (egyenes a 2. ábrán). A következőkben pedig ismételjük meg a vonalhúzást úgy, hogy a mozgás pályájának rögzítésére használt lapot egyenletesen forgatjuk (görbe a 2. ábrán).
A kapott egyenesen, illetve görbén végezzünk méréseket, számításokat. A 2. ábrán látható módon az egyenesen (értsd: a mozgás inerciarendszerből szemlélt pályáján), illetve a görbén (értsd: a mozgás forgó rendszerből vizsgált pályáján) is tegyünk jelöléseket az időegységenként elért pontokhoz. Ezeket megkaphatjuk, ha a kiindulási pontból különböző nyílásszögű körzővel (1 cm, 2 cm stb.) körívezünk. A továbbiakban az így kapott A-K (az egyenes pontjai), illetve A'-K' (a görbe pontjai) pontsorozattal dolgozunk. Az egyenes egyes pontjainak A-tól mért távolságát L-lel, az összetartozó pontokból (például BB') képzett szakaszok hosszát D-vel jelölve egy adattáblát készíthetünk.
Mérjük meg az L és D szakaszok hosszát, és határozzuk meg a D/L hányadost, amit közelítőleg, mint relatív eltérülés értelmezhetünk. Megállapítható, hogy a D/L hányados függ L-től, mégpedig nagyobb L távolsághoz nagyobb D/L relatív eltérülés tartozik (a későbbiek során bebizonyítjuk az egyenes arányosságot). Ha a görbét az előzőtől különböző v vonalhúzási sebességgel, illetve ω forgatási szögsebességgel állítjuk elő, az új trajektória nem lesz fedésben az első rajzunkkal. Kisebb v, illetve nagyobb ω egyaránt nagyobb relatív eltérülést eredményez. A mért adatok kvalitatív elemzésével eljuthatunk a

összefüggésig, hiszen fentiek alapján L és ω a számlálóban, v pedig a nevezőben kell, hogy szerepeljen. A dimenziók vizsgálatával könnyen látható, hogy akkor kapunk a jobb oldalon is dimenziótlan hányadost, ha L mellett ω és v is első hatványon szerepel.
A D/L hányados demonstrálja a Coriolis-hatás mértékét. Ha ez a hányados nagy, akkor az adott jelenségben a forgás trajektóriát befolyásoló hatása jelentős. (A hányados reciprokát Rossby-számnak nevezzük [8].)
A ceruza hegyének mozgása inerciarendszerben egy egyenes vonalú egyenletes mozgás:

A ceruza hegye alatt azonban elforgatjuk a papírlapot, ezért a mozgó papíron kirajzolódó pálya egy forgó vonatkoztatási rendszerben érvényes pályát jelöl. Az origóból indulva az inerciarendszerbeli mozgás és a papír szögsebességének mínusz egyszeresével mozgó egyenletes körmozgás összege adja a görbült pályát, amit a diákok a mozgó papíron saját maguk kirajzolnak. Ez jó demonstrációja a forgó Földön eltérülő trajektóriáknak, azaz a Coriolis-hatásnak.
A forgó rendszerben a (origóból induló) ceruza mozgása így írható le:
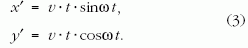
Ezen egyenletekből adódó mozgás trajektóriáját ábrázoltuk a 3. ábrán. A kísérletben kapott adatokat is – vékony keresztekkel – berajzoltuk ugyanerre az ábrára, a 3 mm mérési pontosságot feltüntetve. A sebesség- és a szögsebesség-paramétereket próbálgatással határoztuk meg úgy, hogy a mérési eredményekhez legjobban illeszkedjenek, és 2,9 m/s valamint 0,18 1/s-nak adódtak. A két ponthalmaz kielégítően fedi egymást. A kísérletben meghatározott D távolságok csak kicsit térnek el a (3) egyenletekből kapott elméleti pontok alapján számolt De távolságoktól.
A 4. ábrán szemléltetjük a t idő alatt L radiális elmozduláshoz tartozó φ szögelfordulást. A PP' ívhossz itt könnyen meghatározható az egyenletes forgás alapján: Se = L · φ = L · ω · t. Az origótól való távolodás is egyenletes: L = v · t. A két egyenletet egymással elosztva kapjuk az (1) egyenlet jobb oldalán is szereplő tagot:

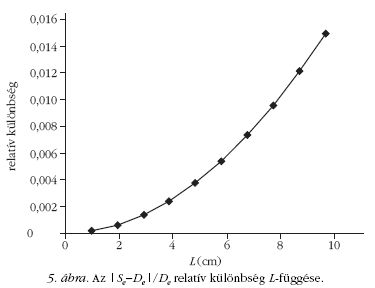
Az (1)-ben szereplő könnyen mérhető D/L érték helyett itt az S /L szerepel. A kettő közötti különbség (a vizsgált kis elfordulás-tartományban) elhanyagolható. Módszertani szempontból meg kell jegyeznem, hogy a tanítási gyakorlatban is gyakran alkalmazunk elhanyagolásokat számítási feladatokban, de ritkán járunk utána, hogy a közelítő számítás az adott esetben befolyásolja-e a következtetést. Nézzük meg, hogy a kísérlethez kapcsolódó elméleti számítás milyen eredményt ad e tekintetben (5. ábra), tudniillik, hogy a forgó rendszerben kapott görbéhez tartozó Se /L hányados (ahol Se az elméleti számítással kapott ívhossz) mennyire tér el az általunk használni kívánt De /L hányadostól (ahol De a 4. ábráról könnyedén leolvasható, az (5) egyenlet alapján számított forgásból származó elmozdulás).
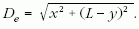
|
 |
Az 5. ábrán látható, hogy a demonstrációs kísérletben az Se (L) és a De (L) függvények között 2%-nál kisebb a különbség (ez nagy elfordulások vizsgálata során természetesen megnő). Így az (1) egyenletben megfogalmazott egyenes arányosság bizonyításának teljes gondolatmenete az alábbiakban foglalható össze.
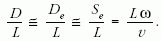
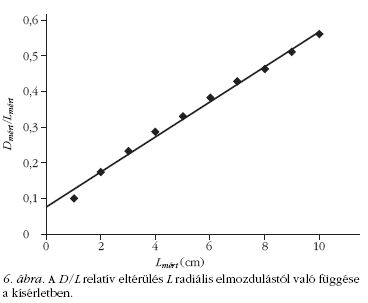
Látható, hogy így már nem pusztán egyenes arányosságról van szó, hanem egyenlőségről, amiből egyébként a Coriolis-gyorsulás képletében szereplő 2-es faktor is – itt nem részletezett módon – kijön. A D/L hányados L-lel való egyenes arányosságát a mért adatok is mutatják. A kísérleti adatainkból (2. ábra) a 6. ábrán látható egyenest kapjuk, amelynek meredeksége természetesen v-től és ω-tól függ. Az egyenes a vonalhúzás indítása és a forgatás indítása között eltelt idő miatt nem az origóból indul. A fenti, két egyenletes mozgás összetevésén alapuló modell ezért jól írja le a kísérletet. Bár a kísérleti pontatlanságok teljesen nem küszöbölhetők ki (például a távolságmérések), a vonalhúzás és a forgatás sebessége is a tapasztalat alapján állandónak tekinthetőek, ezáltal a demonstrációs kísérlet jól használható.
Alapfeltevésem az volt, hogy a Coriolis-erő bevezetése [9] nélkül is megvilágítható a jelenségkör lényege. Módszeremet eddig hat 9. évfolyamos csoportban próbáltam ki. Három csoportban saját diákjaim tanulnak, a többi hármat két másik tatai iskolából választottam ki. Ahhoz, hogy a módszertani hatást mérni tudjam, készítettem egy négy kérdésből álló tesztet, amelyet az óra elején, majd az óra végén is kivetítettem a diákoknak. A tanulók füzetükbe rögzítették az általuk helyesnek gondolt választ, amit az óra utolsó két percében összesítettem. A mérést a tanév végén végeztem, amikorra a résztvevők már foglalkoztak földrajz órán a ciklonokkal, és fizikából pedig terítékre került a teljes mechanika.
A papírlapos kísérletet a tanulók párban, esetleg hármasával egyszerűen el tudták végezni. A pályák megrajzolása után a diákok máris láthattak egy alapvető tapasztalatot, tudniillik hogy a mozgás leírása több nézőpontból is elvégezhető, és nem vezet azonos eredményre. A kapott görbe arra is utal, hogy a forgó rendszerből szemlélve a mozgást van gyorsulás. A párok, csoportok rajzait összehasonlítva azt is – szinte trivialitásként kezelve – megállapították a diákok, hogy a kapott trajektóriák nem feltétlenül egyformák: az egyenestől való eltérés mértéke függ a vonalhúzás v sebességétől és a forgatás ω szögsebességétől. Mért adataikból minden tanuló láthatta, hogy a D/L relatív eltérülés nő az L távolsággal. Motivált csoportban – akár házi feladatként is – az egyenes arányosság is megállapítható.
Az órán közösen nagyságrendi becslést adtunk az (Lω)/v hányadosra néhány – a megértés szempontjából fontos – mozgás esetén (1. táblázat ), ahol L a mozgásra jellemző távolság, v a mozgó objektum sebessége, ω pedig a Föld forgási szögsebessége. Alapvető célunk az volt, hogy a diákok a demonstrációs kísérlet során a relatív eltérülésre kapott összefüggés segítségével megállapíthassák, hogy a mindennapi életben előforduló Coriolis-hatás mennyire jelentős.
Az 1. táblázatban öt – közelítőleg vízszintes síkban történő – jelenséget vizsgálunk meg, ami a mozgás karakterisztikus hosszának 7 nagyságrendjét fogja át. Mindben körülbelül a 45. szélességi foknál tekintjük a mozgást és a Föld forgása az eltérülés okozója. Ezért ωFöld sinφ = ω függőleges = 5 · 10-5 1/s szögsebességet használtunk, ami az adott helyen a Föld szögsebességének a Föld érintősíkjára merőleges komponense. (A Falkland-szigetek – ahol az I. világháború és egyben a történelem utolsó tengeri ütközete zajlott, amely tisztán hadihajók közti tüzérségi párbajból állt – a déli szélesség 52. fokánál találhatók, de ez a nagyságrendi becslést nem befolyásolja.) A kád és a mosdó lefolyójában haladó víz sebessége egyre nagyobb, az utolsó 10 cm-t körülbelül 2-3 s alatt teszi meg egy úszó szappanbuborék. Ezzel alulról becsültük a haladási sebességet. A párizsi Pantheonban felállított történelmi Foucault-inga hossza 67 m, periódusideje 16 s volt. 5°-os kitéréssel számolva a kétszeres amplitúdó körülbelül 10 m-nek adódik, az ingatest átlagsebessége egy fél periódusból számolva 1,25 m/s. A táblázatban felsorolt 3–4. jelenség jellemző sebességét a ferde hajítás maximális távolságának formulájából számoltuk a dobás és a lövés távolságából kiindulva. Mindkét esetben a Coriolis-eltérülés nagysága az elvben mérhető tartományba esik. A ciklonok átmérőjét a meteorológiai adatok alapján 1000 km-nek, a benne áramló levegő sebességét egy erős szél sebességével becsültük (ebben az esetben az elméleti leírásunk eredményeként adódó (1) arányosság már semmiképpen sem igaz).
A hatásvizsgálathoz készített teszt kérdéseit és a lehetséges válaszokat a 2. táblázat tartalmazza, amelyben föltüntettem azt is, hogy a válaszadók (összesen 136 fő) hány százaléka jelölte az adott választ az óra elején, illetve az óra végén. Ha a változás az eredeti érték 20%-nál nagyobb mértékben nőtt, vagy csökkent, azt szignifikáns változásként értékeltem, és ↑, illetve ↓ nyíllal jelöltem.
A táblázatból egyértelműen látható, hogy a diákok a lefolyóval kapcsolatban tévhittel rendelkeztek (1.C válasz az óra elején 71%), illetve hogy a levegő áramlásával kapcsolatban hiányosak az alapvető fizikai ismereteik (4.D válasz az óra elején 51%). Noha az óra végén sem mindenkor a helyes választ jelölték meg a legtöbben, de mind a négy kérdés esetében korábbi tanult tudásukat mérhetően pontosították a diákok. A módszer hatékonyságát az igaz válaszok százalékának változása jól mutatja, ezek rendre +24%, +21%, +16%, +13%.
Az óra elején minden kérdésnél a legtöbb diák egy hamis választ látott jónak (ami tovább növeli a téma tanításának fontosságát). Az óra végén azonban mind a négy esetben csökkent ez az arány: -18%, -16%, -12%, -26%. A 3., illetve 4. kérdésnél ezzel az igaz válasz lett a leggyakoribb. A 2. kérdés esetén az alapjelenség megértését az A és a B válasz megjelölése adja vissza (a kettő közötti különbség az irányszabály, amire nem fektettem hangsúly). Az ezekre összesen adott válaszok aránya 12%-ról 38%-ra nőtt, miközben az egyértelműen hibás D válasz a kezdeti 43%-ról, 26%-ra esett. Sajnos az 1. kérdésnél a leggyakoribb válasz a tévhit maradt.
A 4. kérdés C válaszát talán azért jelölték meg az óra végén többen, mert nem elég egyértelmű a kérdés, de ráéreztek a válaszadók, hogy az eltérülés mértéke és az L méretparaméter között van összefüggés.
<>
Írásomban elsősorban arra mutattam rá, hogy a Coriolis-hatás az erő fogalma nélkül is bevezethető a középiskolában egyszerű, szemléletes és interaktív módon. Így a tehetetlenségi erők megértésének nehézségeit [10] megkerülve adhatunk mélyebb magyarázatot a légköri és óceáni áramlásokkal kapcsolatos néhány jelenségre.
Ez az egyszerű fizikai kísérlet, kiegészítve más laboratóriumi kísérletekkel [11] és terepi megfigyelésekkel jó példa arra, hogyan illeszthető a természetföldrajz tanítása a természettudományok közvetlen tapasztalatokon alapuló megismerési metodikájához.
Köszönöm témavezetőm, Horváth Ákos a cikk finomra hangolásához nyújtott hasznos tanácsait.