Neugebauer Tibor
Egyetemi Fizikai Intézet
Budapest

Amint tudjuk, fémek elektromos ellenállása normális hőmérsékleten a hőmérséklettel nő és ezt a tapasztalatot az elmélet is. igazolja. Már Drude és Lorentz klasszikus elektronelmélete szerint is az ellenállás az abszolút hőmérséklet négyzetgyökével arányos. Persze, ez a klasszikus elmélet ma már teljesen elavult, azonban az elektromos ellenállásnak modern hullámmechanikai elmélete szerint is, amely Blochtól származik, normális hőmérsékleten az ellenállás az abszolút hőmérséklettel, míg igen alacsony hőmérsékleten ennek ötödik hatványával arányos. Ezen elméleti eredményeket a kísérletek igazolják is olyan mérvben, amint ez várható ; tudjuk ugyanis, hogy a fémek elektronelmélete csak egy ideális határesetet tárgyal (mely szerint szabad elektronok mozognak egy periódusos erőtérben) és ezért az eredményei inkább csak kvalitatívek. Tény azonban; hogy a fémek ellenállása alacsony hőmérsékleten a hőmérsékletnek egy magasabb hatványával arányos. Ha tehát extrapolálunk az abszolút zéruspontra, ott az ellenállásnak el kell tünnie.

Igen meglepő volt azért Kamerlingh Onnes-nek az az 1911-ben tett felfedezés e; hogy egyes fémek elektromos ellenállása az abszolút zéruspont fölött néhány fokkal úgyszólván hirtelen teljesen eltűnik. Higanynál, amellyel ő eredetileg kísérletezett, ez 4,17° K-nél következik be, alumíniumnál 1,14-nél, ónnál 3,69-nél, ólomnál 7,26-nál stb., az abszolút zéruspont fölött.

Hogy belássuk ezen jelenség elméleti értelmezésének nehézségeit, vegyük először szemügyre az elektromos ellenállás klasszikus és modern elméletét. Drude és Lorentz klasszikus elektronelmélete szerint a fémek belsejében szabad elektronok vannak, melyek tulajdonképpen a fématomok levált vegyértékelektronjai: Ezek a fém belsejében úgy viselkednek; mint egy gáz és reájuk az említett szerzők az akkor egyedül ismeretes és minden esetben érvényesnek vélt klasszikus Boltzmann-statisztikát alkalmazták. Eszerint az elektronok, ha elektromos tér nincs jelen, a fém belsejében össze-vissza mozognak, mint a gázmolekulák egy gázban. Ha azonban a kérdéses fémdarab két végpontja között egy elektromotoros erőt alkalmazunk (pl. galvánelemet kapcsolunk rá), akkor minden elektronra hat a fellépő elektromos tér és az előbb említett rendszertelen mozgásra egy egyirányú áramlás szuperponálódik. Ennek dacára sem lép azonban fel egy állandóan gyorsuló mozgás, mert az elektronok mozgásuk közben állandóan a fémionokba ütköznek és ezeknek mozgási energiájuk egy részét leadják. Tehát végeredményben egy állandó középsebességű áramlás lép fel, melyet mi mint elektromos áramot észlelünk; az elektronoknak a rácsionokba való ütközése okozza az elektromos ellenállást, míg a rácsionoktól felvett ütközési energiát, mélynek folytán ezek rezgésbe jönnek, mi mint Joule-féle hőt észleljük. Egészen világos, hogy ezen elmélet alapján a szupravezetést nem lehet megmagyarázni, mert semmi módon nem lehet levitatni azt a körülményt, hogy az elektronok a rácsionokba ütköznek. A fémeknek ez a klasszikus elektronelmélete a normális ellenállást igen jól látszott megmagyarázni, de más téren súlyos ellenmondásokra vezetett a tapasztalattal. A fém belsejében lévő elektrongáznak t. i. fajhőjének is kellene lennie, még pedig, mivel a klasszikus statisztika szerint minden szabadsági fokra ½ R fajhő, vagy helyesebben atomhő, jut (R az abszolút gázállandó), azért megfelelően a mozgás 3 szabadsági fokának ³/2 R nagyságú additív fa hőnek kellene minden fémnél az elektrongáz jelenléte miatt a normális fajhőhöz járulnia, de ennek kísérleti úton a nyomát sem találni.

A kvantummechanika és ezzel kapcsolatban a Fermi-Dirac-statisztika felfedezése után Sommerfeldnek sikerült ezt a paradoxont megmagyaráznia. Ő a fém belsejében lévő elektrongázra a klasszikus Boltzmann-statisztika helyett az elektronok esetében kizárólag érvényes Fermi-Dirac-statisztikát alkalmazta és kimutatta, hogy ekkor a kérdéses fajhő tényleg eltűnik, amint azt mindjárt beláthatjuk, ha meggondoljuk, hogy a fém belsejében lévő elektrongáz teljesen el van »fajulva«, ami azt jelenti, hogy minden elektron a Fermi-Dirac-statisztika által megengedett legmélyebb energiaállapotban van. Tehát a fém lehűtésével már nem tudunk tőlük energiát elvonni, vagyis az elektrongáz fajhője zérussal egyenlő.

A fajhő problémáját tehát az új elmélet megoldotta, az elektromos ellenállás kérdésében azonban egy nagy nehézség lépett fel. A hullámmechanika szerint ugyanis az elektronok áramlását úgy kell tekintenünk, hogy egy síkhullám terjed a fémrácsban. Egy fémion természetesen szórná ezt a hullámot, akárcsak a fényt. Egy rendezett ionrács azonban nem, amint azt mindjárt beláthatjuk, ha arra gondolunk, hogy bármely irányban is számítanánk a szórást, az összes fémiontól szórt hullámok - (mivel a rács teljesen rendezett) interferencia folytán mindig teljesen lerontják egymást, vagyis az elektronhullám akadálytalanul (anélkül, hogy szórást szenvedne) hatol át a fémionok rácsán, vagyis az ellenállás eltűnik. (A szórási irányok közül csak a Bragg-féle reflexiós irányok tennének kivételt, de ezek szerepe a jelen esetben érdektelen.) Az előbbi okoskodásból tehát az következne, hogy a fémeknek egyáltalában nincs ellenállása és ez persze teljes abszurdum.

Ezen a helyzeten aztán Bloch segített, aki kimutatta, hogy az elektromos ellenállás hullámmechanikailag úgy jön létre, hogy a fémionok termikus mozgást is végeznek (egyensúlyi helyzetük körül rezegnek) és ez a mozgás azt hozza magával, hogy a fémrács minden pillanatban kissé eltér a teljesen rendezett állapottól, tehát mégis tudja szórni az elektronhullámot, vagyis az elektromos ellenállásnak a fémionok hőmérsékleti mozgása az oka. Hasonlóan hatnak szennyezések is, mert ezek is rontják a rácsnak a szimmetriáját. Bloch elméletének igen szép igazolása Mathiessen kísérleti úton talált törvénye, amely szerint a fémek ellenállása normális hőmérsékleten egy az abszolút hőmérséklettel arányos tagból és egy a hőmérséklettől független tagból tevődik additive össze. Az első rácsionok hőmérsékleti mozgásától a második a szennyezésektől származik és ezek mennyiségével arányos.

Láthatjuk mindezekből, hogy a vezetés kvantummechanikai elmélete szerint sem tudjuk a szupravezetés felléptét egyszerűen megmagyarázni, mert egyrészt egyáltalában nem vitathatjuk le a rácsionok termikus mozgását az abszolút zéruspont fölött még néhány fokkal sem, azonkívül persze, teljesen szennyezés mentesnek sem tehetjük fel a vizsgált fémeket.

Mielőtt tovább tárgyalnánk a szupravezetés elméleti magyarázatának lehetőségeit, még néhány érdekes tapasztalatot szeretnénk megemlíteni. Elsősorban is egy igen érdekes és fontos dolog, hogy nem azon fémek válnak szupravezetőkké, amelyeket az elektrotechnika mint a legjobb vezetőket ismer. Így sem a réz, sem az ezüst nem szupravezetők. Az elektrotechnikában használatos vezetők közül csak az alumínium szupravezető, de ennek is igen mélyen van az ugráspontja. Míg a magasabb ugrásponttal bíró szupravezetők (mint pl. Hg, Sn, Pb stb.) normális hőmérsékleten rosszvezetők. Egy másik ilyen érdekes körülmény a következő: Amint említettük, Bloch kvantummechanikai elmélete szerint mély hőmérsékleten az ellenállás az abszolút hőmérséklet 5. hatványával arányos. Bloch elmélete persze csak azt az ideális határesetet tárgyalja, melyben teljesen szabad elektronok mozognak a fémrács periódusos terében. Azonban, éppen ezen körülményből, hogy egy valódi fém ellenállása mennyire követi Bloch elméletét, következtethetünk arra, hogy a benne lévő elektronok mennyire tekinthetők szabadoknak és erre a kérdésre vonatkoznak MacDonald és Mendelsohnnak 1948-ban végzett mérései alkáliák elektromos ellenállására 20 és 4° abszolút közt. Ők a Bloch-elmélettől megkívánt 5-ös hatványkitevő helyett, a következő értékeket találták: Li-nál 4,52, Na-nál 4,85, K-nál 3,2, Rb-nál 2 és Cs-nál 1,4. A legutolsó adat már eléggé bizonytalan. Amint tehát látjuk, lithiumnál is már elég szabadok az elektronok, míg nátriumnál úgyszólván teljesen szabadok. Ezért tehát azt várnók, hogy elsősorban a Na legyen szupravezető, míg a tapasztalat szerint az eddig elért legmélyebb hőmérsékleteken sem vált egyetlen alkálifém sem szupravezetővé.

A szupravezetés jelenségét matematikailag persze úgy írhatjuk le, hogy az ugrásponton az ellenállás zérussá, vagy a vezetőképesség végtelen naggyá válik. Hogy azonban fizikailag meg tudjuk magyarázni ezt a jelenséget, ahhoz bizonyítani kellene tudni, hogy van a kérdéses fémeknek egy olyan legalsó energiaállapota, melyben egy egyirányú elektronáramlás lép fel, anélkül, hogy vele egyidőben egy egyenlő nagyságú, de ellenkező irányú áramlásnak is kellene szükségszerűen fellépnie. Vagyis egészen hasonló viszonyoknak kellene fellépniök, mint amilyenek a ferromágneses jelenségeknél tényleg ismeretesek. Ezeknél egy elemi tartományon belül t. i. a legalsó állapotban az elemi kis spinmágnesek mind egymáshoz parallel állnak be, ezt Heisenberg elmélete szerint a köztük működő kvantummechanikai ú. n. kicserélődési erők okozzák. Makroszkopikusan egy test azután úgy lesz mágneses, hogy ezen elemi tartományok mágnesezési irányait rendezzük. Így kellene tehát lennie a szupravezetőben is, hogy ilyen elemi tartományok áramlási irányainak rendezése révén állna elő a makroszkopikus áram. Az előbbi feltételünket még egy kissé enyhíteni is lehet, nem szükséges ugyanis, hogy az említett állapot a legmélyebb legyen, lehet egy kissé magasabb is, csak legyen olyan nagy statisztikai valószínűsége, hogy a fém még igen alacsony hőmérsékleten is legnagyobb ideig ezen állapotban legyen. Közvetlenül beláthatjuk persze, hogy ezen követelmények megvalósításának milyen nehézségei vannak, amíg mágneses jelenségeknél az egyirányú orientálódást könnyen sikerült minden kétséget kizáróan megmagyarázni, addig a jelen esetben egy ilyen áramlási aszimmetria fellépte igen nehezen gondolható el. A szupravezető fémek nem tartoznak ugyan mind egy kristályrendszerbe, de mind igen magas szimmetriájú rendszerben kristályosodnak, továbbá igen bajos valami kapcsolatot feltételezni egyirányban áramló elektronok közt stb. Megemlítjük még végül, hogy D. Bohm egy, a múlt ősszel megjelent dolgozatában, hivatkozva Blochnak egy régebbi tételére, elméleti úton azon következtetésre jut, hogy a posztulált egyirányú elektronáramlás elméleti lehetetlenség.

Ha azonban még sikerülne is a szupravezetőkőn észlelt végtelen nagy vezetőképességre valami elméleti magyarázatot találni, még akkor is megmagyarázatlan maradna egy, a szupravezetőket jellemző további effektus, melyet felfedezőikről Meissner-Ochsenfeld-effektusnak nevezünk. Ha egy fémdarabot mágneses térbe viszünk, akkor tudjuk, hogy benne örvényáramok indukálódnak, ezek az áramok az elektrotechnika elemi törvényei szerint mindig olyanok, hogy mágneses terük az indukáló mágneses tér ellen hat, vagyis a mágneses erővonalaknak a kérdéses fémdarabba való behatolását igyekszik meggátolni. Mivel ezek az örvényáramok azonban egy normálisan vezető fém esetében az ohmikus ellenállás folytán igen gyorsan elhalnak, a mágneses tér igen gyorsan be tud hatolni és eltekintve azon esetről, melyben a fém ferromágneses, praktice ugyanúgy megy keresztül a fémen, mintha az egyáltalában nem is lenne jelen. Egészen másképp áll azonban a dolog a szupravezetőknél, náluk, mivel nincs ohmikus ellenállás, az indukált áramok megmaradnak és a terük éppen akkora lesz, hogy az indukáló mágneses erővonalakat kiszorítja a kérdéses fémdarabból, vagyis a mágneses tér nem tud behatolni a szupravezetőbe. Mindezen dolgok az elektrotechnika ismert törvényszerűségeiből következnek, pusztán azon feltevés segítségével, hogy a szupravezető ellenállása zérus.

Ha azonban eredetileg még normálvezető állapotban helyezzük a kérdéses fémdarabot mágneses térbe, akkor természetesen egy másodperc kicsiny törtrészei után a mágneses tér erővonalai akadálytalanul áthatolnak rajta. Ha ezután a mágneses térben hagyva lehűtjük az ugráspontja alá, akkor az elektrotechnika törvényei alapján azt várnók, hogy a szupravezetőállapot bekövetkezte, mivel a fémdarab állandóan a mágneses térben volt, a mágneses erővonalaknak benne való lefutását nem fogja befolyásolni. A tapasztalat azonban egészen mást mond. A szupravezető ezen esetben is kidobja magából a mágneses erővonalakat, vagyis teljesen mindegy, hogy előzőleg hűtjük-e le a kérdéses anyagot az ugráspontja alá és aztán visszük mágneses térbe, vagy fordítva, először tesszük a mágneses térbe és aztán hűtjük le, az eredmény mindkét esetben ugyanaz ; a szupravezető a mágneses erővonalakat kiszorítja magából. Ezt a jelenséget, melyet már pusztán egy végtelen nagy vezetőképesség feltevésével nem lehet megmagyarázni, Meissner-Ochsenfeld-effektusnak nevezzük. Mindezen dolgok egy egyszeresen összefüggő (nem gyűrűalakú) szupravezetőre vonatkoznak. Gyűrűalakú szupravezetőnél az a jelenség lép fel, hogy ha először mágneses térbe helyezzük és aztán lehűtjük az ugráspontja alá, akkor persze a gyűrű üregén azért áthatolnak mágneses erővonalak, ha ezután a szupravezetőállapotban most kikapcsoljuk a mágneses teret, akkor a gyűrű üregéből a mágneses erővonalak nem tudnak kiszabadulni, mert hiszen ekkor keresztül kellene menniök a gyűrűn, de ez nem lehetséges, mivel ez szupravezető és azért kidobja magából a mágneses erővonalakat, tehát ezen erővonalak befagynak a gyűrű üregébe és gyűrűn kívül záródnak, vagyis a mágneses tér lekapcsolása után a gyűrű úgy fog viselkedni, mint egy mágnes. Ez a jelenség azonban nem olyan feltűnő, mint az előbb említett, mert hiszen úgy is leírhatjuk, hogy a mágneses tér megszűnése áramot indukál a gyűrűben és mivel ez szupravezető, az áram nem szűnik meg, tehát a mágneses tere is megmarad.

A fentemlített Meissner-Ochsenfeld-effektus az egyszerűen összefüggő szupravezetőnek még egy érdekes leírását teszi lehetővé. Tudjuk ugyanis, hogy a paramágneses (és még inkább ferromágneses) anyagok magukba sűrítik a mágneses erővonalakat, míg a diamágnesesek azokat magukból kiszorítani igyekeznek, tehát ritkítják azokat; (a diamágnesség azonban mindig igen kicsiny). Tudjuk továbbá hogy a mágneses permeabilitás µ és az 1 cm³-re vonatkoztatott mágneses szuszceptibilitás közt a következő összefüggés áll fenn

(1)

A mágneses permeabilitás adja meg, hogy a mágneses erővonalak hányadrésze hatol keresztül a kérdéses testen, azért ez paramágneses anyagoknál mindig egynél nagyobb; míg diamágneseseknél egynél kisebb. Ezek alapján tehát az egyszerűen összefüggő szupravezető Meissner-Ochsenfeld-effektusát úgy írhatjuk le, hogy ennél, mivel minden mágneses erővonalat kidob magából µ = 0 és ezt az eredményünket (1)-be téve

(2)

vagyis

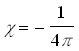(3)

Ezt az utóbbi eredményt nevezzük szupravezető abszolút diamágnességének. Természetesen, ez a normálisan diamágneses testek diamágneses szuszceptibilitásával szemben óriási. Az irodalomban általában egy grammatom vagy grammolekulányi anyag szuszceptibilitását szokás megadni, a diamágneses szuszceptibilitás ekkor 10^-6 nagyságrendű, míg (1)-ben a szuszceptibilitás 1 cm³ anyagra vonatkozik, tehát ennélfogva az említett nagyságrendnél még kisebb; összehasonlítva ezt az adatot (3)-mal, látjuk, hogy a szupravezető abszolút diamágnessége milyen óriási. Természetesen, azért nem is gondolhatunk arra, hogy ezt a szuszceptibilitást csak úgy egyszerűen, úgy mint a közönséges diamágneses szuszceptibilitásnál, az egyes atomok szuszceptibilitásának összegeként értelmezzük, kétségkívül itt egy más természetű jelenségről van szó.

A szupravezetés jelenségének a megmagyarázására már igen sok elméletet próbáltak felállítani. Mielőtt azonban ezek közül a fontosabbak megbeszélésére reátérnénk, még néhány szót kell szólnunk London elméletéről, melynek nem célja ugyan a szupravezetésnek egy természettudományi magyarázatát adnia, hanem pusztán az elektrodinamika differenciál egyenleteinek a szupravezetőkre vonatkozó helyes felállítására törekszik és azonkívül szintén nem magyarázza meg, de logikusan beépíti a differenciálegyenletekbe a Meissner-Ochsenfeld-effektust.

Írjuk tehát fel a két Maxwell-féle differenciálegyenletet azon esetre, amelyben a mágneses. térintenzitás és az indukció egymással egyenlőnek vehető; (nem ferromágneses anyagokról van szó) akkor

(4)

és

c rot E = - , (5)

ahol H a mágneses és E az elektromos térintenzitást jelenti, I az áramsűrűség, e a dielektromos állandó és c a fénysebesség. A (4) jobboldalán lévő második tagot azonban elhagyhatjuk, mivel a végtelen nagy vezetőképességű szupravezető belsejében nem lesz eltolódási áram, tehát

(6)

Vegyük továbbá tekintetbe, hogy feltevésünk szerint a szupravezető belsejében az elektronok teljesen szabadok, akkor felírhatjuk a következő egyenletet

(7)

ahol - e az elektron töltése; m a tömegé és a gyorsulása. Mivel másrészt az áramsűrűség I a v sebességgel arányos, azért E és közt (7) alapján szükségképpen a következő összefüggést kapjuk

(8)

ahol egy konstans. (6) egyenletünket most differenciáljuk az idő szerint és azután behelyettesítjük (8)-at, akkor

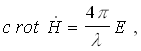(9)

Képezzük (9) egyenlet mindkét oldalán a rotációt

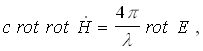(10)

továbbá, mivel a H egy divergenciamentes erőtér, ezt még így is írhatjuk

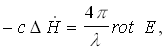
ahol a Laplace-operátor. Ide behelyettesítve (5)-öt, végül a következő eredményt kapjuk:

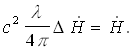(11)

Tegyük fel, hogy a szupravezetőnk felülete az YZ-síkban fekszik, míg az X-tengely a szupravezető belseje felé mutat és keltsünk a külső térben egy a Z-tengely irányával párhuzamos homogén mágneses erőteret. Ekkor, mivel a Laplace-operátorból csak az X -szerinti második differenciálhányados marad meg, tehát

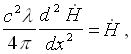(12)

a megoldás a következő alakú

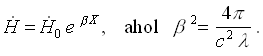(13)

Ezen egyenlet időszerinti integrálásánál fellép egy konstans, amely azonban a mi esetünkben, mivel a térnélküli állapotból indultunk ki, nullával tehető egyenlővé, tehát

(14)

(14) egyenlet tulajdonképpen a Meissner-Ochsenfeld-effektust írja le, mivel szerinte egy igen vékony határrétegtől eltekintve, a mágneses tér nem tud a szupravezetőbe behatolni, ill. ott exponenciálisan eltűnik. London (hipotétikusan) mindig elhagyja az integrációs konstanst, vagyis (11) helyett a

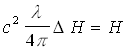(15)

egyenlet vezeti be. Evvel a Meissner-Ochsenfeld effektus ugyan nincsen megmagyarázva, de bele van dolgozva a matematikai elméletbe.

London azonkívül az (5) egyenletbe beteszi (8) eredményünket, tehát a

(16)

egyenletet írja fel és itt ugyancsak nullával teszi egyenlővé (hipotétikusan) az idő szerinti integrálásnál fellépő konstanst, tehát a

(17)

egyenletre jut. Azonkívül (16)-ban helyébe ismét bevezeti (5)-ből a rot E-t, tehát a

(18)

egyenletet kapja és ebből szükségképpen arra következtet, hogy a mennyiség mint egy u függvény gradiense állítható elő, tehát

(19)

London ezután még érdekes következtetéseket vont le ezen u függvény természetére vonatkozólag.

Amint említettük, London elmélete nem adja a szupravezetés jelenségének természettudományi magyarázatát és ez nem is célja, hanem pusztán a kísérleti tapasztalatok helyes matematikai megfogalmazására törekszik.

A szupravezetés tulajdonképpeni természettudományi megmagyarázására felállított igen sok elméleti próbálkozás közül, persze, nem célunk valamennyit ismertetni és a régebbiek közül csak azokat említjük meg, amelyek, ámbár mostani tudásunk alapján már elavultak, mégis tartalmaznak egy olyan gondolatot, amely modern elméletek kiinduló pontjául szolgált vagy szolgálhat.

Benedicks elmélete szerint normális hőmérsékleten az elektronok az atommagok körül a Bohrféle pályákon keringenek, igen alacsony hőmérsékleten azonban ezen atomok olyan közel jutnak egymáshoz, hogy az említett Bohr-féle pályák »érintkeznek« és ezért egy elektron úgy mozoghat, hogy egy félkört az egyik atommag körül, a következőt azonban a következő atommag körül futja be a másik oldalon, aztán az innensőn ismét a harmadik körül és így tovább. Vagyis a kérdéses elektron egy kígyózó vonal mentén halad a fémben, amely csupa fél Bohr-féle körpályából áll. Jelenlegi tudásunk szerint ez a feltevés teljesen elavult, mert hiszen igen jól tudjuk, hogy a fém nem atomokból, hanem pozitív iónokból és egy kvazi-szabad negatív elektrongázból áll. Egy jó gondolat azonban van Benedicks elméletében és ez az, hogy amint természetesen az elektronok ellenállás nélkül keringenek a Bohr-féle pályákon, ugyanúgy az ellenállás hiányának a szupravezetőknél is valami hasonló jelenségnek kell lennie.

Egy másik ilyen érdekes régebbi elmélet Kronigé. Ennek megértése céljából egészen Habernek egy régi a fémek kohéziójára vonatkozó elméletére kell visszamennünk. Tudjuk, hogy az alkalihalogenidkristályok (pl. a kősó) úgy vannak felépítve, hogy egy egyszerű szabályos rács pontjain felváltva negatív halogén- és pozitív alkaliiónok vannak és a rács kohéziójának legnagyobb részét egyszerűen ezen iónok kölcsönös elektromos vonzása okozza. Haber az alkalifémek kohézióját hasonló módon próbálta megmagyarázni. Az alkáliák, mint tudjuk, ú. n. felületen centrált rácsban kristályosodnak. Az egyes rácspontokon pozitív alkalii1ónok vannak. Haber feltevése szerint az ezen iónoktól leadott negatív elektronok viszont ezen rács üresen maradt közeit foglalnák el, vagyis ugyanúgy, amint az alkalihalogenidek rácsában váltakozva pozitív alkali- és negatív halogeniónok vannak, az alkalifémeknél hasonlóan pozitív alkaliiónok és negatív elektrónok építenének fel egy hasonló rácsot és ezek elektrosztatikus vonzása lenne a fémes kohézió oka. Napjainkban Haber elmélete már teljesen elavult, mivel igen jól tudjuk, hogy a pozitív alkaliiónok rácsában a negatív elektrónok nem szintén egy rácsot, hanem egy csaknem teljesen elkent negatív töltéselosztást képeznek. Az elektronok kicsiny tömegük miatt és az ú. n. nullapontmozgás következtében nem is maradhatnának az egyes rácspontokon. Kronig bizonyos mérvben Haber elméletét újította fel az ő szupravezetési elméletében. Szerinte ugyanis normális hőmérsékleten tényleg úgy van, hogy a negatív elektronok töltése a pozitív iónok rácsában teljesen el van kenve, vagyis ezen elektronok össze-vissza mozognak, de egy szupravezetőnek az ugráspontján ez az »elektronfolyadék« megfagy és egy Háber-szerű elektronráccsá alakul át. Kronig elméletének tehát egy nagy előnye lenne, hogy a szupravezető ugráspontját mint az elektronrács olvadáspontját lehetne értelmezni és ez teljesen természetessé tenné azon körülményt, hogy a szupravezető ugráspontja egy meghatározott hőmérséklet, ugyanúgy, mint ahogyan bármely szilárd test olvadáspontja is az: A szupravezetés tulajdonképeni oka azután Kronig szerint az lenne, hogy amíg az ugrásponton felül az »elektronfolyadék«-ban levő egyes elektronok össze-vissza mozognak és a rácspontokba ütköznek és ennélfogva ohmikus ellenállás lép fel, az ugrásponton alul a merev elektronrácsot csak mind egészet, tehát ütközések nélkül lehetne csak elmozdítani, energiaveszteség, tehát ellenállás ilyen módon nem léphetne fel. Kronig későbbi dolgozataiban aztán már nem is egy egész merev rácsot vett fel, hanem lineáris merev elektronláncoknak a mozgására gondolt a supravezetőben. Persze már Kronig elmélete is. elavult, mert most már igen jól tudjuk, hogy az elektronok Fermi-Dirac-statisztikát követnek, tehát olyan nullapontmozgásuk van, hogy a legalacsonyabb hőmérsékleten sem képezhetnének egy merev rácsot vagy láncot.

Még egy érdekes gondolat volt Frenkelé, aki arra mutatott rá, hogy egy végtelen nagy vezetőképesség egy végtelen nagy dielektromos állandóval egyenértékű, tehát a szupravezetés magyarázata ezen oldalról is megkísérelhető.

A második világháború utáni elméletek közül elsőnek Heisenberg-ét említjük meg. Az ő gondolatmenete a következő:

A fém belsejében mint tudjuk, az elektrongáz egy elfajzott Fermi-Dirac gáz, az elektronokat tehát kötik a Fermi-Dirac-statisztika előírásai és azért nem mozoghatnak pusztán az elektrosztatikus kölcsönhatásuk következtében szabadon. Azon csekélyszámú elektron azonban, melyek energiája maximális, más nincsen a statisztika korlátozó előírásainak alávetve és ezért csak a nagyhatótávolságú coulombtaszításuknak kölcsönösen engedelmeskedve egy bizonyos térbeli rendben helyezkedik el, amelyet bizonyos közelítésben mind egy sokszoros ióntávolságokból felépített (mivel csak kevésszámú elektronról van szó) rácsot foghatunk fel. Erre vonatkozólag azután egész hasonlóan lehet okoskodni, mint Kronig elméletében. A szupravezetés ezen elmélet szerint minden elektronvezető általános tulajdonsága lenne, kivéve a ferromágneses anyagokat, csak az ugráspontokban lenne különbség. Tehát olyan fémeknél, amelyek tapasztalatunk szerint nem lesznek szupravezetők, pusztán ezen ugráspontok feküdnének rendkívül alacsonyan. Heisenberg egy tanítványa ki is számította az alkalifémeknek az ugráspontjait ezen elmélet alapján és arra az eredményre jutott, hogy éppen ezen fémek ugráspontjai fekszenek különösen magasan, már pedig a tapasztalat szerint az alkaliák egyáltalában nem válnak szupravezetőkké. Heisenberg ezért már többször módosította az elméletét és azonkívül még további feltevések bevezetésével a Meissner-Ochsenfeld efektust is igyekezett az elméletével megmagyarázni, amelyet az eredeti formájában megmagyarázni nem tudott.

Egy másik fontos ilyen új elmélet Borné. Tudjuk, hogy a fémek belsejében minden hullámmozgás részére vannak ú. n. Bragg-féle reflexiós irányok (úgy amint ez a röntgenfény diffrakciójának az elméletéből ismeretes). Ha tehát az elektronok energiáit az ú: n. impulzustérben tüntetjük fel, akkor az egész impulzustér ennek folytán ilyen ú. n. Brillouin-zónákra esik szét, amelyeket ezen irányoknak és feltételeknek megfelelő impulzusok választanak el egymástól. Másrészt az elektronok eloszlása a Fermi-Dirac-statisztika szerint az impulzustérben egy gömbfelületen belül van. Ha már most egy Brillouin-zóna ezen gömbfelületen belül van, akkor elektronokkal telt, ellenkező esetben üres. Mivel azonkívül az elektronok kölcsönhatása a fémráccsal csak a Brillouin-zónák sarkain erős, azért Born feltevése szerint a szupravezetés létrejöttéhez az kell, hogy sok ilyen sarok közel feküdjön az előbb említett Fermi-gömbhöz. A legfelső betelt Brillouin-zóna sarkaiból ekkor az erős Coulomb kölcsönhatás felemel egyes elektronokat a feljebb fekvő be nem telt zóna nívójára, ha ez azonkívül aszimetrikusan történik, akkor előáll a spontán egy irányban folyó áram, tehát a szupravezetés. A szupravezetők ezért vannak Born szerint a periódusos rendszer két széles oszlopában, mert ezek egyik zónája vagy teljesen telt, vagy teljesen üres, mi az átmeneti fémeknek le nem zárt zónáik vannak. Ötvözetek akkor szupravezetők, ha a Brillouin-zónák szempontjából az egyik hiányát a másik feleslege pótolja, stb. Ezen utóbbi kérdésekkel főkép Born munkatársa Kai Chia Cheng foglalkozott. Megjegyezzük azonban, hogy egyrészt Born elmélete sem adja a posztulált elektromozgási aszimetria közvetlen magyarázatát, másrészt a Meissner-Ochsenfeld-effektus sem következik belőle minden további nélkül, mivel csak végtelen nagy vezetőképességet szolgáltat.

Egy érdekes újabb gondolat volt még a szupravezetést és a hélium II. úgynevezett szuperfluiditását egymással összefüggésbe hozni próbálni. A közönséges hélium (a 4-es atomsúlyú) ugyanis egy 2,19° absolútnál levő átalakulási pontján alul rendkívül érdekes fizikai tulajdonságokat vesz fel, amelyet röviden úgy jellemezhetünk, hogy sokkal folyékonyabbá válik minden eddig ismeretes folyadéknál. Egy érdekes gondolat volt tehát feltenni, hogy talán a szupravezetés és ez a szuperfluiditás hasonló jelenségek, vagyis közös okuk van. Ez azonban csak akkor volna lehetséges, ha a statisztika ezen jelenségeknél nem játszana szerepet, mivel az elektronok Fermi-Dirac, míg a héliumatomok Bose-Einstein-statisztikát követnek. Azonban éppen legújabban Reynolds és munkatársai kimutatták, hogy tiszta hármas atomsúlyú helium (amely Fermi-Dirac statisztikát követ), még az elérhető legmélyebb hőmérsékleten sem mutatja a szuperfluiditás jelenségét, és ezért az említett összefüggés erősen vesztett a valószínűségéből. Ogg még úgy próbálta megmenteni a helyzetét, hogy feltette, hogy a szupravezetésnél nem egyes elektronok, hanem mindig elektronpárok mozognak (ezekre ekkor t. -i. a Bose-Einstein-statisztika lenne érvényes ugyanúgy, mint a közönséges heliumatomokra), de Osborn kimutatta, ezen feltevés tarthatatlanságát.

Végül még néhány a szupravezetőkre vonatkozó érdekes tapasztalatot említünk meg: A szupravezetők különböző rácstípusokban kristályosodnak, de az ugrásponton a rácstípus nem változik, sőt még a rácsállandó sem, amint ezt Keesom és Kamerlingh Onnes, valamint Mc Lennan, Allen és Wilhelm igen gondos mérései igazolták. A fajhőnek az ugrásponton egy kis anomáliája van, szupravezető állapotban a fajhő kissé nagyobb. A hővezetőképességnek az ugrásponton szakadása van, szupravezető állapotban valamivel kisebb, a látszat az, mintha az elektronok egy része, mely normálvezető állapotban persze a hőt is vezeti, az ugráspont alatt ezen hővezetésből kikapcsolódna. (Mivel szupravezető elektronokká alakulnak át?) Az anyag optikai tulajdonságai Hilsch mérései szerint az ugrásponton egyáltalában nem változnak, ami egy igen meglepő tapasztalat volt, mert hiszen a végtelen nagy vezetőképességért felelős elektronoknak itt igen nagy jelentőséggel kellene bírniuk. Ezt a paradoxont azután Laue oldotta meg, aki elméleti úton kimutatta, hogy már az infravörös tartományban is csak a közönséges ohmikus vezetési mechanizmus, amely a szupravezető állapotban is a szupravezetési mechanizmus mellett változatlanul fennáll, bír egyedül jelentőséggel.

Mágneses tér a szupravezető állapot bekövetkeztét késlelteti, vagyis minél erősebb a tér, annál alacsonyabb hőmérsékleten válik a kérdéses fém szupravezetővé. Hasonlóan hat az elektromos árammal való terhelés is. Justinak sikerült kimutatnia, hogy szupravezetőknél egy a ferromágneses anyagoknál észlelt Barkhausen-effektushoz teljesen analóg jelenség lép fel, ha a mágneses térben levő szupravezető esetében a teret növeljük. Vagyis a normálvezető állapotba való átmenet nem folytonosan (pl. határfaleltolódásokkal) folyik le, hanem kicsiny tartományok ugrásszerű átmenetével. Legújabban azonban MacDonald és Mendelsohn folytonos átmeneteket is észleltek.

Nemcsak tiszta fémek, hanem ötvözetek is lesznek szupravezetők. Viselkedésük lényegileg ugyanaz, mint a tiszta fémeké, de az ugrásponton a mágneses teret nem dobják teljesen ki, hanem ennek egy része beléjük fagy. Ennek a jelenségnek valószínűleg azonban pusztán az az oka, hogy az ötvözet nem válik mindenütt egyidőben szupravezetővé és azért ugyanúgy bebörtönöz mágneses erővonalakat, mint a már említett gyűrűalakú test. Egy szupravezető is egy nem szupravezető fémből álló ötvözet ugráspontja általában mélyebben fekszik, mint a tiszta szupravezetőé, de ezen szabály alól kivétel a bizmut, amely ötvözetben a szupravezetők ugráspontját emeli anélkül, hogy maga is tiszta állapotban szupravezetővé válna. Az ónnak csak a fehér fémes változata, mely a négyzetes rendszerben kristályosodik; válik szupravezetővé, az ú. n. szürke ón, amelynek gyémántstruktúrája van, nem szupravezető.

Vegyületek is válnak szupravezetőkké. Egy ilyen tipikus példa a CuS, amely szupravezető anélkül, hogy akár a Cu, akár a S azok lennének.

Rádióaktív bétasugarak és mesterségesen felgyorsított elektronok is egy szupravezetőn való áthatoláskor ugyanúgy lefékeződnek, mintha a kérdéses fém normálvezető lenne, vagyis szó sincs arról, hogy ezen elektronok ellenállás nélkül hatolnának át a szupravezetőn.

Justi és munkatársainak Aschermann-nak, Friedrichnek és Kramernak a vizsgálatai szerint az eddig vizsgált anyagok között a NbN-nek a legmagasabb az ugráspontja még pedig a használt anyag tisztásági foka és kezelésétől függően 15-17° K, sőt egy esetben 20°-ot is mértek.

Az eddig ismeretes szupravezető elemek és ezek ugráspontjai (átalakulási hőmérsékletei) a következők :*)

_________________________
*) Állitólag a Re is szupravezetővé válik 0,9° körül.