Fizikai Szemle honlap

A JOULE-THOMSON EFFEKTUS

Radnai Gyula
ELTE, Általános Fizika Tanszék

1. Az ideális gáz belső energiája

Az állandó tömegű ideális gáz egyszerű termodinamikai rendszer, mivel egyensúlyi állapotát két független állapot­jelző egyértelműen meghatározza [1,2].

Ha független állapotjelzőkül a nyomást és a térfogatot választjuk, akkor az ideális gáz hőmérséklete az alábbi termikus állapotegyenletből kapható meg:

pV = RT    (n = 1 mólra)

Az ideális gáz belső energiáját pedig az alábbi kalorikus állapotfüggvény szolgáltatja:

U = U (p, V)

A fenomenologikus termodinamikának főtételekre alapozott tárgyalásakor a nulladik főtétel biztosítja a hőmérséklet egzisztenciáját, az első főtétel pedig a belső energia, egzisztenciáját minden termodinamikai rend­szerre. Így még a második főtétel előtt definiálhatunk egy empirikus hőmérsékleti skálát, valamelyik termo­dinamikai rendszer termikus állapotegyenletének felhasználásával.

A szokásos eljárás az, hogy referencia rendszernek éppen az ideális gázt választjuk, mert a pV = RT állapot­egyenletben a gázok anyagi minőségétől való függés nem szerepel. (Joggal választhatnánk például az ideális paramágneses szilárd anyagot is; az ideális gáz választásának történeti oka van.)

A második főtétel az entrópia egzisztenciáját biztosítja. Kiterjesztve az entrópia fogalmát összetett rendszerek nem egyensúlyi állapotaira is, a második főtétel segítségé­vel a folyamatok irányára is következtethetünk. Csupán egyensúlyi állapotokon keresztül történő idealizált folyamatok esetén is lehetővé válik azonban a második főtétel alapján egy olyan univerzális hőmérsékleti skála definiálása, amely független a hőmérsékletet mérő anyag állapotegyenletétől:

képlet

Vajon a pV = RT állapotegyenlettel definiált "ideális gáz hőmérsékleti skála" alkalmas-e olyan univerzális, "abszolút" hőmérsékleti skálának, amelynek létezését a második főtétel mondja csak ki? Igen.

Egy közvetett bizonyíték lehet a következő eljárás:

  1. Feltesszük, hogy ideális gázra

    pV = RT

    úgy, hogy T most a második főtétel segítségével definiált abszolút hőmérséklet.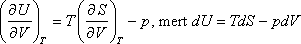
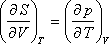
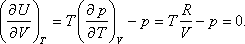
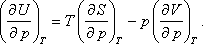
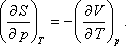
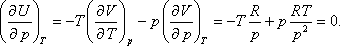
  2. Bebizonyítjuk a második főtétel felhasználásával, hogy ebben az esetben az ideális gáz belső energiája független a gáz térfogatától és nyomásától, csak abszolút hőmérsékletétől függhet. A térfogattól való függés:

    képlet

    Felhasználva a következő Maxwell relációt:

    képlet

    kapjuk:

    képlet

    A nyomástól való függés:

    képlet

    Felhasználhatjuk a következő Maxwell relációt:

    képlet

    Így kapjuk:

    képlet

  3. Feltesszük, hogy ideális gázra a

    pV=RT

    egyenlet nem más, mint T definíciója, vagyis a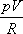

    képlet

    mennyiség egy empirikus, úgynevezett "ideális gáz hőmérséklet", és e definíció alapján gőzhőmérőt készíthetünk.
  4. Megvizsgáljuk kísérletileg, vajon igaz-e, hogy az ideális gáz belső energiája csak a pV szorzattól függ. Vagyis megvizsgáljuk, hogy igaz-e a 2. pontban bebizo­nyított állítás akkor is, ha a pV = RT-ben T az ideális gázzal hitelesített hőmérsékleti skála.

    Egyik ilyen kísérlet az, amikor összehasonlítjuk az ideális gáz két tetszőleges olyan egyensúlyi állapotát, melyben belső energiája (és mólszáma) egyenlő, de nyomása és térfogata is más-más értékű.

    Megmérjük mindkét állapotban a hőmérsékletet (empirikus, ideális gáz skálán), és megvizsgáljuk, egyenlő-e a két hőmérséklet.

    Ha igen, akkor ez azt jelenti, hogy az ideális gáz belső energiája csak a pV = RT-vel definiált empirikus, ideális gáz hőmérséklettől függ.

    Elvileg megfelelő kísérlet erre az, amelyet először (1807-ben) Gay-Lussac végzett el, majd Joule a múlt század 40-es éveiben megismételt, részleteiben is meg­vizsgált.
  5. Ha kísérletileg is megfelelő igazolást nyer az a feltételezés, hogy az ideális gáz belső energiája csak az ideális gáz hőmérséklettől függ, akkor ebből már az első főtétel alapján következik, hogy az ideális gáz egy izo­termikus folyamatban ugyanannyi hőt vesz fel, mint amennyi munkát végez, s egy Carnot körfolyamatban a felvett és a leadott hők abszolút értékeinek hányadosa az ideális gáz hőmérsékletek hányadosával egyezik meg.

    Ugyanez igaz azonban a második főtétellel definiált abszolút hőmérsékletek hányadosára is!

    Ez azt jelenti, hogy az ideális gáz hőmérséklet arányos az abszolút hőmérséklettel.

    Kényelmi okokból az arányossági tényezőt 1-nek választjuk, s így az ideális gáz hőmérsékleti skála egyben abszolút hőmérsékleti skála lesz.

    (Mechanikában hasonló eljárást követünk akkor, ami­kor a gravitációs és a tehetetlen tömeg arányosságát bizonyító kísérletek - Eötvös, Renner, Dicke és mások kísérletei - közös eredményeként, egyenlőnek választjuk a kétféle módon definiált tömeg mértékegységét és mértékszámát.)

Fizikatörténeti háttér

Gay-Lussac a gázok közös viselkedését kutatta, az ideális gáz fogalma akkor még nem létezett. éppen az ő vizsgálatai vezettek azonban az ideális gáz absztrakciójá­hoz. Felállította alaptörvényeit, amelyeket 1807-ben saját és mások kísérleti tapasztalataira támaszkodva a következőképpen mondott ki: [3].
  1. Valamennyi gáz eredeti térfogatának 1/267 részével terjed ki, ha hőmérsékletét 1 fokkal növeljük;
  2. A gázok kitágulása független a nyomástól.

Érdemes megemlíteni, hogy Gay-Lussac már öt évvel korábban, 1802-ben publikálta a gázok hőtágulására végzett kísérleteinek eredményét. [4] Kísérleteit levegő­vel, oxigénnel, nitrogénnel és hidrogénnel végezte Laplace felkérésére, aki erősen hitt a gázok egyforma viselkedésében. Gay-Lussac 1799-től volt az Ecole Normale Politechnique hallgatója, s Laplace 1794 óta tanított ott. Az első, 1802-es publikációt követően Gay­-Lussacot nevezetes, léggömbön végzett kísérletei (1804, Biot-val közösen), majd olaszországi és németországi tudományos útjai (1805, Alexander Humboldttal közö­sen) kötötték le. 1806-ban tért újra vissza Berlinből Párizsba, ahol 1809-től lett az Ecole Normale Politechni­que kémiatanára. Az 1807-es publikációt megelőző évek­ben Dalton és Davy Angliában, Volta pedig Itáliában végzett hasonló méréseket.

A hőanyagelmélet teljes virágzását élte, forradalmian új gondolatok kémiában születtek ekkor. A flogiszton­-elméletet Lavoisier kvantitatív kémiai kísérletei döntöt­ték meg, az anyag atomos felépítésének hipotézise ekkor kezdett erőre kapni. Először a gázok kémiai reakcióinak magyarázatára született meg Dalton atom és molekula­hipotézise. Ebbe a kutatásba kapcsolódott be Gay-­Lussac is, ezért volt mindkettőjük számára fontos, hogy a gázok azonos tulajdonságait keressék.

A gázok egyforma hőtágulása mellett Gay-Lussac felállította a gázok egyforma fajhőjének hipotézisét is. Pontosabban azt állította, hogy a gázok fajhője nem függ a gázok sűrűségétől (térfogatától). Ennek igazolására végezte el azt a kísérletet, melyet a következőkben ismer­tetünk. Ez a kísérlet egyrészt a második főtételt alátá­masztó egyik közvetett bizonyítéknak tekinthető, más­részt az első főtétel felfedezéséhez vezető egyik fontos lépés is volt a fizika történetében.

2. Gay-Lussac kísérlete - mai értelmezéssel

Vegyünk két azonos V térfogatú edényt, melyek a csappal vannak összekötve (1. ábra).

Az egész rendszer legyen kívülről adiabatikusan szige­telve, ezt jelképezi az ábrán ferdén vonalkázott keret. Kezdetben legyen ideális gáz csupán a baloldalon (a jobboldalon tehát vákuum van), így a kezdőállapot jellemzői:

p1; V1 = V; T1; U1

1. ábra
1. ábra

Nyissuk ki a csapot! Irreverzibilis, nem egyensúlyi állapotokon keresztül történő folyamat során a gáz kiterjed.

A folyamat végére az ideális gáz újra egyensúlyi álla­potba kerül, e végállapot jellemzői:

p2; V2 = 2V; T2; U2,

Állítás: U1 = U2
Bizonyítás: Az első főtétel értelmében

U2 - U1 = Q + W

Most Q = 0 az adiabatikus szigetelés miatt, W = 0 mert a termodinamikai munka külso munka, s a környezet nem végzett a gázon munkát.

Akármilyen gázzal is végezzük el a Gay-Lussac kísér­letet, a gáz új egyensúlyi állapota tehát mindig ugyanolyan belső energiájú, mint a kiindulási állapot volt. A hőmérsékletet mérni kell.

Gay-Lussac úgy végezte el a mérést, hogy az edénye­ket folyadékfürdőbe állította, s azt mondta, hogy ha T2 ≠ T1, akkor ez megváltoztatja a folyadékfürdő hőmérsékletét. (Elvileg igen, a hőkapacitások közti óriási különbség miatt azonban a gáz hőmérsékletválto­zása gyakorlatilag mérhetetlenül kis változást okoz a folyadékfürdő hőmérsékletében). Gay-Lussac nem kapott hőmérsékletváltozást, ezért arra következtetett:

T2 = T1

Ma már tudjuk, hogy az állítás helyes, de mint a fenti kísérletből levont mérési következtetés nem fogadható el. Gay-Lussac kísérletének mégis fizikatörténeti jelentősége van. Az a felismerés, hogy az ideális gáz szabad tágulásakor hőmérséklete nem változik meg, mind az energiafogalom kialakulásában, mind az ideális gáz kinetikus modelljének felállításában fontos szerephez jutott.

Idézzük csak fel Robert Mayer nevezetes gondolat­kísérletét! A hő és a munka közti kapcsolat felismerésé­hez vezető egyik fontos gondolata az volt hogy amennyi­vel több hő kell az ideális gáz 1°-kal való felmelegítéséhez állandó nyomáson mint állandó térfogaton, annyi munkát végez a gáz az izobár tágulás közben. Dehát ebben a kétféle folyamatban azonos kezdőállapot esetén a gáz két különböző végállapotba jut! A következtetés pedig csak akkor jogos, ha ugyanabból a kezdőpontból ugyan­abba a végállapotba jut mindkét esetben a gáz. Ehhez a kiegészítéshez volt szüksége Robert Mayernek Gay­-Lussac kísérletére (2. ábra).

Az 1 állapotból kétféle módon visszük át a gázt a 2 állapotba:

  1. munkavégzés nélkül, csak hőközléssel. Ez két lépésben hajtjuk végre: először állandó térfogaton felmelegítjük ΔT-vel, majd engedjük szabadon tágulni (miközben hőmérséklete a Gay-Lussac kísérlet tanulsága alapján állandó marad);
  2. munkavégzés közben, izobár módon, a szükséges hő befektetése mellett.

A hőközlések közti különbség:

Qp - QV, = CpΔT - CVΔT

2. ábra
2. ábra

A végzett munka:

W = pΔV = RΔT    mert a folyamat izobár.

Így jutunk az azóta már Robert Mayerről elnevezett összefüggéshez:

Cp - CV = R.

Semmi kétség: a Gay-Lussac kísérlet irreverzibilis folyamat, (ezért is ábrázoltuk a folyamatot a pV diagra­mon szaggatott vonallal). A kezdő és végállapot azonban egyensúlyi, ezért kiszámítható az entrópianövekedés. Ez ugyanannyi, mintha például hőtartályba ágyazva, izotermikusan vinnénk az ideális gázt a megadott kezdőálla­potból a megadott végállapotba, tehát


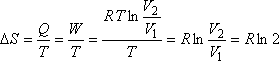képlet

(ha V2 = 2V1)

Csakhogy hőtartályba ágyazva ugyanennyivel csökken a hőtartály entrópiája, s így a

{hőtartály + gáz}

összetett rendszer entrópiája nem változik, ahogyan azt egyensúlyi folyamatok során el is várjuk. Ebben az egyensúlyi folyamatban a gáz és a hőtartály entrópia­változása "kompenzálja egymást" (Clausius megfogal­mazása), míg az irreverzibilis szabad tágulás során a gáz entrópianövekedését nem kompenzálja semmi a környe­zetben.

A gáz entrópiája mindkét esetben ugyanannyit válto­zik, mivel a gáz ugyanabból a kezdőállapotból ugyanabba a végállapotba jut, s az entrópia - állapotjelző.

Fizikatörténeti háttér

A Gay-Lussac-kísérlettel nem az a baj, hogy irrever­zibilis, hanem az, hogy a mérési pontosság nem volt megfelelő.

Ezen igyekezett javítani Joule. Robert Mayer 1845-ben adta ki német nyelven azt a munkáját, amelyben fent ismertetett gondolatmenetét publikálta s amelyben Gay-Lussac 1807-es kísérletére támaszkodott. Joule 1843-ban végezte el Gay-Lussac kísérletének módosított változatát a következő módon.

A két azonos térfogatú edényt fémből készítette el, és külön-külön kaloriméterekbe helyezte el őket. A kalori­méterek térfogata csak kevéssel volt nagyobb, mint a fém­edényeké, így viszonylag kis kapacitású volt a folyadék, ami a fémedényeket a kaloriméterekben körülvette. Ő is a folyadékok hőmérsékletváltozását mérte, s ebből követ­keztetett a gáz hőmérsékletváltozására.

A kiindulási állapotban az egyik edényt vákuumra szivattyúzta le, a másik edénybe pedig annyi levegőt pumpált, hogy nyomása 22 atmoszféra lett. Ezután kinyitotta a csapot, s a következő hőmérsékletváltozáso­kat tapasztalta: azon az oldalon, ahol eredetileg a 22 atmoszférás levegő volt, a hőmérséklet 2,36 F°-kal lett kisebb, a másik oldalon a hőmérséklet 2,38 F°-kal lett magasabb. [5]

Mivel a két kaloriméter hőkapacitása egyenlő volt, ez azt jelenti, hogy ha a mechanikai egyensúly után sok­kal lassabban beáll majd a termikus egyensúly is a két edényben levő gáz között, akkor a véghőmérséklet a mérési pontosságon belül meg kell hogy egyezzék a kiin­dulási hőmérséklettel.

Joule körültekintő kísérletező ügyessége tette lehetővé, hogy a Gay-Lussac kísérlet visszanyerte eredeti bizonyító erejét. Már csak egyedül Joule nem volt megelégedve a mérési pontossággal. Az az igazság, hogy Joule, amikor eredeti formájában - tehát egyetlen közös kaloriméter­ben - ismételte meg Gay-Lussac kísérletét, mégiscsak kapott valamennyi hőmérsékletváltozást, de ez a mérési hiba határát súrolta.

Azóta, hogy 1807-ben Gay-Lussac megfogalmazta nevezetes tételeit a gázok egyenlő viselkedéséről a kísér­leti módszerek finomodásával egyre több kételkedő kutató lépett fel Gay-Lussac kijelentését cáfoló mérési adatokkal. A Francia Akadémia már 1811-ben pályázatot hirdetett a minél pontosabb kísérleti vizsgálatokra. Joule-ban két nézet viaskodott egymással. Egyik a gázok egyforma viselkedését értelmezni tudó molekuláris elmé­let kidolgozásának reménye, amely szerint CV állandó. Másik a saját és mások kísérletei alapján felmerülő kétely CV állandóságában. Hogyan növelhető a fajhőmé­rések pontossága?

Joule 1848-ban, Manchesterben egy tudományos felolvasóülésen kifejti azt a véleményét, hogy "azok a kutatá­sok, melyeket Victor Regneault a francia kormány megbízásából vállalt a testek hőkapacitásának fontos problémáját is felölelik, így rövid időn belül új meghatározást várhatunk a gázok fajhőjére. Ezt a meghatározást ugyanaz a pontosság fogja jellemezni, amely teljesen megérdemelten szerzett dicsőséget ennek a híres kutató­nak." [6]

Ennél a híres kutatónál dolgozott néhány hónapig 1845-ben, miután Cambridge-ben matematikából és fizi­kából diplomázott - William Thomson. A Regnault által követelt nagy mérési pontosság indította Thomsont azokra a vizsgálatokra, amelyek az abszolút hőmérsékleti skála felállításához vezettek. Megszületett a tökéletes gáz absztrakciója, melyet a valódi gázok csak több-kevesebb pontossággal közelítenek. Itt Párizsban ásta ki a jótékony(?) feledés süllyesztőjéből a 21 éves Thomson az akkor már 13 éve halott Carnot-nak 1824-ben (Thomson születésének évében) publikált dolgozatát, és hazatérve Glasgowba 1848-ban közölte a termodinamikai hatásfokra alapozott abszolút hőmérsékleti skálát.

Glasgow és Manchester mintegy 300 km-re vannak egymástól. Thomson és Joule szelleme számára ennél nagyobb távolság sem lett volna akadály barátságuk kialakulásához. Joule hat évvel volt idősebb Thomsonnál, először 1847-ben találkoztak [7]; lehet, hogy éppen Thomson hívta fel Joule figyelmét Regnault pontos méréseire.

Ettől kezdve állandó levelezésben álltak egymással. Ha Thomson egyetemi előadásán valami új, frappáns demonstrációs kísérletet talált ki, azonnal megírta Joule-nak. Ugyanakkor Thomsont, akit lenyűgözött Fourier munkássága, amely még a hőanyag modelljével írta le matematikailag a hővezetés elméletét, egyedül Joule kísérleti eredményei győzték meg a hőanyagelmélet tarthatatlanságáról. [7, 8]

Közös munkájuk legszebb eredménye annak az effek­tusnak a felfedezése, mellyel ipari méretekben megindul­hatott a gázok cseppfolyósítása, s amely ma valamennyi háztartási hűtőgép működésének egyik nélkülözhetetlen feltétele, az un. Joule-Thomson effektus.

3. A Joule-Thomson-kísérlet

Vegyünk egy hőszigetelt falú hengert, melyet középen egy porózus anyagból készült fal (pl. vattadugó) választ két részre (3. ábra).

3. ábra

3. ábra

A henger két oldalán 1-1 adiabatikus dugattyút mozgatunk úgy, hogy a porózus fal két oldalán a nyomás állandóan p1 illetve p2 maradjon, miközben a porózus falon keresztül a gáz lassan áramlik a nagyobb nyomású oldalról a kisebb nyomású oldalra. (A porózus fal szerepe az, hogy ugyan megengedi a gáz átáramlását, de nem engedi a gázt felgyorsulni. Mintegy "lefojtja" a gáz áram­lását, ezért a kísérletet gyakran "fojtásos" kísérletnek is nevezik. A fojtás szerepét egy szűkület is átveheti a cső­ben, a gyakorlati alkalmazás során gyakran így valósítják meg az effektust.)

A porózus fal két oldalán termoelemekkel mérjük a T1 és T2 hőmérsékleteket.

A kísérlet irreverzibilis, bár a gáz kezdő és végállapota (amikor csak a baloldalon illetve csak a jobboldalon helyezkedik el a kiszemelt gázmennyiség) egyensúlyi állapot.

Ezt az alábbi ábrákkal lehet szemléltetni (4. ábra).

Állítás: U1+ p1Vl = U2 + p2V2

Bizonyítás: Az első főtétel értelmében

U2 - U1= Q + W

Most Q = 0 az adiabatikus szigetelés miatt,

W = p1V1 - p2V2 mert a baloldali dugattyú lenyomásakor p1V1 munkát végzünk, a jobboldali dugattyú elmozdulása közben pedig p2V2 munkát nyerünk. A befektetett munka így a kettő különbsége.

Átrendezés után kapjuk a bizonyítandó állítást.

A H = U + pV mennyiséget entalpiának nevezzük, így a Joule-Thomson kísérletben

H1 = H2

4. ábra
4. ábra

mindig, akármilyen gázzal végezzük is azt el. A gáz új egyensúlyi állapota tehát mindig ugyanolyan entalpiájú, mint a kiindulási állapot volt.

Ideális gázra pV = RT, tehát U = H - RT, vagyis ez a kísérlet ugyanúgy alkalmas annak az igazolására, hogy a belső energia csak a hőmérséklet függvénye, mint a Gay-Lussac kísérlet. Ha pedig T a második főtétellel definiált abszolút hőmérsékletet jelenti, akkor a Gay­-Lussac kísérlethez hasonlóan ez is alkalmas lesz az abszolút hőmérsékleti skála és az ideális gáz hőmérsékleti skála egyenértékűségének bizonyítására, s közvetve a második főtételbe vetett bizalmunk megerősítésére.

Csupán azt kell a méréssel ellenőriznünk, igaz-e, hogy T1= T2.

Viszont óriási különbség van a Gay-Lussac kísérlet és a Joule-Thomson kísérlet mérési megbízhatósága, pontossága között!

Itt közvetlenül a gáz hőmérsékletét mérjük a kis hőkapacitású termoelemekkel, ezért a hőmérsékletmérés pontossága legalább egy nagyságrenddel nagyobb.

Másrészt a Joule-Thomson kísérletben nem egy meghatározott, korlátozott tömegű gáz állapotváltozását vagyunk kénytelenek megvizsgálni, mint a Gay-Lussac kísérletben, hanem megfelelő kompresszort és nyomás­szabályozókat csatlakoztatva a henger két oldalára, a nyomásokat szabályozottan állandó értékeken tudjuk tartani, s így tetszőleges mennyiségű gáz állapotváltozá­sát tudjuk figyelemmel kísérni. A Joule-Thomson kísér­let során kivárhatjuk a stacionárius (időben állandó) folyamat kialakulását. Az egyetlen probléma a jó hőszi­getelés megvalósítása, az ebből eredő hiba csökkentésére helyezzük el a termoelemeket a fojtás közelében.

Mivel a Joule-Thomson kísérlet is olyan irreverzibilis folyamat, ahol a kezdő és végállapot egyensúlyi, ezért itt is kiszámítható az entrópianövekedés, a Gay-Lussac kísérlethez hasonló módon.

Tekintsünk egy egyensúlyi, izentalpikus folyamatot: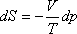
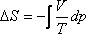
TdS = dU + pdV
TdS = d(U + pV) - Vdp
TdS = dH - Vdp
dH = 0, tehát
TdS = -Vdp
képlet
képlet

Mivel a Joule-Thomson kísérletben p2 < p1, ezért a helyettesítő egyensúlyi folyamatban

dp < 0.

kell, hogy legyen. Tekintettel arra, hogy V > 0, és T > 0, ezért szükségképpen

ΔS > 0.

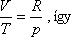
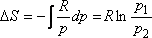
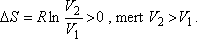
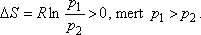
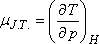
Egy mól ideális gázra   képlet

képlet

Az egyensúlyi folyamat során ugyanennyivel csökken a folyamatban résztvevő hőtartályok összentrópiája, viszont az irreverzibilis Joule-Thomson kísérletben ez a kompenzáló entrópiacsökkenés hiányzik, mivel a gáz környezettől adiabatikusan el van szigetelve.

Hasonlítsuk össze egy mól ideális gáz entrópiaváltozá­sát a két kísérletben!

Gay-Lussac kísérlet:

képlet

Joule -Thomson-kísérlet:

képlet

A Gay-Lussac kísérletben V2 / V1 = 2 volt, a Joule­-Thomson kísérletben azonban p1 / p2 = 200 is lehet!

Reális gázok esetén is sokkal nagyobb a tömegegységre jutó entrópianövekedés a Joule-Thomson kísérletben, mint a Gay-Lussac kísérletben. Ez is oka annak, hogy a reális gázok esetén mérhető hőmérsékletváltozás sokkal nagyobb a Joule-Thomson kísérletben, mint a Gay­Lussac kísérletben.

Hőmérsékletváltozások a Joule-Thomson-effektus során

Ha 200 atm-ról 1 atm-ra csökkentjük az eredetileg 52 °C-os levegő nyomását, akkor hőmérséklete 23 °C-ra csökken. Ha 52 °C-os hélium nyomását csökkentjük 200 atm-ról 1 atm-ra, akkor a hélium 64 °C-ra melegszik fel. Tipikus hűtőközegek az ammónia és a freon 12. Ha ezek hőmérsékletét akarjuk 30 °C-ról -15 °C-ra csökken­teni a Joule-Thomson effektus segítségével, akkor az ammónia nyomását például 12 atm-ról 2,4 atm-ra, a freon 12 nyomását pedig elég 7 atm-ról 1,8 atm-ra csökkenteni.

Általánosan jellemző kísérleti tapasztalat, hogy a kritikus nyomásnál legalább egy nagyságrenddel nagyobb kezdőnyomásról indulva mind hőmérsékletcsökkenés, mind hőmérsékletemelkedés lehetséges a Joule-Thomson kísérletben. Ez csak attól függ, hogy milyen a végállapot­beli nyomás. Kivételt képeznek azonban például az igen magas hőmérsékletű kezdőállapotok, ekkor a Joule­-Thomson effektus mindig a hőmérséklet emelkedéséhez vezet.

Példaképpen nézzük meg a túlhevített vízgőz esetét. Ennek kritikus hőmérséklete 374 °C = 647 K, kritikus nyomása 225 atm. A mérnöki gyakorlatban használatos vízgőztáblázatokból kiolvasható, hogy ha mondjuk 2 atm-ról 1 atm-ra fojtjuk le a túlhevített vízgőz nyomását Joule-Thomson-effektus segítségével, akkor 130 °C-ról indulva 4,5 °C-os hőmérsékletcsökkenést, 165 °C-ról in­dulva 3 °C-os csökkenést, 500 °C-ról indulva 0,5 °C-os csökkenést kapunk. Ahhoz, hogy a hőmérséklet ne csökkenjen, hanem emelkedjék, a kiindulási hőmérsékletet jóval 1000 °C fölé kellene emelni. Olyan magasra amikor viszont a H2O molekulák a nagy sebességű ütközések következtében részben gerjesztődnének, esetleg ionizálódhatnak is, s ekkor már nem az eredeti gázról lenne szó. A mérnöki vízgőztáblázatokban nem is találunk 1000 °C­-nál nagyobb hőmérséklethez tartozó adatokat.

A Joule-Thomson-effektus adta hőmérsékletváltozás azonban nem csak a kiindulási hőmérséklettől, hanem a kiindulási nyomástól is függ. Ha például az 500 °C-os vízgőz nyomását nem 2 atm-ról fojtjuk le 1 atm-ra, hanem 500 atm-ról 499 atm-ra, a hőmérsékletcsökkenés az előbbi 0,5 °C-nak is csak a fele, 0,25 °C lesz. Ez azt mutatja, hogy elég magas nyomáson az ilyen kis Δp értékkel való fojtás (ezt nevezik differenciális Joule­-Thomson effektusnak) előbb-utóbb hőmérsékletemelke­déshez vezet.

Persze ha az 500 °C-os, 500 atm nyomású vízgőz nyomását 1 atm-ra fojtjuk, (ez az igazi, vagy "integrális" Joule-Thomson effektus) akkor hőmérséklete már jelentősen csökken, lehűl 122 °C-ra).

Nemcsak gázzal, hanem folyadékkal is elvégezhetjük a Joule-Thomson kísérletet. A H2O példájánál maradva megvizsgálhatjuk, hogyan változik a víz hőmérséklete a fojtásos folyamat során. A víz entalpiája elég jó közelítésben csak a hőmérséklet függvénye, így csak nagyon kis hőmérsékletváltozásokat várhatunk. Induljunk ki itt is az 500 atm nyomású kezdőállapotból, legyen a kezdő­hőmérséklet 273 °C (= 546 K). Ha követjük azt a izentalp görbét, amely ezen a kezdőállapoton halad át a p; T diagramon, akkor az alábbi p, T értékpárokhoz jutunk:

p; 500 atm    400 atm     300 atm     200 atm     100 atm
T; 273,0 °C   273,2 °C    273,4 °C   273,3 °C   272,8 °C

Ez azt jelenti, hogy ha az 500 atm nyomású 273 °C hőmérsékletű H2O fluidumot 400 atm-ra fojtjuk, akkor 0,2 °C-kal felmelegszik, ha viszont 100 atm-ra fojtjuk, akkor 0,2 °C-kal lehűl. Ha éppen 125 atm-ra fojtanánk, hőmérséklete pontosan ugyanannyi lenne, mint a kiindu­lási állapotban volt.

Nemcsak ideális gázra jellemző tehát, hogy a Joule-Thomson folyamatban nincs hőmérsékletváltozás.

Minden tiszta anyagra, nem túl kicsi és nem túl nagy hőmérsékletek esetén akármelyik hőmérséklethez tarto­zik tetszőlegesen sok olyan (p, p') nyomás értékpár, amelyek entalpiája egyenlő egymással.

Ekkor a nagyobb nyomásról a megfelelő kisebb nyo­másra fojtva az anyagot, hőmérséklete nem változik meg. Az előbb említett 273 °C vizet 500 atm-ról 125 atm-ra, vagy 400 atm-ról 175 atm-ra vagy 350 atm-ról 250 atm-ra fojtva nem lesz hőmérsékletváltozás. A differenciális Joule-Thomson effektus során ezen a hőmérsékleten kb. 300 atm nyomáson nem lesz hőmérsékletváltozás.

Joule-Thomson koefficiens

A víz most leírt viselkedése a tiszta anyagokra általá­ban is jellemző, s az alábbi ábrákon foglalható össze: (5. ábra.).

A p; T koordinátarendszerben az olyan p*, T* állapot, amely esetén a differenciális Joule-Thomson-effektus­ban nincs hőmérsékletváltozás, mindig egy izentalp görbének a legnagyobb hőmérsékletű állapota. Látszik, hogy ugyanilyen entalpiájú, de p*-nál kisebb nyomású állapotok esetén differenciális Joule-Thomson-effektus során a hőmérséklet csökken, p*-nál nagyobb nyomások esetén nő. Ezért a p*, T* állapotot a megfelelő entalpiához tartozó "inverziós állapotnak" hívják, itt "fordul meg" (invertálódik) a differenciális Joule-Thomson-­effektus kimenetele.

A differenciális Joule-Thomson-effektus eredményé­nek mennyiségi jellemzésére vezették be az ún. Joule­Thomson-koefficienst (µJ.T.,) az alábbi definícióval:

képlet

Az egyensúlyi termodinamika alapösszefüggései segít­ségével µJ.T.-t az anyag más jellemzőivel is összekapcsol­hatjuk:

TdS = dU + pdV
TdS = d(U + pV) - Vdp
TdS = dH -Vdp

5. ábra

5. ábra. Állandó entalpiájú (izentalp) görbék és fojtásos folyamatok ábrázolása a (p; T) koordinátarendszerben
5. a. ábra. A kezdeti (pk, Tk) állapotból melegebb (p1, T1) és hidegebb (p2, T2) állapotba is átmehet az anyag. Ha nyomását éppen p3-ra csökkentjük, hőmérséklete nem változik.
5. b. ábra. Ugyanahhoz a hőmérséklethez tetszőleges sok olyan (pi, pi') nyomás értékpár tartozik, amelyek esetén nem lesz hőmérsékletváltozás a Joule-Thomson-kísérletben.
5. c. ábra. Egy kiválasztott T* hőmérséklethez tartozó p* nyomás, amely esetén a differenciális Joule-Thomson effektusban nem lesz hőmérsékletváltozás

Legyenek az extenzív állapotjelzők (S, H, V) p és T függvényei. Ekkor S = S (p,T) teljes differenciálja:

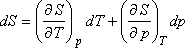
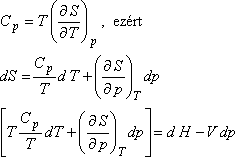
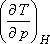képlet

Másrészt

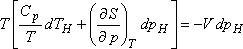
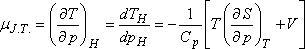
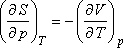
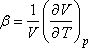
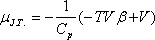
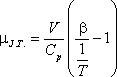
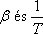képlet

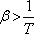Tekintsük azt a speciális esetet, amikor dH = 0, mivel képlet-t akarjuk meghatározni:

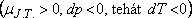képlet

Ebből az egyenletből:

képlet

Szemléletesebb kifejezést kapunk, ha felhasználjuk a következő Maxwell relációt:

képlet

valamint a térfogati hőtágulási együttható alábbi definí­cióját:

képlet

Ezekkel

képlet

ami így is írható:

képlet

A most levezetett összefüggésünk alapján a Joule-­Thomson-koefficiens előjelét képlet viszonyával tudjuk összekapcsolni.

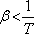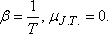Az anyagnak azokban az állapotaiban, ahol képlet a Joule-Thomson-koefficiens pozitív, tehát a differenciális Joule-Thomson-effektus során az anyag hőmérséklete csökken. képlet Ha viszont képlet, akkor az anyag melegszik. Abban az esetben, amikor képlet. Ez éppen az ideális gáz esetén valósul meg, hiszen az ideális gázra

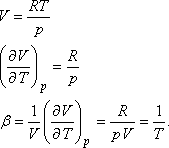
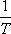képlet

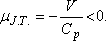
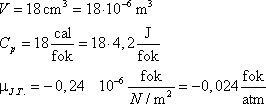
Térjünk vissza a víz példájához. A víz hőtágulási együtthatója képlet-hez képest rendkívül kicsi (0 °C és 4 °C között negatív, 4 °C-on zérus, 4 °C és 100 °C között pozi­tív - 1 atm nyomáson), ezért jó közelítésben a Joule­Thomson koefficiens vízre:

képlet

Vagyis a víznek melegednie kell a fojtásos folyamatban. Behelyettesítve a mólnyi mennyiségű vízre jellemző adatokat:

képlet

A várható hőmérsékletemelkedés 1000 atm nyomásesés esetén 24 °C. Ez a becslés jól egyezik a víz-vízgőz táblá­zatokból kiolvasható értékkel.

Felmerül a kérdés: a szokásos, szobahőmérsékletű víznek nincs inverziós pontja? Miért mindig csak meleg­szik a Joule-Thomson-effektus során?

Említettük, hogy az inverziós állapot minden tiszta anyagra így H2O-ra is csak nem túl kicsi és nem túl nagy hőmérsékleteken léphet fel. Ez a hőmérsékletintervallum nagyon tág, és általában a hármasponti és a kritikus hőmérséklet közötti értéktől a kritikus (abszolút) hőmér­séklet többszöröséig tart. Vízre az alsó határ 234 °C körül van (kb. 507 K). Ennél alacsonyabb hőmérsékleteken a folyadék víz csak melegszik a fojtásos folyamatban.

Az inverziós görbe

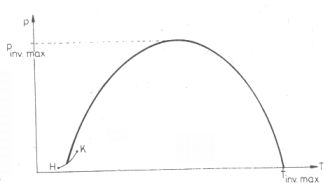
Az inverziós állapotokat ábrázoló pontok a p;T koor­dinátarendszerben egy maximummal rendelkező görbén helyezkednek el, amely valahol a folyadék-gőz fázishatár görbéről indul jóval a kritikus hőmérséklet után éri el újra a T tengelyt (6. ábra). Ezt az utóbbi határhőmér­sékletet, amely a lehetséges legnagyobb inverziós hőmér­séklet nevezik gyakran egyszerűen inverziós hőmérsék­letnek. Fontos jelentése van: ha Joule-Thomson effek­tussal hőmérsékletcsökkenést szeretnénk elérni, akkor az anyag kiindulási hőmérsékletének ennél kisebbnek kell lennie. H2O esetén persze ez egy olyan óriási hőmérséklet, hogy a kérdés feltevése se indokolt. Az inverziós hőmérséklet levegő esetén még 330 °C, hidrogén és különösen hélium esetén azonban jóval a szobahőmérséklet alatt van. Hidrogénre -71 °C = 202 K, ami a hidrogén kritikus hőmérsékletének (33,3 K-nak) még mindig kb. a hatszorosa. Nitrogénre a maximális inverziós hőmérsék­let a kritikus hőmérséklet ötszöröse, héliumra pedig 7,7-szerese (kb. 40 K).

6. ábra
6. ábra. Inverziós görbe a (p; T) koordinátarendszerben. H = Hármaspont (a gáz, a folyadék és a szilárd fázis közös egyensúlyi állapota), K = Kritikus pont (a H-t K-val összekötő, ún. folyadék-gáz fázishatárgörbén vannak a telített gőz állapotok)

Tinv.max. = a legnagyobb inverziós hőmérséklet
pinv.max. = a legnagyobb inverziós nyomás

Az inverziós görbe alatti tartományban µJ.T. > 0, az inverziós görbén µJ.T. = 0, felette pedig µJ.T. < 0.

A folyadék-gáz fázisgörbe alatt a Joule-Thomson-­ koefficiens pozitív, tehát pl. a vízgőzt 234 °C hőmérséklet alatt is lehet hűteni Joule-Thomson-effektussal. (234 °C-­on és 30 atm nyomáson éri el H2O esetén az inverziós görbe a víz-vízgőz fázishatárgörbét). A 10 atm-ás 190 °C hőmérsékletű vízgőz hőmérséklete 163 °C-ra csökken, ha fojtással a nyomását 1 atm-ra csökkentjük. A 2 atm-ás 120°°C-os vízgőz hőmérséklete 111 °C-ra csökken, ha 1 atm-ra tágul ki a fojtásos folyamatban (kuktafazék szelepén kiáramló eset), az 1 atm-ás 100 °C-os vízgőzt 0,01 atm-ra fojtva pedig 93 °C lesz a hőmérséklete.

Ha összehasonlítjuk különböző gázok inverziós hőmér­sékleteinek mért értékeit, ez ugyanolyan nagy változatos­ságot mutat, mint amilyen változatosak a kritikus hőmérséklet mért értékei. A kettő hányadosa azonban már sokkal kevésbé változik. Tájékozódásul álljon itt néhányjellemző adat: [9]


TkrTinv.max Tinv.max/Tkr
N2  126 K 621 K4,9
levegő  132 K 603 K4,6
Ar  151 K 723 K4,8
H2 33,3 K 202 K6,1
He  5,2 K  40 K7,7


pkrpinv.max pinv.max/pkr
N233,5 atm 400 atm12
H212,8 atm 106 atm13
He 2,3 atm 37 atm16

A fenti táblázatban nemcsak a maximális inverziós hőmérsékletet, hanem az inverziós görbe maximumához tartozó nyomást is összehasonlítottuk a kritikus állapot­hoz tartozó megfelelő értékekkel.

Érdemes ezek után megnézni, hogy a reális gázokra leggyakrabban használt állapotegyenletek - melyeket molekuláris fizikai meggondolásokból kaphatunk ­mennyire jól adják ezeket az értékeket. A legismertebb ilyen állapotegyenlet a van der Waals állapotegyenlet:

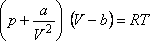
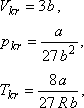
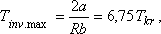
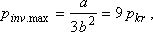
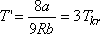
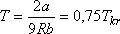képlet

Az ebben szereplő a, b, R paraméterekkel a kritikus térfogat, nyomás és hőmérséklet az alábbi módon fejez­hető ki (l. pl. [10]):

képlet

Mint azt az alábbiakban meg fogjuk mutatni, a van der Waals állapotegyenlet valóban egy maximummal rendel­kező inverziós görbét szolgáltat, ahol a maximális inver­ziós hőmérséklet:

képlet

és a maximális inverziós nyomás:

képlet

Ezt a maximális értéket az inverziós görbe a

képlet

hőmérséklet esetén éri el.

Érdekes még a van der Waals inverziós görbe másik metszéspontja a T tengellyel. Ez nem T" = 0-nál van, hanem képlet-nál. (Emlékezzünk vissza, hogy H2O esetén a mérési adatok szerint az inverziós görbe 507 K-nél metszi a folyadék-gőz fázishatárgörbét. Ez a H2O kritikus hőmérsékletének - 647 K-nek ­0,78-szorosa).

Összehasonlítva a van der Waals állapotegyenlet által jósolt

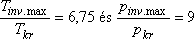
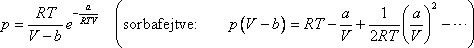
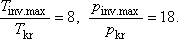
képlet

értékeket a fenti táblázat mérési adataiból számolt hányadosok megfelelő értékeivel, azt mondhatjuk, hogy a van der Waals állapotegyenlet viszonylag jól jelzi az inverziós görbe menetét.

Hélium esetén még jobb egyezést kapunk, ha a reális gázok Dieterici féle állapotegyenletét használjuk. Ez 1 mólra az alábbi alakú [11, 12]:

képlet

Ha itt is kifejezzük a kritikus adatokat a Dieterici féle a, b állandókkal és R-rel, valamint meghatározzuk a µJ.T. = 0-hoz tartozó görbét akkor a megfelelő hánya­dosokra az alábbiakat kapjuk:

képlet

Határozzuk most meg az inverziós görbe egyenletét van der Waals gázra!

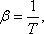Ehhez képlet kell meghatároznunk, mivel µJ.T. = 0, ha képlet, vagyis képlet

A van der Waals állapotegyenlet:

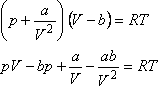
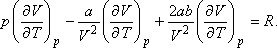
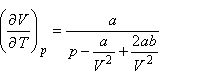
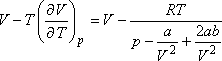
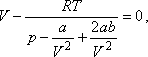
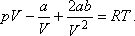
képlet

Differenciáljuk ezt parciálisan a hőmérséklet szerint, állandó nyomás mellett:

képlet

Innen

képlet

képlet

A Joule-Thomson-koefficiens tehát akkor lesz zérus, ha

képlet

amit átalakítva így is írhatunk:

képlet

Ez a feltételi egyenlet az állapotegyenlettel együtt az inverziós görbe V paraméteres megadásának tekint­hető a p;T koordinátarendszerben. A két egyenletből

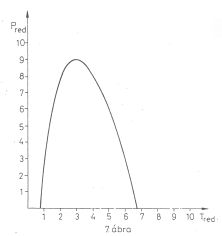
7. ábra
7. ábra A Van der Waals gáz inverziós görbéje;

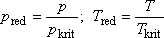
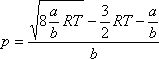
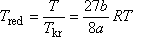
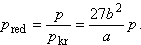
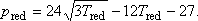
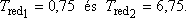
képlet

ügyes matematikai átalakítások segítségével V kiküszö­bölésével megkaphatjuk az inverziós görbét leíró p(T) függ­vény explicit kifejezését is. Ez a következő:

képlet

Még áttekinthetőbb és érdekesebb lesz ez a kifejezés, ha az állapotjelzők redukált értékeire írjuk fel. Tekintettel arra, hogy

képlet

és

képlet

van der Waals gáz esetén, a következőt kapjuk:

képlet

Ennek a függvénynek a zérushelyei:

képlet

Maximumhelye: Tred.max = 3-nál van, a maximál nyomás redukált értéke itt:

pred.max = 9

. A van der Waals inverziós görbe menete a 7. ábrán látható. Gyakorlati alkalmazások A múlt század utolsó évtizedeiben a gázok cseppfolyó­sításának nagyszabású programja többek között. éppen a Joule-Thomson-effektus felfedezése nyomán bonta­kozhatott ki.

Ugyancsak a Joule-Thomson-effektust használják fel napjakban az ipari és háztartási hűtőgépekben, vala­mint a légkondicionáló berendezésekben.

Mindezek tárgyalása azonban már meghaladná e cikk kereteit, a gyakorlati alkalmazások témája külön tanul­mányt érdemel.

IRODALOM

 [1] Radnai Gyula: Egyszerű rendszerek állapotegyen­letei, ELTE TTK. Szakmódszertani Közlemények X. 13-37. o. (1977).
[2] Radnai Gyula: Egyszerű rendszerek egyensúlyi állapota és a termodinamikai állapotfelület, Fizikai Szemle XVIII. 223-237. o. (1978).
[3] Czógler Alajos: A fizika története életrajzokban, Természettudományi Könyvkiadó Vállalat, Buda­pest (1882) II. kötet; 97. o.
[4] Gay-Lussac, J. L.: Memoire sur la dilatation des gaz et des vapeurs, Ann. de Chimie, XLIII. (1802).
[5] Kudrjavcev, P. Sz.: A fizika története, Akadémiai Kiadó, Budapest (1951) 490. o.
[6] Kudrjavcev, P. Sz.: A fizika története, Akadémiai Kiadó, Budapest (1951) 555. o.
[7] Simonyi Károly: A fizika kultúrtörténete, Gondolat Kiadó, Budapest (1978) 314. o.
[8] Mac Donald: Faraday, Maxwell and Kelvin, Doubleday Anchor Books, New York (1964) 114. o.
[9]Zemansky, M. W.: Heat and Thermodynamics, Mc Graw-Hill Book Co., New York (1968) 340. o.
[10] Budó Ágoston, Pócza Jeno: Kísérleti fizika I. Tan­könyvkiadó, Budapest (1962) 456. o.
[11] Parsonage, N. G.: The Gaseous State, Pergamon Press, London (1966) 26. o.
[12] Kubo, R.: Thermodynamics, North-Holland Publ. Co. Amsterdam (1968) 125. 0.