Fizikai Szemle 1960/11. 337.o.
Fényhullámok dinamikájáról
Györgyi Géza
Newton, a fény általa felállított részecskeelméletében, - amint az jól ismeretes - a következő gondolatmenet alapján kísérelte
meg a fénytörés jelenségének értelmezését. Tegyük fel, hogy egy törőközeg sík határfelületét a beeső "fényrészecskék"
párhuzamos nyalábja éri. Jelöljük egy fényrészecske impulzusát a vákuumban P0-lal, a közegbe való
behatolás után pedig P-vel. Newton feltette, hogy a fényrészecskékre a törőközeg felületén az n belső normálissal
párhuzamos erő hat. Ez az erő a fényrészecske impulzusának n-nel párhuzamos összetevőjét változtatja meg; az n-re
merőleges összetevőt változatlanul hagyja:
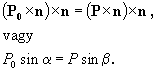 | (1) |
Itt a az n és P0, 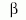 pedig az n és P vektorok közbezárt
szögét jelöli. Newton feltételezte, hogy a P0 és P impulzusok, valamint a megfelelő sebességek
között a részecskék mechanikájából ismert alakú összefüggések állnak fenn:
pedig az n és P vektorok közbezárt
szögét jelöli. Newton feltételezte, hogy a P0 és P impulzusok, valamint a megfelelő sebességek
között a részecskék mechanikájából ismert alakú összefüggések állnak fenn:
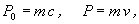 | (2) |
ahol c és v a vákuumbeli, ill. a közegbeli fénysebességet jelöli, m pedig a fényrészecske tömegét.
Az (1-2) egyerletekből m, valamintP / P0 kiküszöbölése útján a Snellius-Descartes-féle törési
törvényt kapjuk:
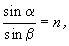 | (3) |
ahol
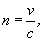 | (4) |
A közegbeli v fénysebesség közvetlen meghatározására végzett mérésekből azonban kiderült, hogy a (4) egyenlet
nem helyes. A szereplő mennyiségek között ehelyett a következő összefüggés áll fenn:
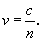 | (5) |
A fény hullámelméletének általános sikere után a fenti okoskodást, melyben fényrészecskékre történik hivatkozás, - úgy
vélhetnénk - teljes egészében el kell vetnünk. A következőkben azonban látni fogjuk, hogy a fényhullámok (hullámcsomagok)
dinamikai viselkedését figyelemmel kísérve, a fenti okoskodáshoz bizonyos fokig hasonló módon, a fénytörés törvényére
dinamikai magyarázatot adhatunk.
Most következő megfontolásaink azért is érdeklődésre tarthatnak számot, minthogy összefüggenek azzal a több mint fél évszázados
vitával, mely akörül folyik, vajon Abraham vagy Minkowski energia-impulzustenzora tükrözi hívebben az elektromágneses tér
dinamikai viselkedését polározható közegben. A két energiaimpulzus-tenzor különbözősége lényegében annak folyománya, hogy
Abraham, ill. Minkowski eltérő kifejezéseket javasoltak az elektromágneses tér polározható közegben érvényes impulzussűrűségére.
Max Abraham azt a feltevést tette, hogy az elektromágneses tér G impulzussűrűsége a törőközeg belsejében
az E elektromos és a H mágneses térerősségnek ugyanolyan alakú kifejezése, mint vákuumban:
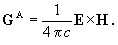 | (6) |
Hermann Minkowski ehelyett egy más kifejezést javasolt, mely az előbbitől az 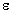 µ szorzóban különbözik:
µ szorzóban különbözik:
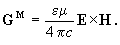 | (7) |
Itt 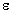 a dielektromos állandó, µ a mágneses permeabilitás; feltételezzük, hogy a közeg homogén, izotróp és nemdiszpergáló.
Síkhullám esetén (6)-ból a következő kapcsolat adódik a G impulzussűrűség, az
u = (E2 + H2) / 8
a dielektromos állandó, µ a mágneses permeabilitás; feltételezzük, hogy a közeg homogén, izotróp és nemdiszpergáló.
Síkhullám esetén (6)-ból a következő kapcsolat adódik a G impulzussűrűség, az
u = (E2 + H2) / 8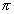 energiasűrűség, valamint a v terjedési
sebesség között
energiasűrűség, valamint a v terjedési
sebesség között 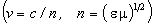 :
:
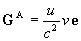 | (6a) |
Ha viszont (7)-et vesszük alapul, ehelyett a
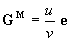 | (7a) |
összefüggésre jutunk. (e a terjedési irányba mutató egységvektort jelöli.)
Vegyünk szemügyre most egy hullámcsomagot, mely kiterjedésén belül jó közelítésben síkhullámnak tekinthető. Írjuk
fel e hullámcsomag P = 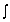 G dV impulzusának és
E =
G dV impulzusának és
E = 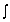 u dV energiájának kapcsolatát. (Itt
u dV energiájának kapcsolatát. (Itt 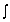 . . . dV
a hullámcsomag által elfoglalt térfogatra kiterjesztett integrálást jelöl.) (6a) alapján e kapcsolat a
. . . dV
a hullámcsomag által elfoglalt térfogatra kiterjesztett integrálást jelöl.) (6a) alapján e kapcsolat a
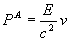 | (6b) |
alakúnak adódik, ha viszont (7a)-t vesszük alapul,
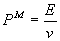 | (7b) |
összefüggésre jutunk. Vákuumban természetesen mind Abraham, mind Minkowski feltevése alapján ugyanazt az eredményt kapjuk:
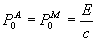 | (8) |
Eredményeink birtokában azt gondolhatnánk, hogy a fénytörés jelenségével kapcsolatban a következőképpen érvelhetünk1,2.
Az Abraham feltevése alapján kapott (6b), (8) egyenletek P és v, ill. c között (2)-vel analóg alakú
kapcsolatot létesítenek; a fényrészecske m tömegének szerepét a hullámcsomag E energiájához tartozó
E / c2 tömeg veszi át - összhangban az energia tehetetlenségének Einstein-Planck-féle törvényével.
A (2) egyenletek alapján azonban a helytelennek bizonyult (4) összefüggésre jutottunk. - Ugyanakkor a Minkowski feltevése
alapján kapott (7b) egyenlet nem áll összhangban a Planck-Einstein-tétellel. Mindazonáltal, ha az (1) egyenletbe az impulzus
Minkowski szerint érvényes (7b), (8) értékeit helyettesítjük, a Snellius-Descartes-törvény mellett megkapjuk a, v terjedési
sebesség és az n törésmutató kapcsolatát helyesen kifejező (5) összefüggést.
Érvelésünk - úgy látszhat - azt az eredményt adta, hogy a térimpulzus sűrűségének csupán (7) alatti, Minkowski-féle
definíciója van összhangban a fénytörésre és a fény törőközegbeli sebességére vonatkozó tapasztalati tényekkel.
Gondosabb vizsgálattal azonban meggyőződhetünk róla, hogy a bemutatott érvelés meg nem engedett lépést tartalmaz s
így félrevezető. Körültekintőbben eljárva megmutathatjuk, hogy Abraham (6) feltevése alapján ugyancsak lehetséges a
fénytörés kifogástalan elemi dinamikai értelmezése. Sőt, azt találjuk, hogy Minkowski felfogása igen ésszerű és fontos
követelményekkel áll ellentétben., míg Abraham felfogását elfogadva az összhang ezen alapvető követelményekkel megőrizhető.
Az egyik ilyen követelményt, melynek csak az impulzussűrűség (6) alatti Abraham-féle definíciója felel meg, már említettük:
ez az energia tehetetlenségének Einstein-Planck-féle posztulátuma. Egy másik ésszerű követelmény: a tér által a polározható
közegre kifejtett ponderomotoros erő kifejezésének tartalmaznia kell a közegben kialakuló polarizációs áramokra ható
Lorentz-erőt. Amint a következőkben látni fogjuk, a ponderomotoros erősűrűségnek az Abraham-féle feltevés alapján kapott
alakja számot ad erről a jelenségről, a Minkowski-féle erősűrűség viszont nem.
A ponderomotoros erő kifejezése függ attól, hogy milyen alakúnak feltételezzük a térimpulzus sűrűségének kifejezését. Ha
Abraham javaslatát, vagyis az impulzussűrűség (6) alakját fogadjuk el, úgy egy eltűnő mágneses permeabilitású, nemdiszpergáló,
izotróp törőközegben, melyben szabad töltések, valamint vezetési áramok nincsenek jelen, az egységnyi térfogatra ható
ponderomotoros erőre a következő kifejezést kapjuk3:
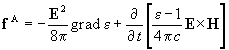 | (9) |
Ha viszont a Minkowski javasolta (7) definíciót fogadjuk el helyesnek, (9) második tagja nem lép fel, s így a ponderomotoros
erősűrűségre a
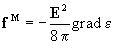 | (10) |
kifejezés adódik.
A törőközegbe behatoló fényhullám impulzusát a közegre kifejtett ponderomotoros erő reakcióereje változtatja meg. A (10) alatti
Minkowski-féle erőképlet megfelel Newton feltételezésének, mely szerint a "fényrészecskére" (melynek helyére
most a hullámcsomag lépett) ható erő merőleges a közeg határfelületére. A (9) alatt felírt Abraham-féle erősűrűségben azonban
az utolsó tag a fény terjedési irányával párhuzamos, s így Newton feltételezése ez esetben nem teljesül. Ha tehát Abraham
felfogását vesszük alapul, az előzőkben alkalmazott gondolatmenetet módosítanunk kell, tekintetbe véve a közegnek átadott
impulzus érintőleges összetevőjét. A behatoló fényhullám a határfelület n normálisára merőleges irányú impulzust
csupán (9) második tagja révén ad át a közegnek (a (9) kifejezés első tagja - éppúgy, mint (10) - n-nel párhuzamos).
Az előzőkben tett feltevéseink alapján a (9) erősűrűség második ta.gját közelítőleg a következő alakba írhatjuk:
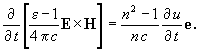 | (11) |
E kifejezést a közeg térfogatára integrálva megkapjuk a közegre ható erőt:
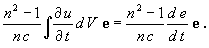 | (12) |
Itt 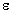 (t) az elektromágneses energiának az a része, mely a t pillanatig a közegbe behatolt. Az átadott impulzust (12) idő
szerinti integrálja szolgáltatja:
(t) az elektromágneses energiának az a része, mely a t pillanatig a közegbe behatolt. Az átadott impulzust (12) idő
szerinti integrálja szolgáltatja:
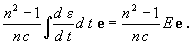 | (13) |
Itt E a közegbe behatolt teljes hullámcsomag energiája.
Eredményünk alapján felírhatjuk a közegnek átadott Pk impulzus n-re merőleges összetevőjét:
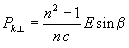
A vákuumból beeső hullámcsomag azon részének n-re merőleges impulzuskomponense, mely a határfelületen visszaverődik,
a visszaverődés során nyilvánvalóan nem változik meg. Ha tehát az impulzus n-re merőleges összetevőjére kívánjuk felírni
a megmaradási törvényt, elegendő a hullámcsomagnak azt a részét tekintetbe vennünk, amely végül behatolt a törőközegbe. A
hullámcsomag ezen részének járuléka az impulzus vákuumbeli értékéhez P0 = E / c. Minthogy
okoskodásunkban Abraham felfogását vettük alapul, a közegbe behatolt hullámcsomag P impulzusára a (6b) képletet kell
használnunk. Írjuk fel most az impulzus megmaradását kifejező egyenletet a 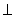 összetevőre:
összetevőre:
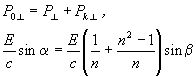
Ez, amint azt egyszerű átalakítással beláthatjuk nem más, mint a (3) törési törvény, és itt n v = c.
Most bemutatott megfontolásaink lehetőséget nyújtanak, hogy fényt derítsünk egy másik problémára, amely Jauchnak és
Watsonnak a polározható közegek kvantumelektrodinamikájára vonatkozó munkájában merült fel.4 E szerzők
a Cserenkov-sugárzással kapcsolatban a következőképpen érvelnek. Az impulzussűrűség (7) Minkowski-féle kifejezését
alapul véve, a részletes megfontolások szerint az adódik, hogy egy törőközegben tovahaladó elektromágneses hullám energiája
a közeghez képest c / n-nél nagyobb sebességgel mozgó vonatkoztatási rendszerben negatív értéket vesz fel.
Ennek a körülménynek Jauch és Watson szerint lényeges szerepe van a Cserenkov-sugárzás értelmezésénél. Vegyünk
szemügyre - e szerzőket követve - egy elektront, amely a közeg belsejében c / n-nél nagyobb sebességgel mozog
(a közeghez képest). Az elektronnal együttmozgó megfigyelő szempontjából a Cserenkov-emisszió folyamata a következőképpen
folyik le. Az emisszió előtt az elektron visszalökődik, s így mozgási energiája zérusról egy pozitív értékre növekszik.
Úgy látszik, hogy az energiamegmaradás tétele csak úgy teljesülhet, ha a kibocsátott hullámcsomag energiája negatív.
Ez a Minkowski-féle felfogás alapján így is van; ugyanakkor meg lehet mutatni, hogy az impulzussűrűség (6) alatti Abraham-féle
kifejezését helyesnek elfogadva, az elektromágneses tér energiasűrűségére határozottan pozitív kifejezés adódik. Jauch és
Watson ezen érvelése alapján úgy látszhat, hogy a Minkowski-féle felfogás az egyedül helyes, az Abraham-féle pedig helytelen
s így elvetendő.
Ez az érvelés azonban a gondosabb vizsgálat fényében nem állja meg a helyét. Ezt a fénytörés esetében alkalmazotthoz hasonló
gondolatmenettel mutathatjuk meg. Az Abraham-féle felfogást alapul véve az energia és impulzus megmaradási tételének
alkalmazásánál a (9) kifejezés második tagját is - melyet Abraham-féle erőnek nevezhetünk - tekintetbe kell vennünk.
Írjuk fel az elektronnak a közeghez rögzített rendszerben érvényes e energiája és p impulzusa között fennálló
relativisztikus összefüggést: e2 = c2 p2 + m2 c4.
Innen a
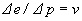 | (14) |
összefüggés adódik az elektron energiájának 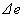 és a mozgásirányba eső impulzuskomponens
és a mozgásirányba eső impulzuskomponens
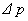 megváltozása
között; itt v = c2 p / e az elektron sebessége. Az impulzusmegmaradás tétele szerint
megváltozása
között; itt v = c2 p / e az elektron sebessége. Az impulzusmegmaradás tétele szerint 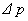 egyenlő a fényhullám által elvitt, (6b) alatt felírt P = E/cn impulzus, valamint a közegnek átadott, (13) alatt
meghatározott [(n2 - 1) / nc] E impulzus negatív előjellel ellátott összegének
cos
egyenlő a fényhullám által elvitt, (6b) alatt felírt P = E/cn impulzus, valamint a közegnek átadott, (13) alatt
meghatározott [(n2 - 1) / nc] E impulzus negatív előjellel ellátott összegének
cos 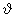 -szorosával. Itt
-szorosával. Itt 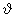 a kibocsátott fényhullám terjedési irányának az elektron (eredeti) mozgásirányával
bezárt szöge. Írható tehát:
a kibocsátott fényhullám terjedési irányának az elektron (eredeti) mozgásirányával
bezárt szöge. Írható tehát:
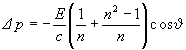
A (14) összefüggést, valamint az energia megmaradását kifejező 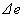 = - E egyenletet felhasználva,
innen a
= - E egyenletet felhasználva,
innen a
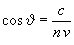
eredményre jutunk. Ez éppen a Cserenkov-sugárzás kibocsátásának irányát megszabó, a megfigyelések által igazolt, jól ismert
képlet. - Eredményünkből természetesen következik, hogy a megmaradási tételek az elektronnal együttmozgó rendszerben is
teljesülnek. Könnyű számítással meggyőződhetünk róla, hogy itt a kibocsátott fény pozitív energiáját, valamint az elektron
visszalökődéskor felvett mozgási energiáját a (rendszerünkben mozgó) közegnek a (12) Abraham-féle erővel szemben végzett
munkája fedezi.5
A fentiekben megbeszélt két jelenség tárgyalása mutatja., hogy a törőközegben haladó fényhullámok viselkedése szempontjából
fontos szerepe van a (12) Abraham-féle erőnek. A következő megfontolásunkban ezen erő fizikai jelentésének megvilágításával
szeretnénk rámutatni: komoly érv szól amellett, hogy Abraham (9) alatti erőtörvényét fogadjuk el helyesnek, a (10)
Minkowski-féle képlettel szemben. - A Lorentz-féle elektronelmélet fényében nem lehet kétségünk afelől, hogy a vezetési áram
és a polarizációs áram között elvi szempontból nem tehető különbség. A helyes erőtörvénynek tehát tartalmaznia kell a
polarizációs áramokra ható Lorentz-féle erősűrűséget:
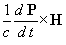 | (15) |
[Itt 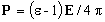 az egységnyi térfogatban foglalt dipólmomentum.]
A (10) alatti Minkowski-féle erősűrűség nyilván nem foglalhatja magában a (15) kifejezést, hiszen (10)-ben sem a mágneses
térerősség, sem pedig időszerinti derivált nem szerepel. A (9) Abraham-féle erőtörvényből ugyanekkor minden külön feltevés
nélkül megkaphatjuk a kívánt (15) tagot. A d H / d t = - c rot E
Maxwell-egyenletet és a
az egységnyi térfogatban foglalt dipólmomentum.]
A (10) alatti Minkowski-féle erősűrűség nyilván nem foglalhatja magában a (15) kifejezést, hiszen (10)-ben sem a mágneses
térerősség, sem pedig időszerinti derivált nem szerepel. A (9) Abraham-féle erőtörvényből ugyanekkor minden külön feltevés
nélkül megkaphatjuk a kívánt (15) tagot. A d H / d t = - c rot E
Maxwell-egyenletet és a
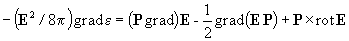
vektoranalitikai azonosságot felhasználva a (9) erősűrűségre a következő új
alakot kapjuk:

Itt az első tag a polarizációs áramra ható Lorentz-erőt leíró, kívánt kifejezés; a második tag pedig az inhomogén erőtérben
dipólusokra ható erősűrűség ismert alakja. A harmadik tag a közeg egész térfogatára integrálva zérus eredőt ad, s
inkompresszibilis közeg esetén az általa végzett teljes munka is zérus. Ez a tag a közeg polarizált állapotának fenntartásával
kapcsolatos és csupán az elektrostrikciós jelenségeknél jut neki lényeges szerep. 6
IRODALOM
- Békéssy A., Freud G., Marx Gy., Nagy K.: Elméleti Fizikai Feladatok. 305. 1. Tankönyvkiadó, Budapest, 1951.
- M. Strauss : Tagungsbericht des I. Intornationalen Kolloquiums der Hochschule für Elektrotechnik, Ilmenau.
- Novobátzky K., Neugebauer T. : Elektrodinamika. Tankönyvkiadó, Budapest, 1950.
- J. M. Jauch, K. M. Watson : Phys. Rev. 74, 950, 1485 (1948).
- Györgyi G. : Magyar Fizikai Folyóirat, 3, 369 (1955).
- Györgyi G. : Magyar Fizikai Folyóirat, 5, 187 (1957).
- G. Marx, G. Györgyi : Acta Phys. Hung. 3, 213 (1954).
- Györgyi G. : Magyar Fizikai Folyóirat, 2, 255 (1954).
________________________________________________
*Megjelent: American Journal of Physics, 28 (1960) 85.
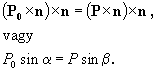
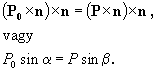
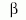 pedig az n és P vektorok közbezárt
szögét jelöli. Newton feltételezte, hogy a P0 és P impulzusok, valamint a megfelelő sebességek
között a részecskék mechanikájából ismert alakú összefüggések állnak fenn:
pedig az n és P vektorok közbezárt
szögét jelöli. Newton feltételezte, hogy a P0 és P impulzusok, valamint a megfelelő sebességek
között a részecskék mechanikájából ismert alakú összefüggések állnak fenn:
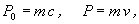
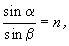
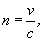
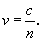
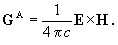
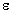 µ szorzóban különbözik:
µ szorzóban különbözik:
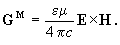
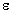 a dielektromos állandó, µ a mágneses permeabilitás; feltételezzük, hogy a közeg homogén, izotróp és nemdiszpergáló.
Síkhullám esetén (6)-ból a következő kapcsolat adódik a G impulzussűrűség, az
u = (E2 + H2) / 8
a dielektromos állandó, µ a mágneses permeabilitás; feltételezzük, hogy a közeg homogén, izotróp és nemdiszpergáló.
Síkhullám esetén (6)-ból a következő kapcsolat adódik a G impulzussűrűség, az
u = (E2 + H2) / 8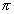 energiasűrűség, valamint a v terjedési
sebesség között
energiasűrűség, valamint a v terjedési
sebesség között 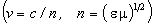 :
:
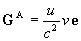
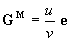
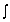 G dV impulzusának és
E =
G dV impulzusának és
E = 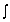 u dV energiájának kapcsolatát. (Itt
u dV energiájának kapcsolatát. (Itt 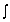 . . . dV
a hullámcsomag által elfoglalt térfogatra kiterjesztett integrálást jelöl.) (6a) alapján e kapcsolat a
. . . dV
a hullámcsomag által elfoglalt térfogatra kiterjesztett integrálást jelöl.) (6a) alapján e kapcsolat a
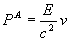
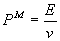
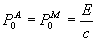
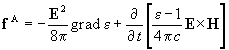
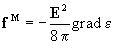
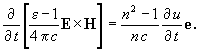
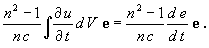
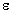 (t) az elektromágneses energiának az a része, mely a t pillanatig a közegbe behatolt. Az átadott impulzust (12) idő
szerinti integrálja szolgáltatja:
(t) az elektromágneses energiának az a része, mely a t pillanatig a közegbe behatolt. Az átadott impulzust (12) idő
szerinti integrálja szolgáltatja:
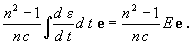
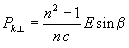
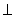 összetevőre:
összetevőre:
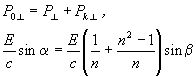
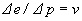
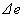 és a mozgásirányba eső impulzuskomponens
és a mozgásirányba eső impulzuskomponens
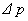 megváltozása
között; itt v = c2 p / e az elektron sebessége. Az impulzusmegmaradás tétele szerint
megváltozása
között; itt v = c2 p / e az elektron sebessége. Az impulzusmegmaradás tétele szerint 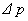 egyenlő a fényhullám által elvitt, (6b) alatt felírt P = E/cn impulzus, valamint a közegnek átadott, (13) alatt
meghatározott [(n2 - 1) / nc] E impulzus negatív előjellel ellátott összegének
cos
egyenlő a fényhullám által elvitt, (6b) alatt felírt P = E/cn impulzus, valamint a közegnek átadott, (13) alatt
meghatározott [(n2 - 1) / nc] E impulzus negatív előjellel ellátott összegének
cos 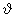 -szorosával. Itt
-szorosával. Itt 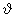 a kibocsátott fényhullám terjedési irányának az elektron (eredeti) mozgásirányával
bezárt szöge. Írható tehát:
a kibocsátott fényhullám terjedési irányának az elektron (eredeti) mozgásirányával
bezárt szöge. Írható tehát:
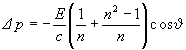
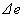 = - E egyenletet felhasználva,
innen a
= - E egyenletet felhasználva,
innen a
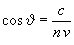
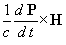
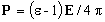 az egységnyi térfogatban foglalt dipólmomentum.]
A (10) alatti Minkowski-féle erősűrűség nyilván nem foglalhatja magában a (15) kifejezést, hiszen (10)-ben sem a mágneses
térerősség, sem pedig időszerinti derivált nem szerepel. A (9) Abraham-féle erőtörvényből ugyanekkor minden külön feltevés
nélkül megkaphatjuk a kívánt (15) tagot. A d H / d t = - c rot E
Maxwell-egyenletet és a
az egységnyi térfogatban foglalt dipólmomentum.]
A (10) alatti Minkowski-féle erősűrűség nyilván nem foglalhatja magában a (15) kifejezést, hiszen (10)-ben sem a mágneses
térerősség, sem pedig időszerinti derivált nem szerepel. A (9) Abraham-féle erőtörvényből ugyanekkor minden külön feltevés
nélkül megkaphatjuk a kívánt (15) tagot. A d H / d t = - c rot E
Maxwell-egyenletet és a