Fizikai Szemle honlap |
Tartalomjegyzék |
Forrás: Fizikai Szemle 1971/12. 355.o.
Györgyi Géza
KFKI
A júliusi számban kísérletet tettünk a Kepler-probléma tárgyalására kizárólag középiskolás matematikával.1 A Kepler-mozgással nyilvánvalóan több tekintetben rokon a Rutherford-szórás problémája, azaz az alfa-részecskék mozgása a mag taszító Coulomb-erőterében. Mindkét esetben kúpszelet a pálya s az erő a távolság négyzetével fordítva arányos. A Naprendszer - a Nap és a bolygók - megfigyelése, a Kepler-mozgás tanulmányozása, előkészítette Newton gravitációs erőtörvényének felfedezését. A Rutherford-szórás megfigyelése (a Coulomb-törvény ismeretében) pedig döntő lépés volt az atom és alkotórészeinek megismeréséhez vezető úton. Éppen 60 évvel ezelőtt az atommag felfedezéséhez vezetett el.2
Ebben a cikkben - a Kepler-mozgás említett tárgyalásának mintájára - az alfa-részecskék Rutherford-féle mozgását mutatjuk be. Eltérően a legtöbbször követett úttól, 3 tárgyalásunk nem a Newton-féle mozgásegyenletek integrálásán alapul. A Rutherford-féle szórási képlethez vezető, itt követett út így a differenciál-egyenletek és megoldási módszereik terén nem jártasak számára is járható. "Differenciálási rutint" sem feltételeztünk, sem pedig a közvetett, az inverz, az implicit függvény, s a hiperbolikus szinusz és koszinusz deriválási szabályainak ismeretét. A szerző ismét bevallja: kiváltképp iskolás beszélgetőtársak kérdéseinek megválaszolására kereste a módot; talán remélheti, hogy cikkét mások - így középiskolai szakkört vezető kartársak - is figyelemre érdemesítik.
E cikk szorosan követi a korábbi Kepler-cikket.1 Az 1. szakaszban az (1.1) "egységhiperbolán" való mozgást vizsgáljuk; bevezetjük a hiperbolikus szinusz és koszinusz függvényeket. A 2. szakaszban nyújtással ill. zsugorítással tetszőleges excentricitású hiperbolapályára térünk át; levezetjük továbbá - a II. Kepler-törvénnyel analóg követelményből - Kepler időegyenletének analogonját. A 3. szakaszban a hodográfot (sebességábrát) határozzuk meg. A 4. szakaszban belátjuk, hogy a hiperbolapályán végbemenő Rutherford-mozgás gyorsulása - megfelelően Coulomb erőtörvényének - a távolság négyzetével fordítva arányos. Az 5. szakaszban levezetjük a Rutherford-féle szórási képletet.
A 60 év előtti helyzetet, melyben Rutherford felfedezését tette, megigézően idézi fel C. G. Darwin a Bohr 70. születésnapjára kiadott ünnepi kötetben. 4 Tanulmányában hangsúlyozza: híres szórási törvényének levezetéséhez Rutherford a hiperbolákra vonatkozóan nem használt fel többet, mint amit az iskolásgyermekek is tudnak. Elmondja, hogy Rutherford már a mag felfedezésének idején gondolt arra, hogy az ilyen szórásfolyamatok ismereteket szolgáltathatnak magának a magnak az alakjára és szerkezetére vonatkozólag.
A magok Coulomb-gerjesztéses - a kiterjedt kísérleti adatgyűjtő munka s az adatokat szép egységes képbe foglaló "egyesített modell" - Rutherford e várakozását messzemenően igazolta. A Coulomb-gerjesztés meglepően pontos eredményeket adó félklasszikus tárgyalása 5 (melynek alapját a részecskepályák klasszikus tárgyalása képezi) mutatja: a Rutherford-mozgás problémája nem csak a magfizika hőskorának történetében, hanem aktuális fejezeteiben is fontos helyet foglal el.
Szintén fontos ismeretek forrása az elektronok szóródása magokon és nukleonokon. Napjaink fontos fejleménye, az ultranagy-energiájú elektronok "mély" inelasztikus szóródása, Rutherford 60 év előtti felfedezését idézi fel. A Stanfordi Lineáris Akcelerátor Központ kétmérföldes gyorsítója által 21 GeV-re gyorsított elektronokkal elvégzett vizsgálatokat ismertető tanulmányában 6 Kendall és Panofsky azt írja, hogy most, 60 év múltán, az atoménál 100 000-szer kisebb méretek közt talán megismétli magát a történelem. Az ultranagyenergiájú elektronok nukleonokon észlelt szóródása minden előzetes elképzelésnek ellentmond. A megfigyelések alapján feltehető, hogy a nukleonok összetett rendszert képeznek; feltételezett pont szerű alkotóelemeiknek a "parton" nevet adták. (A szóráskísérletek elemzésének alapját a Rutherford-formula általánosításai: Mott és Rosenbluth képletei képezik).
Még meg kell említeni, hogy rögzített ponttöltés Coulomb-terén szóródó töltött részecske differenciális szórási hatáskeresztmetszetére mind a klasszikus mechanika, mind a kvantummechanika alapján elvégzett számítás a Rutherford-formulát adja. Ezt a fizika fejlődésében különösen szerencsés körülményt Norcliffe, Percival és Roberts elemezte a kvantummechanika Feynman-féle megfogalmazásának keretei között. 7
1. Mozgás egyenlőszárú hiperbolán, a centrumra vonatkozó területi sebesség const. értéke mellett. Kiindulásképpen adott hiperbolapályához kötött részecske mozgásával foglalkozunk. A pálya legyen a fél valós tengely egységnyi értékével jellemzett
|
x2 - y2 = 1 |
(1.1) |
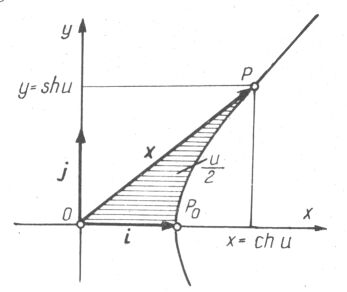
egyenlőszárú hiperbola jobb ága. A részecske (jele legyen P) helyzetét meghatározhatjuk x, y Descartes-koordinátái segítségével. De jellemezhetjük azon OP0P síkidom u kétszeres - előjeles területével is, melyen a hiperbola O centrumát a részecskével összekötő vektor végigseper, miközben a részecske P0-ból az x, y koordinátájú pontba mozog (lásd az 1. ábrát; az alsó félsíkon fekvő pontok esetében az u kétszeres terület negatív szám); u megadása x-et és y-t egyértelműen meghatározza:
|
x = ch u, y = sh u |
(1.2) |
Ez definiálja az sh és ch hiperbolikus szinusz és koszinusz függvényeket. Felhasználandó tulajdonságaikat alább e definíció alapján állapítjuk meg majd.
Az O-t P-vel összekötő x helyvektor a Descartes-rendszer tengelyei irányába mutató i, j egységvektorok segítségével az
|
x = i ch u + j sh u |
(1.3) |
alakban írható fel. A terület, melyen x egységnyi idő alatt végigseper, legyen const. ; a konstans értékét 1/2-nek választjuk. A
![]() kétszeres területi sebesség értéke tehát egy. Jelölje az u-hoz tartozó
kétszeres területi sebesség értéke tehát egy. Jelölje az u-hoz tartozó
x vektort részletesebben x(u), a megfelelő Descartes-koordinátákat pedig x(u) és y(u). Növeljük meg u-t ![]() -val; x(u) ekkor x(u +
-val; x(u) ekkor x(u +![]() ) = x(u) +
) = x(u) + ![]() -re, x(u) és y(u) pedig x(u +
-re, x(u) és y(u) pedig x(u + ![]() ) = x(u) +
) = x(u) +![]() -re, ill. y(u +
-re, ill. y(u + ![]() ) = y(u) +
) = y(u) + ![]() -ra változik. A
-ra változik. A ![]() /
/![]() vektor a
vektor a ![]() elmozdulásnak megfelelő átlagsebesség.
elmozdulásnak megfelelő átlagsebesség.
*
Az x + ![]() , y +
, y + ![]() megváltozott koordinátákra (1.1) ugyancsak teljesül:
megváltozott koordinátákra (1.1) ugyancsak teljesül:
|
|
(1.4) |
Osszuk el (1.4) és (1.1) különbségét 2![]() -val, majd tartson
-val, majd tartson ![]() zérushoz. Ily módon az
zérushoz. Ily módon az
|
|
(1.5) |
eredményt kapjuk.
Annak a síkidomnak az előjeles területe, amelyen a helyzetvektor, míg x-ről x + ![]() -re változik, végigseper,
-re változik, végigseper, ![]() / 2-vel egyenlő. Ugyanez a terület közelítőleg kifejezhető az x, y koordinátákkal és
/ 2-vel egyenlő. Ugyanez a terület közelítőleg kifejezhető az x, y koordinátákkal és ![]() ,
, ![]() megváltozásaikkal is (lásd a 2. ábrát.). Az x és x +
megváltozásaikkal is (lásd a 2. ábrát.). Az x és x + ![]() helyvektorú pontok s az O centrum mint szögpontok által meghatározott háromszög előjeles területe
helyvektorú pontok s az O centrum mint szögpontok által meghatározott háromszög előjeles területe
|
|
(1.6) |
[Az y = 0 speciális esetben e területképlet helyessége nyilvánvaló. Tetszőleges x, y esetére is nyomban belátjuk érvényességét, ha tekintetbe vesszük, hogy a Descartes-rendszer elforgatásakor az (1.6) kifejezés alakja változatlan marad.] Minél kisebb a ![]() növekmény, annál jobb közelítése (1.6) a
növekmény, annál jobb közelítése (1.6) a ![]() /2 területnek;
/2 területnek; ![]()
![]() esetén hányadosuk egyhez tart:
esetén hányadosuk egyhez tart:
|
|
(1.7) |
Az (1.5), (1.7) relációk jobb oldalán álló lineár is egyenletek megoldása, ha még tekintetbe vesszük
(1.1)-et is, dx/du = y és dy/du = x; (1.2) figyelembe vételével írhatjuk:
|
|
(1.8) |
|
|
(1.9) |
A ![]() átlagsebesség határértékét, a dx/du (tangenciális) sebességvektort, jelölje röviden t; (1.3), (1.8), (1.9) értelmében
átlagsebesség határértékét, a dx/du (tangenciális) sebességvektort, jelölje röviden t; (1.3), (1.8), (1.9) értelmében
|
|
(1.10) |
2. A Rutherford-mozgás származtatása. Az 1. szakaszban szemügyre vett speciális mozgásból adott ![]() arányú, y irányú nyújtással vagy zsugorítással tetszőleges excentricitású hiperbolapályán végzett mozgást származtathatunk. Legyen
arányú, y irányú nyújtással vagy zsugorítással tetszőleges excentricitású hiperbolapályán végzett mozgást származtathatunk. Legyen ![]() ; P koordinátáinak (1.2) kifejezésében sh u-t szorozzuk meg a
; P koordinátáinak (1.2) kifejezésében sh u-t szorozzuk meg a ![]() tényezővel. E zsugorítás
tényezővel. E zsugorítás ![]() , ill. nyújtás
, ill. nyújtás ![]() P-nek az
P-nek az
|
|
(2.1) |
koordinátákkal jellemzett Q pontot felelteti meg
(3. ábra). A fél valós tengely egységnyi és az excentricitás ![]() értékével jellemzett hiperbolát kapunk. Valóban, egyszerűen meggyőződhetünk arról, hogy a Q pontnak a -
értékével jellemzett hiperbolát kapunk. Valóban, egyszerűen meggyőződhetünk arról, hogy a Q pontnak a -![]() , 0, ill.
, 0, ill. ![]() , 0 Descartes-koordinátájú gyújtópontoktól mért távolság-különbsége const. (= 2).
, 0 Descartes-koordinátájú gyújtópontoktól mért távolság-különbsége const. (= 2).
Tudjuk: u az OP0P síkidomnak - melyet a 3. ábrán vízszintes vonalkázás különböztet meg - a kétszeres területe. A függőlegesen bevonalkázott OP0Q idomot ebből az y irányú méretek ![]() arányú zsugorításával - ill. nyújtásával nyertük. A terület eközben ugyancsak
arányú zsugorításával - ill. nyújtásával nyertük. A terület eközben ugyancsak ![]() arányban változott. A terület, melyen az O-t P-vel összekötő helyzetvektor időegység alatt végigsepert (azaz a területi sebesség), 1/2 volt; Q területi sebességét ebből az
arányban változott. A terület, melyen az O-t P-vel összekötő helyzetvektor időegység alatt végigsepert (azaz a területi sebesség), 1/2 volt; Q területi sebességét ebből az ![]() tényezővel szorozva kapjuk. (Mind a két esetben az O centrumra vonatkoztatott területi sebességről van szó. )
tényezővel szorozva kapjuk. (Mind a két esetben az O centrumra vonatkoztatott területi sebességről van szó. )
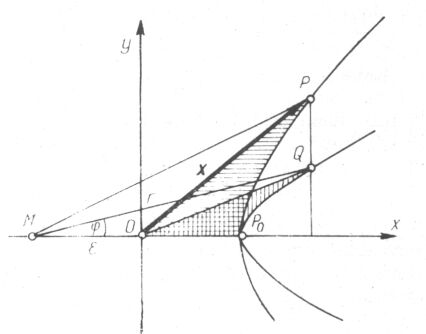
Módosítsuk most feltevésünket. A Q pontnak az O centrumra vonatkoztatott területi sebessége helyett Q-nak az M baloldali fókuszra vonatkoztatott területi sebességétől kívánjuk meg, hogy konstans legyen. Először az egyenlőszárú hiperbolán haladó P pontot vesszük szemügyre. A 3. ábrán az O-t a P-vel összekötő x vektor mellett az M-től P-hez vont egyenes szakaszt is láthatjuk. Neve legyen röviden MP vezérsugár.
Tudjuk: az OP0P (vízszintesen vonalkázott) síkidom területe u/2. Az MP vezérsugár által súrolt területet úgy kapjuk, hogy u/2-höz hozzáadjuk az MOP háromszög 1/2![]() shu területét. Feltesszük, hogy az MP vezérsugár által súrolt terület arányos az idővel. Eszerint 1/2 (u +
shu területét. Feltesszük, hogy az MP vezérsugár által súrolt terület arányos az idővel. Eszerint 1/2 (u + ![]() sh u) a t időnek állandószorosa; az állandót
sh u) a t időnek állandószorosa; az állandót ![]() -vel jelölve írható:
-vel jelölve írható:
|
|
(2.2) |
Ez annak feltétele, hogy az MP vezérsugár által súrolt terület arányos legyen az idővel. Az M-től Q-hoz vont vezérsugár által súrolt idom ebből ![]() arányú, y irányú nyújtással ill. zsugorítással állt elő, területe tehát az előbbinek
arányú, y irányú nyújtással ill. zsugorítással állt elő, területe tehát az előbbinek ![]() (= const.)-szorosa. Az M-től Q-hoz vont vezérsugár eszerint egyenlő idők alatt szintén egyenlő területeket súrol, azaz: Q-nak M-re vonatkoztatott területi sebessége konstans.
(= const.)-szorosa. Az M-től Q-hoz vont vezérsugár eszerint egyenlő idők alatt szintén egyenlő területeket súrol, azaz: Q-nak M-re vonatkoztatott területi sebessége konstans.
Más szóval: Q a (2.1) hiperbolapályán a II. Kepler-törvénnyel összhangban halad. A (2.2) összefüggés a Kepler-féle időegyenlet analogonja.
3. A Rutherford-mozgás hodográfja. A 2. szakaszban meghatároztuk u és t kapcsolatát azon feltevés alapján, hogy Q-nak az M fókuszra vonatkoztatott területe állandó legyen. Ebben a szakaszban a célunk: a sebesség, ill. a sebességnek a mozgás folyamán való változásait szemléltető hodográf (sebesség-ábra) meghatározása.
Az u-nak megfelelő t időt részletesebben jelöljük t(u)-val. Ha u-t ![]() -val megnöveljük, (2.2) baloldala
-val megnöveljük, (2.2) baloldala ![]() -val, a jobboldal
-val, a jobboldal ![]() -vel nő
-vel nő ![]() ;
; ![]() -vel osztva mind a két oldalt, kapjuk:
-vel osztva mind a két oldalt, kapjuk:
|
|
(3.1) |
Végezzük el a ![]() határátmenetet; (1.9) figyelembe vételével kapjuk:
határátmenetet; (1.9) figyelembe vételével kapjuk:
|
|
(3.2) |
Ennek birtokában könnyen meghatározható az (1.3) vektor
|
|
(3.3) |
differenciahányadosának határértéke, a ![]() deriváltvektor. Az első tényező (3.3) jobb oldalán (1.10)-hez, a második (3.2)-höz tart. Írható tehát:
deriváltvektor. Az első tényező (3.3) jobb oldalán (1.10)-hez, a második (3.2)-höz tart. Írható tehát:
|
|
(3.4) |
a wx, wy derékszögű sebességkomponensek:
|
|
(3.5) |
A (3.4), (3.5) képletek az (1.2) egyenlőszárú hiperbolán végzett mozgás sebességét adják meg. Az ![]() arányú, y irányú nyújtással, ill. zsugorítással nyert (2.1) hiperbolapályán haladó Q pont v sebességét ebből úgy kapjuk, ha (3.5) alatt wy-t
arányú, y irányú nyújtással, ill. zsugorítással nyert (2.1) hiperbolapályán haladó Q pont v sebességét ebből úgy kapjuk, ha (3.5) alatt wy-t ![]() -del szorozzuk meg; v derékszögű komponensei eszerint
-del szorozzuk meg; v derékszögű komponensei eszerint
|
|
(3.6) |
*
A (3.6) sebességkomponensek teljesítik a
|
|
(3.7) |
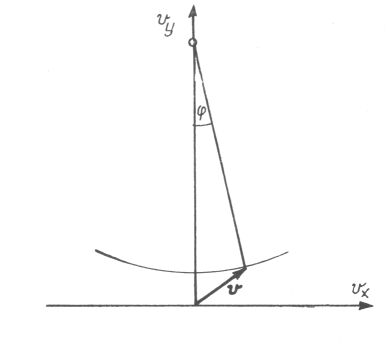
egyenletet. Ez ![]() sugarú kör egyenlete, melynek középpontja az ordinátatengelyen,
sugarú kör egyenlete, melynek középpontja az ordinátatengelyen, ![]() magasságban van. Megjegyzendő, hogy míg u végigfutja a valós számegyenest, v nem járja körül a kört egészen, csak a
magasságban van. Megjegyzendő, hogy míg u végigfutja a valós számegyenest, v nem járja körül a kört egészen, csak a ![]() (nyitott) ívet írja le. Ez a mozgás hodográfja
(4. ábra).
(nyitott) ívet írja le. Ez a mozgás hodográfja
(4. ábra).
Vezessük be a ![]() szöget a
szöget a
|
|
(3.8) |
összefüggések segítségével; ![]() az M-et Q-val összekötő vezérsugár
(3.ábra). A vezérsugár u-val, ill.
az M-et Q-val összekötő vezérsugár
(3.ábra). A vezérsugár u-val, ill. ![]() -vel (2.1) és (3.8) alapján az
-vel (2.1) és (3.8) alapján az
|
|
(3.9) |
alakban fejezhető ki. Az u, ![]() mennyiségek kapcsolatát kifejező összefüggések:
mennyiségek kapcsolatát kifejező összefüggések:
|
|
(3.10) |
|
|
(3.11) |
A (3.10) egyenletek alapján a (3.6) sebességkomponensek a
|
|
(3.12) |
alakban írhatók fel. A hodográf új paraméteres előállítását kaptuk; ![]() -t a 4. ábra szemlélteti.
-t a 4. ábra szemlélteti.
4. Rutherford-mozgás és Coulomb-taszítás. Határozzuk meg v végpontjának sebességét, vagyis a gyorsulást. Legyen ![]() s a
s a ![]() szög
szög ![]() idő alatt növekedjék
idő alatt növekedjék ![]() -vel;
-vel; ![]() komponensei (3.12) alapján:
komponensei (3.12) alapján:
|
|
(4.1) |
A ![]() /
/![]() differenciahányadost írjuk fel a
differenciahányadost írjuk fel a
|
|
(4.2) |
alakban. A (3.10) vagy a (3.11) képletek közül az első értelmében ![]() és u között fennáll a
és u között fennáll a
|
|
(4.3) |
összefüggés. Az ![]() megnövekedett értékekre szintén teljesül (4.3):
megnövekedett értékekre szintén teljesül (4.3):
|
|
(4.4) |
Vonjuk le (4.3)-at (4.4)-ből; ![]() -val osztva, csekély átalakítással kapjuk:
-val osztva, csekély átalakítással kapjuk:
|
|
(4.5) |
Végezzük el a ![]() határátmenetet. A színusz és koszinusz függvények differenciahányadosai (4.1) és (4.5) alatt a megfelelő
határátmenetet. A színusz és koszinusz függvények differenciahányadosai (4.1) és (4.5) alatt a megfelelő
|
|
(4.6) |
deriváltakhoz tartanak; ch u differenciahányadosának határértékét (1.8) adja meg. A (4.2) egyenlet jobb oldalán az első tényező határértéke ![]() ; (4.5)-ből kapjuk, (3.9) és (3.10) vagy (3.11) figyelembe vételével:
; (4.5)-ből kapjuk, (3.9) és (3.10) vagy (3.11) figyelembe vételével:
|
|
(4.7) |
A második tényező (4.2) jobb oldalán a (3.2) deriválthoz tart, amit (3.9) tekintetbe vételével így is írhatunk:
|
|
(4.8) |
A (4.2), (4.6), (4.7), (4.8) képletek alapján (4.1) határértékére kapjuk:
|
|
(4.9) |
Ugyanez vektoregyenletté összefoglalva:
|
(4.10) |
ahol r° az M gyújtóponttól a hiperbolapályán haladó Q pont (részecske) felé mutató egységvektor. A dv/dt gyorsulás, megfelelően Coulomb erőtörvényének, fordítva arányos a távolság négyzetével.
A fentiekben a hiperbolapálya fél valós tengelyét egynek választottuk; (4.10) erre az estre érvényes. Ha a fél valós tengely a, (4.10) alatt r helyére r/a, v helyére v/a helyettesítendő. Ekkor tehát
|
|
(4.11) |
Coulomb erőtörvényében r°/r2 együtthatója: a mag Ze töltése, szorozva a részecske ze töltésével, és osztva a részecske m tömegével; ![]() -t ezzel egyenlővé téve az
-t ezzel egyenlővé téve az
|
|
(4.12) |
összefüggést kapjuk. Ez bizonyos mértékig analóg a III. Kepler-törvénnyel. Természetesen a ![]() idődimenziójú konstans most nem a keringési idő. Mindamellett jellemzi a mozgást:
idődimenziójú konstans most nem a keringési idő. Mindamellett jellemzi a mozgást: ![]() mellett a részecske sebessége, osztva a fél valós tengellyel, a
mellett a részecske sebessége, osztva a fél valós tengellyel, a
|
|
(4.13) |
határértékhez tart.
5. A Rutherford-féle szórási képlet. Mint a 4. szakasz utolsó bekezdésében, a következőkben is legyen a fél valós tengely nagysága tetszőleges a érték. Ekkor (2.1) helyett
|
|
(5.1) |
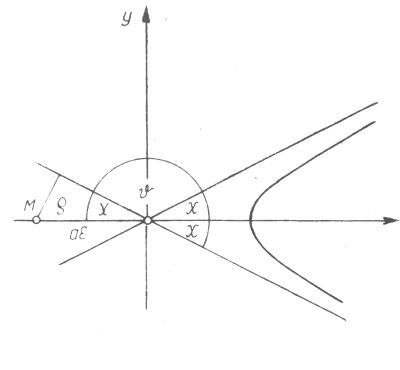
5. ábra
(3.12) helyett
|
|
(5.2) |
írandó. A (2.2), (5.1) egyenletek szerint a részecske, míg t < 0, az alsó félsíkon közeledik az erőcentrum felé, t > 0 esetén pedig a felső félsíkon távolodik tőle. Ha ![]() , (2.2), (3.11) és (5.2) értelmében a sebességkomponensek határértéke:
, (2.2), (3.11) és (5.2) értelmében a sebességkomponensek határértéke:
|
|
(5.3) |
v-nek az x-tengellyel bezárt szöge tehát a kezdeti ![]() értékről a végső
értékről a végső ![]() értékre változik, ahol
értékre változik, ahol ![]() . A szórás szöge eszerint
. A szórás szöge eszerint ![]() és így
és így
|
|
(5.4) |
Ha a közeledő részecskére nem hatna a taszító erő, mindvégig ![]() sebességgel haladna az
sebességgel haladna az ![]() aszimptota mentén s az erőcentrum mellett
aszimptota mentén s az erőcentrum mellett ![]() távolságra haladna el (5.
ábra). A
távolságra haladna el (5.
ábra). A ![]() ütközési paraméter a szórási szög segítségével (5.4) szerint a következő alakban írható fel:
ütközési paraméter a szórási szög segítségével (5.4) szerint a következő alakban írható fel:
|
|
(5.5) |
Megjegyzendő, hogy a fél valós tengely (4.12) és (4.13) szerint kifejezhető a szóró mag Ze töltésével, a szórt részecske ze töltésével, m tömegével és
![]() kezdeti sebességével:
kezdeti sebességével:
|
|
(5.6) |
Közeledjék az erőcentrum (mag) felé a kezdeti sebesség adott ![]() nagyságával és rögzített irányával jellemzett részecskenyaláb. Azok a részecskék, amelyek a mag köré, a kezdeti mozgásirányra merőleges síkban,
nagyságával és rögzített irányával jellemzett részecskenyaláb. Azok a részecskék, amelyek a mag köré, a kezdeti mozgásirányra merőleges síkban, ![]() belső és
belső és ![]() külső sugárral képzeletben megszerkesztett körgyűrűt "eltalálják", az (5.5)-tel adott
külső sugárral képzeletben megszerkesztett körgyűrűt "eltalálják", az (5.5)-tel adott ![]() s a
s a
|
|
(5.7) |
által adott ![]() közé eső szöggel szóródnak. Ezen körgyűrű területe (5.5), (5.7) alapján:
közé eső szöggel szóródnak. Ezen körgyűrű területe (5.5), (5.7) alapján:
|
|
(5.8) |
Ha az erőcentrumot képzeletben egységnyi sugarú gömbfelülettel vesszük körül, azon a ![]() és
és ![]() szórási szögek egy-egy "szélességi kört" jellemeznek; e körök által közrefogott gömböv magassága
szórási szögek egy-egy "szélességi kört" jellemeznek; e körök által közrefogott gömböv magassága ![]() , a felszíne pedig
, a felszíne pedig ![]() . Osszuk el ezzel, a "felszínnel" az (5.8) területet;
. Osszuk el ezzel, a "felszínnel" az (5.8) területet; ![]() mellett a
mellett a ![]() differenciális szórási hatáskeresztmetszet Rutherford-féle képletét kapjuk:
differenciális szórási hatáskeresztmetszet Rutherford-féle képletét kapjuk:
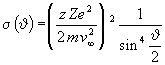
[felhasználtuk a-nak (5.6) alatt adott értékét is].
A mag felé haladó parallel nyalábban egységnyi keresztmetszeten egységnyi idő alatt haladjon át S (= const.) számú részecske. Ekkor az időegység alatt ![]() és közé eső szögű szórást szenvedő részecskék száma
és közé eső szögű szórást szenvedő részecskék száma ![]() .
.
________________________________
1
Györgyi G., A Kepler-mozgás és a gravitációs törvény. Fizikai Szemle, 1971. július. 205. old.2 E. Rutherford, Az alfa- és béta-részecskék szóródása anyagban, és az atom szerkezete. Magyar Fizikai Folyóirat, 4 (1956) 283.
3 L. D. Landau és E. M. Lifschitz, Mechanik. Akademie - Verlag, Berlin, 1963. 60. old. Györgyi G., Elméleti magfizika. Műszaki Könyvkiadó, Budapest, 1965. 36. old.
4 W. Pauli (Editor), Niels Bohr and the development of physics. Pergamon Press, London, 1955. 1. old.
5 L. C. Biedenharn és P. J. Brussaard, Coulomb excitation. Clarendon Press, Oxford, 1965.
6 H. W. Kendall és W. K. H. Panofsky, The structure of the proton and the neutron. Scientific American, 1971. június. 61. old.
7 A. Norcliffe és I. C. Percival, Correspondence identities I., II. J. Phys. B 1 (1968) 774, 784. A. Norcliffe, I. C. Percival és M. J. Roberts, Correspondence indentities III., IV. J. Phys. B 2 (1968) 578, 590.