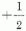 , illetve
, illetve 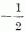 , ezért
, ezért
Fizikai Szemle honlap |
Tartalomjegyzék |
Zimányi József
KFKI
1961-ben a fizikusok megdöbbenve vették tudomásul, hogy közepes és nehéz magokban izobár analóg állapotokat fedeztek fel [1]. Az általános közhiedelem szerint. ugyanis ezek az állapotok nem létezhettek. E tévhit alapja a következő gondolatmenet volt: az izospin kvantumszám jósága valószínűleg attól függ, hogy a Coulomb energia elhanyagolható-e a nukleáris energia mellett; ez a feltétel teljesül a könnyű magokra, azért ott az egyes állapotokhoz egyértelműen hozzá tudjuk rendelni az izospin kvantumszámot., de a nehéz magoknál, ahol a Coulomb energia összemérhető a nukleárissal. az izospin kvantumszám használhatatlanná válik. A helyzet fonákságához tartozik, hogy bizonyos értelemben éppen a Coulomb erők miatt válik jó kvantumszámmá az izospin a nehéz magoknál. E látszólagos ellentmondás tisztázásához röviden idézzük fel az izospinre vonatkozó ismereteinket.
Az izospin [2] formailag teljes analógiát mutat. a közönséges spin kvantumszámmal. Ezért először azt vizsgáljuk meg, hogyan határozhatjuk meg egy mag-állapot S spinjét egy elvi kísérlettel. Tudjuk, hogy egy S spinű állapotnak a kvantálási tengelyre vonatkoztatott MS spin vetülete 2S + 1 különböző értéket vehet fel. Forgassuk el tehát atommagunkat először úgy, hogy spinvetülete a maxiális értéket (MS = S) vegye fel. Ezután számláljuk le, hogy hány lépésben lehet a magot az ellenkező irányba (a minimális, MS = - S spinvetületű állapotba) átforgatni, ha MS értéke lépésenként csak egy egységgel változhat. Az így kapott lépésszámot kettővel osztva kapjuk a magállapot spinjét.
Az atommag egy állapotának az izospinjét az előbbiekben leírtakhoz hasonlóan fogjuk megállapítani. Tegyük
fel, hogy az állapotot az 1a. ábra szerinti egyrészecske konfigurációval jellemezhetjük. Egy
N neutronból és Z protonból álló rendszer MT izospinvetület kvantumszámát úgy
kapjuk meg, hogy az egyes nukleonok izospinvetületeit összeadjuk. Mivel a neutron, illetve a proton
izospinvetülete 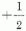 , illetve
, illetve 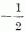 , ezért
, ezért
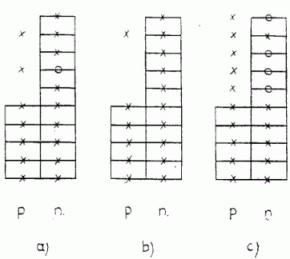
1. ábra. Az atommag egyrészecske konfigurációjának szemléletetése. A baloldali oszlopban a
proton-, a jobboldali oszlopban a neutron egyrészecske állapotokat tüntettük fel. A * és a ° a betöltött
és az üres állapotokat jelöli
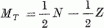 Az MT
izospin vetület értéke az 1a. ábránál
MTa = (Na - Za)/2 = 1,
ahol Na és Za a neutronok és a protonok száma. Eljárásunk szerint először
elforgatjuk a magot (az izospin térben) abba az állapotba, ahol MT a maximális értéket veszi fel.
Ehhez a p oszlopban, a proton állapotban levő nukleonokat a neutronállapotot jelző n
oszlopba kell áttolnunk. Ezt az áttolást azonban csak a Pauli-elvet figyelembe véve szabad megtennünk,
tehát a már betöltött neutron-állapotba nem rakhatunk be még egy nukleont. Így a maximális MT-vel
rendelkező 1b. ábrabeli állapotot kaptuk (MTb = 2). Most kezdjük el lépésenként
csökkenteni MT értékét, azaz a neutronokat egyenként áttoljuk protonállapotba (természetesen csak
olyanokba, amelyek még üresek). Így az 1b. ábrán feltüntetett állapotból négy lépésben jutunk el a
minimális MT-vel rendelkező 1c. ábrabeli
állapotba (MTc = - 2), tehát az állapot
izospin kvantumszáma T = 4/2 = 2. (Mivel a jelen tárgyalásmód szempontjából nem lényeges, csak
zárójelben említjük meg, hogy az 1. ábrabeli állapotok általában nem sajátfüggvényei a teljes
impulzusmomentumnak; ilyen állapotok lineárkombinációiból azonban az impulzusmomentum összeadás
szabályai szerint a teljes impulzusmomentum sajátállapota is előállítható.)
Az MT
izospin vetület értéke az 1a. ábránál
MTa = (Na - Za)/2 = 1,
ahol Na és Za a neutronok és a protonok száma. Eljárásunk szerint először
elforgatjuk a magot (az izospin térben) abba az állapotba, ahol MT a maximális értéket veszi fel.
Ehhez a p oszlopban, a proton állapotban levő nukleonokat a neutronállapotot jelző n
oszlopba kell áttolnunk. Ezt az áttolást azonban csak a Pauli-elvet figyelembe véve szabad megtennünk,
tehát a már betöltött neutron-állapotba nem rakhatunk be még egy nukleont. Így a maximális MT-vel
rendelkező 1b. ábrabeli állapotot kaptuk (MTb = 2). Most kezdjük el lépésenként
csökkenteni MT értékét, azaz a neutronokat egyenként áttoljuk protonállapotba (természetesen csak
olyanokba, amelyek még üresek). Így az 1b. ábrán feltüntetett állapotból négy lépésben jutunk el a
minimális MT-vel rendelkező 1c. ábrabeli
állapotba (MTc = - 2), tehát az állapot
izospin kvantumszáma T = 4/2 = 2. (Mivel a jelen tárgyalásmód szempontjából nem lényeges, csak
zárójelben említjük meg, hogy az 1. ábrabeli állapotok általában nem sajátfüggvényei a teljes
impulzusmomentumnak; ilyen állapotok lineárkombinációiból azonban az impulzusmomentum összeadás
szabályai szerint a teljes impulzusmomentum sajátállapota is előállítható.)
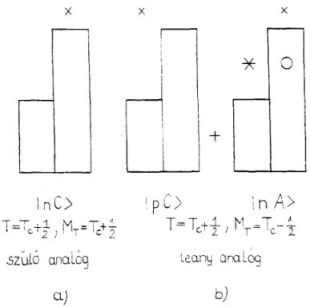
Az azonos T izospinű, de különböző MT-kvantum számú állapotok alkotják az izospin multiplettet [2]. A multiplett minden tagjában ugyanannyi nukleon van, tehát ezek izobárok. Továbbá, mivel a multiplett minden tagjában ugyanazok az egyrészecske állapotok vannak betöltve (hol protonnal, hol neutronnal), ezért ezek az állapotok hasonlítanak egymásra, mintegy egymás analógjai. Ennek alapján a multiplettben egymás mellett álló állapotokat izobár analóg állapotoknak, a második szomszédot második analóg állapotnak, stb. nevezzük. A nagyobb MT-jű állapotot szülőanalógnak, az eggyel kisebb MT-jű állapotot leányanalógnak is szokták nevezni.
Írjuk most le egy analóg állapot szerkezetét. A szülő-analóg állapot legyen a 2a. ábra szerinti. A fent elmondottak szerint ezen állapot maximális MT-jű, MT = T állapotban van. Egy egységgel kisebb MT-jű állapotot kapunk, ha a többlet neutronok bármelyikét proton állapotúra változtatjuk. Így ezen állapotok szuperpozíciójaként áll elő a 2a. ábrabeli szülő-analóg állapot leány-analóg állapota (2b. ábra).
2. ábra. Példa a szü1ő-analóg (a) és a hozzá tartozó leány-analóg (b) állapotra
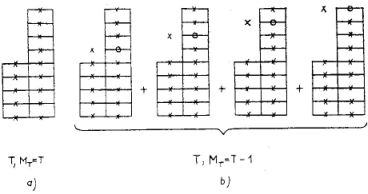
Az eddig elmondottak alapján most már megérthetjük [3], honnan származott az a téves hiedelem, hogy nehéz magok esetében az izospin rossz kvantumszám, és azt is, hogy miért volt hibás ez a nézet. Gondolatban kapcsoljuk ki a protonok elektromos terét. Állítsunk elő tiszta izospinű állapotot, pl. egy (T,MT = T)-vel jellemezhető állapotot (3a. ábra). Ha most bekapcsoljuk a Coulomb-erőt, az meg fogja zavarni ezt a képet, a 3a. ábra konfigurációjához sok luk-részecske gerjesztésű állapotot (3b. és 3c. ábra) fog hozzákeverni. Mivel az izospin a fent elmondottak alapján azzal hozható kapcsolatba, hogy mely egyrészecske állapotok vannak betöltve, érthető az a hiedelem, hogy a Coulomb-erő által létrehozott, sok luk-részecske gerjesztést tartalmazó keveréknek nem lesz meghatározott izospinje. Ha azonban jobban szemügyre vesszük a 3b. ábrát, látjuk, hogy az ilyen típusú állapotok izospinje megegyezik a 3a. ábra-belivel (ugyanannyi neutront tudunk balra tolni a 3b. ábrán, mint a 3a. ábrán). Eltérő izospinű állapotot csak akkor kapunk, ha a protont olyan magasan fekvő egyrészecske-állapotra (3c. ábra) gerjesztjük, amely egyrészecske állapot nincsen neutronnal betöltve (a 3c. ábrán legfelül levő protont először jobbra eltolhatjuk, s az így kapott ábráról leolvashatjuk, hogy kettővel több neutront tolhatunk rajta balra, mint a 3a. ábrán, tehát ezen állapot izospinje egy egységgel nagyobb, mint a 3a. ábrabeli állapoté). A legalsó neutronnal be nem töltött egyrészecske állapot energiája annál magasabban fekszik, minél több többletneutron van a magban. A Coulomb-erő hatására bekövetkező perturbáció következtében pedig egy adott állapot annál kevésbé keveredik a kiinduló állapothoz, minél jobban eltér energiája a perturbálatlan állapot energiájától. Így tehát arra a következtetésre jutottunk, hogy nehéz magoknál, ahol
3. ábra. A Coulomb erő perturbáló hatásának szemléltetése
a többlet neutronok száma nagy, a Coulomb-erő nem képes elrontani a mag-állapot izospin tisztaságát. A stabil nehéz magokban a nagy neutrontöbblet oka viszont éppen az elektrosztatikus erők jelenléte, így tehát éppen a nukleon-nukleon kölcsönhatás töltésszimmetriáját elrontó Coulomb erők következtében marad mégis elég jó kvantumszám az izospin.
Térjünk most vissza a bevezetőben említett nevezetes kísérlethez [1]. Bombázzunk egy A céltárgymagot protonokkal és mérjük az A(p, n)B reakcióban keletkező neutronok energiaspektrumát. Azt tapasztaljuk, hogy a neutronspektrum alacsony energiájú részén egy igen erős csúcs jelentkezik. Ez azt jelenti, hogy a (p, n) reakcióban keletkező B maradék magnak egy magasan gerjesztett állapota igen nagy valószínűséggel jön létre. Az ezen állapotra vezető reakció Q értéke (Q = (a reakcióban keletkező neutron kinetikus energiája) - (a bombázó proton kinetikus energiája) mindig megegyezik egy, a B magban levő proton Coulomb energiájával. Ezen összefüggés felismerése után már könnyű volt e reakciókat értelmezni. A bombázó proton-állapotú nukleon mintegy rugalmasan szóródik a céltárgymagon, de e szóródás közben töltésállapota megváltozik, neutron lesz belőle. A céltárgymag is majdnem változatlan marad, csak töltésállapota változik meg: az analóg állapotba alakul át. (Például ha a 2a. ábrabeli céltárgymagot bombázzuk protonnal, akkor az ilyen típusú reakció során a 2b. ábrabeli maradékmag és egy távozó neutron keletkezik.) Ezért e reakciókat kvázi elasztikus vagy töltéskicserélő reakcióknak nevezik.
Egy lényeges szempontot ki kell emelnünk e helyen. Az izobár analóg állapot a végmagnak egy igen magasan gerjesztett állapota (a gerjesztési energia tipikus értéke mintegy 10 MeV). Ilyen gerjesztési energiánál a mag nívósűrűsége igen nagy és a ténylegesen megvalósuló állapotok e tartományban meglehetősen komplikált szerkezetűek. Így azt várhatjuk, hogy egy egyszerű nukleon-konfiguráció igen sok tényleges állapotra oszlik szét, azaz az egyszerű állapot az energiaspektrumban nem egy keskeny csúcsban, hanem egy széles energia-tartományban valósul meg. Az izobár analóg állapot azonban, bár igen egyszerű szerkezetű, mégis keskeny csúcsként jelentkezik a spektrumban. Ezt a, tényt csak úgy értelmezhetjük, hogy a nagy sűrűségben jelen levő állapotok (háttér állapotok) izospinje megegyezik az alapállapot T0 = M0= (N-Z)/2 izospinjével és így a T = T0 + 1 izospinű analóg állapot nem tud szétoszlani a háttér állapotok között, mert az állapot keveredésekért felelős magerők csak azonos izospinű állapotok között hozhatnak létre keveredést (a magerők töltésfüggetlenek). Így tehát arra a következtetésre jutottunk, hogy az izospin még a nagy gerjesztési energiájú állapotokra is jó kvantumszám.
A töltéskicserélő reakciók matematikai leírására is igen egyszerű modell állítható fel [4]. Ismeretes, hogy a nukleon-nukleon kölcsönhatásban is szerepel egy tag, mely a két nukleon között töltéscserét is létre tud hozni:
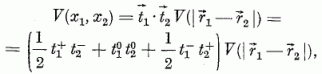
ahol  az izospin térben ható operátor;
t± = tx ±
itY, to = tz és tx, ty,
tz
az izospin operátor Descartes komponensei. Jelentését, hatását könnyen megérthetjük a közönséges spin
operátorokra való hivatkozással, hiszen formailag az izospin operátorok és függvények azonosak a közönséges
spin operátorokkal és függvényekkel. A
az izospin térben ható operátor;
t± = tx ±
itY, to = tz és tx, ty,
tz
az izospin operátor Descartes komponensei. Jelentését, hatását könnyen megérthetjük a közönséges spin
operátorokra való hivatkozással, hiszen formailag az izospin operátorok és függvények azonosak a közönséges
spin operátorokkal és függvényekkel. A 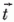 operátor hatását így foglalhatjuk össze:
operátor hatását így foglalhatjuk össze:
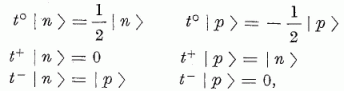
ahol | n > illetve | p > a nukleonnak neutron, illetve proton állapotát jelöli. (Ezen operátorok segítségével most már matematikailag is megfogalmazhatjuk, mit értünk azon, hogy egy nukleont pl. a proton állapotból neutron állapotba tolunk át (1. ábra). E célból egyszerűen egy t+ operátorral hatunk a szóbanforgó nukleon állapotfüggvényére. E művelet során a hullámfüggvénynek tér- és közönséges spin-koordinátáktól függő része változatlan marad.) A töltéskicserélő reakciók során a bombázó részecske a céltárgymag összes nukleonjával kölcsönhat. E kölcsönhatásnak a töltéskicserélő részét a fenti kétnukleon kölcsönhatások összege adja:
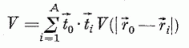
ahol a nullás index a bombázó részecskére, az i = 1-től A-ig terjedő indexek a céltárgymagban levő nukleonokra vonatkoznak. Mivel elsősorban a bombázó részecske sorsa érdekel minket, ezért a céltárgymagban levő nukleonok koordinátáira átlagolunk, így a térkoordináták közül csak a bombázó részecske koordinátája marad meg :
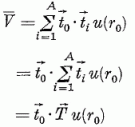
ahol 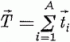 a céltárgymagra ható izospin operátor. Az ilyen módon közelítésként kapott kölcsönhatást
szimmetria-potenciálnak, vagy e modell [4] felállítójáról, Lane potenciálnak nevezzük. E potenciál
u(r0) alakfaktora lényegében a többlet neutronok sűrűségével egyezik meg [5]. Írjuk ki megint
a
a céltárgymagra ható izospin operátor. Az ilyen módon közelítésként kapott kölcsönhatást
szimmetria-potenciálnak, vagy e modell [4] felállítójáról, Lane potenciálnak nevezzük. E potenciál
u(r0) alakfaktora lényegében a többlet neutronok sűrűségével egyezik meg [5]. Írjuk ki megint
a 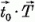 skalárszorzatot részletesen:
skalárszorzatot részletesen:
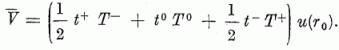
A T- operátor a céltárgymagban levő nukleonokra ható
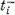 operátorok összege. Ha
tehát a T- operátort alkalmazzuk a céltárgymag | C> hullámfüggvényére, amit például a
2a. ábra szerinti konfigurációval jellemezhetünk, akkor eredményül éppen a 2b. ábra
szerinti konfigurációt, vagyis a | C> állapot izobár analógját, | A>-t kapjuk:
operátorok összege. Ha
tehát a T- operátort alkalmazzuk a céltárgymag | C> hullámfüggvényére, amit például a
2a. ábra szerinti konfigurációval jellemezhetünk, akkor eredményül éppen a 2b. ábra
szerinti konfigurációt, vagyis a | C> állapot izobár analógját, | A>-t kapjuk:
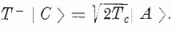
(A 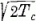 normálási tényező fellépte is jól
érthető a 2a. ábra alapján: a többlet neutronok száma
2Tc, tehát ennyi tagból áll az analóg állapot hullámfüggvénye, ha részletesen
kiírjuk; az itt kiírt | C > és | A> viszont egységre normált állapotfüggvények.)
normálási tényező fellépte is jól
érthető a 2a. ábra alapján: a többlet neutronok száma
2Tc, tehát ennyi tagból áll az analóg állapot hullámfüggvénye, ha részletesen
kiírjuk; az itt kiírt | C > és | A> viszont egységre normált állapotfüggvények.)
A nukleon és céltárgymag kölcsönhatásában fellépő Lane-potenciál teljesen számot tud adni a
töltéskicserélő reakciókról. A bombázó protont a 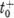 operátor neutron állapotba, és ezzel egyidejűleg a céltárgymagot a T- operátor az
izobár analóg állapotába viszi át. Az analóg állapot gerjesztéséhez szükséges energiát a bombázó részecske
energiájából kell fedezni, így a távozó neutron mozgási energiája az egy protonra jutó Δc
Coulomb energiával kevesebb. mint a bombázó proton kinetikus energiája.
operátor neutron állapotba, és ezzel egyidejűleg a céltárgymagot a T- operátor az
izobár analóg állapotába viszi át. Az analóg állapot gerjesztéséhez szükséges energiát a bombázó részecske
energiájából kell fedezni, így a távozó neutron mozgási energiája az egy protonra jutó Δc
Coulomb energiával kevesebb. mint a bombázó proton kinetikus energiája.
A szimmetria potenciál fellépte lényegesen megváltoztatja az egy nukleon mozgását leíró Schrödinger
egyenlet szerkezetét is. A 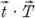 csatolótag
ugyanis összekapcsolja a céltárgymag terében mozgó proton | p > hullámfüggvényét
az analóg mag terében mozgó neutron | n > hullámfüggvényével [4].
A | p > és | n > függvénypárra kapott csatolt
differenciálegyenletet Lane egyenletnek nevezzük.
csatolótag
ugyanis összekapcsolja a céltárgymag terében mozgó proton | p > hullámfüggvényét
az analóg mag terében mozgó neutron | n > hullámfüggvényével [4].
A | p > és | n > függvénypárra kapott csatolt
differenciálegyenletet Lane egyenletnek nevezzük.
Vizsgáljuk meg mi történik, ha az A(p, n)B töltéskicserélő reakciót létrehozó. bombázó proton
mozgási energiáját csökkentjük. Láttuk, hogy a neutron számára a reakció során En = Ep - Δc
energia marad. Ha a bombázó proton Ep kinetikus energiáját a Δc Coulomb energia
alá csökkentjük, a neutron számára már csak negatív En energia marad, így az nem tud elmenni: a
kvázielasztikus szóródás nem jön létre, az analóg csatornának nem jut lényeges szerep a proton szóródásban.
Ha azonban az Ep bombázó energiát annyira csökkentjük, hogy a neutronra
jutó En
energia megegyezik egy-, a céltárgymag analógjának a terében létrejövő neutron egyrészecske állapot
kötési energiájával, a rendszernek egy rezonancia- állapota jön létre, amit a proton szórási
hatáskeresztmetszetben fellépő éles rezonancia is jelez. Ez az izobár analóg rezonancia (I. A. R.). Érdekes,
hogy a kvánzielasztikus szórás végállapotaként keletkező analóg állapotok 1961-ben történt észlelése
után három év telt el, amíg 1964-ben felfedezték az első közbülső állapotként létrejövő analóg állapotot,
az izobár analóg rezonanciát [6]. Ez a késés azért is meglepő, mert a
kvázielasztikus szórást leíró
Lane egyenletek ugyanolyan jól leírják ezt a folyamatot i, [7].
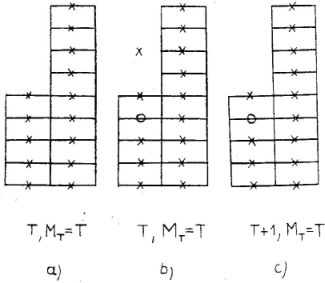
E rezonancia szerkezetét mutatja a
4. ábra. A 4a. ábra a Tc,
MT = Tc kvantumszámokkal jellemzett céltárgymag
plusz egy neutron rendszert mutatja. Ezen állapot izospin kvantumszámai
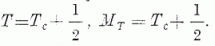 .
.
4. ábra. A neutron + céltárgymag rendszernek a leányanalóg állapota, mely izobár analóg
rezonanciaként
jelentkezik. A céltárgymagban levő egyrészecske állapotok részletezett jelölését most elhagytuk. Úgyszintén a
törzs analógjának a 2b. ábra szerinti szerkezetét is rövidítve tüntettük fel a
4b. ábrán
E rendszer analóg állapotát a 2. ábrával kapcsolatban mondottak szerint úgy
kapjuk, hogy a többlet neutronokból egyet-egyet proton állapotba tolunk át. Így kapjuk a
4b. ábrával szemléltetett állapotot, melynek izospin kvantumszámai
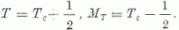 . Jelöljük a proton + céltárgymag
rendszer hullámfüggvényét | p C >-vel, a neutron + céltárgymag analógja rendszer
hullámfüggvényét | n A > -val. Az izospinek összeadására vonatkozó szabályok alapján
az izobár analóg rezonancia. (I. A. R.) hullámfüggvénye így írható:
. Jelöljük a proton + céltárgymag
rendszer hullámfüggvényét | p C >-vel, a neutron + céltárgymag analógja rendszer
hullámfüggvényét | n A > -val. Az izospinek összeadására vonatkozó szabályok alapján
az izobár analóg rezonancia. (I. A. R.) hullámfüggvénye így írható:
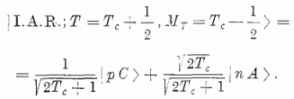
Mivel az izobár analóg rezonancia szerkezete igen hasonló a szülő-analóg szerkezetéhez, e rezonanciák vizsgálatával a szülő-analóg állapot összetételét is meg tudjuk határozni. Az I. A. R. struktúrájának részletesebb meghatározásához a protonok rugalmas és rugalmatlan szórásán kívül e rezonanciák gamma sugárzással való bomlását kellett megnézni [8], [9]. Az izobár analóg rezonanciák jellegzetes tulajdonságait a Lane-egyenletek alapján jól lehetett értelmezni [10], a részletes leíráshoz azonban a céltárgymagban levő nukleonokat is egyedileg kezelő mikroszkopikus modellekre volt szükség [11].
Térjünk most vissza a 4b. ábrához. Azt mutatja ez a vázlat, hogy milyen
rész-összetevőket kapunk,
ha egy (Tc, MT = Tc) izospinű maghoz
hozzácsatolunk egy 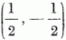 izospinű protont.
E két komponenst a fent felírt módon összeadva kaptuk a
izospinű protont.
E két komponenst a fent felírt módon összeadva kaptuk a 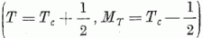 izospinű állapotot.
Tudjuk azonban, hogy ha egy L impulzusmomentumú maghoz egy
izospinű állapotot.
Tudjuk azonban, hogy ha egy L impulzusmomentumú maghoz egy 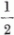 impulzusmomentumú nukleont adunk hozzá, akkor nemcsak a
impulzusmomentumú nukleont adunk hozzá, akkor nemcsak a 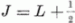 ,
hanem a
,
hanem a 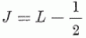 impulzusmomentumú állapot is létrejöhet. Hasonló módon, a céltárgymaghoz egy protont hozzáadva
nemcsak a
impulzusmomentumú állapot is létrejöhet. Hasonló módon, a céltárgymaghoz egy protont hozzáadva
nemcsak a 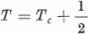 , hanem a
, hanem a
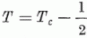 izospinű állapot is létrejöhet a következő
hullámfüggvénnyel
izospinű állapot is létrejöhet a következő
hullámfüggvénnyel
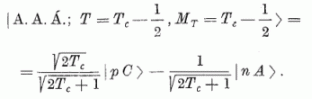
Ez az állapot az anti-analóg cállapot (A. A. Á. ) Energiája sok MeV-vel az I. A. R. alatt van. Ez az állapot általában nem található meg az atommagokban, mert izospinje (ami egy egységgel kisebb az I.A.R. izospinjénél) megegyezik a körülötte sűrűn elhelyezkedő háttérállapotokéval és így az izospin megmaradás nem védi meg a háttérállapotokra való szétszóródástól. Azonban olyan magokban, amelyekben az A.A.Á. paritása eltér a környező állapotok paritásától, a paritásmegmaradás tartja egy állapotra koncentrálva az anti-analóg állapotot. Ebben az esetben az LA.R. gamma bomlása nagy valószínűséggel az A.A.Á-ra vezet [12].
Az előzőekben azt vizsgáltuk, milyen következményekre vezet a bombázó részecske és a céltárgymag között ható Lane potenciál. Érdekes hatások lépnek fel azonban akkor is, ha ez a kölcsönhatás egy reakcióban keletkező részecskére hat. Az A(d,p)B reakcióban keletkező proton és a B végmag közti izospin függő kölcsönhatás miatt a proton mintegy a reakció második lépéseként töltéskicserélő szóródást szenved a B magon. Annál a bombázó deutron energiánál, amelynél e "kétlépéses folyamat" megindulhat, a (d, p) reakció igen markáns anomáliákat mutat [13].
A közepes és nehéz magokban fellépő izobár analóg állapotok tanulmányozása az elmúlt tíz évben kétségtelenül a magfizikának a legnagyobb intenzitással vizsgált területe volt. Ez idő alatt a speciálisan az analóg állapotokkal kapcsolatos problémák túlnyomó része tisztázódott. E kutatások igen sokban hozzájárultak ahhoz, hogy egy tökéletesebb kép alakuljon ki az atommagról.
E rövid összefoglalónkkal azt kívántuk megmutatni, hogy mi az a jelenségkör, amire e vizsgálatok irányultak és hogy hazai kutatóink hogyan kapcsolódtak be e felderítő munkába.