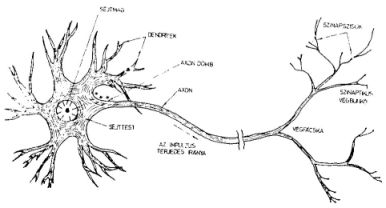
1. ábra A neuron alakja és egyes részeinek elnevezései
Fizikai Szemle honlap |
Tartalomjegyzék |
Zimányi József és Csernai László
MTA Központi Fizikai Kutató Intézet
1. Bevezetés
Az idegrendszer kutatása során az elmúlt évtizedek alatt rendkívül nagy ismeretanyag halmozódott fel. Az anatómiában, a neurofiziológiában, a biológiában és pszichológiában összegyűlt adatok tömege meghaladta azt a kritikus értéket, amelynek elérése után elkezdődhettek az ezen adatok egységbe foglalását célzó vizsgálatok.
A magasabbrendű élőlények a környezetükből az érzékelőikhez érkező hatásokat az idegrendszerükkel dolgozzák fel és e feldolgozás eredményétől (és természetesen belső állapotuktól) függően hajtanak végre különböző cselekvéseket. Az idegrendszer feladata tehát információk feldolgozása, döntéshozás, utasítás kiadása cselekvésre. A későbbiekre hagyjuk annak taglalását, hogy a pszichés gondolkodási folyamatokat és a tudatot hol és hogyan kíséreljük meg elhelyezni ezen képünkben.
Az idegrendszer működésének leírására az elmúlt 1-2 évtized alatt rendkívül sok modellt javasoltak. Sokrétűségük ellenére ezen modellek túlnyomó része közös tőről fakad és egy egységes elmélet kialakulásához vezető lépésnek tekinthető. Az idegrendszerről alkotott, egyre gyarapodó ismereteink alkotják a modellek alapját. Ma már elég jó képünk van az idegrendszert alkotó sejtek, a neuronok speciális működéséről, a neuronok egymáshoz való kapcsolódásának szabályosságairól és az így kialakult neuronhálózat szerkezetéről.
Jelen cikkben a figyelem felkeltésének céljával az idegrendszer matematikai modellezésébe kívánunk bepillantást nyújtani.

1. ábra A neuron alakja és egyes részeinek elnevezései
A neuron sematikus bemutatása után a neuronokat egyenként leíró mikroszkopikus elméletek alapját képező neuron egy modelljét mutatjuk be, majd pedig az ilyen neuronokból felépülő hálózat tulajdonságait vizsgáljuk. Ezután a nagyszámú neuronból álló, bizonyos szabályszerű szerkezetet mutató neuronhálózat tárgyalására bemutatjuk a neuronok átlagos állapotának fogalmát bevezető neuron tér modellt. E modell segítségével a neuronhálózatban lejátszódó kollektív jelenségek leírására mutatunk példákat.
Végezetül érintünk majd néhány problémát, amely a magasabbrendű gondolkodás, a tudat értelmezésével kapcsolatos.
2. A neuron sematikus bemutatása
A fejezet célja, hogy röviden leírja a neuronok általánosan jellemző tulajdonságait, ezek közül is főleg csak azokat, amelyek a neuronhálózatok matematikai modellezéséhez szükségesek.
A neuron egy sejt, amelynek van sejtmagja, sejtteste és membránja, mint a sejteknek általában, azonban két lényeges vonásban mégis különböznek az egyéb sejttípusoktól. Az egyik jellegzetesség a sejt alakja (1. ábra). A neuronokból sok nyúlvány ágazik ki. A nyúlványok többsége (néha többezer egy sejten) vékonyabb és rövidebb (legfeljebb 400 ,u) - ezeket dendriteknek nevezzük.
A nyúlványok másik fajtája az axon, vastagabb és hosszabb. Hosszuk a méteres nagyságrendet is elérheti. Általában sejtenként csak egy indul ki a 'sejttestről, ez azonban elágazik, ún. végfácskát alkot. A végfácska ágai kis bunkókban, ún. szinaptikus bunkókban végződnek és ezek más neuronsejtek dendritjével vagy sejttestével érintkeznek. Ez az érintkezés, a szinapszis, kémiai jellegű kapcsolatot létesít a neuronok között. Így a neuronok egymással összekapcsolódva bonyolult hálózatot alkotnak.
A másik jellegzetesség a neuron membránjának működésében rejlik. A neuron belső része viszonylag nagy, ≈ - 90 mV potenciáleltérést mutat egyensúlyi állapotban a környezettől a sejtfal aktív működésének hatására. Ezt a potenciálkülönbséget a sejt anyagcseréjéből származó energiával tartja fenn. Ha valahol a sejt membránt inger (pl. elektromos vagy kémiai hatás) éri, ez megváltoztatja a különféle ionokra a sejtfal permeabilitását és természetesen a potenciálkülönbség is megváltozik. A sejt aktív folyamatai ezután visszaállítják az egyensúlyi potenciálkülönbséget, de az elektromos hatás a membrán mentén tovaterjed. Ez az elektromos idegi impulzus. Az impulzus általában gyengül. Ha azonban a különféle külső behatások összegeződve pozitív irányban elegendően nagy feszültségkülönbséget okoznak, akkor egy gyengítetlenül tovaterjedő impulzus keletkezik. (2. ábra.) Az idegsejt alakja miatt igen fontos, hogy az axon kiindulási helyén, az ún. axondombon, mekkora a potenciál. Ugyanis, ha itt elér egy adott küszöbértéket, akkor az axonon szalad végig egy kifutó impulzus, amely igen éles, gyorsan terjed, (v = 0,1 - 150 m/sec) és + 20-30 mV csúcsértéket is elérhet. A végfácskák bunkóin ez az impulzus olyan kémiai változásokat idéz elő, amelyek az érintkező sejtet ingerelhetik, azaz olyan potenciálváltozást hoznak létre a membránon, amely tovaterjedő impulzust eredményez az axonon. A szinapszisokban lejátszódó kémiai folyamatok, a szinapszis fajtájától függően azonban olyan negatív potenciálváltozást is előidézhetnek az axonnal érintkező sejtben, ami a -90 mV egyensúlyi potenciált még negatívabbá teszi, hyperpolarizálja. Ilyenkor nem keletkezik kifutó impulzus, sőt, ez a hatás meggátolhatja más szinapszisok gerjesztő hatását. Ezért az utóbbi szinapszisokat gátló, míg az előbbieket gerjesztő szinapszisoknak nevezzük. Egy sejttípus mindig csak egy féle hatást gyakorol axonján keresztül a vele érintkezésben levő sejtekre. A szinapszisok impulzus átadó, vagy gátló képessége változhat kémiai és biológiai hatásokra.
Az idegrendszer bonyolult neuronhálózatain tehát elektromos impulzusok futnak keresztül. Ezek vizsgálata nem könnyű feladat, hiszen az emberi agyban kb. 1010-1011 neuron van, amelyek 1013-1015 szinapszison keresztül kapcsolódnak egymással. Ilyen bonyolult rendszerek vizsgálatához mindenképpen hasznos, ha a matematikát hívjuk segítségül.
3. A perceptron
A változó szinapszis erősségű neuron jó modelljének tekinthető a perceptron [1] lényegét alkotó egység, a beérkező jelek lineárisan súlyozott összegét képező és az összeget küszöbdetektorral kiértékelő berendezés.
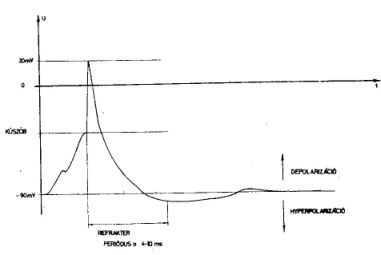
2. ábra Az elektromos impulzus időbeli lefutása az axon
egy pontján. Az impulzust követően a sejt rövid ideig újabb impulzus kibocsátására nem
ingerelhető. Ez az időszk a refrakter periódus
A perceptron működését a 3. ábrán szemléltetjük. A szemből és analizálóból álló berendezésnek különböző "α" ábrákat mutatnak. Célunk az, hogy a berendezés megtanuljon különbséget tenni az F+ és az F- halmazba tartozó ábrák között. Jó válasznak tekintjük az F+ halmazhoz tartozó ábra bemutatására adott "igen" és az F- halmazhoz tartozó ábra bemutatására adott "nem" válaszokat. Az ellenkező értékelést rossznak tekintjük. A külső felügyelő által végzett tanítás abban áll, hogy rossz válasz esetén a büntető gombot megnyomja, jó válasz esetén nem avatkozik be. A tanulás befejeződött, ha minden válasz jó.
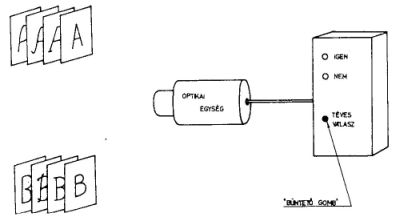
3. ábra A perceptron működése. Eredményes tanítás után
az optikai egység elé helyezett ábrákból a perceptron az F+ halmazhoz tartozókat
kiválasztja és az "igen" lámpa kigyulladásával jelzi. Téves jelzés esetén a büntető-gombot kell
megnyomni (azaz a tanítást folytatni kell.)
A perceptron szerkezetét a 4. ábrán mutatjuk be. A retina fényérzékelő elemekből áll. Innen vezetjük a jelek valamely kombinációját az asszociátor réteg "ai" elemeire. Az ai elemek a pi kimenetet produkálják:

A tömörebb jelölés kedvéért definiáljuk a pi(α)-ből álló p(α) oszlopvektort
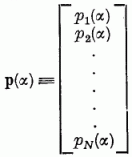
és a ci súlyokból álló c sorvektort
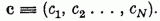
Az összegző egység a di pontokon belépő pi(α) jeleknek a ci súlyokkal súlyozott X(α) összegét állítja elő:
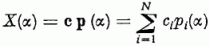
Ha a súlyozott összeg nagyobb, mint egy megadott küszöbérték, akkor a kimeneten jelet ("igen" választ) kapunk.
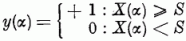
Az elmondottak alapján szembetűnő a hasonlóság az összegező rendszer és egy neuron között. A di belépési pontok a dendrit végződésnek a ci súlyok a szinapszis , erősségének felelnek meg. A pozitív ci a gerjesztő, a negatív ci a gátló szinapszis erősségeként fogható fel. A X(α) összeg a neuron gerjesztettségének felel meg. Ha ez a gerjesztettség meghaladja az S küszöbértéket, akkor az axonnak megfelelő kimeneten megjelenik az y kimenő jel. E hasonlóság ellenére egy jelentős különbségre is rá kell mutatnunk. A perceptronban a ci súlyok a tanulás során előjelet is válthatnak. Ennek a megfelelője a neuronoknál nem fordulhat elő. Egy szinapszis gerjesztő, illetve gátló karaktere nem változhat meg.
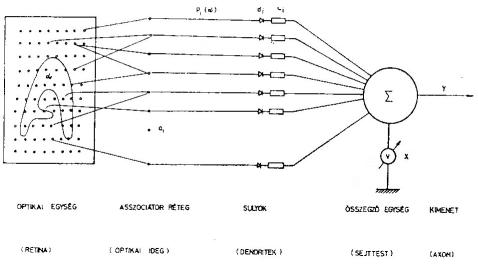
4. ábra. A perceptron szerkezetének vázlata. Zárójelben az egyes alkotórészek idegrendszerbeli
megfelelői
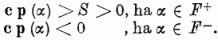
Kérdés, lehet-e olyan általános eljárást adni, amely a ci súlyokat úgy állítja be, hogy ezek az egyenlőtlenségek teljesüljenek. A perceptron konvergencia tétel szerint, ha létezik olyan c* vektor, melyre a fenti egyenlőtlenségek teljesülnek, akkor az alábbiakban leírt algoritmus véges számú lépésben meghatároz egy olyan c vektort, mely eleget tesz a fenti egyenlőtlenségnek. (Ez a c vektor nem szükségképpen azonos c*-gal.)
A tanító algoritmus:

A konvergencia tétel szerint ez az algoritmus csak véges számszor megy a c-t módosító részekre, ha egyáltalán létezik az egyenlőtlenségnek eleget tevő c* vektor. A következőkben ezt az állítást bizonyítjuk.
Definiáljuk a Ψ(α) vektort:
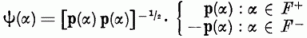
E Ψ-vektor segítségével a c p (α)-ra vonatkozó egyenlőtlenségek egyetlen egyenlőtlenségbe foglalhatók össze:

Tétel:
Ha létezik olyan c* vektor (| c* | = 1) és δ > 0 szám, hogy
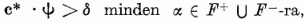
akkor véges számú lépésben meghatároz egy ilyen vektort a következő algoritmus:

Bizonyítás:
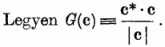
Mivel | c* | = 1, így G(c) két egységnyi abszolút értékű vektor skaláris szorzata, következésképp
G(c) < 1.
Az eljárásnak az AD címkéjű módosító részénél n-edik alkalommal módosított vektort jelöljük cn+1-gyel. (A kezdő vektort jelöljük c1-gyel, c1 = Ψ.) Az algoritmus szerint
cn+1 = cn + Ψ
A G(c) számlálója:
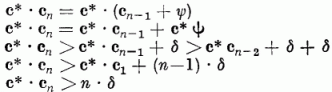
Tehát G(c) számlálója lineárisan növekszik az AD alatti változtatások számával. A nevező változását a következő módon becsülhetjük:
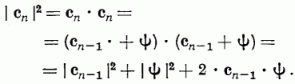
Igaz viszont, hogy
Cn-1 · Ψ ≤ 0
hiszen ez a feltétele annak, hogy az AD módosításhoz kerüljünk. Ezért, valamint figyelembevéve, hogy | Ψ | = 1:
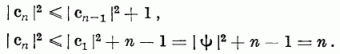
Tehát G(c) nevezőjének változása:
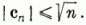
Így igaz, hogy
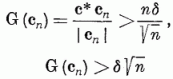
G (c) bevezetésekor megmutattuk, hogy G (c) < 1, ezért
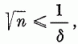
azaz a megadott eljárás csak véges számszor módosítja a c súlyvektort. Más szavakkal: az eljárás véges számú lépésben befejezi az alakfelismerés megtanítását. Ezzel a perceptron konvergencia tételt bebizonyítottuk.
A perceptronnal kapcsolatban, születése idején, igen nagy optimizmussal az a hiedelem is felmerült, hogy az a tanulni képes agy modelljének tekinthető. E hiedelem ugyan nem bizonyult igaznak, a perceptronra vonatkozó kutatások azonban világosan mutatják, hogy az idegrendszer atomjának tekinthető egyetlen neuron is milyen sokra képes.
4. A neurohálózat egyenletei
Az idegrendszer belső részein egy kiszemelt neuron (pl. az i-edik) más neuronoktól kaphat jeleket és saját maga is küld jelekét neuronoknak. Tekintsük példaként a kisagy kérget. Az itt található Purkinje sejt (5. ábra) feleltethető most meg a perceptron súlyozott összeget képező egységének. Az ábra, amit a Purkinje sejt észlel, a párhuzamos szálakon futó gerjesztésekből alakul ki. Az ábrát most is egy p(t) vektorral jelöljük. Ennek komponensei (p1(t), p2(t), ..., pN(t)) 1 vagy 0 értékűek aszerint, hogy az adott időintervallumban az 1, 2, ..., N-edik párhuzamos szálon van-e gerjesztés a kiszemelt Purkinje dendrit fájánál, az érzékelő bemeneténél. Az ábra szót itt általánosított értelemben használjuk: optikai szempontból jelentéssel nem bíró pontok halmaza, mely a párhuzamos szálakat képzeletben elmetsző síkban, a Purkinje-sejt "látósíkjában" jelenik meg. Az időt diszkréten változónak tekintjük. (A diszkrét időintervallum hosszát, τ-t, választhatjuk pl. 1 msec nagyságúnak; ez megfelel kb. egy impulzus időbeli hosszának.) Egy időkvantumon belül a sejtek állapotát változatlannak tekintjük. A változás az egyik időkvantumról a másikra való áttérés során következik be. Az i-edik Purkinje sejt testén mérhető gerjesztettségét a t + τ időben jelöljük Xi(t + τ)-val.
Az Xi változását a következő tényezők okozzák:
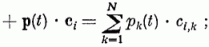
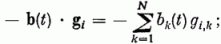
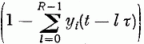 -val.
-val.
Mindezeket egybegyűjtve a gerjesztettséget a következő egyenlettel írhatjuk le:
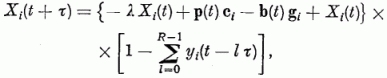
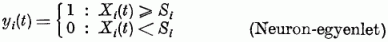
ahol λ a felejtés erőssége, ci,k az i-edik Purkinje sejtnek a k-adik párhuzamos szál felől való gerjeszthetősége (szinapszis erőssége), gi,k a k-ik gátló sejttel való kapcsolat erőssége, bk(t) á k-adik gátló sejtről érkező gátlás, pi(t) az i-edik párhuzamos rostról érkező gerjesztés. Si az érzékenységi küszöb, melyet, ha meghalad a gerjesztés, egy kifutó hullámot (szolitont) emittál a Purkinje sejt az axonján. (yi(t) = 1). R · τ a refrakter idő, ami alatt a sejt nem gerjeszthető. Az egymással kölcsönhatásban levő neuronok állapotát leíró fenti egyenletrendszer megoldására az adiabatikus közelítés alkalmazható. A λ, ci, gi mennyiségek sokkal lassabban változnak, mint az Xi gerjesztettségek, így az előbbieket konstansnak tekintjük a neuronhálózat egy aktivitási mintázatának a meghatározásakor.
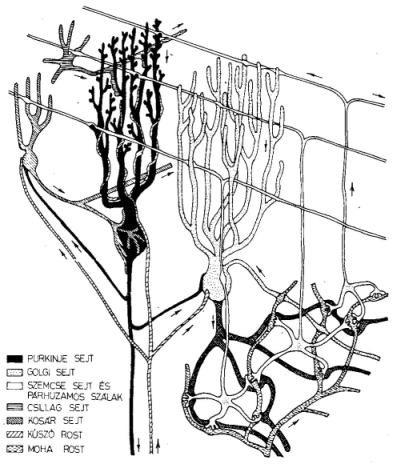
5. ábra. A kisagy-beli Purkinje-sejt sematikus képe. Felül az ágazatos dendritfán
keresztül kap a sejt ingereket az ún. parallel rostokon át. Ezeken a rostokon érkezik meg az izmok
állapotát és a testhelyzetet tükröző "kép" a feldolgozó sejtekre
A csatolási erősségekre sokkal nagyobb időállandókkal jellemezhető egyenleteket, a memória egyenleteket írjuk fel. Ebben azt a tanulási hypotézist fogalmazzuk meg, hogy
Ezen feltevés alapján a memória-egyenlet a következő:
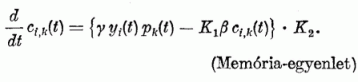
A K1 és K2 a szinapszis erősségét két korlát között tartja. Egyrészt a rég nem használt kapcsolatot sem hagyja teljesen eltűnni, másrészt a nagyon gyakran eredményesen működő kapcsolatot sem hagyja minden határon túl növekedni:
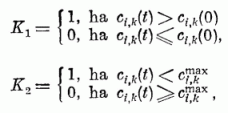
A gátló szinapszis erősségek nem változnak.
A fenti egyenleteket ugyan a kisagy-kéreg példája kapcsán írtuk fel, mégis vonatkoztathatjuk a teljes idegrendszerre. Ebben az esetben a p(t) vektor az összes neuron kimenete által az i-edik neuron szinapszisain a t időben létrehozott gerjesztést jelenti. Hasonlóan kiterjesztendő a b(t) gátló impulzuskép értelmezése is.
A konnektivitást, (azaz az idegrendszer kapcsolási rajzát) a ci,k szinapszis erősségek zérus, illetve nem zérus értékei reprezentálják (a hosszú axonokon való jel-terjedés véges sebességét ütem késleltetéssel könnyen figyelembe lehet venni). Receptor neuronok esetén p(t)ci a kívülről ható stimulus-ábrát jelenti.
A hálózat. állapotát mikroszkopikusan leíró egyenletrendszert felírtuk. Ez a leírás [4] korábbi egyszerűbb modellekből [3] alakult ki. Sokkal nagyobb nehézséget jelent azonban ezen egyenletek megoldásainak megkeresése és értelmezése. E probléma vizsgálatára alkalmazott néhány módszert mutatunk be a következőkben.
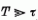 időintervallumban
a beérkező p(t) és b(t) inger ábrák stacionáriusak.
időintervallumban
a beérkező p(t) és b(t) inger ábrák stacionáriusak.
Ezen feltevések mellett a T idő alatt bekövetkező gerjesztettség változásra a neuron-egyenlet így írható:
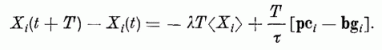
Osszuk el mindkét oldalt az Si küszöbértékkel és T-vel:
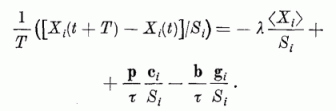
Ezen egyenlet baloldala azt adja meg, hogy T idő alatt az Si küszöbnek hányszorosára nőne a gerjesztés, amikor Xi nullára esne vissza. Ez tehát éppen a kimenő jelek frekvenciája, vi. A pk/τ és bl/τ értékek pedig a bejövő frekvenciák, vp,k és vb,l. Egy ai,k = ci,k/Si illetve di,l = gi,l/Si azt adja meg, hogy a k-ik, illetve az l-ik bemeneten megjelenő jel a küszöbérték hányad részével változtatja a gerjesztettséget. Ennek alapján a neuron egyenlet frekvenciák közti lineáris kapcsolatot előíró egyenletté alakul:
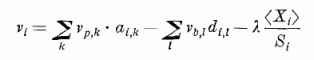
A neuronhálózat linearizált modelljében a "viselkedést" a bemenő frekvencia-mintázatra adott kimenő frekvencia-mintázat képviseli.
A memória kialakulásának leírására a Hebb, illetve Marr-féle [2] hipotézis itt is alkalmazható. A hálózat paramétereiként szereplő szinapszis erősségek változását, a sejtekre be-, és az onnan kifutó impulzusok frekvenciái határozzák meg:
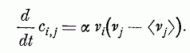
Kohonen [7] ilyen linearizált hálózatot vizsgált. Megmutatta, hogy ha egy hálózat egy adott ingerminta reprodukálását "megtanulta", akkor az inger egy részére is jó közelítéssel ugyanazt a választ adja, mint a teljes ingerre (6. ábra).
5. A neuronhálózat statisztikus leírása
A neuronok mikroszkopikus leírásának vannak hátrányai. Elsődlegesen az, hogy nagyszámú neuron egyedi matematikai leírása numerikusan nem lehetséges. A valóságban nincs is mindig szükség a neuronok működésének egyenkénti ismeretére. Az érzékelő rendszerben, a látás, tapintás területén nagyszámú, rétegekbe rendezett neuron dolgozza fel az információt. Ez a réteges elrendezés az agyszövet egész felépítésére is jellemző. A rétegen belül egy-egy neuronnak nincs kitüntetett szerepe, hiszen szomszédaitól kevéssé eltérő ingereket kap. A réteg egész felületére jutnak befutó ingerek és a kimenő axonszálak is az egész rétegből erednek. A rétegen belül a neuronokat asszociációs szálak (axonok és dendritek) kapcsolják szorosan össze.
A neuronok egyenkénti leírása helyett vizsgáljuk a réteg r pontja körüli "infinitézimális" tartományba tartozó neuronok átlagos viselkedését. A neuron és memória egyenleteket kis tartományba eső neuronokra átlagolva a neurontér egyenleteit kapjuk. Hasznosnak bizonyult a neuronok aktivitásának jellemzésére bevezetni a küszöb fölé gerjesztett neuronoknak az összes többi neuronhoz való arányát. A legegyszerűbb közelítésben [8, 9] csak gátló és gerjesztő típusú neuronokat különböztetünk meg. Aktivitásukat E(r, t)-, és I(r, t)-vel jelöljük. Ezekre csatolt integro-differenciálegyenletek nyerhetők. Ezen egyenleteket a vizuális kéreg modelljének tekintve sikerült megérteni néhány optikai csalódás fellépését is [8].
Kérdezhetjük, hogy mi történik, ha egy képet [p(rt)] rávetítünk a retinára, ahonnan az a vizuális kéregre tevődik át. Mennyire hű a kérgen megjelenő kép? Az egyenletek megoldása erre ad választ. Lássunk néhány példát, az egyszerű ábrázolhatóság érdekében egy dimenzióban. Egy időben rövid, térben lokalizált fényjelre viszonylag hosszantartó anharmonikus állóhullám gerjesztés jön létre az egyenletek által leírt rétegen. Az állóhullám a gerjesztés helyén marad lokalizálva és mind a gerjesztő, mind a gátló sejteken megfigyelhető. Az állóhullám frekvenciája a felvillanás erősségével arányos és független a térbeli mérettől (7. ábra). A 7. ábrán egy másik jelenség is látható: a kéregben a kontúrok kiemelkednek. Más megoldások ezt a kontúrkiemelést sokkal erőteljesebben mutatják. Közismert, hogy a kontúrok gyenge világítás mellett kevésbé láthatóak. Ezt is reprodukálja a modell (8. ábra).
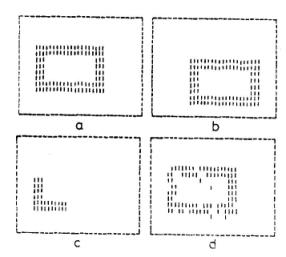
6. ábra. Linearizált hálózat modell [7] alkalmazása ábrák
rekonstruálására egyes részletekből. 510 négyzethálóban elhelyezkedő neuronra a bemenő
ingerként az (a) és (b) ábrán megjelölt sejtekre juttattak jeleket. Több ismétlés után a hálózatban
olyan kapcsolatok alakultak ki, hogy a neuronok közül az egyes ábrákra szintén az (a), (b) ábrákon
megjelölt neuronok válaszoltak megnövekedett aktivitással. Ezek után a hálózatra a (c) bemenő
ingert adva a (d) ábrán megjelölt sejtek váltak aktívvá.
Utolsó példaként nézzük meg, hogyan tükrözi a modell a Fender-Julesz-féle [10] vizuális hiszterézis jelenséget. E jelenség lényege a következő: ha távolból nézünk két reflektort, amelyek egymás mellett vannak, egy fénypontot látunk. A reflektorokat eltávolítva egymástól, bizonyos távolságnál már el tudjuk különíteni a kettőt. Ha ezután ismét közelítjük a reflektorokat, sokkal kisebb köz esetén olvadnak össze egy fényponttá szemünkben, mint előzőleg a távolításkor. Ezt az eléggé speciális jelenséget, ami csak az idegrendszer hatásának tudható be, pontosan megkaphatjuk az egyenletek megoldásával. (9. ábra.)
A statisztikus modellekbe a tanulás is beépíthető a memóriaegyenlet figyelembevételével. Az így kibővített modellben kimutatható az adaptáció a sokat ismételt mintákhoz. Az adaptálódott mintákra a neuronréteg gyengébben, kisebb amplitúdóval reagál, mint az "újakra". Más szerzők [9] hasonló statisztikus modellben, experimentális paramétereket használva, a neuronrétegen az EEG vizsgálatokból is ismert frekvenciájú impulzusok terjedését tapasztalták.
6. Az idegrendszer matematikai analizálásának perspektívái
Az előzőekben leírtuk a neuronhálózat atomjának, a neuronnak egy, a hálózatban betöltött funkciója szempontjából jól közelítő, modelljét. Felírtuk a kölcsönható neuronok hálózatának az egyenleteit. Ezt az egyenletrendszert tekinthetjük a "neuron-gerjesztések" Schrödinger- egyenletének. Innen azonban még hosszú út vezet a rendkívül bonyolult kezdeti feltételekkel rendelkező valódi idegrendszer megértéséhez. Első lépésként a hozzávetőleg homogén kezdeti feltételekkel rendelkező probléma megoldásainak vizsgálatával a hálózat néhány általános tulajdonságát derítjük fel. Az agynak vannak olyan részei, amelyekben nagyobb területre is jónak tekinthető a homogén kezdeti feltétellel való közelítés. Ha az anatómiai ismeretekre támaszkodva [9] adjuk meg a hálózat konstansait, a valódi agy egy területének átlagos aktivitására kapunk modellt. A neuronhálózat lényegi működésének vizsgálatához azonban az idegrendszer strukturálódását feltétlenül figyelembe kell vennünk.
Az élőlényekben a bejövő ingerek feldolgozása és az ezekre adandó válasz kialakulása különböző komplexitású szinteken történik. (10. ábra.) A receptorban és az ahhoz közeli területen sok különböző erősen specializálódott neuront találunk (pl. a béka optikai rendszerében sebességmérő neuronokat). Az idegrendszer központi részére viszont a nagyszámú, de csak néhány fajta neuront tartalmazó rétegek a jellemzőek. Egy-egy ingerre adott válasz annál gyorsabb, mennél alacsonyabb szinten alakult ki (pl. gerincvelői reflexek). Mennél összetettebb egy inger, annál magasabb szinten jön létre a válasz. Az ingerfeldolgozás pályájának magasabb szintre való áttérése sok neuron részvételét, nagyobb időbeli késést eredményez. A sok neuron részvétele több asszociációt tesz lehetővé.
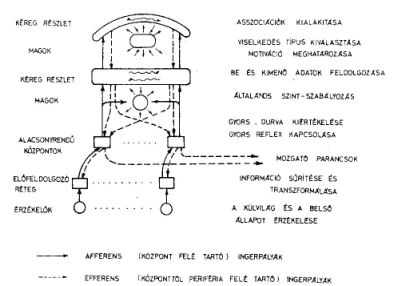
10. ábra. Az idegrendszer feltételezett funkcionális felépítésének vázlata, az egymás fölé
rendelt réteges szerveződés bemutatására
A fentiek szerinti ingerfeldolgozás azonban csak egy lélektelen automata működésének felel meg. A motivációkkal, tudattal bonyolított magasabbrendű idegi működés lényegét valószínűleg a felső agytörzsi magok és az agykéreg kölcsönhatásban kell keresnünk [11, 12]. Míg az idegrendszer aktivitásának túlnyomó része párhuzamos működésként fogható fel, a beszéd és a gondolkodás soros jellegű információ feldolgozáson alapul. Az információ feldolgozásnak ez a váltása a párhuzamos típusúról soros típusúra valószínűleg alapvető szerepet játszik a magasabbrendű idegi tevékenységben.
A fentiek tükrében tekintsük át a matematikai modellezés jelenlegi lehetőségeit. A néhány (≈ 100) neuronból álló hálózatok (egyszerű reflexívek, mesterséges neuron-tenyészetek) vizsgálatára közvetlenül a mikroszkopikus (a neuronokat egyenként számbavevő) leírás alkalmazható. Az így adódó számításoknak a tapasztalattal való egybevetése az alapfeltevések helyességének vizsgálatát, a neuronhálózat paramétereinek meghatározását teszi lehetővé. A nagyon sok neuron átlagos viselkedésének analizálására a statisztikus "neurontér" modell alkalmazható. Így az idegrendszer néhány kollektív tulajdonságának megértéséhez juthatunk közelebb. A sok neuron nem átlagos viselkedésén alapuló tudati jelenségek analizálására olyan modellekre van szükség, amelyekben a fenti megközelítési módok ötvözésén túl, az idegrendszer anatómiai szerkezete is alapvető szerepet kap. Ilyen matematikai modellek kidolgozása a jövő egyik legizgalmasabb kutatási területe.